盾构隧道管片结构设计几个问题的探讨

2019-08-27肖明清王少锋龚彦峰

铁道标准设计 2019年9期

肖明清,王少锋,龚彦峰,唐曌

(1.中铁第四勘察设计院集团有限公司,武汉 430063； 2.水下隧道技术湖北省工程实验室,武汉 430063)

1 概述

盾构法是隧道暗挖施工的一种全机械化施工方法，具有施工安全、掘进速度快、工程质量好、复杂地层适应性强、地表沉降小、对周边环境影响小等诸多优点，已成为隧道工程的主要修建方法之一，在城市地铁、城市铁路、市政道路与基础设施、水下隧道等方面都得到了广泛应用[1]。以地铁为例，截至2017年末，我国内地共计34个城市开通城市轨道交通并投入运营，开通城轨交通线路165条，运营线路长度达到5 033 km，其中70%以上采用盾构法修建。其中，地铁3 884 km，共有62个城市的城轨交通线网规划获批，规划线路总长7 424 km[2]。

随着盾构法隧道应用范围的不断扩大，现有的盾构隧道管片结构设计也出现了一些亟待解决的问题，比如合理的结构计算模型、施工阶段与运营阶段结构安全校核方法、管片配筋优化等。由于国内盾构隧道结构现有计算方法考虑因素不全面、部分计算方法不合理，造成盾构管片配筋量偏大，对管片预制及工程造价都带来了很大影响。基于以上问题提出具体的解决方法，以提高现有盾构隧道结构设计方法的准确性和可靠性。

2 盾构隧道结构计算模型参数取值问题

2.1 隧道常用计算模型

在隧道结构计算模型方面，常用的荷载结构模型有均质圆环模型(修正惯用法采用)、多铰圆环模型、梁-弹簧模型、壳-弹簧模型等[3]，其中，修正惯用法是最常用的方法，但其弯曲刚度有效率η和弯矩提高率ξ参数比较依赖经验取值[4]；多铰圆环模型适用于围岩条件良好且稳定的地层，计算结果偏小，多用于欧洲的隧道结构设计中[5]；梁-弹簧模型可考虑管片接头对管片环刚度折减的影响，并可模拟管片环的错缝拼装效应，但弹簧刚度取值比较复杂[6]；不同于前面的模型默认每环管片都是平面应变状态，壳-弹簧模型可反映管片断面边缘弯曲应力集中的现象，能反映管片的实际受力分布状态[7]，计算参数也更加复杂。

地层结构法理论上适用于各种隧道形状、各种地质条件的分析，但存在使用不太方便、地层计算参数和应力释放率选取困难、锚杆难以准确模拟等方面的问题[8]。荷载结构模型因为计算方法简单，工作量小，具有明确的受力概念及清楚的安全系数评价方法，我国地下铁道及铁路隧道设计规范中均推荐使用[9]。

2.2 梁-弹簧模型计算参数取值

随着大埋深、高水压等复杂地质环境下长大盾构隧道数量的增加，管片结构及接头的力学特性更加受到重视，修正惯用法则无法考虑纵向接头，梁-弹簧模型能够充分考虑纵向接头的位置，并采用旋转弹簧、剪切弹簧和压缩弹簧构成的组合弹簧模拟接头作用，与实际情况最为接近[10]，因此梁-弹簧模型成为盾构隧道设计重要的计算模型。该模型中对应描述接头的3个参数为转动刚度kθ、剪切刚度ks和轴向刚度kn，其中的轴向刚度可通过简单计算得到，常采用无穷大值，转动刚度和剪切刚度多采用接头试验或经验来确定，对于一般的管片接头，提出了用解析求解的方法[11]。由于剪切刚度取值偏小时，主截面的计算弯矩也会偏小，为了安全起见，也常采用将其设定为无穷大的方法，而转动刚度因为受到多种因素影响，其取值比较困难。

管片接头处螺栓的位置决定了管片在承受正负弯矩时刚度不一致；在弯矩作用下，管片接头转动一定角度时接头板分离，其刚度也会发生变化。以上说明了接头转动刚度取值的复杂性，实际情况还要考虑管片主体的形状、接头的形式、螺栓的配置等，这些因素的组合导致接头的种类非常多，为了描述这些管片接头的变形特性，这里采用接头处转角θ与弯矩M呈双线性关系的管片接头模型[12]，如图1所示。

图1 管片接头处转角与弯矩的双线性关系

从图1可以看出，接头弯矩与相对转角呈双线性关系，满足以下公式

(1)

(2)

通过改进的梁-弹簧模型结合接头试验取得相关参数[13-14]，建立稳定可靠的盾构隧道结构分析方法，减少结构计算参数取值的离散性，另一方面，可利用改进的梁-弹簧模型来计算分析修正惯用法中的弯曲刚度有效率η和弯矩提高率ξ[15]。

3 不同阶段安全校核方法问题

在得到隧道结构内力后，需要对结构承载能力和裂缝进行检算，国内主要由两种检算方法：一种是以GB50010—2010《混凝土结构设计规范》为代表的按照极限状态法进行截面承载能力和正常使用极限状态下裂缝宽度检算的方法；一种是以TB10003—2016《铁路隧道设计规范》为代表的按照破损阶段法和容许应力法进行截面抗压强度和抗拉强度检算的方法[16]。

现行TB10003—2016《铁路隧道设计规范》中使用破损阶段法检算钢筋混凝土构件截面强度时，根据结构所受的不同荷载组合和不同的破坏原因，在计算中分别选用不同的安全系数，按所采用的施工方法检算施工阶段强度时，安全系数可采用表列“主要荷载+附加荷载”栏内数值乘以折减系数0.9[17]。以上说明破损阶段法中对施工阶段的隧道结构检算进行了安全系数的折减。

对于盾构法隧道结构，采用极限状态法进行结构检算时，需检算结构承载能力、最大裂缝宽度和衬砌环变形。大量的现场实测资料表明，管片结构内力一般远小于设计值，对于黏性土地层，运营阶段一般采用水土分算，施工阶段采用水土合算，因而施工阶段为控制工况，采用水土合算进行结构计算造成了盾构隧道结构配筋量偏大。与设计使用年限相比，在结构施工过程中所出现工况的持续性很短，应当按照短暂设计工况考虑，适当降低安全系数或减小分项系数是有必要的。

采用极限状态法进行盾构隧道设计时，考虑施工阶段为短暂设计工况，仅进行强度和变形验算；运营阶段为持久设计工况，进行强度、裂缝和变形验算，按TB10003—2016《铁路隧道设计规范》安全系数进行验算，用施工期荷载组合和运营期荷载组合分别进行结构的检算，得出最终配筋，可以达到减少配筋的目的。

4 盾构管片配筋优化设计

盾构隧道管片配筋优化设计是在确保隧道结构安全的前提下合理的优化设计参数，充分利用材料的性能，使管片中混凝土与钢筋受力协调一致，达到节省材料、降低工程成本的目的。

4.1 纤维梁单元模型

管片结构设计在截面内力计算时，钢筋和混凝土一般采用统一的结构等效刚度，忽略了钢筋分布对所在截面结构刚度的影响，导致配筋结果多数偏于保守。

通过有限元方法，建立了可描述钢筋与混凝土共同作用的纤维梁单元模型，利用数值积分方法，可精确地计算出钢筋混凝土的等效刚度值。在管片配筋校核分析时可充分考虑钢筋的空间分布，从而较为准确地模拟钢筋量对管片内力值的影响，实现管片配筋的优化[18]。

钢筋混凝土模型示意如图2所示，模型将管片划分成细网格，再对网格中的每一小块根据公式(3)进行积分，求出截面的刚度。

图2 管片钢筋混凝土模型

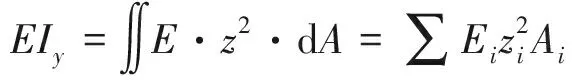
(3)

式中，EIy为Y轴抗弯刚度；z为所积分单元格到Y轴的距离；Ai为所积分单元格面积。

由此可以看出，根据是否有钢筋，钢筋混凝土材料弹性模量E在不同截面处的取值不同，主要是依据该点的应力应变状态而定，通过该模型可对配筋优化后的钢筋用量及分布结果进行校核。

4.2 管片配筋优化设计

大量的盾构隧道结构配筋计算表明，影响配筋量的因素包括设计方法、水土压力计算方式、施工注浆荷载、地层与管片结构相互作用方式、钢筋分布形式等。

(1)设计方法

在设计方法上，采用JTG D70—2—2014《公路隧道设计规范》中的容许应力法和破损阶段法进行设计通常要比按照GB 50010—2010《混凝土结构设计规范》中的极限状态法进行设计得到的配筋量要大，在盾构隧道设计中，需要根据不同工况进行比较，选择合理配筋结果。另外，根据第3节考虑施工阶段为短暂设计工况，运营阶段为持久设计工况，则设计更为合理。

(2)水土压力计算方式

在水土压力计算方式上，全部水土合算得到结构内力最大，水土分算最小，目前对水土压力统一进行水土合算或分算的做法不尽合理，可以根据实际情况分土层进行相应的水土合算或分算，可一定程度减少配筋量。

(3)施工注浆荷载

结构内力计算时，考虑注浆荷载会使管片配筋量降低，均匀注浆比非均匀注浆配筋量更少，因此，注浆荷载对结构荷载效应来说是有利荷载，在管片结构分析及配筋计算中应考虑注浆荷载的影响。

(4)地层与管片结构相互作用方式

地层与管片结构的相互作用通常采用地基反力或者地层弹簧来模拟，通过设置地基抗力、单一地层弹簧以及多个地层弹簧3种工况进行比较分析，结果表明：其最终配筋量依次递减，但总体相差不大，可根据需要设置地基反力或地层弹簧。

(5)钢筋分布形式

钢筋分布形式同样对管片配筋量产生影响，考虑错缝拼装时弯矩沿幅宽呈不均匀分布[19-20]，为充分提高钢筋材料的利用效率，管片不采用均匀配筋。根据结构计算得到断面内力作为平均内力，幅宽两侧各0.15B(B为幅宽)范围内调整弯矩为平均弯矩的115%，幅宽中间0.7B范围内调整弯矩为平均弯矩的93.6%，根据调整后的内力大小进行配筋。

4.3 管片配筋优化算例

某地铁盾构隧道的外直径为6.2 m，内直径为5.5 m，管片幅宽取1.5 m。管片采用6块分割，采用错缝拼装，混凝土强度等级C50，顶部螺栓偏角β为18.00°。隧道位于复合地层，埋深取29.3 m，地下水位线为-4 m，其地质参数取值见表1。

表1 某地铁盾构隧道地质参数

管片配筋计算参数见表2。

表2 管片配筋计算参数

方案1，管片配筋按照破损阶段法设计，计算采用修正惯用法计算模型，弯曲刚度有效率η取0.75，弯矩提高率ξ取0.3，地层反力采用地层弹簧模拟，统一采用水土分算，按施工阶段和运营阶段的最不利工况计算，进行对称配筋。方案2，配筋优化按照极限状态法设计，采用改进梁-弹簧模型，分土层进行水土合算或分算，考虑施工阶段为短暂设计工况，不进行裂缝宽度验算，运营阶段为持久设计工况，并利用纤维梁有限元模型对不同受力阶段进行验算，两种方案的配筋结果见表3。

表3 两种配筋方案的配筋结果

从表3可以看出，配筋优化后，方案2的管片钢筋用量减少约41%。其中，设计方法、计算模型、水土压力计算方式对管片的配筋结果影响较为明显，极限状态法对施工阶段和运营阶段进行不同的安全校核影响最大。

铁四院在盾构隧道设计方面积累了大量的研究成果和丰富经验，在此基础上与上海同岩科技土木工程有限公司合作开发了盾构隧道管片结构计算与配筋软件V1.0，该软件是基于同济曙光三维数值分析平台并依据现行规范开发的盾构隧道专业设计分析软件，采用修正惯用法或梁-弹簧模型对衬砌结构进行三维内力变形分析、管片配筋、管片验算、接头刚度计算、接头强度校核、地震响应分析、抗浮验算，并可实现对盾构隧道同一横断面不同工况、不同阶段、不同分析模型的管片计算分析，自动生成分析报告等。该软件可应用于城市地铁、城市铁路与道路、市政设施、水利水电等各类型盾构隧道管片结构计算和配筋设计。