多普勒盲区条件下的交互式多模型粒子滤波算法

韩 伟 何成伟 朱 沛

(空军预警学院 武汉 430019)

0 引言

机载预警雷达采用了脉冲多普勒(PD)体制，且处于下视工作，具有良好的低空探测性能，但其面临着比地基雷达更为严重的地(海)杂波影响，这些杂波分布范围广、强度大[1]。同时，机载预警雷达主瓣杂波谱展宽程度较地基雷达也要严重得多，在频域中造成的遮挡效应也更为严重，从而形成了固有的多普勒盲区问题[2-5]，当目标径向速度落入该盲区时，目标无法被检测，从而造成航迹连续丢点，引起目标航迹暂消、重新起批甚至断批的现象。多普勒盲区的存在，降低了雷达情报的质量，增加了雷达情报分析的难度。因此，开展多普勒盲区条件下的机载预警雷达目标跟踪技术的研究，具有十分重要的应用价值。

多普勒盲区条件下的目标跟踪实际上是带有状态空间约束条件的目标状态估计问题[6-7]。目前，针对此类问题的研究较少。Neil Gordon等人最早采用改进的盲区粒子滤波算法(Blind Doppler Particle Filter, BDPF)来跟踪多普勒盲区条件下的空中目标[8]，该方法将多普勒盲区限制的先验信息并入到粒子滤波算法中，对匀速运动(CV)目标具有较好的跟踪效果。针对多普勒盲区条件下的机动目标跟踪问题，一些学者提出了基于交互式多模型的粒子滤波算法[9]，该方法将匀速模型和匀加速度模型结合起来处理盲区外目标的机动，然而，目标的实际运动模型是未知的，多模型的选择较为困难，基于此，一些学者提出了基于当前统计模型的盲区粒子滤波算法(CS-BDPF)[10]和基于差分机动检测的粒子滤波算法[11]，均取得了较好的跟踪效果。但以上研究中，均将盲区内的目标运动模型假定为仅做无过程噪声的匀速运动。这样，当目标在进入多普勒盲区时，即使发生较小机动，以上算法也会产生较大的目标状态估计误差。因此，算法具有一定的局限性。

另外，W.Koch和J.M.C.Clark等人在机载GMTI雷达探测地面运动目标背景下，采用高斯和滤波(GSF)方法实现多普勒盲区条件下的地面目标跟踪[12-14]，获得了较好的跟踪性能。另外，一些学者将多模型应用到地面“走-停-走”目标的跟踪上[15-17]，该方法将目标落入盲区时“停”的状态作为一个增加的运动模型，从而在多模型的基础上实现了多普勒盲区条件下的地面目标跟踪。以上研究都是在GMTI雷达对地面观测的背景下展开的，由于地面目标与空中目标的运动特性存在较大差异，且GMTI雷达与机载预警雷达工作模式也不尽相同，因此，以上算法模型都不能适用于多普勒盲区条件下，机载预警雷达对空中目标的跟踪问题。

基于以上分析， 本文以机载预警雷达对空中目标的探测为背景，着重针多普勒盲区条件下的机动空中目标跟踪问题开展研究，提出了一种基于交互式多模型的盲区粒子滤波算法(Interacting Multiple Model-Blind Doppler Particle Filter, IMM-BDPF)来处理多普勒盲区内的目标跟踪问题，获得了较好的目标跟踪性能。

1 多普勒盲区问题分析

系统的状态方程与观测方程分别为

x(k+1)=f(x(k),m(k))+Γ(k,m(k))w(k,m(k))，k=1,2,…

(1)

z(k+1)=h(x(k+1),m(k))+n(k+1)，
k=1,2,…

(2)

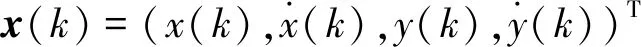
pij=p{m(k+1)=j|m(k)=i}，i,j∈Ω

(3)

多普勒盲区对目标状态的限制可表示为

(4)

(5)

2 基于交互式多模型的多普勒盲区粒子滤波算法

2.1 IMM-PF算法

IMM-PF在解决非线性、非高斯系统的机动目标跟踪问题上能够获得更好的目标状态估计效果[18]。算法在每一个循环包括四个步骤：输入交互、滤波、模型概率更新和输出交互。与基于IMM的卡尔曼滤波算法中对各模型状态估计值进行输入交互不同，IMM-PF算法是将各模型产生的粒子进行输入交互，然后进行粒子滤波和状态的输出交互。但由于各模型在完成粒子滤波过程中，大量的粒子要传递到下一时刻，如果在所有粒子之间都进行交互运算，计算量会很大。因此，可采用每个粒子与其它模型的估计值进行交互运算[18]。这样既能反映出其它各个模型对该粒子的影响程度，解决不同类型滤波器带来的交互问题，同时可以适当减小计算量。

IMM-PF算法的具体步骤可表示如下[18]：

步骤1：输入交互

模型间的混合概率表示为

μi|j(k-1|k-1)=pijμi(k-1)/cj，i,j=1,2,…,M

(6)

(7)

式(7)中，N为各模型的粒子数。

步骤2：滤波

粒子预测过程表示为

(8)

预测输出表示为

(9)

残差表示为

(10)

粒子权重计算表示为

(11)

式(11)中，R(k)为噪声n(k)的协方差。对粒子权重进行归一化得到

(12)

状态估计表示为

(13)

协方差估计表示为

(14)

步骤3：模型概率更新

预测输出的均值表示为

(15)

残差协方差表示为

(16)

模型j的似然函数为

(17)

各模型的更新概率可表示为

(18)

步骤4：交互输出

(19)

2.2 IMM-BDPF算法

在目标跟踪过程中，各种因素的影响会使得雷达无法获得目标的量测值，此时仅能根据目标运动状态和前一时刻的状态估计值进行预测得到当前时刻的状态估计值。这里，我们将雷达无量测值的原因归结为两类：

1)目标RCS起伏等因素决定的目标检测概率Pd<1；

2)目标绝对速度的减小或相对视线角的改变而进入多普勒盲区。

IMM-BDPF算法过程如下：

步骤1：输入交互

当k-1时刻无量测值，且判断为多普勒盲区所引起时，则进行多普勒盲区条件下的交互运算，得到各模型的混合输入盲区粒子，可表示为

(20)

其余部分同IMM-PF算法。

步骤2：滤波

1)有量测值情况

当k时刻有量测值时，算法同IMM-PF。

2)无量测值情况

(21)

(22)

且式(22)得到的预测值需满足约束条件：

(23)

步骤3：模型概率更新

当k时刻有量测值时，则同IMM-PF算法；当k时刻无量测值时，则模型的概率更新为

(24)

步骤4：交互输出

根据前面计算的结果，目标状态的最终估计值可表示为

(25)

式(25)中，δ(k)为Kronecker delta函数，当目标进入多普勒盲区，δ(k)=1；当目标在多普勒盲区外，δ(k)=0。

2.3 丢点原因判断方法

正如2.2中所述，目标丢点主要由Pd<1和多普勒盲区两种原因造成，IMM-BDPF算法中需要对两种原因进行判断，具体的判断过程如下：

步骤2：由于目标进入多普勒盲区前，其径向速度有逐渐减小的趋势，并且在进入盲区的前一时刻，径向速度在最小可检测速度的边缘。因此，在完成步骤1的判断后，还需进行两个条件的判断，即

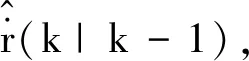
3 仿真实验及结果分析

地面目标一般通过“停”的方式进入多普勒盲区，从而逃避GMTI雷达的检测，与之不同的是，空中目标主要通过有意或无意地改变相对雷达视线进入多普勒盲区，因此，采用CV模型和CT模型可以较好的描述目标在多普勒盲区条件下的运动特性。对于其它高机动模型，如Singer，jerk等，由于加速度变化率较大，经历的多普勒盲区时间一般较短，故不予考虑。因此，目标的模型集可以包括一个CV模型和两个CT模型(顺时针方向转弯和逆时针方向转弯)。模型转移矩阵为

(26)

图1表示目标运动轨迹及多普勒盲区分布，目标在运动过程中经历了3个多普勒盲区，3个多普勒盲区内目标分别丢失11个点迹、7个点迹和13个点迹，其中第1个盲区和第3个盲区发生在匀速运动过程中，第2个盲区发生在恒速转弯运动过程中。图2表示算法的滤波结果及新出现量测值时刻粒子云波门的分布，在多普勒盲区的状态约束下，新出现的量测值均可落在某个模型形成的粒子云内，形成与原航迹的正确关联。

图1 目标运动轨迹及多普勒盲区分布

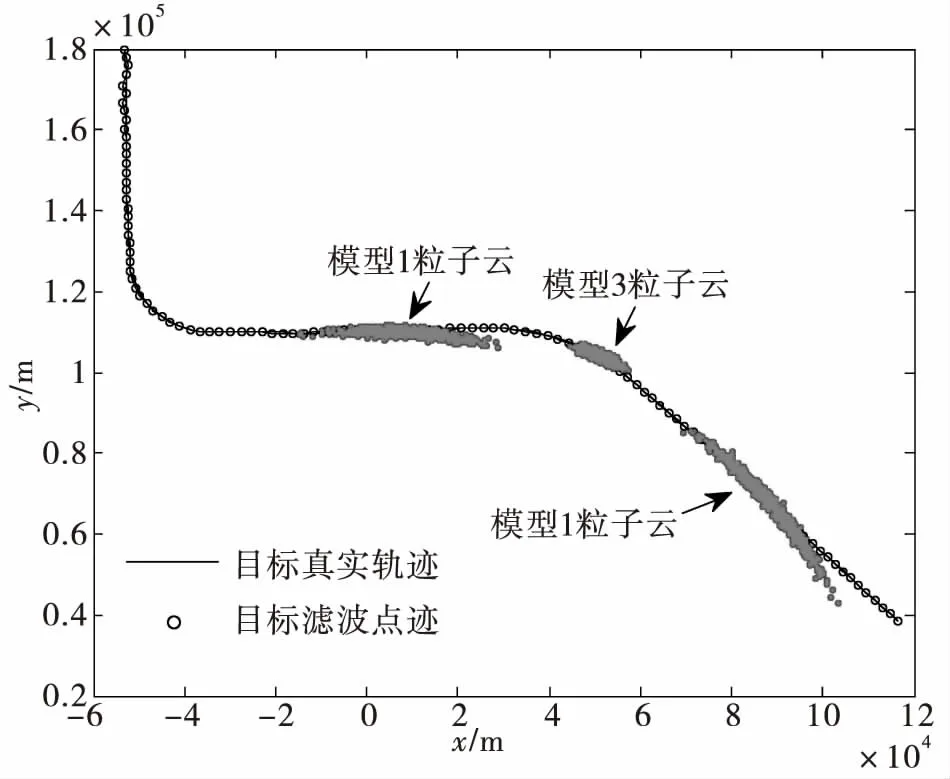
图2 算法的滤波结果及粒子云分布

图3表示三种运动模型概率的变化情况，在3个盲区时段，由于连续多个采样时刻点迹丢失，主模型(概率最大的运动模型)概率连续下降，其它模型概率增加。在200次蒙特卡洛仿真条件下，对IMM-BDPF算法和IMM-EKF(在丢点时刻，按照Pd<1的情况进行预测)算法的滤波性能进行比较，两种算法在x方向上的位置滤波均方误差RMSEpx如图4所示。从仿真结果中可以看到，在多普勒盲区之外，两种算法的滤波误差基本相同，而在多普勒盲区，由于无量测值的更新，两种算法的滤波误差逐渐增加，但IMM-BDPF算法在所有模型条件下的预测过程中加入了多普勒盲区的状态约束，滤波精度要高于IMM-EKF算法。

图3 三种模型的概率

图4 滤波误差

从以上分析可知， IMM-BDPF算法的目标跟踪性能要优于IMM-EKF算法，但该算法最大的优势在于跟踪多普勒盲区内运动状态发生了改变的目标。这里，我们设置第二种飞行场景，即目标的初始状态为x(0)=(-57km,0m/s,200km,-220m/s)T，目标的运动过程和其它仿真参数同上。目标运动轨迹及多普勒盲区分布如图5所示，目标在运动过程中经历了两个多普勒盲区，两个盲区内目标分别丢失17个点迹和10个点迹，在第1个盲区中，目标运动模型发生了改变，即由匀速运动转换到恒速转弯运动。从图6所示的滤波结果及粒子云波门分布可以看到，该算法能对此类运动场景的目标进行有效的跟踪。

图5 目标运动轨迹及多普勒盲区分布

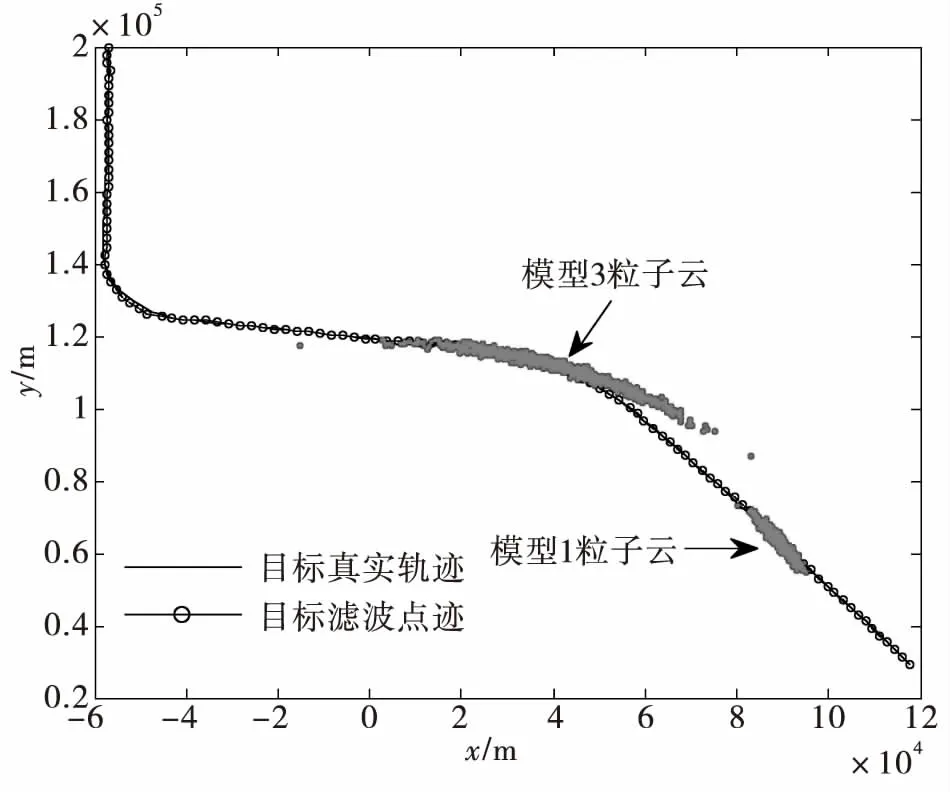
图6 算法的滤波结果及粒子云分布

图7表示3种运动模型概率的变化情况，在点迹丢失时刻，主模型的概率下降，其它模型概率增加，这对盲区内目标发生机动的情况有利。在200次蒙特卡洛仿真条件下，两种算法的RMSEpx如图8所示。从仿真结果可以看到， IMM-BDPF算法在盲区内的滤波精度要明显高于IMM-EKF算法。

图7 三种模型的概率

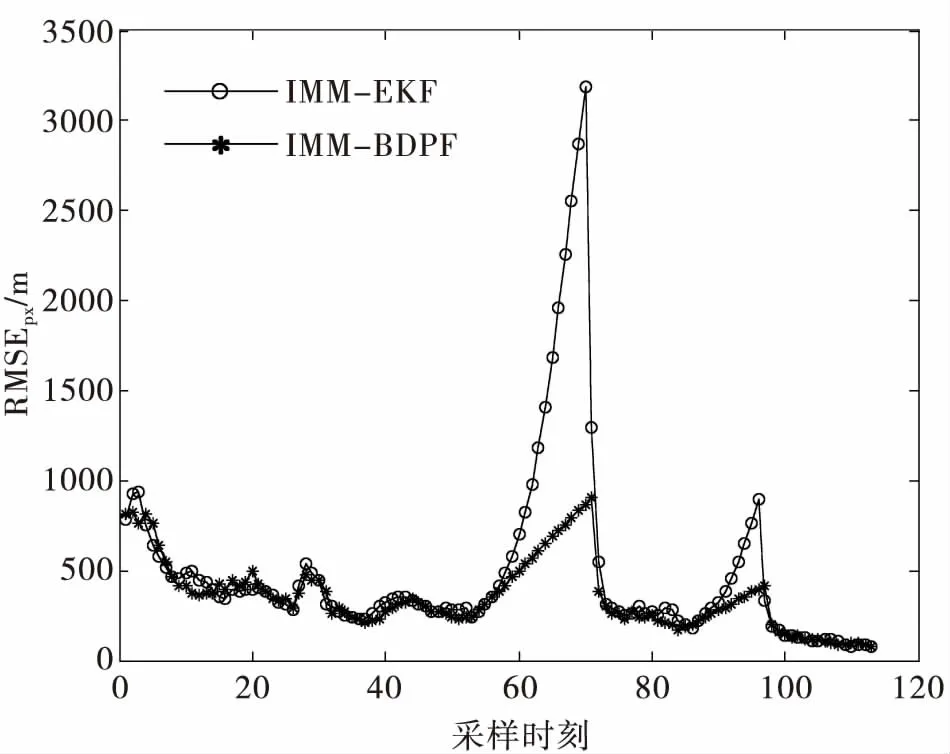
图8 滤波误差

4 结束语

本文在机载预警雷达对空模式背景下，针对多普勒盲区造成的航迹不连续问题，提出了一种IMM-BDPF算法对目标进行跟踪，该算法充分利用多普勒盲区的先验信息，结合目标机动常用模型集，对IMM-PF算法进行了改进。仿真结果表明，对于多普勒盲区条件下做机动的目标，本文提出的IMM-BDPF算法具有较好的跟踪效果，尤其目标在盲区内做机动时，该算法能够获得较高的目标状态估计精度。