一道高考试题的解法探究与变式拓展

李海堂

(重庆市荣昌中学校 402460)

众所周知，教学离不开解题，高考真题可以为教师的授课提供有益的、切实可行的案例，有利于学生对数学知识的理解和思维的发展. 近年来，同角三角函数的基本关系、三角恒等变换、三角函数的最值问题一直是高考的热点问题，此类问题综合性强、内涵丰富，解法多样. 本文对2018年高考全国Ⅰ卷数学理科16题进行解法探究及变式拓展.

一、试题呈现

已知函数f(x)=2sinx+sin2x，则f(x)的最小值是____.

二、解法探究

1.利用四元均值不等式，巧妙转化

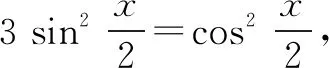
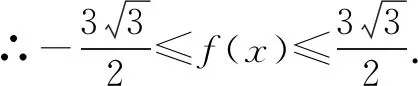
解法2 由已知得：f(x)=2sinx+sin2x=2sinx(1+cosx)

∴[f(x)]2=4sin2x(1+cosx)2

=4(1-cosx)(1+cosx)3

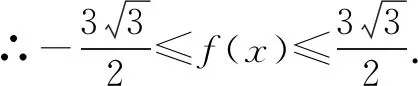
点评运用的是四元均值不等式解决此题，它的突破口是通过二倍角公式转化为同一个角三角函数，平方后通过四元均值不等式“一正、二定、三取等”求最值，平方变换是关键，凑成和是一个常数是难点，四元均值不等式由于平时训练较少，学生难以突破.

2.利用导函数法，直击要害

解法3由已知得：

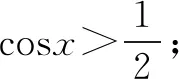
又f(x)=2sinx+sin2x=2sinx(1+cosx),

解法4由已知得：f(x)=2sinx+sin2x=2sinx(1+cosx),

∴[f(x)]2=4sin2x(1+cosx)2=4(1-cosx)(1+cosx)3.

令t=cosx，则g(t)=4(1-t)(1+t)3(-1≤t≤1)

g′(t)=4[-(1+t)3+3(1-t)(1+t)2]=4(1+t)2(2-4t).

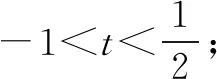
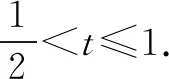
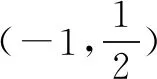
点评通过对f(x)求导或[f(x)]2后换元再求导，确定其单调性，根据单调性求出f(x)的最值，关键点是函数求导，解法4平方转化利用sin2x+cos2x=1换成一个未知数cosx的函数是难点，求导方法学生容易想到，但容易出错.

3.利用几何方法，凸显本质

解法5由已知得：

f(x)=2sinx+sin2x=2sinx(1+cosx).

设sinx=m，1+cosx=n，则m2+(n-1)2=1，f(x)=2mn.

问题转化为在m2+(n-1)2=1下，求2mn的最小值.

当m=0时，f(x)=0.

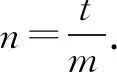
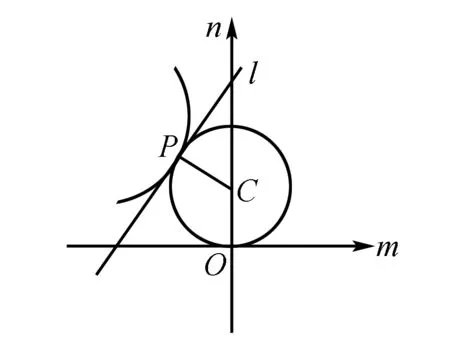
求f(x)的最小值只需考虑t<0的情况.

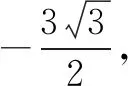
解法6 由已知得：f(x)=2sinx+sin2x=2sinx(1+cosx).

设sinx=m，1+cosx=n，则m2+(n-1)2=1，f(x)=2mn.

问题转化为在m2+(n-1)2=1下，求2mn的最小值.

当m=0时，f(x)=0.

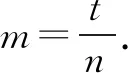
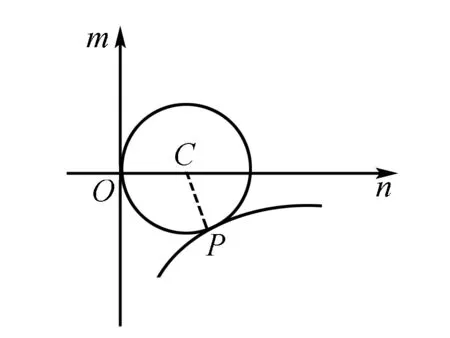
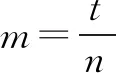
令f(n)=-n4+2n3(0≤n≤2),

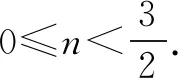
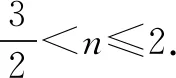
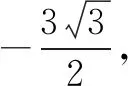
点评把三角问题通过换元转化为几何问题，采用双换元的思想，通过三角变换消去sinx、cosx，利用数形结合的思想，研究两曲线的切线问题求得其最小值，对考生的化归与转化、运算求解的能力要求较高.

三、变式拓展

通过对问题进行拓展研究，给出如下变式.

变式1已知函数f(x)=2sinx+cos2x，则f(x)的最小值是____.

解由f(x)=2sinx+cos2x得

当sinx=-1时，f(x)取得最小值，最小值为-3.

变式2已知函数f(x)=2sin2x+sin2x，则f(x)的最小值是____.

解由f(x)=2sin2x+sin2x得

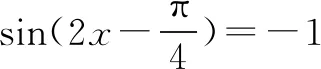
变式3已知函数f(x)=2sinx+2cosx+sin2x，则f(x)的最小值是____.

解法1由f(x)=2sinx+2cosx+sin2x得

故当t=-1时，y最小即f(x)取得最小值，最小值为-2.

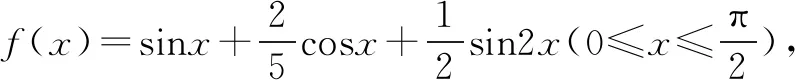
∴g′(t)

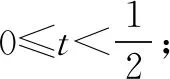
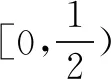
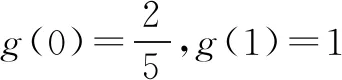
如果学生在平时的练习中能总结这些题型的方法，三角函数求最值问题就很容易得到解决.

(1)形如y=asin2x+bsinx+c的三角函数，可先设t=sinx，转化为关于t的二次函数求最值问题.

(2)形如y=asinx+bcosx+c的三角函数，可转化为y=Asin(ωx+φ)+k的形式，再求最值.

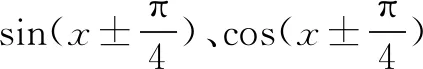
当然，有些三角函数求最值的题目难度较大，要利用三角恒等变换、换元思想通过均值不等式或用导函数求最值，这种题目换元化简及求导都较复杂，易出错，找导函数的零点是一个难点，运算能力要求也较高.