对高考中一类函数最值问题的思考
2019-08-26田保
数理化解题研究 2019年22期
田 保
(安徽省铜陵市第一中学 244000)
函数最值是高考中的热点,常与导数,三角函数,方程等知识点联系起来,解题方法有均值不等式,换元法,数行结合法等,具体题目应该结合已知条件 灵活选用合适的解题方法.下面看一道最值问题的不同解法.


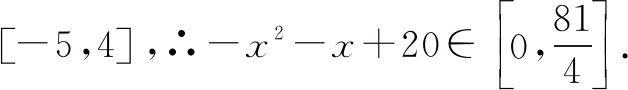




∴-3≤z≤3,∴0≤z2≤9.




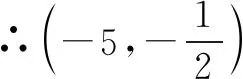

在x=4或5处取得最小值,
∴ymin=3.

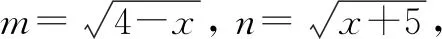
则b=(m,n)的终点表示圆心在原点,半径为3的圆在第一 象限上.

2019-08-26田保
田 保
(安徽省铜陵市第一中学 244000)
函数最值是高考中的热点,常与导数,三角函数,方程等知识点联系起来,解题方法有均值不等式,换元法,数行结合法等,具体题目应该结合已知条件 灵活选用合适的解题方法.下面看一道最值问题的不同解法.


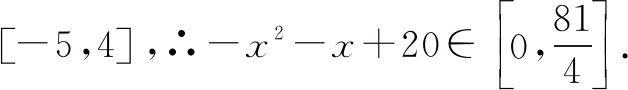




∴-3≤z≤3,∴0≤z2≤9.




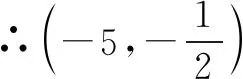

在x=4或5处取得最小值,
∴ymin=3.

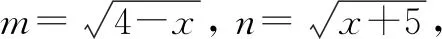
则b=(m,n)的终点表示圆心在原点,半径为3的圆在第一 象限上.
