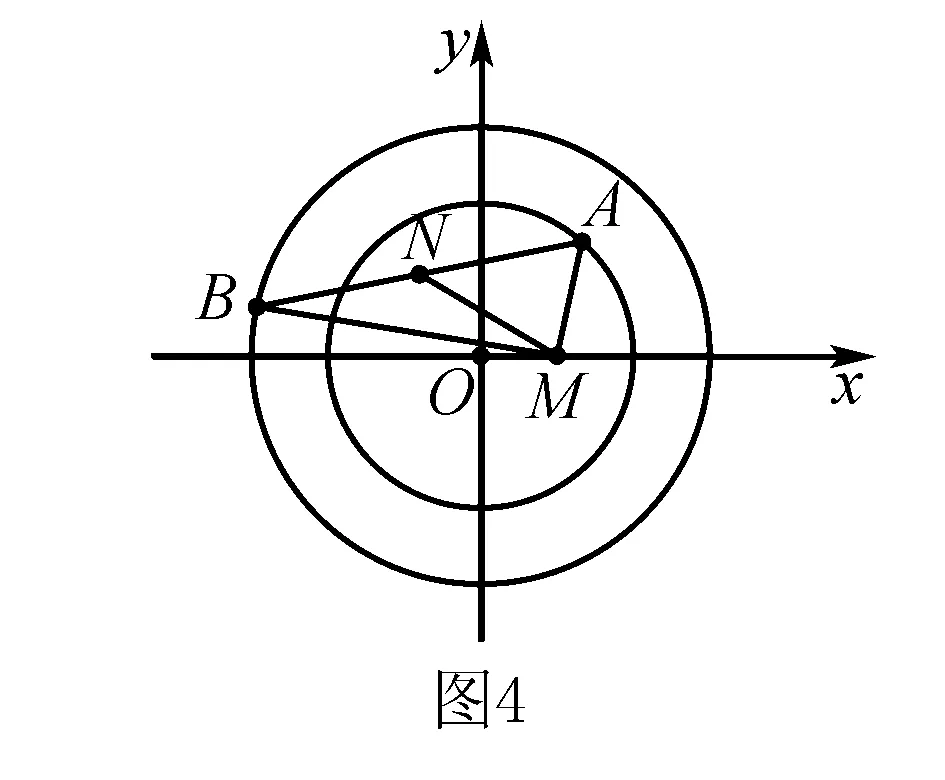
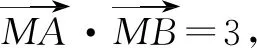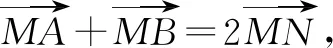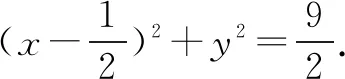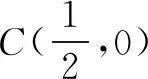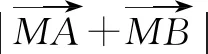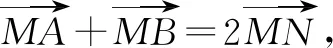向量解题策略之“无中生有”
2019-08-26雷亚庆
数理化解题研究 2019年22期
雷亚庆
(江苏省南京市大厂高级中学 210044)
一、无中生“三角形”
例1(2010浙江理数)已知平面向量a,b(a≠0,a≠b)满足|b|=1,且a与b-a的夹角为120°,则|a|的取值范围是____.
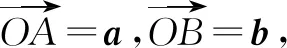
问题转化为:△OAB中,已知OB=1,∠OAB=60°,求边OA长的取值范围.
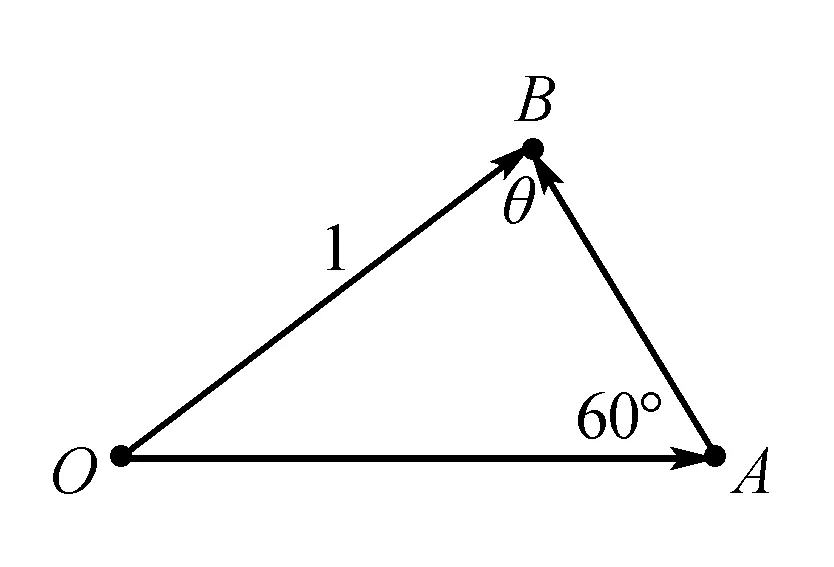
图1
设∠OBA=θ(0°<θ<120°),
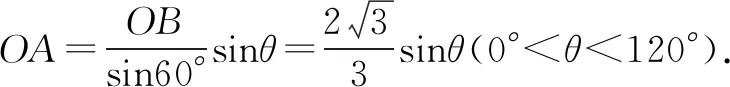
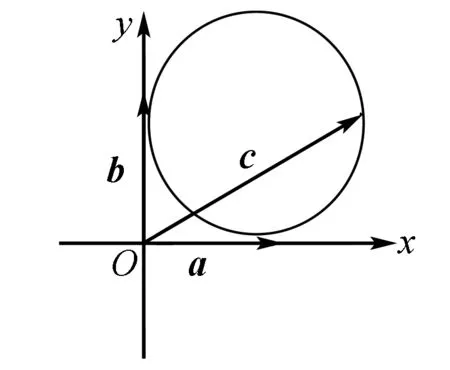
因为0°<θ<120°,所以0 反思根据向量减法的几何意义将题设条件表示在三角形中,利用解三角形即可迎刃而解. 例2(2013年高考湖南卷(理))已知a,b是单位向量,a·b=0.若向量c满足|c-a-b|=1,则|c|的取值范围是( ). 图2 解析如图2,将a,b移至同起点O,因为a·b=0,所以有a⊥b.以O为起点,以表示a,b的两条有向线段所在直线为x,y轴建立平面直角坐标系. ∵a,b是单位向量,∴a=(1,0),b=(0,1). 设c=(x,y)则c-a-b=(x-1,y-1). 由|c-a-b|=1可得:(x-1)2+(y-1)2=1. 即答案为A. 反思本题首先利用坐标法将向量问题转化为代数问题,再利用几何意义转化为求圆上一点到原点的距离的最大最小问题,从而使问题顺利解决. 图3 (x1-1)(x2-1)+y1y2=3③. ①+②+③×2得:(x1+x2)2-2(x1+x2)+(y1+y2)2+2=19,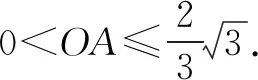
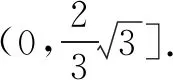
二、无中生“圆”

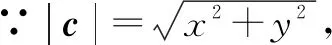
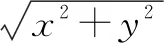
三、无中生“平行四边形”

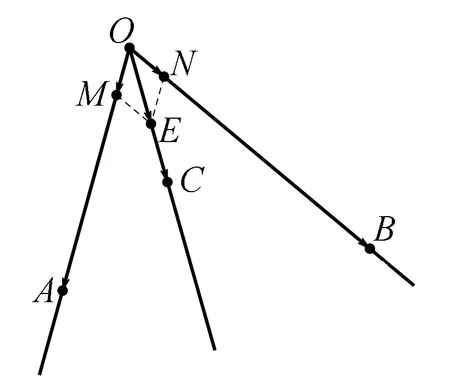
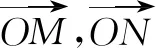

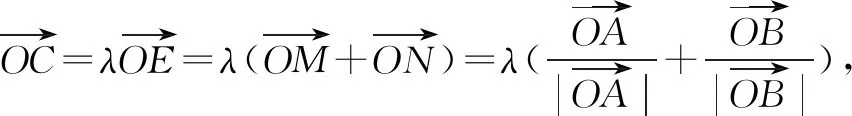
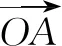
四、无中生“中线”