平面向量在高中数学中的代数和几何运用

何正文

(广东省肇庆市百花中学 526000)

一、代数角度的运用

分析从题目的已知与结论分析.条件向量的起点都是O点，而所求向量模的比值都是A点为起点，于是将条件中的起点O全部转化为点A即可，解析如下：

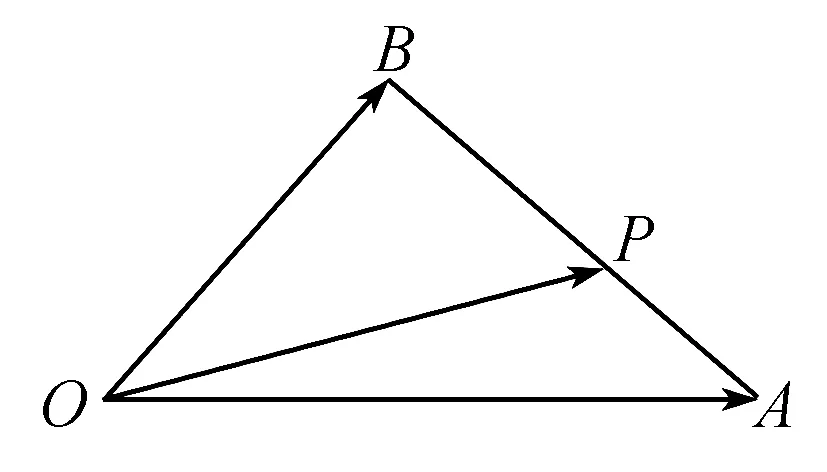
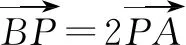
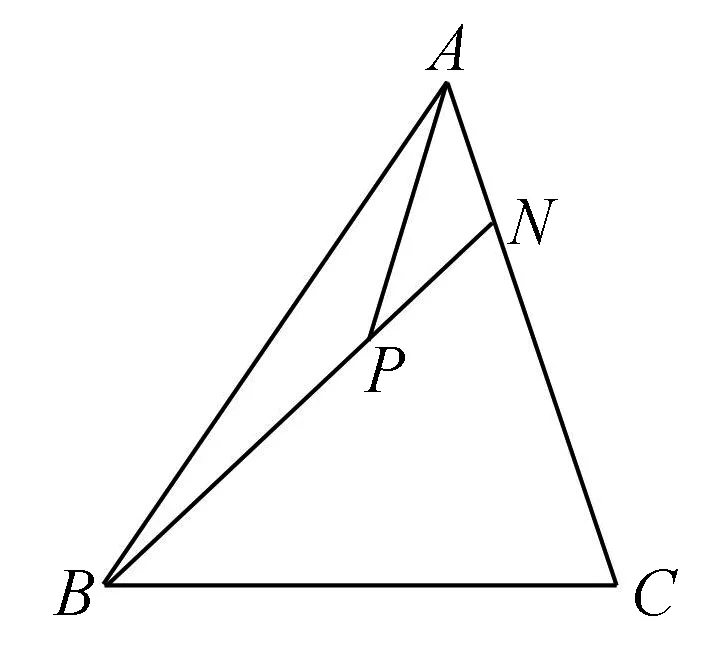
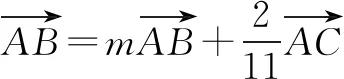
从代数角度解决平面向量综合题目，主要展示了运算的能力，关键是寻找已知向量与未知向量间的转化，主要是看向量的起点、终点，然后通过回路法，形成与条件结论有关的回路.借助代数运算解决平面向量综合题目，是解决形如平面向量综合题目的一般性方法.

二、几何角度的运用

例5已知a，b是平面内两个互相垂直的单位向量，若向量c满足(a-c)·(b-c)=0,则|c|的最大值是____.

∴c对应的点C在圆x2+y2=2上即可.

从几何角度解决平面向量综合题目，展示了“形”的魅力，从中可以感受到以形解数的优势.关键是利用回路法将条件与结论联系起来，有的时候需要借助平面几何知识，这样会大大地简化运算.

三、代数、几何角度综合运用

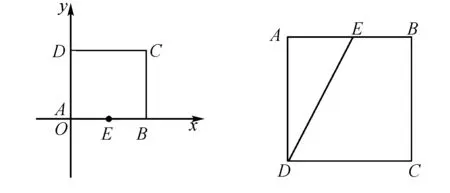
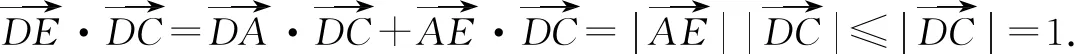
在高中数学课程中进行向量教学适应了当代高中数学课程发展的趋势，不仅必要而且可行，具有非常重要的意义；向量知识既符合学生发展的需要，又符合学生学习的认知特点；高中进行向量教学的意义主要有：能优化学生的认知结构，提高学习质量，增强学习效益，能培养学生的思维品质，发展学生的思维能力，能培养学生的建模能力，有利于学生全面、和谐发展，能培养数学的审美能力，了解数学文化的发展.