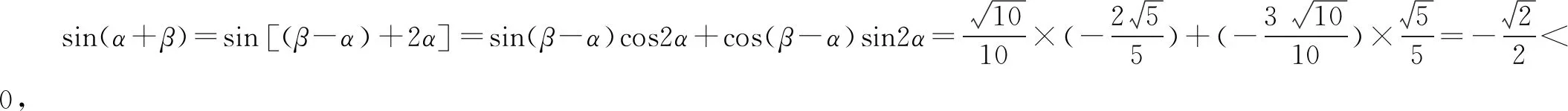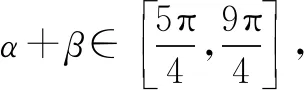三角函数中确定角范围的几种方法

吴志鹏

(福建省德化第一中学 362500)

三角函数中的求值问题、求角问题，经常会与角的范围“相遇”，学生在解题过程中也经常会因判断不出角的范围而导致解题失误，本文介绍确定角范围的几类方法，供读者参考.

一、估值限界，确定角的范围

通过估算题目所给的函数值，并与特殊的三角函数值作对比，对角的边界作限制，这样就能比较准确地估计出角的范围，判断三角函数值和符号.

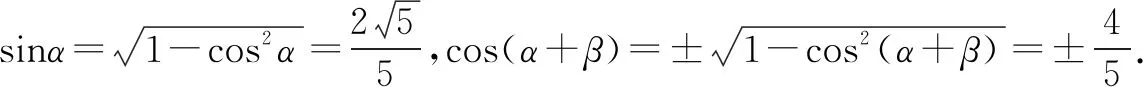
∵α,β均为锐角，∴0<α+β<π，由于角的范围太大而判断不出cos(α+β)的符号．

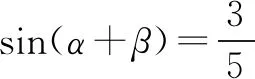
二、单调比较，确定角的范围

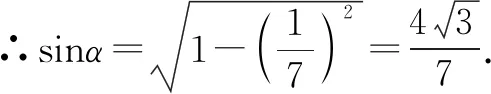
三、赋名求值，确定角的范围

利用不同限象角三角函数值的符号不同这一差异，可通过给角赋名，并求值，利用值的符号来判断角的范围，如第一、二象限角可赋“余弦”名加以区分，因为这两个象限角的余弦值异号；若赋与“正弦”名，则这两个象限角正弦值符号相同区分不出角的范围.

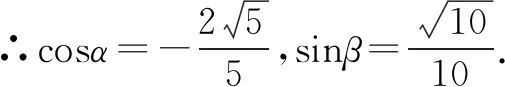
又α+β∈(π,2π)，

四、研究倍角范围，确定角的范围

如给定角α的范围，则2α的范围比α的范围，伸长到两倍，角也相应地扩大了，但通过对其倍角的三角函数值的符号及其对应角范围的研究，则能有效将倍角的范围缩小，进而达到缩小角的目的.

五、同角异名求值，确定角的范围

对于一些范围比较大的角，通过一次赋名求值，仍然确定不了范围，则可通过第二次赋与其不同的函数名，进行同角异名求值获取符号，并研究两次角的范围取其公共范围.