基于COSMO-RS的单工质气液相平衡热物性计算方法

(上海理工大学能源与动力工程学院 上海200093)

由于环境因素的限制，制冷系统中对制冷剂的要求越来越高[1]，越来越多的专家学者投入到新型制冷剂的研发中。气液相平衡数据对于制冷剂的工程应用和设计意义重大，是热力学中不可或缺的组成部分。气液相平衡数据主要可以通过状态方程法、活度系数法计算及模拟仿真和实验测定。吴献忠等[2]利用UNIFAC基团贡献法预测了混合制冷剂R32+R227ea、R227ea+R134a和R152a+R227ea及三元混合制冷剂R32+R125+R134a的气液相平衡数据。宋有强等[3]采用PR状态方程及其混合法则计算了混合制冷剂CO2+R600的气液相平衡数据。董学强等[4]利用基于循环法的高精度可视化中低温相平衡装置测量了温度为255、265、275、288 K时R134a/R290的气液相平衡数据。状态方程法计算严格，但参数多，应用范围具有局限性；活度系数法虽然计算简单，但需要大量的实验数据，对于计算新型制冷剂时还有困难；传统意义上可以通过实验手段获得气液相平衡数据，但实验结构设计复杂、费用大，对于易燃易爆、带有毒性的制冷剂还具有一定的危险性[5]。

随着计算化学理论和计算机技术的发展，模拟仿真逐渐变成计算气液相平衡的主要工具之一[6]。赵胜喜等[7]利用吉布斯蒙特卡罗法模拟R410A的气液相平衡并得到临界状态点。陈秀萍等[8]对比了分子动力学、吉布斯系综蒙特卡罗和真实溶剂似导体屏蔽模型3种方法的热物性模拟结果，前两种计算方法由于目前分子间相互作用力理论不够完善，缺少专用于制冷剂的力场，势能函数的精度不够高，例如，力场中的势能参数具有局限性，不能描述所有物质，且大部分力场不能很好的处理分子间的静电作用，因此还存在一定误差。真实溶剂似导体屏蔽模型(COSMO-RS)[9]通过物质的分子结构信息来计算物质的气液相平衡，避开了势能函数精度的影响，只需要通过调节分子的尺寸因子。该方法允许快速并自洽的处理溶液中的分子，且在量子化学水平上最大程度的近似溶剂的特点：通过经典的介质理论描述溶剂与溶质的静电相互作用。陈秀萍等[10-11]采用COSMO-RS模拟了R290/R227ea和R290/R1234ze的气液相平衡数据，误差≤4%。Bai Zhenmin等[12]利用真实溶剂似导体屏蔽模型模拟了甲醛与水的气液相平衡，并与实验值对比，具有很好的一致性。但对于COSMO-RS在计算众多种类单工质制冷剂的气液相平衡时准确度是否会出现变化缺乏研究。因此本文针对无机物、碳氢化合物和氢氟烃3种不同化学类型的单工质制冷剂进行气液相平衡计算，并对其精度进行研究。

1 COSMO-RS理论

1.1 COSMO-RS理论

COSMO-RS是一种连续介质溶剂化模式，模型中将连续介质的介电常数设为无穷大(理想导体)，这样将屏蔽电荷限制在界面上，从而使分子和溶剂间没有电场，导体内也没有电荷[13-14]。COSMO-RS只需要物质的结构信息就可以通过对分子进行量子化学计算来预测多元体系的相平衡及其他热物性，是目前量子化学和工程热力学之间最好的连接手段。作为一种描述流体和热力学性质的方法，由于不需要实验数据，COSMO-RS发展迅速。

COSMO-RS建立在分子间片段对相互作用的概念上，即在COSMO-RS模型中将分子分解成面积大小相等的片段，分子间相互作用的概念建立在表面片段相互作用的物理观点上。用相互接触的片段对的净屏蔽电荷密度σ和σ′来计量两片段在真实体系和理想导体中的能量差别Emisfit，如式(1)所示。

(1)

式中：aeff为有效接触表面积， nm2；α′为能量因子，可由静电理论计算。若研究体系中还存在强极性物质，还需考虑氢键的相互作用EHB，如式(2)所示。

(2)

A=min(0,σdon+σhb)

(3)

B=max(0,σacc-σhb)

(4)

式中：σdon=min(σ,σ′)，σacc=max(σ,σ′)；σhb为氢键阈值；chb为强度系数。σhb、chb必须与实验值吻合。

式(2)、式(3)化简后主要有两种可能性：一是当两个相接触的表面屏蔽电荷中负极部分的电荷密度σ<-σhb；二是正极部分的电荷密度σ′>σhb，氢键为零。此时，正电荷是接受体，负电荷是供体。氢键正比于剩余部分电荷(σdon+σhb)(σacc-σhb)。

除了考虑Emisfit和Ehb外，还需要考虑分子片段间的范德华作用力Evdw，如式(5)所示。

(5)

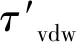
分子片段间相互作用的总能量可由式(6)得到：

E(σ,σ′)=Emisfit+EHB+Evdw

(6)

1.2 σ-profile

分子表面的屏蔽电荷密度σ是采用COSMO-RS理论最重要的数据。每个片段的表面屏蔽电荷密度能用一个合适的平均值表示，能满足相互配对。可以采用量子化学方法得到这些片段的表面电荷密度，并经过一个基于式(7)在半径为rav的面积上的平均。

(7)

式中：dij为片段i和片段j之间的距离，nm；ri为根据片段面积计算的片段i的平均半径，nm；rav为可调参数。

由分子表面所有片段的表面屏蔽电荷密度构成的整个分子的表面屏蔽电荷密度分布直方图，称为分子的表面屏蔽电荷密度分布函数P(σ)，亦称为分子的“σ-profile”，它表示在分子表面上找到具有平均屏蔽电荷密度为σ的面积的数量。

对于混合物S系综的表面屏蔽电荷密度分布函数Ps(σ)，是体系中各种组分Xi的PXi(σ)按其摩尔分数xi的加权平均，如式(8)所示。

PS(σ)=∑i∈SxiPXi(σ)

(8)

为方便进行统计热力学计算，对Ps(σ)进行归一化处理。由于每个分子的总表面积可以利用该分子的PXi(σ)在整个σ变化区间上积分求得，因而系综的标准屏蔽电荷密度分布函数可定义为：

(9)

式中：AXi为组分Xi的分子的总表面积，nm2，AS为系综S的分子的平均总表面积，nm2。

1.3 单工质饱和蒸气压计算

假定一个没有自由表面的大量液体系统，即分子的表面片段之间接触，该假设仅适用于远离临界状态的液体。在该假设条件下，系综的统计热力学可以按照式(10)计算:

(10)

(11)

式中：μS(σ)为系综S在温度T下，接触面积为aeff的片段化学势，kJ。由于μS(σ)存在于方程的两边，因此该方程采用迭代求解，μS(σ)初始值为零。

该片段的活度系数可由式(12)获得：

(12)

由式(10)和式(12)直接定义溶质X在系综S中的化学势：

(13)

(14)

(15)

式中：AS为溶质X分子的平均表面积，nm2；λ为调节参数。

在COSMO-RS理论中，除了预测液相工质的热力学性质，COSMO-RS理论还提出了一个方法，用于预测纯组分气相化学势。

(16)

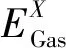
根据热力学理论，单一组分的饱和蒸气压可根据式(17)计算：

(17)

在COSMO-RS中，尺寸因子s是可调的，其缺省值为1.0，实际可根据实验值拟合。本文以气液相平衡数据为目标值，对各类制冷剂工质的尺寸因子进行拟合，获得了准确的气液相平衡数据。调节s将对溶质的液相化学势产生影响，从而影响式(17)，其中的理论依据还有待进一步探讨。

2 基于COSMO-RS的单工质的气液相平衡模拟

制冷剂按化学组成分类，主要有无机物、碳氢化合物(HCs)和卤化物(氟利昂)3类。由于具有相似化学组成的化合物在COSMO中生成屏蔽电荷的分布具有相似性，对尺寸因子s的规律寻找也具有一定的指引。基于臭氧层的保护，氟利昂制冷剂中CFCs已被淘汰使用，HCFCs也已被限定使用期限。氢氟烃类简称HFCs，臭氧层的破坏系数为0，但气候变暖潜能值(GWP)很高，被视为CFCs和HCFCs类物质的重要过渡性替代物质。目前HFCs的大气浓度较低，对于气候变化的作用很小[15]。制冷系统的工作温度范围(蒸发温度～冷凝温度)通常为-20～60 ℃，因此本文模拟的温度范围为250～330 K，部分工质的模拟温度根据其临界点做出调整。外延到其他温区范围时，根据外延温区范围的增大，误差变大，约为±10%，可以通过调节s值来减小该误差。模拟给定的迭代起点温度大部分设定为273.15 K，部分迭代起点温度为模拟温度上限和下限的中间值。在计算中，s以与制冷剂特性查询软件NIST的最大误差最小来调解。

s与分子化学组成和工作温度范围密切相关。由于制冷剂的工作环境有一定的限制，因此将工作温度限制在一定温度范围内(250～330 K)。限制了温度对s的影响。同时对于制冷剂化学组成的分类也降低了s变化规律的不确定性。

2.1 无机物制冷剂的气液相平衡模拟

图1 无机物制冷剂的气液相平衡曲线模拟值与NIST值对比Fig.1 The comparison curve of inorganic refrigerant between simulated value and NIST value of gas-liquid equilibrium

无机物是制冷剂发展的第一个阶段[16]，无机物制冷剂不破坏臭氧层，产生温室效应极小，且获取容易、价格低廉。其中CO2和NH3是最常见的两种无机物制冷剂。利用COSMO-RS理论对这两种无机物制冷剂进行气液相平衡数据的模拟，模拟结果如图1所示。图1中，左上角曲线图为气液相平衡压力模拟值与NIST值的相对误差，右上角为该分子的表面电荷密度图。模拟中发现，当s=1.0时，计算值误差较大。因此，逐渐改变s，发现通过调节分子的s，可使模拟的气液相平衡曲线逐渐接近NIST的实验值。图1(a)中左上角的图显示了s对相对误差的影响。图中模拟结果与NIST值之间的相对误差通过式(18)计算：

(18)

式中：pS为模拟压力，MPa；pN为对应温度和压力下NIST中的压力， MPa。

由图1(a)可知，模拟的气液相平衡曲线与NIST提供的气液相平衡曲线趋势完全一致。当CO2的s=4.4时，在低温区和高温区相对误差较大，但仍在±2.5%以内。图1(b)中当NH3的s=0.37时，最大相对误差δmax在±1.0%以内。

2.2 碳氢化合物制冷剂的气液相平衡模拟

碳氢化合物的制冷剂包括烷烃类和烯烃类，属于天然工质，因此对大气无污染、对臭氧层勿破坏和温室效应几乎为零。但碳氢化合物作为制冷剂时，可燃性、安全性需要特别注意。利用COSMO-RS理论对部分碳氢化合物进行气液相平衡模拟，烷类碳氢化合物的计算结果、模拟结果与NIST的相对误差如图2所示。

除了甲烷的模拟温度在130～190 K,其余3种烷类碳氢化合物的模拟温度范围均在250～330 K之间。CH4的s=1时，δmax在±2%以内；乙烷、丙烷和丁烷的s分别为0.004、0.002和0.0001时，乙烷和丙烷的δmax在±1%以内，丁烷的δmax在±3%以内，与NIST值均具有很好的一致性。图2(e)和图2(f)分别为乙烯和丙烯的气液相平衡曲线计算结果。由图2(e)可知，当乙烯的s=1.25时，δmax在±3%以内；由图2(f)可知，丙烯的s=4.1时，δmax在±1.5%以内。

2.3 氢氟烃类制冷剂的气液相平衡模拟

相对于碳氢化合物，氢氟烃类制冷剂的化学结构不对称。主要针对14种不同的氢氟烃类制冷剂进行气液相平衡的模拟。模拟结果及与NIST的相对误差如图3所示。

碳氢化合物中的氢原子被氟原子替代后，尺寸因子发生变化。选择合适的尺寸因子后，12种氢氟烷(HFCs)和2种氢氟烯(HFOs)类工质在模拟温度范围内，相平衡曲线模拟值与NIST值均具有很好的一致性，δ<±2%，仅C4F10的δ<±6%。

2.4 尺寸因子变化规律分析

表1所示为22种单工质的尺寸因子。

图4所示为烷烃化合物的s随碳原子的变化，s随着碳原子的增加而减小，纵坐标取对数坐标时，近似呈线性变化。

图5所示为全氟碳化合物(CnF2n+2)的s随碳原子的变化，s也随碳原子数的增加而减小，纵坐标取对数坐标时，呈较好的线性分布。

甲烷的氟化物(CHnF(4-n))、乙烷的氟化物(C2HnF(6-n))、丙烷的氟化物(C3HnF(8-n))的s随氟原子数的变化如图6所示。由图6可知，s随氟原子数的增大而增大，但全氟替代物CF4、C2F6、C3F8的s突然大幅减小，甚至小于对应的烷类。这是由于氟原子间的相互吸引力较大所致。图6中的变化趋势完全一致，即先缓慢增大，最后突然增大，又急剧减小。

甲烷、乙烷和丙烷的氟化物都可以根据图表中的规律选取相应的s范围。对于烷类化合物及烷类氟化物，在模拟温度范围内可以预测出s的数值范围，在数值范围内，预测出的模拟数据对实验具有一定的指导作用。因此，可以根据s的变化规律，在已知化合物分子结构的情况下，根据一个相平衡点和s，对没有实验数据的未知化合物的气液相平衡数据进行预测，其准确度约为±2%。

2.5 饱和蒸气压方程拟合

饱和蒸气压的计算在工程中非常重要，可以由状态方程导出，但较为复杂，故工程上通常采用直接回归的饱和蒸气压方程。饱和蒸气压的形式很多，常用的有Antoine方程和Wagner方程。三参数的Antoine方程是工程上最常用的饱和蒸气压方程，特点是简单、系数少、较为精确[17]。其形式为：

(19)

图2 碳氢化合物制冷剂的气液相平衡曲线模拟值与NIST值对比Fig.2 The comparison curve of HCs refrigerant between simulated value and NIST value of gas-liquid equilibrium

分类工质尺寸因子s工质尺寸因子s无机物CO2(R744)4.4NH3(R717)0.37烷烃CH4(R50)1C2H6(R170)0.02C3H8(R290)0.002C4H10(R600)0.000 1烯烃C2H4(R1150)1.25C3H6(R1270)4.1HFCsCH2F2(R32)1.8CHF3 (R23)4.9CF4 (R14)0.001 2C2H4F2 (R152a)1.5C2H3F3 (R143a)2.5C2H2F4 (R134a)3.2C2HF5 (R125)8.5C2F6 (R116)0.000 3C3H3F5 (R245fa)2.7C3HF7 (R227ea)15C3F8 (R218)0.000 06C4F100.000 02HFOsC3H2F4(R1234ze)3.7C3H2F4(R1234yf)6.1

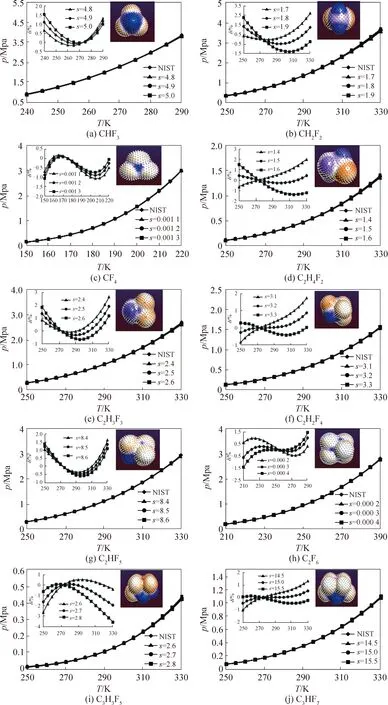
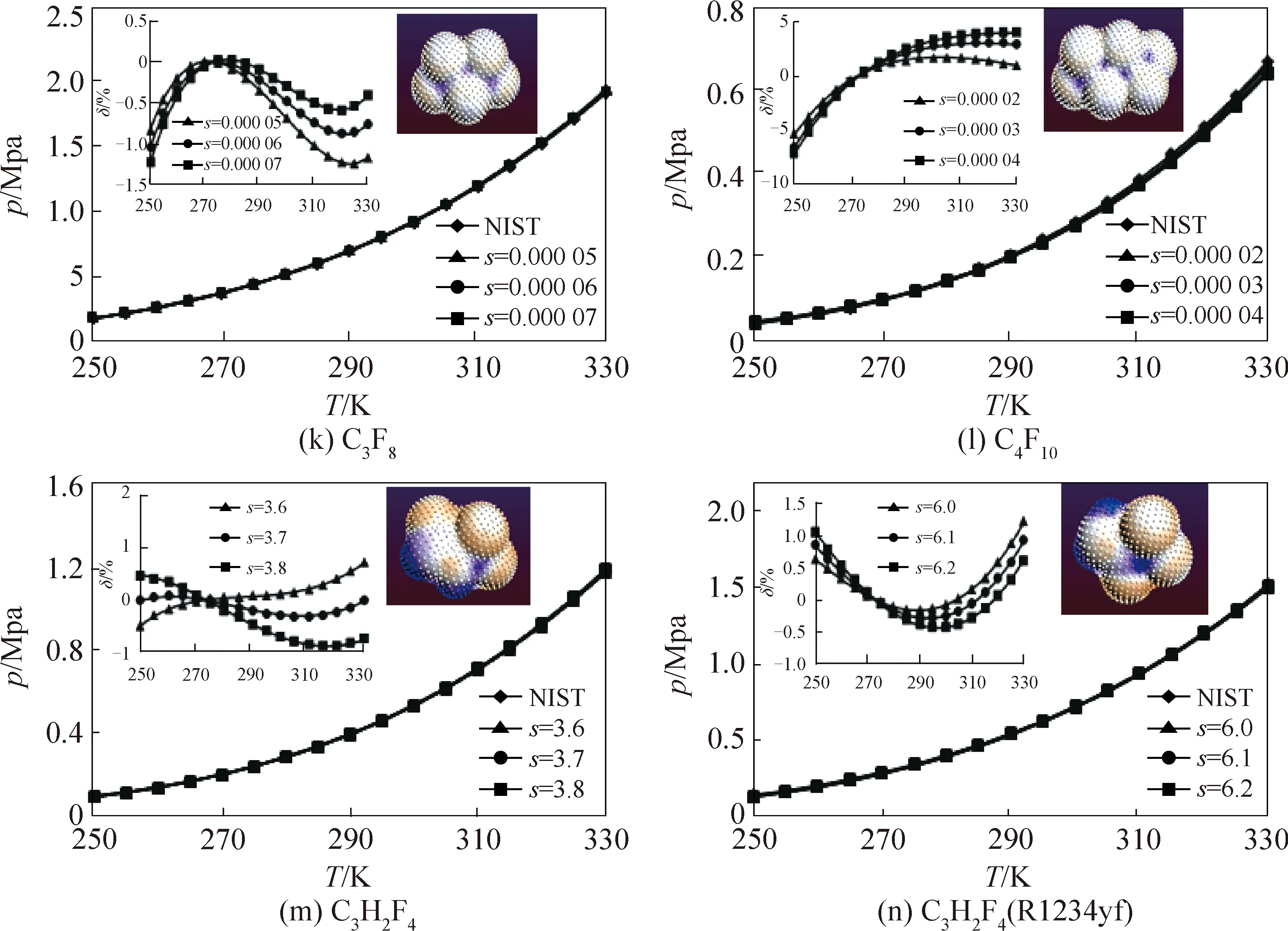
图3 氢氟烃类制冷剂的气液相平衡曲线模拟值与NIST值对比Fig.3 The comparison curve of HFCs refrigerant between simulated value and NIST value of gas-liquid equilibrium

图4 烷烃类(CnH(2n+2))工质s值碳原子数的变化Fig.4 The variation trend of scale factor of CnH(2n+2)with the number of carbon atoms

图5 全氟化烷类(CnF(2n+2))工质s随碳原子数的变化Fig.5 The variation trend of scale factor of CnF(2n+2) with the number of carbon atoms

图6 甲烷氟化物、乙烷氟化物、丙烷氟化物工质s随氟原子数的变化Fig.6 The variation trend of scale factor of CHnF(4-n)，C2HnF(6-n) and C3HnF(8-n) with the number of carbon atoms

式中：p为压力，MPa；T为温度，℃，a1、a2、a3均为常数由模拟数据拟合得出。表2所示为Antoine方程中各工质的三参数及拟合出的Antoine方程中饱和压力与模拟出的饱和压力之间的平均误差，平均偏差定义为：

(20)

式中：pA为Antoine状态方程计算的压力值，MPa；pS为模拟出的饱和压力，MPa。

由表2可知，拟合曲线与模拟数据之间的平均偏差很小，拟合出的Antoine方程在模拟的温度范围内与模拟数据具有较高的一致性。

表2 Antoine方程中各工质的参数拟合及拟合方程与模拟值偏差Tab.2 The parameters in Antoine equation and the deviation between the value of fitting equation and simulated value

3 结论

本文采用COSMO-RS模型研究了纯制冷剂工质的气液相平衡的热物性,总结了不同种类单工质尺寸因子的变化规律。对比模拟结果与NIST提供的数据，无机物CO2和NH3的相对误差分别在±3%和±1%以内；烷类和烯类(HCs)的相对误差均在±3%以内；氢氟烃类(HFCs)的相对误差均在±2%以内，除了C4F10的相对误差在±6%以内。因此，COSMO-RS气液相平衡模拟结果与NIST提供的数据具有很好的一致性。得到尺寸因子的变化规律如下：

1)烷烃类工质CnH2n+2的尺寸因子随碳原子数的增加而减小。

2)全氟化烷类工质CnF2n+2的尺寸因子随碳原子数的增加而减小。

3)氢氟烷类工质CnHF2n+1(HFCs)的尺寸因子随氟原子数的增加而增大；但当氢原子全部被氟原子替代后，尺寸因子又大幅减小，甚至小于相对应的烷烃类。

4)氢氟烯类工质CnHF2n-1(HFOs)的尺寸因子随氟原子数的增加而增大。

5)根据模拟数据拟合出Antoine方程的系数。

根据以上尺寸因子的变化规律，结合分子结构，以及至少一点的气液相平衡数据，可以预测新型单工质制冷剂的气液相平衡曲线。