化学元素对热轧带肋钢筋性能的影响

高 源 ，颜靖柯 ，冯 意

（1.四川工商学院计算机学院，四川 成都 611745 2.四川工商学院云计算与智能信息处理重点实验室，四川 成都 611745）

1 引言

热轧带肋钢筋的俗称是螺纹钢，也叫“变形钢筋”[1]，广泛用于房屋、桥梁、道路等土建工程建设上。热轧带肋钢筋大多在钢中添加昂贵的微量元素调整成分比例，改善结构性能。一个好的组合设计可以保证性能，同时有效地控制生产成本。张雪亚等通过相关性分析得出了影响螺纹钢力学性能的主要因素，并以此结果建立优化模型，最终得出当Cr含量的增加量不超过 0.0720，C，Mn，Si，Ce，V，Cu 含量的减少量分别不超过某一数值时，可以最大限度的提高螺纹钢的力学性能[2]；黄超团队利用主成分分析法和多元线性回归得出化学元素与三大评估指标的关系，但未考虑到此类问题是一个复杂的多元耦合系统[3]；吕静毅等也通过多元逐步回归分析了影响螺纹钢抗拉强度、屈服强度、断后伸长率的主要元素，但化学元素在不断加入过程中，会对已加入的元素造成影响，可能得不出正确的影响权重，有待改进[4]。在本文中，先通过多元逐步回归筛选出对三大评估指标有较大的影响的元素。考虑到在多元耦合系统中，为找出确实可靠的主要影响因素。所以用灰色关联分析从非线性的角度得出不同化学元素对钢筋性能影响的主、次之别。现有某企业两种热轧带肋钢筋产品近两年的生产数据，利用这些数据分析影响变形钢筋性能的主要因素，如屈服强度，抗拉强度和断后伸长率等，并分析这些因素之间的相关性。

2 总体思路分析

据分析，将附件分为group1和group2两组数据后，对比分析两组数据中化学元素对钢筋性能的影响。钢筋性能的评估指标有抗拉强度、屈服强度和断后伸长率，通过分析化学元素分别对三大评估指标的影响，体现出化学元素影响到了钢筋性能，如图1。

2.1 数据清洗

据统计，初步推断钢的化学成分与低合金高强钢的性能一般呈线性相关。根据产品的规格将附件1的数据分成两个图表。根据材料力学定理，屈服强度的值小于抗拉强度的值，由其定义决定。使用抗拉强度和屈服强度之间的差异来衡量数据是否有效。输入数据并绘制散点图：

由于图中的异常点与平均值的差异较大，所含数据不符合本课题的计算要求，会对计算造成干扰。丢弃异常点，如图2和图3所示。

图2 产品1抗拉、屈服强度之差与序列点的散点图

图3 产品2抗拉、屈服强度之差与序列点的散点图

2.2 多元逐步回归分析

热轧带肋钢筋强度的变化受多种元素含量的影响。在供选择的n个自变量中，依各自变量对因变量作用的大小，即偏回归平方和的大小，由大到小把自变量依次逐个引入。每引入一个变量，就对它进行假设检验。当时，将该自变量引入回归方程。新变量引入回归方程后，对方程中原有的自变量也要进行假设检验，并把贡献最小且退化为不显著的自变量逐个剔除方程。最后所得方程即为所取得的“最优”回归方程。

多元逐步回归方程[5]和多元线性回归方程的表达式相同：

表示因变量，表示自变量，表示要估计的参数，表示随机干扰项。随机误差项具有零均值，协方差和序列非相关性。下一步，在验证和分类图上启动多元逐步回归分析过程，并借助SPSS建立回归方程。

3 多元逐步回归下的变量相关性分析

3.1 组1（产品1）

3.1.1 抗拉强度与元素的关系

首先以抗拉强度为因变量，根据参考文献[5]以及实际附件数据可知，除了Mo之外，其它元素如C，Mn，S，P，Si，Cr，Cu，Ni，Alt，V 等与抗拉强度都有线性关系可作为决定变量输入spss中进行回归计算。查阅资料可知，化学元素对钢筋性能的影响是一个复杂的多元耦合系统，每次新加入一个元素进去会对已经加入的元素效果造成影响。最终通过spss自动分析，模拟依次加入元素的过程，综合分析其中的关系，排除对抗拉强度影响甚微的元素。排除过程见表1：

通过上表的第七次排除过程，可以得出对抗拉强度效果影响甚微的元素为 P、Ceq、Ni、Alt，所以排除这四个元素。因为是复杂的多元耦合系统，在依次不断加入元素的过程中，对抗拉强度有影响元素的相关系数也是随着该过程不断变化的。下表2就是相关元素系数随着加入过程不断变化的流程。

在逐步回归方程中，水平上，因变量与各自自变量之间存在相关关系，具有显著性。线性方程如下。

Yts1是指产品1的抗拉强度

由于线性方程中随机因素的影响，对常数ε进行残差分析很重要[6][7]。计算公式如下所示。

ei是指残差；yi是指观察值；是指预测值。如果残差分析的结果遵循正态分布，则回归分析生成的线性方程符合要求。残差分析的结果如图4所示。

从图中可以看出，的残差分析遵循正态分布，所以线性方程是正确的。

3.1.2 屈服强度与元素的关系

屈服强度与元素的关系和上面抗拉强度的分析方法一样，排除过程如下表3：

通过上表的第七次排除过程，我们可以得出对屈服强度效果影响甚微的元素为 S、P、Ceq、Ni，所以排除这四个元素。

表1 排除变量的过程

图4 抗拉强度线性方程的残差分析

表3 屈服强度有关元素一到七次变量排除过程

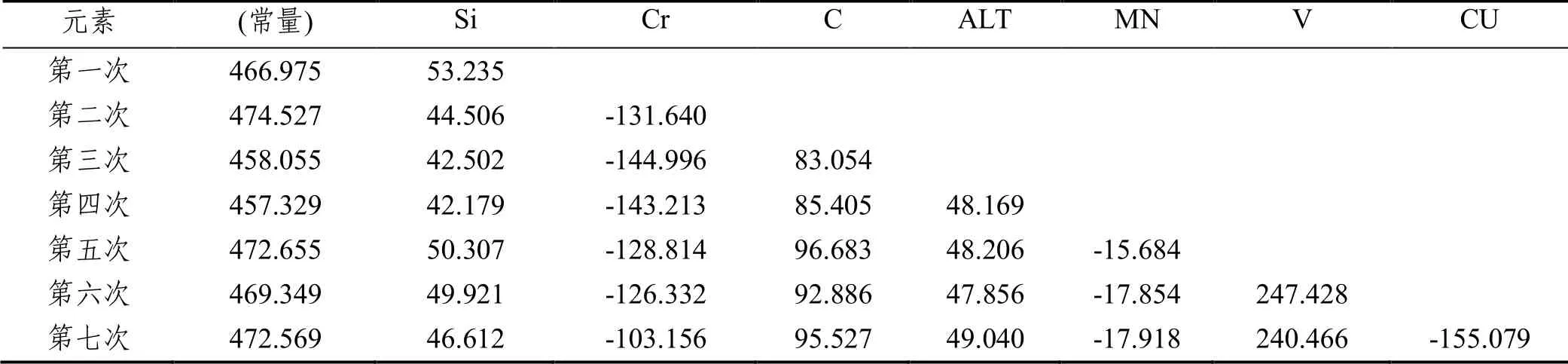
表4 基于多元逐步回归的相关元素对屈服强度回归方程系数的变化过程

由表4第七次所得系数可知，线性方程如下：

Yys1指产品1的屈服强度。

残差分析的结果如图5所示。从图中可以看出，ε的残差分析遵循正态分布，所以线性方程是正确的。

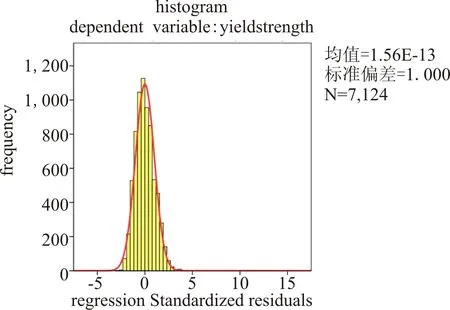
图5 屈服强度线性方程的残差分析

3.1.3 断后伸长率与元素的关系

断后伸长率与元素的关系和前面方法同理，排除过程如下表5：

表5 断后伸长率有关元素一到七次变量排除过程

表6 基于多元逐步回归的相关元素对断后伸长率回归方程系数的变化过程

由表6第九次所得系数可知，线性方程如下：

Ypef1是指产品1断裂后的伸长率，残差分析的结果如图6所示。从图中可以看出，ε的残差分析遵循正态分布。所以线性方程是正确的。

图6 断后伸长率线性方程的残差分析

3.2 第2组（产品2）

3.2.1 抗拉强度与元素的关系

产品2抗拉强度与元素的关系分析同上。排除过程如下表7：

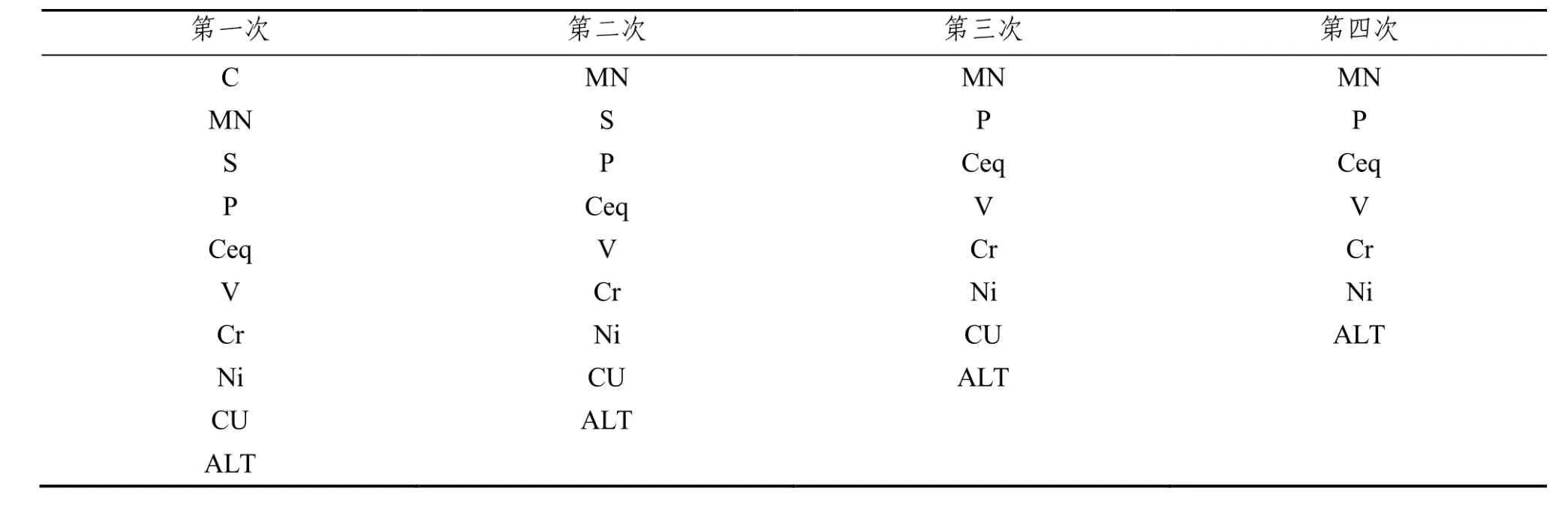
表7 抗拉强度有关元素一到四次变量排除过程

通过上表的第4次排除过程，我们可以得出对屈服强度效果影响甚微的元素为 Mn、P、Ceq、V、Cr、Ni、Alt，所以排除这 7 个元素。

表8 基于多元逐步回归的相关元素对抗拉强度回归方程系数的变化过程

由表8第四次所得系数可知，线性方程如下： Yts2是指产品2的抗拉强度，残差分析的结果如图7所示。

图7 抗拉强度线性方程的残差分析

从图中可以看出，ε的残差分析遵循正态分布，所以线性方程是正确的。

产品2屈服强度与元素的关系分析同上。排除过程如下表9：

3.2.2 屈服强度与元素的关系

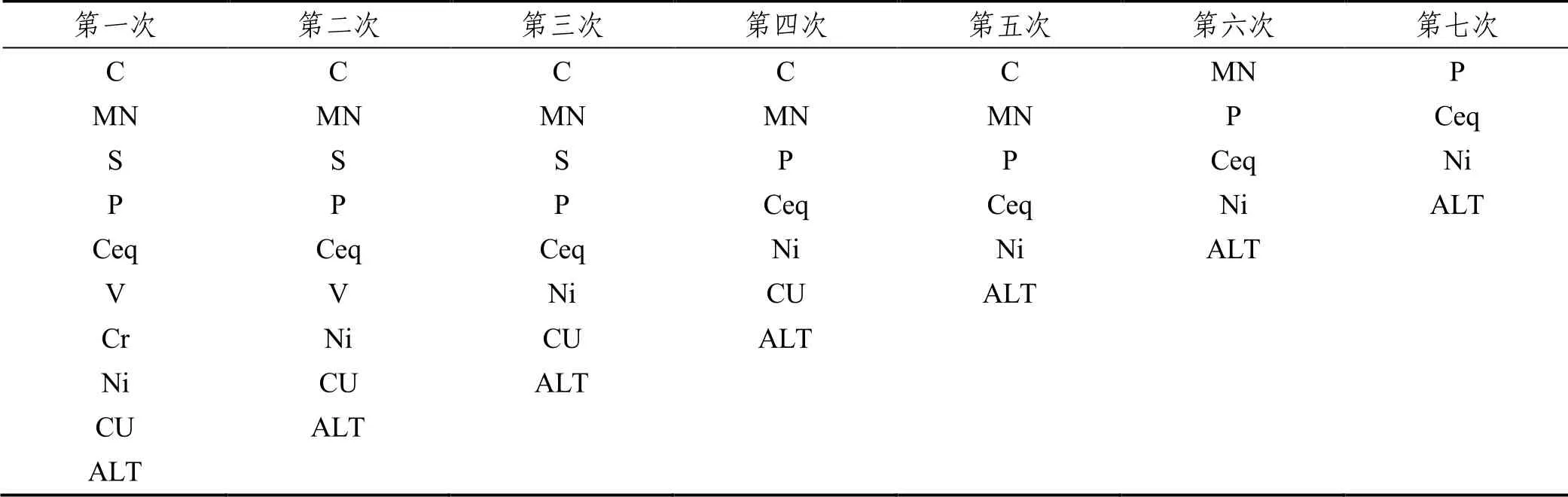
表9 屈服强度有关元素一到七次变量排除过程

通过上表的第7次排除过程，我们可以得出对屈服强度效果影响甚微的元素为 P、Ceq、Ni、Alt，所以排除这4个元素。

表10 基于多元逐步回归的相关元素对屈服强度回归方程系数的变化过程

从上表10第七次系数可得线性方程：

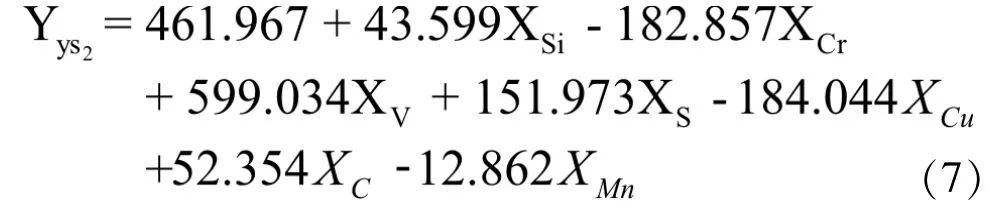
Yys2是指产品2的屈服强度。

残差分析的结果如上图8所示。

从图中可以看出，ε的残差分析遵循正态分布，所以线性方程是正确的。

图8 屈服强度线性方程的残差分析

3.2.3 断后伸长率与元素的关系

产品2断后伸长率与元素的关系分析同上。排除过程如下表11：

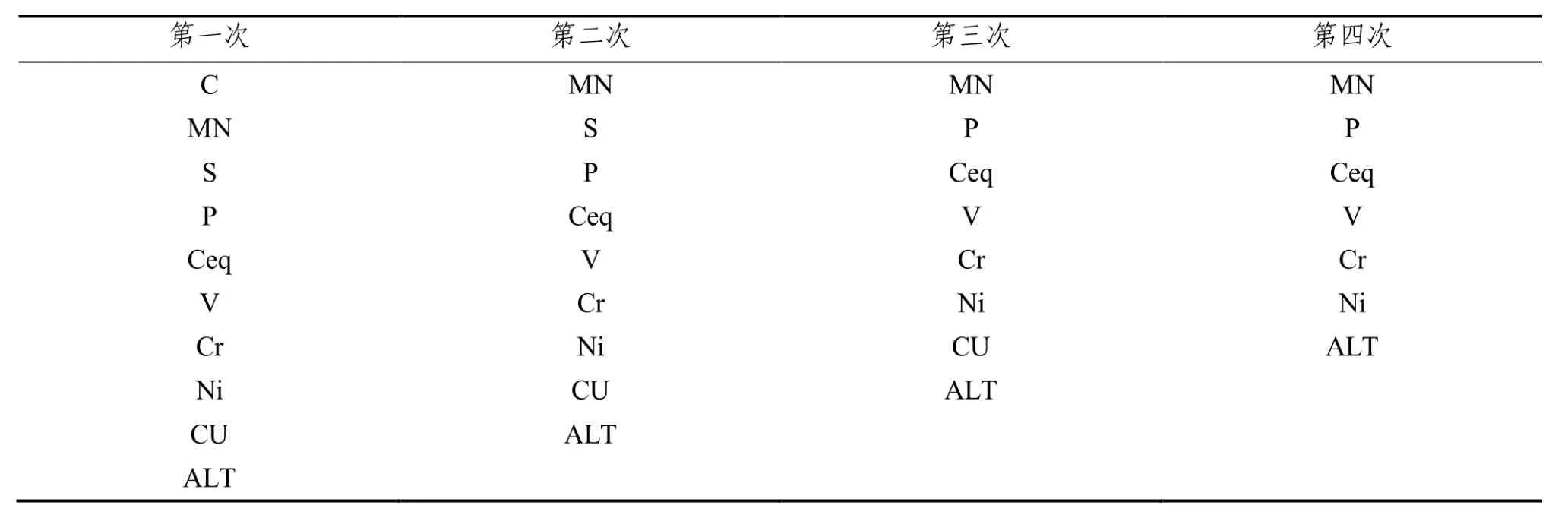
表11 断后伸长率有关元素一到四次变量排除过程

通过上表11的第4次排除过程，我们可以得出对断后伸长率效果影响甚微的元素为Mn、P、Ceq、V、Cr、Ni、Alt，所以排除这 7 个元素。

表12 基于多元逐步回归的相关元素对断后伸长率回归方程系数的变化过程

从上表12第四次系数获得的线性方程：

Ypef2是指产品2断裂后的伸长率。残留分析结果如上图9所示。

从图中可以看出，ε的残差分析遵循正态分布。所以线性方程是正确的。

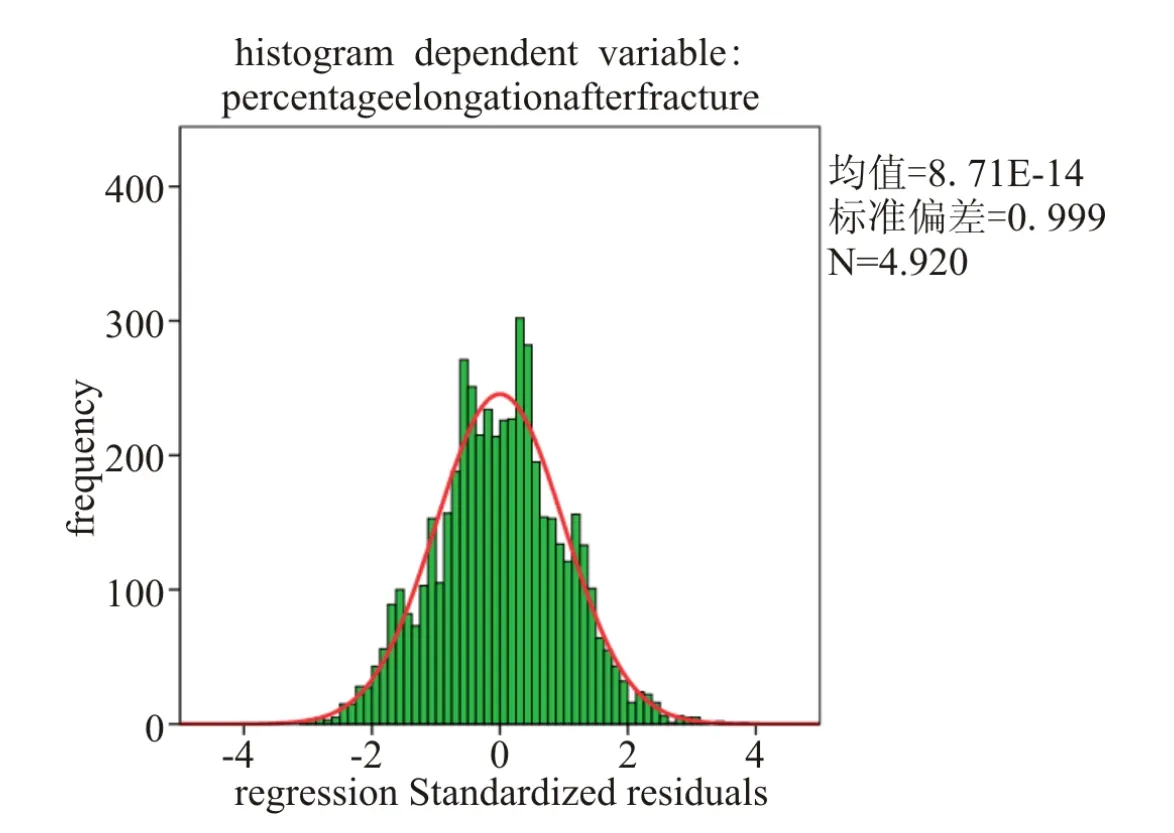
图9 断后伸长率线性方程的残差分析

3.3 数据分析结论

通过逐步回归和残差分析的方法，对数据表中各成分与抗拉强度，屈服强度，断后伸长率的关系进行逐步回归分析。

根据1号钢和2号钢中各种元素的含量以及参数估计值，综合化学元素对两种产品的影响，得出如表13的结果：

表13 影响钢筋性能的主要元素

以上结果反映了哪些元素对钢筋性能的三方面因素体现有明显的影响。但是逐步多元回归分析因在不断加入新元素时对已加入的元素有所影响，则在确定主要和次要变量时存在困难。灰色关联分析擅长处理分析出主要因素和次要因素，所以接下来进一步使用灰色关联分析确定影响钢筋性能的最主要因素。

4 基于灰色关联分析确定影响钢筋性能的主要因素

4.1 问题分析

根据背景资料显示，不同百分比下的不同元素对钢的性能有不同的影响。但影响钢铁业绩的主要因素到底是哪些元素，内部的具体影响是不确定的。 因此，化学元素对变形钢筋性能影响的系统是一个灰色系统。我们可以使用灰色关联分析方法[8][9]找到比较序列（12个元素）和参考序列（3个性质）的相关矩阵。然后根据比较结果确定主要因素和次要因素，分析相关程度。

另一方面，主要因素和次要因素可能影响钢材的相同性能，因此它们之间是否存在相关关系也是不确定的。我们也认为主要因素与次要因素之间的相关性是一个灰色系统。 采用灰色关联分析的方法主要因素与次要因素的相关矩阵，然后求解并找出它们之间是否存在相关关系。

4.2 灰色关联分析的方法和原理

根据灰色系统理论[10]，将钢筋的1，2规格作为灰色系统，对系统中各种化学元素与钢筋性能的相关度进行了模拟。根据相关程度的大小来分析，确定哪些化学元素的含量是影响钢筋性能的主要因素。以下是灰色关联分析的具体步骤：

(1)确认比较对象和参考序列。 C，Mn，S，P，Si，Cr，Mo，Cu，Ni，Alt，V 等化学元素及 Ceq 含量为 12个评价对象这也意味着参考序列是：

比较顺序是：

灰色相关系数计算如下：

ξi(k)是相关系数[11]，ρє[0,1]是区分系数

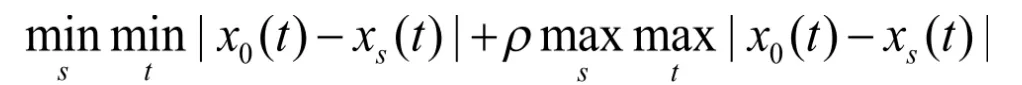
是最小的差异和两级之间的最大差异。

(2)计算灰色关联度，公式为：

(3)评估和分析。对于多于一个的参考序列，并且比较的因子是多于一个的情况。我们应该使用上行分析。换句话说，对于每个参考序列，有12个比较序列和12个相关度。根据矩阵中的元素进行模拟后，找出相关矩阵R是大还是小。我们可以分析和确定哪些因素起主要作用，哪些因素起到次要作用。主要影响因素也被称为主导因素。

4.3 灰色关联度计算

(1)标准化原始数据[12]。由于P，S会使钢材产生冷热脆性，则P、S元素的比例可能会更低。公式：

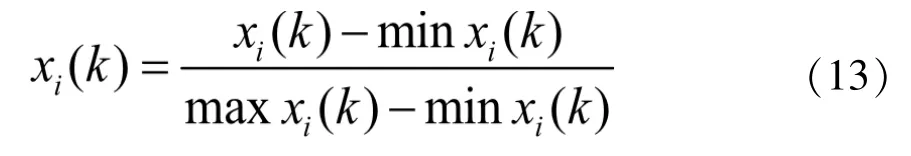
在一定范围内， 随着 C，Mn，Si，V，Cr，Ni，Cu，M0，Alt等百分含量的增加，钢的性能更好，有利于钢筋性能的影响。用原始数据标准化公式：

(2)找出参考序列和比较之间的差异，并用公式进行模拟：

(3)模拟相关系数和相关程度，找出相关矩阵R。分析确定影响变形钢筋性能的主要因素和次要因素。

(4)利用灰色关联分析方法找出主要与次要因素的相关矩阵，然后分析它们之间的相关关系，ρ=0.5。

表14列出了12个子因素与3个母因素之间的相关矩阵评估指标、参考指标。

规定相关度大于0.995的化学元素是主要因素[13]。据表14所示的相关矩阵，四个因素（Ceq，C，V，Mn）大于0.995。其中Ceq将各种合金元素转化为热轧带肋钢中的碳含量，它不是一种化学元素。是为了便于表达这些材料的强度性能和焊接性能，而且Ceq本身就是描述钢筋性能的一个表现，所以将Ceq 删除。其它化学元素按 C，V，Mn，Si，P，S，Cu，Ni，Cr，Alt，Mo等级排列，C，V，Mn 大于 0.995，断裂伸长的相关程度也在前三位。所以我们认为C，V，Mn是影响钢筋性能的主要因素，其他因素是次要因素。

表14 各因素之间的相关关系

4.4 主要因素与次要因素的相关程度分析

根据上诉，用同样的方法分析主要因素与次要因素的相关性。3个元素C，V，Mn是主要因素，其余8个元素是次要因素。找到相关矩阵，判断其相关性。相关矩阵见下表15：

我们规定相关度大于0.90的元素意味着次要元素与主要元素有关。因此表15相关矩阵中的Al，Mo，Ni，Cu四种次要元素和主要元素有很大关系。从背景资料可以看出，Al可以作为脱氧剂，与V，Mn起同样的作用。

表15 主要与次要因素的相关程度结果

5 结论

本课题采用了更适合分析钢筋性能这类复杂多元耦合系统的方法，即多元逐步回归分析。利用相关化学元素的值分别对产品1和产品2的抗拉强度、屈服强度、断后伸长率做相关性分析。综合产品1和产品2的结果，得出与抗拉强度有影响的元素有 Mn、C、V、S、Si、CU、Cr；与屈服强度有影响的元素有 Si、Cr、C、ALT、Mn、V、CU、S；与断后伸长率有影响的元素有 V、ALT、Ni、S、P、Cr、C、Ceq、Si、Cu。但这还不足以反映出哪些元素与抗拉强度、屈服强度、断后伸长率关系最紧密，即主要因素。通过灰色关联度计算得出C，V，Mn是影响钢筋性能的主要因素，Al与主要元素有较大的相关性，已知Mo，Ni，Cu可在一定范围内提高钢的强度和韧性，再结合表15的相关程度数值，进一步验证了结果的准确性。