再生骨料透水混凝土性能的统计规律分析

陈守开，陈家林，符永淇文，张政男，蒋海峰

（1．华北水利水电大学 水利学院，河南郑州450045；2．河南省水环境模拟与治理重点实验室，河南 郑州450045；3．河南省水环境治理与生态修复院士工作站，河南郑州450002；4．水资源高效利用与保障工程河南省协同创新中心，河南郑州450045）

近年来，建筑垃圾的年产量逐步增加，现已成为污染环境的重要因素。据统计，我国建筑垃圾产生量以每年10%～20%的速率增长，预计2020年将突破30亿t［1］。 再生骨料透水混凝土（Recycled Aggregate Permeable Concrete，RAPC）是将建筑垃圾经过一系列处理后与水、水泥按一定的比例制备而成，具有透水、透气且质量轻的特点，其作为绿色生态型混凝土，不仅能有效缓解城市热岛效应和减轻城市排水系统压力［2］，提升城市生态系统功能和减少城市洪涝灾害的发生［3-4］，而且能够促进废弃混凝土的资源化利用［5-6］，减少建筑垃圾带来的环境污染问题。

Khoshkenari等［7］研究了再生骨料混凝土抗压强度与劈拉强度之间的关系，通过建立回归线性模型确定二者的关联性；Rizvi等［8］通过RAPC性能试验，认为抗压强度与透水系数之间存在负相关关系；袁汉卿等［9］在不同再生骨料取代率的条件下，分析了RAPC抗压强度与透水系数的变化趋势并确定二者之间的相关性；薛如政等［10］、张浩博等［11］、陈守开等［12-13］也得出了类似结果。此外，Sun等［14］构建了支持向量机模型、Shirgir等［15］构建了人工神经网络模型，通过相同输入因素预测透水混凝土的抗压强度与透水系数，预测精度较高，说明二者之间存在关联。由上述文献可知，RAPC各性能之间的确存在相关关系，但目前从统计学角度尚未有对其描述的报道。为此，笔者对RAPC性能试验数据进行统计分析，在一元正态分布的基础上，考虑RAPC各性能之间的联系，引入多维正态分布理论，提出由抗压强度、劈拉强度、孔隙率及透水系数构成的多维随机向量能够服从多维正态分布的假设，根据求得的协方差矩阵确定RAPC各性能之间的相关性，并基于χ2统计量的Q-Q图检验法进行正态性检验，为RAPC的研究与应用提供参考。

1 RAPC试验

1．1 RAPC原材料、配合比及制备工艺

RAPC试验用原材料包括：①拌和水用郑州市自来水；②水泥用河南丰博天瑞集团生产的天瑞牌P．O 42．5普通硅酸盐水泥；③再生骨料用强度等级为30 MPa的废弃混凝土路面经破碎、分级、清洗等工序获得粒径为10～20 mm的再生骨料，并依据规范测得其物理力学性能指标（表1）；④掺和料为粉煤灰、再生微粉及硅粉，采用等质量替代水泥的掺加方式，纤维为聚丙烯纤维、碳纤维，采用普通的掺加方式。

表1 再生骨料物理力学性能指标

本次试验以0．3水胶比，水泥、再生骨料、水（考虑附加水）用量分别为 327．59 kg／m3、1 474．14 kg／m3、98．28 kg／m3作为基准［4，6，12-13，16］。 掺合料和纤维的掺量见表2。

表2 掺和料与纤维掺量 %

试样制备工艺严格执行规范，将搅拌均匀的RAPC装模并在自然条件下养护24 h（保证试件成型），然后放入标准养护室养护28 d。

1．2 RAPC性能试验方法

（1）强度性能试验。RAPC强度性能包括抗压强度与劈拉强度，试验方法参照《普通混凝土力学性能试验方法标准》（GB／T 50081—2002），试件尺寸均为φ100 mm×200 mm的圆柱体，且均在WAW-1000型电液伺服万能试验机上完成，见图1。

图1 RAPC抗压强度与劈拉强度试验

（2）孔隙率与透水系数试验。RAPC孔隙率试验依据《再生骨料透水混凝土应用技术规程》（CJJ／T 253—2016）完成；透水系数试验基于达西定律的定水头法，采用自制的透水装置（图2）完成。

1．3 RAPC性能试验结果

本次通过试验共获得54组实测数据（表3）。RAPC抗压强度、劈拉强度、孔隙率及透水系数的实测范围分别为 2．86 ～ 10．60 MPa、0．95 ～ 2．28 MPa、14．34%～30．79% 及 2．36 ～ 4．68 mm／s，均满足规范要求。

图2 RAPC透水系数试验示意与装置

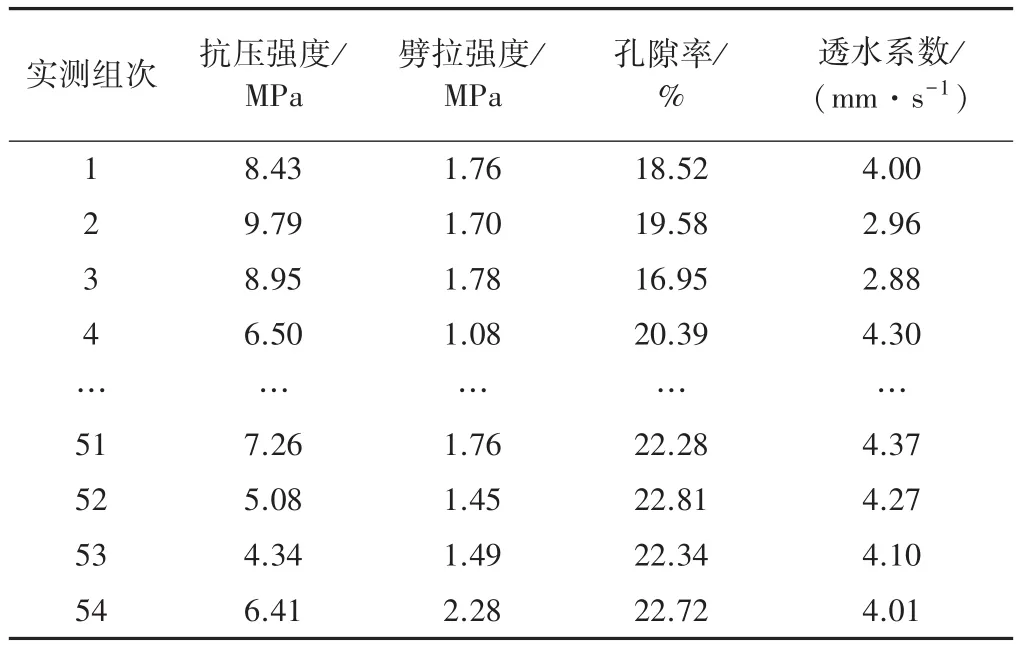
表3 RAPC各性能部分实测数据

2 正态分布统计及检验

2．1 正态分布统计

将RAPC抗压强度、劈拉强度、孔隙率及透水系数分别看作4个随机变量，根据上述实测数据，计算各随机变量的均值、标准差及方差等参数，均值分别为6．65 MPa、1．51 MPa、22．56%及 3．99 mm／s，标准差分别为1．74 MPa、0．29 MPa、3．72%及 0．50 mm／s，进而求得其方差分别为 3．02 MPa、0．08 MPa、13．84%及0．25 mm／s。

依据各随机变量均值、标准差、方差以及正态分布概率密度公式，求得各变量概率密度：

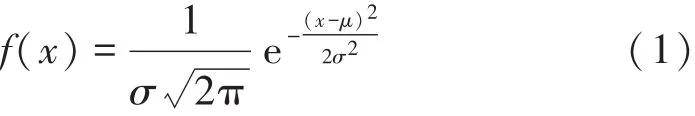
式中：f（x）为随机变量的概率密度；x为随机变量；μ为随机变量的均值；σ为随机变量的标准差；σ2为随机变量的方差。

依据式（1）求得的概率密度绘制RAPC各随机变量的频率分布曲线（图3）。

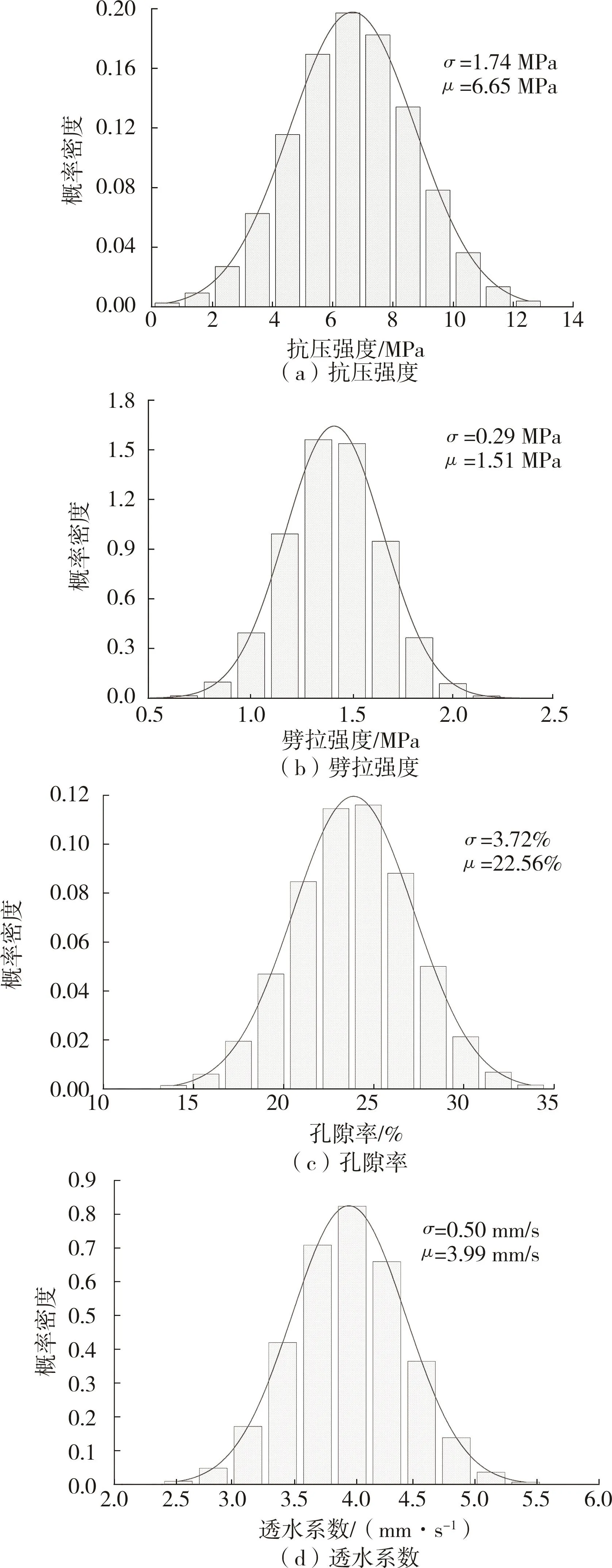
图3 RAPC各随机变量频率分布

2．2 正态性检验

采用K-S检验法在置信区间为95%的条件下，检验RAPC各性能的正态性，结果见表4。

表4 K-S检验结果

3 多维正态分布及参数确定

3．1 多维正态分布

现有的水泥基材料性能统计［17-18］，多数以单个性能作为随机变量进行分析，一般不考虑其性能之间存在的内在联系，缺乏真实性与完整性。已有研究表明，RAPC各性能之间存在必然且复杂的联系，且相关度较高［8-13］。因此，在进行RAPC性能统计分析时应协同考虑各性能之间的影响，以确保分析结果更接近真实情况。将此次统计的RAPC各性能看作4个随机变量，并构成一个四维总体随机样本：

式中：C为抗压强度矩阵；S为劈拉强度矩阵；T为孔隙率矩阵；W为透水系数矩阵。

将每次获得的RAPC实测数据认为是对4个变量的一次观测，每一次观测得到一个样品值，即有：

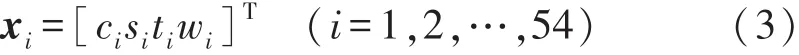
进而构成4×54的样本数据阵，记为

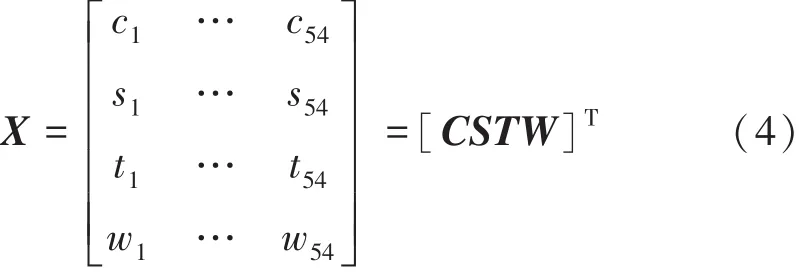
式（4）中，矩阵的行为观测次数，列为RAPC性能某一组实测值。

由上述统计结果可知，RAPC抗压强度、劈拉强度、孔隙率及透水系数基本符合正态分布规律。假设由RAPC各性能构成的四维随机样本符合多维正态分布规律，即样本数据阵X为四维正态分布随机变量，则X的联合分布函数为

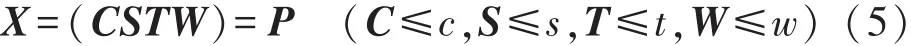
若存在某个函数f（c，s，t，w）对于任意实数均满足：

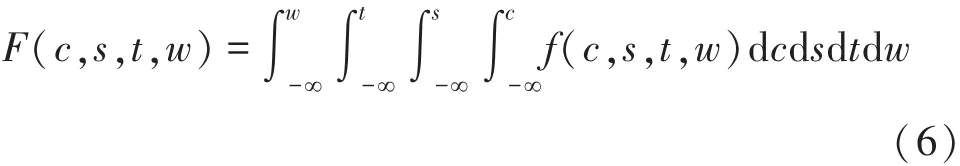
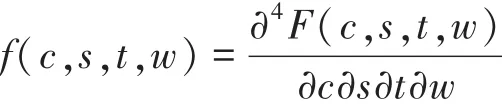
则称 f（c，s，t，w）为 X 的联合概率密度函数（简称联合密度函数）。则有：

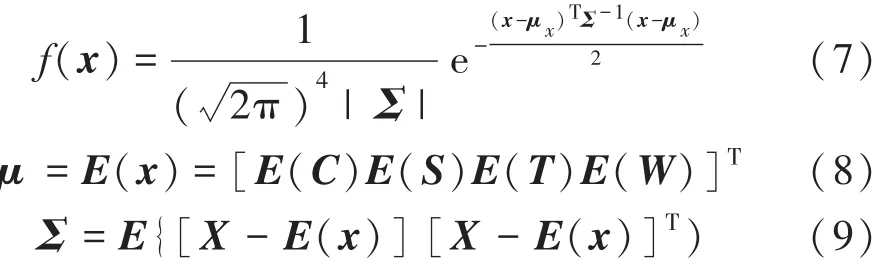
式中：μ为样本矩阵的均值向量；Σ为协方差矩阵。

3．2 均值向量及协方差阵估计

依据上述探讨并结合RAPC性能的实测数据，求得样本均值向量以及协方差阵，并无偏估计样本总体的均值向量和协方差。

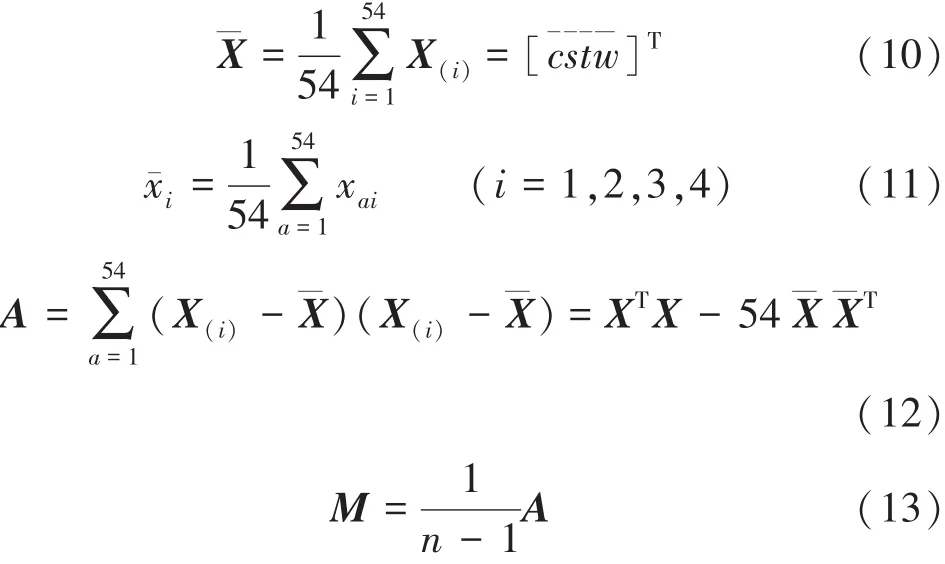
式中：¯X为RAPC各性能数据样本的均值向量；X（i）为54次中的某一次观测值；¯c、¯s、¯t、¯w分别为抗压强度、劈拉强度、孔隙率、透水系数的平均值；xai为总体矩阵内的元素；A为样本离差矩阵；M为样本协方差矩阵。

张校长介绍说，今年恰逢济南大学建校七十周年，近年来，学校着力增强高水平的创新能力，继续深度参与国家、地方创新体系建设，加快建立以需求为导向，创新为动力，协同为纽带，服务为目的的科技创新体系，努力在承担重大科技项目、产出重大科技成果和成果转化上实现新突破，在服务国家、地方经济和社会发展上作出新贡献。

依据式（10）～式（13），分别求得RAPC各性能数据的均值向量、离差矩阵以及协方差矩阵：

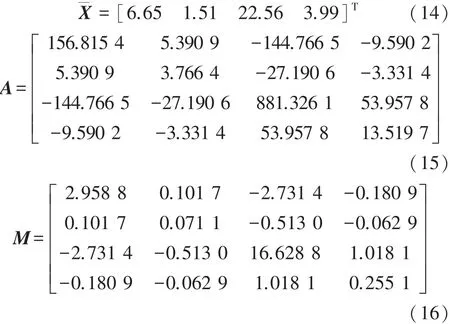
依据获得的协方差矩阵可以看出，RAPC各随机变量之间存在关联，将其样本数据的均值向量与协方差矩阵代入式（7），即可求得联合密度函数。

3．3 正态性检验

为了检验由RAPC各样本数据变量构成四元正态分布假设的正态性，选取较常用的多元正态性检验方法——χ2统计量的Q-Q图检验法。对于统计大于等于20组的数据而言［19-20］，该方法具有简单、易懂的特点，能够直观地展示检验结果。

（1）计算样品点 X（i）（i＝ 1，2，…，54）到 ¯X 的马氏距离

计算得到马氏距离并按大小排序：0．31、0．64、0．76、1．10、1．20、1．21、1．41、1．41、1．66、1．67、1．72、1．96、2．02、2．03、2．06、2．15、2．28、2．37、2．51、2．54、2．65、2．66、2．81、2．87、3．12、3．18、3．38、3．56、3．57、3．96、4．37、4．67、4．82、4．95、5．03、5．27、5．33、5．48、5．52、5．85、6．37、6．57、6．79、6．98、7．14、7．21、7．64、7．96、8．71、9．87、10．09、11．06、14．22、15．07。

（2）计算统计量D2的经验分布函数li及χ2分布的li分位数：

计算结果分别为：0．01、0．03、0．05、0．06、0．08、0．10、0．12、0．14、0．16、0．18、0．19、0．21、0．23、0．25、0．27、0．29、0．31、0．32、0．34、0．36、0．38、0．40、0．42、0．44、0．45、0．47、0．49、0．51、0．53、0．55、0．56、0．58、0．60、0．62、0．64、0．66、0．68、0．69、0．71、0．73、0．75、0．77、0．79、0．81、0．82、0．84、0．86、0．88、0．90、0．92、0．94、0．95、0．97、0．99。

（3）绘制χ2统计量的Q-Q图，如图4所示。由RAPC各性能实测数据计算得到的马氏距离和分位数构成散点，以其分布与直线（过原点且斜率为1）的重合程度判断是否接受正态性的假设［21］。由图4可以看出，除个别点略偏离直线外，其他均分布在直线上，说明由RAPC各随机变量组成的四维总体变量服从多维正态分布。

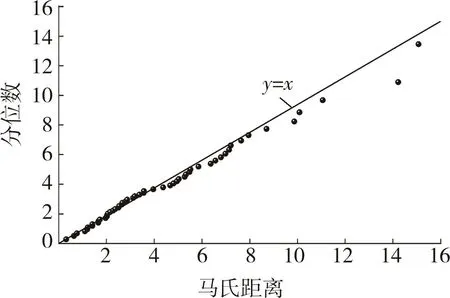
图4 χ2统计量的Q-Q图

4 结 论

（1）对试验获得的RAPC性能实测数据进行统计分析，结果显示各随机变量的均值、标准差及方差分别为 6．65 MPa、1．51 MPa、22．56%及 3．99 mm／s，1．74 MPa、0．29 MPa、3．72%及 0．50 mm／s，3．02 MPa、0．08 MPa、13．84%及 0．25 mm／s，且基本服从正态分布。

（2）依据RAPC各性能的统计分析结果，构建四维总体随机样本，通过计算得到其均值向量与协方差阵，认为RAPC各性能间存在关联关系。

（3）对RAPC四维总体样本进行基于χ2统计量的Q-Q图检验法的正态性检验，依据计算得到的马氏距离及分位数，确定RAPC各性能服从四维正态分布。