单臂试验连续型数据的贝叶斯Meta分析方法及实现

张天嵩

系统评价和Meta分析是循证医学重要的证据信息来源[1，2]，通过Meta分析对多个研究结果的统计综合被广泛用于评价不同干预的相对效应[3]。在牛津循证医学中心2011年发布的证据水平分级标准中，将以RCT为基础的系统评价作为评价某种干预措施受益或危害的1级水平[4]。虽然RCT是公认的最佳治疗性研究设计方案，但来自RCT的证据常缺乏或不足，难以回答所有临床问题，或有时RCT不需要、不可行或不恰当，如新药1期临床试验，则可以采用单臂试验设计方法[5，6]，国、内外均有依据单臂试验批准新药上市的案例[7]。所谓单臂试验是指将具有某种靶健康状况的个体样本给予试验性治疗并观察某种治疗效应的设计[6]，所有受试对象都在同一观察组，不设立其他实验组或对照组[5]。近年来，国内外循证医学工作者开始探索单臂试验数据的Meta分析方法。单臂试验的观察指标按资料性质可分为定量与定性资料。对于定性资料，多以比例、率、比数和发病密度等为效应量[5]，目前有众多研究文献介绍此类数据在贝叶斯和频率学框架下的Meta分析方法，以及基于R、Stata、SAS、RevMan等软件实现[5, 8-13]；而对连续型数据的Meta分析方法则研究或介绍不多，有少数介绍使用Stata软件[5]和Meta-Analyst软件[14]基于频率学框架下采用倒方差法进行Meta分析的文献，难以满足实践需要。本文介绍基于经典的正态-正态层次模型(NNHM)框架下单臂试验连续型数据的贝叶斯Meta分析方法，并通过实例来介绍R软件实现过程。

1 方法

1.1 研究数据 数据来源于2个Meta分析。数据1：来自Dai等的单臂试验的Meta分析文献[15]，主要观察来氟米特治疗银屑病性关节炎的有效性和安全性，本文选取的观察指标为银屑病皮损面积和严重度指数(PASI)评分，为治疗后评分与基线评分的变化值，具体数据信息为每个试验的样本量、评分均数及标准差，在表1中分别以“n”、“mean”和“sd”表示；数据2：来自Nagpal等的Meta分析文献[16]，主要观察造血干细胞疗法对卒中早期临床干预的有效性和安全性，该文献纳入了单臂试验和对照试验的数据，本文选取单臂试验的相关数据，观察指标为美国国立卫生研究院卒中量表(NIHSS)评分，为治疗后评分与基线评分的变化值，具体数据信息为评分的均数及其95%CI下限和上限，在表1中分别以“mean”、“ll”、“ul”表示。数据见表1。

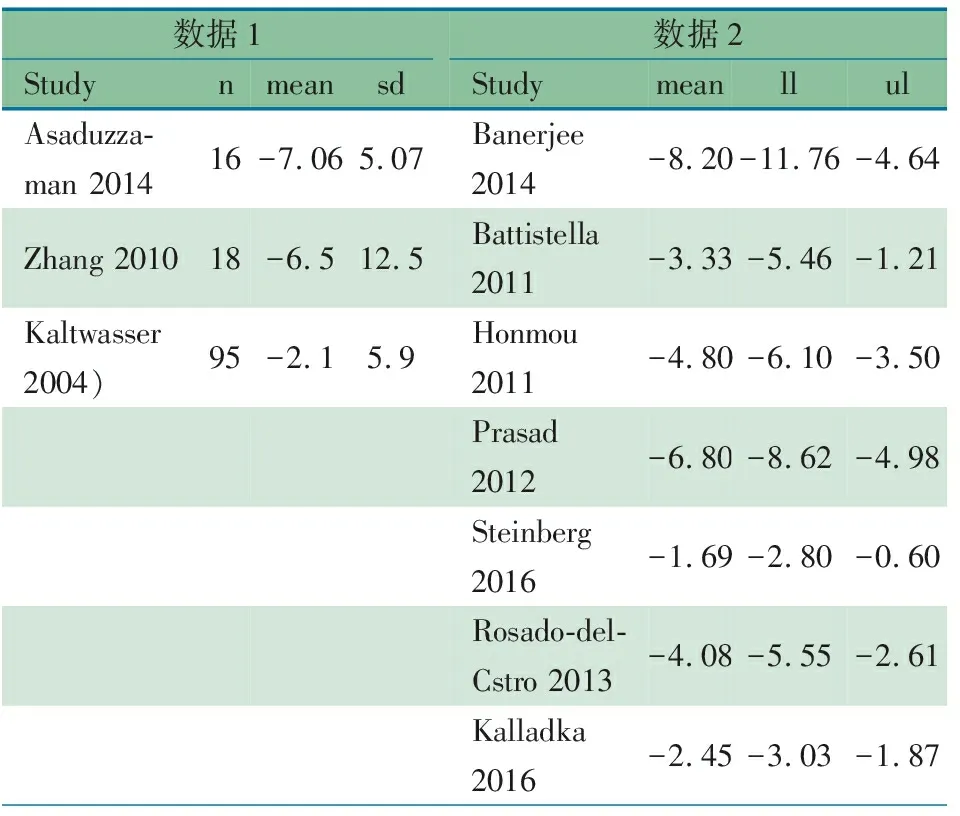
表1 分析数据

1.2 模型与方法 经典的Meta分析随机效应模型基于NNHM框架[17]：假设纳入Meta分析有i=1,…，N个独立研究，每个研究的真实值为θi，其估计值及估计值标准误分别为yi和Si，研究间真实效应变异为τ2，总的合并效应为μ，则模型有两层。

yi～N(θi，Si2)为抽样模型，假定yi服从未知均值θi和已知标准误Si的正态分布；θi～ N(μ,τ2)为参数模型，假定θi服从均数为μ、方差为τ2(标准差为τ)的正态分布，其中未知参数μ为主要感兴趣的参数，而异质性参数τ则一般被认为是讨厌参数。在频率学框架下，该模型可以使用Stata、R、SAS、RevMan等软件来拟合和实现，常用的参数估计方法有最大似然法(ML)和约束最大似然法(REML)等。在贝叶斯框架下，通常需要根据实际情况为参数μ和τ指定合理的先验。一般情况下，对于参数μ，指定为无信息先验分布；而对τ，可以指定为无信息先验分布如均匀分布，或弱信息先验分布如半正态分布等，该模型可由贝叶斯软件WinBugs等软件拟合。

1.3 模型拟合 在贝叶斯框架下，NNHM可由R软件(3.4.4版)的bayesmeta包的bayesmeta()函数来拟合[18]。在本研究中，参数μ设定为无信息先验μ～N(0，104)；参数τ指定为弱信息先验，分别为半正态(HN)先验和半柯西(HC)先验，尺度均设为1。以forestplot()函数绘制森林图。同时，为了比较与频率学框架下Meta分析结果，以metafor包的rma.uni()函数拟合该模型，选用REML法估计参数τ。具体代码及简要解释见表2。

表2 单臂试验连续型数据贝叶斯Meta分析代码(R软件)及简要解释

续表2 tau.prior=function(x){(dhalfcauchy(x, scale=1))})print(bma22)##绘制森林图forestplot(bma22)##拟合模型3:频率学框架,随机效应模型,采用REML法估计参数τ。meta23<-rma.uni(yi=score,sei=se,method="REML",data=stemcell)summary(meta23)

2 结果

2个研究数据贝叶斯和频率学Meta分析方法对效应参数μ和研究间异质性τ的估计结果如表3所示，2种方法获得参数μ点估计值有差异，95%CI宽度有明显的不同；参数τ估计值差异较大，基于HN(1)先验的贝叶斯方法似乎可以获得更为精确的估计值。需要指出的是，bayesmeta包提供了更多的贝叶斯分析结果信息，如在其“marginal posterior summary”结果显示部分，提供2个主要参数μ和τ后验众数、后验均数、后验中位数，及相应95%CI的下限和上限，为了与森林图结果一致，表1中所示选取的是后验中位数及95% CI的下限和上限结果。

数据1的森林图如图1和2所示。森林图中上半部分显示了纳入Meta分析的每个研究的效应量(即模型中的yi)的点估计及基于相应标准误获得的95%CI，以黑色表示，即森林图中的“quoted estimate”；以及每个研究真实效应参数(即模型中的θ_i)的点估计及95%CI,以灰色表示，即森林图中的“shrinkage estimate”；森林图底部显示合并效应量(平均值)点估计(后验中位数)和95%CI(与图中“mean”相应)，以及预测值及区间(与图中“prediction”相应)。

表3 基于NNHM框架下贝叶斯和频率学Meta分析结果

图1 数据1森林图[τ为HN(1)先验]图2 数据1森林图[τ为HC(1)先验]

3 讨论

单臂试验在医学研究中较为常见，如果其测量结局为连续型数据，则具有一个共同特征[19]：针对某一测量结局指标，除了干预实施后进行测量外，可能会对每一个参与者在干预实施前进行基线测量，因此可以获得最终测量值与基线测量值的差值，称为基线改变值或改变评分，所以系统评价者在Meta分析提取数据时可能会考虑同时提取基线改变值和最终测量值。对于连续型数据，原始研究对测量结果可能存在多种报告形式，常见的有：①测量指标均数及相应标准误(或方差)；②受试者样本量、测量指标均数及相应标准差；③测量指标的均数及95% CI；④测量指标的中位数及上下4分位数间距等；⑤测量指标的中位数、最大值及最小值等。无论何种形式的数据，只要最终能获得每个研究的效应量及其方差或标准误，即可进行Meta分析，一般可以通过2种途径：一是向原始文献的通讯作者发邮件索要原始数据；二是通过数据转换，具体方法可以参看国内外相关文献[19-23]。本文数据1已知样本量、测量指标均数及相应标准差，可以通过公式“均数标准误=标准差/样本量的平方根”获得均数标准误[24]；数据2(因文献[16]未报告每个研究的样本量，本研究聚焦在贝叶斯Meta分析方法介绍，简单处理为假定每个研究样本量很大，95%CI来自正态分布)已知测量指标95%CI，则可以通过公式“均数标准误=(95%CI上限-95%CI下限)/(2×1.96)”来获得均数标准误[19，22]，如果研究样本量小，或者95%CI由t分布计算所得，则上述公式中的1.96则需要一个更大一点t分布值代替[19，22]，该值可以用自由度(研究样本量-1)查t分布表或用Stata、R、Microsof Excel等软件计算获得。

一旦获得每个研究观察指标测量值及其相应标准误，则可以在NNHM框架下采用随机效应模型来进行Meta分析，主要有两个参数真实效应(real-valued effect)μ和异质性(heterogeneity)τ，如果异质性为0，则退变为固定效应模型。在NNHM框架下的分析方法有频率学和贝叶斯两大策略，目前更为常用的频率学策略一般分2步，第1步估计异质性，第2步基于异质性估计派生出效应估计，但目前有很多估计异质性算法，共同的问题是对于异质性方差分量估计易趋向于0，导致选择固定效应模型。贝叶斯策略近年来也已逐步应用于Meta分析中，综合了未知参数的部体信息、样本信息及先验信息，特别是可以允许(实际上也需要)指定先验信息用于数据计算。在贝叶斯随机效应模型中，根据需要很容易对效应参数μ指定为无信息先验或弱信息先验；对研究间异质性参数τ，则常需要根据效应量、研究数量等因素综合考虑指定为信息先验，特别是仅有几个研究纳入Meta分析时。有学者认为，除非在研究数量少或期望信息先验等情况下，一般均宜将τ指定为均匀分布；研究数量少时，推荐τ指定为重尾分布，如半学生t(half-Student-t)分布、HC分布、HN分布等弱信息先验[25,26]。本研究中所用数据纳入Meta分析的研究数量均较少，因此将τ的先验指定为HN(1),另指定HC(1)作为敏感性分析，以比较不同先验对参数估计的影响。本研究发现，采用贝叶斯分析方法，纳入Meta分析的研究数量较少(如3个研究时)，给定HN(1)和HC(1)先验，未知参数μ和τ的后验分布差异较大；而研究数量为中等(如7个时)，两个未知参数后验分布则较为接近，提示，Meta分析纳入研究数量少时，对于研究间异质性估计要谨慎，值得进一步研究和探索。

贝叶斯方法通常需要高维积分方法等，在计算方面较难实现，但随着现代计算机技术的出现和发展，特别是马尔可夫链蒙特卡洛(MCMC)方法的建立，使得计算方法制约问题得以解决，但使用MCMC方法需要一定量的专业知识如收敛性诊断和实践经验等。因在NNHM框架贝叶斯随机效应模型中，只有μ和τ两个未知参数需要估计和推断，可以利用数值积分方法或重要性抽样使计算简单化[27]，研发bayesmeta包的目的就是为了简单易行地实现基于NNHM框架下完全贝叶斯分析策略，采用称为散度限制性条件镶嵌(DIRECT)策略[28]的新算法获得未知参数的后验分布，使用者无需担心MCMC方法相关设置、诊断和后加工处理等贝叶斯方法专业问题。使用bayesmeta包可以快速获得精确的后验概括性结果，并能提供类似于经典频率学Meta分析森林图的图示化结果；后验分布可以准解析形式或预测估计和收缩估计(shrinkage estimation)等高级方法如存取。bayesmeta包还提供了其他结果信息，如预测未来一个新的研究真实效应参数θk+1值，即森林图中“prediction”相应部分，也可以通过summary()函数获得具体数字化结果。

最后，因为Bayesmeta包具有以下优点：①计算速度快，精确度和可重复性强；②操作简单，不需要深度掌握MCMC算法等专业知识；③允许快速敏感性检验、便捷地大规模模拟等，所以值得推广和使用。该软件包除了用于单臂试验连续型数据Meta分析外，还可以用于RCT等双臂设计的二分类数据、连续型数据、生存数据等贝叶斯Meta分析。