基于自适应差分进化算法的优化
2019-08-22李丽蓉王平
李丽蓉,王平
(1.山西警察学院 网络安全保卫系,山西 太原 030401;2.山西财经大学 资源环境学院,山西 太原 030006)
0 引言
差分进化(Differential Evolution,DE)算法是一种基于不同候选解集的优化算法。Storn和Price首先提出差分进化算法[1]。差分进化算法,作为进化算法中的一种,由许多候选解组成,候选解组成种群,并且种群经过一代代更新来发现最优解。差分进化算法与其他算法的不同处在于,每一个候选解自己不能寻找新的解,而是需要借助其他候选解的差异性来发现新的解。差分进化算法已经成功应用于各种领域解决不同现实问题,如电磁学、光学、模式识别和信号处理等[2-8]。差分进化算法目前已成为研究的热点并取得显著进展[9-13]。
差分进化算法主要利用获选解间的不同性来搜索更多的可能的解。一个候选解当作一个个体,每个个体的更新需要利用不同个体间的差异来进行。但是获取个体间的差异性的方式需要进一步的分析,以及怎么样利用这些差异性,即设置其相关的参数来搜索更好的解需进一步的研究。在现有的差分进化算法中,这些参数的改变导致其最终的结果变化很大。本文提出一种新的自适应技术,使其求解的性能比其他的自适应算法具有更好的鲁棒性。
1 差分进化算法
1.1 基本概念
差分进化的设计是基于一种随机、并行的搜索算法,运用了进化计算中的共同点,但是其需要的参数更少。标准的差分进化算法描述如下:
(1) 种群
(1)
(2)
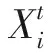
(2) 种群的初始化
(3)
这里xj,min和xj,max是其所求第j维的解的空间,rnd是一个随机数,其范围从0到1。
(3) 基于差异的组合
(4)
这里s1、s2、s3为随机整数,其范围从1到N,并且彼此不相等。不同变形版本的组合方法可以参考文献[14]。
(4) 交叉操作
交叉操作用来提高种群的多样性。最常见的交叉操作是均匀交叉,即
(5)
(5) 选择操作
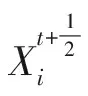
1.2 自适应差分进化方法分析
由于式(4)中F的改变而可能会导致无法发现全局最优解,相关的研究运用自适应策略来控制F,使其适应于不同的情况,从而避免F太大而易陷入局部最优解,太小而缺少足够的扰动来寻找新的解。
Dither DE (DDE)差分算法[15]被认为是最早之一的自适应差分进化算法。Karaboga和Ökdem也从事类似的研究工作[16]。在DDE中,自适应Fdither描述如式(6),其中Fmax和Fmin为F的最大值和最小值。Karaboga和Ökdem[16]用一个固定的随机数rnd来控制所有维数的F。文献[17]建议rnd控制每一维,而不是所有的维。
Fdither=Fmin+rnd×(Fmax-Fmin) .
(6)
Jitter DE (JDE)[15]采用一个随机因子来控制F的值,即
Fjitter=F×(1+δ×(rnd-0.5)) .
(7)
其中rnd是基于每维而不是一个固定的值对所有的维。JDE能对非欺骗性优化函数问题具有非常好的求解能力[14]。Fdither和Fjitter都引入了新的参数来控制F而导致需要优化新的参数值。在DDE中,Fmax和Fmin将会影响其寻找全局最优解的能力和其算法的收敛速度。而JDE需要求解函数的先验知识来设置参数δ,并且JDE对于目标欺骗性函数而言,难以找到最优解。
2 新的自适应策略
在自适应进化差分算法中引入新的参数将影响算法的收敛速度并且需要解决新的参数优化问题,为了避免此问题,本文提出了一种新的自适应策略来控制F,记为SinDE。这种新的自适应策略应满足以下约束条件:1)自适应化后的F必须是正数,扰动的方向仅由两个不同个体的差异来控制,这样利于往优化的解的空间搜索; 2)F必须是可变而不是固定的,适当的扰动利于发现不同新的个体;3)对F的控制不能引入新的参数,应该是非参数化自适应调制。根据以上约束条件,选择三角函数sin用来调制F,因为当输入的范围从0到π时,三角函数sin的值从0到1,能够满足这3个条件。Fsin定义如下:
Fsin=F×(sin(rnd×π)) ,
(8)
其中rnd是基于每维的随机数。
假设一个理想的自适应Fideal的范围是从0到1,对于DDE而言,Fmax=1和Fmin=0;对于JDE而言,当δ大于2的时候,F可能会小于0,而δ设置太小,F远远大于0,这需要合理的设置F和δ;然而本文提出的自适应方法,当F为1时即可满足条件。比较DDE、JDE和SinDE的自适应F的空间,可以得出Fdither和Fsin的空间宽于Fjitter的空间。进一步分析,Fdither和Fsin对于F的分布,Fsin的值绝大多数位于其中心位置,而Fdither则使F呈现为均匀分布,也就是说,在DDE算法中随机选择F,而SinDE算法中则是Fsin有针对性地选择F,这样的选择更符合数据分布特征。因此,本文提出的自适应算法将进一步提高收敛速度并且可以克服局部最优的问题。
3 仿真实验
3.1 实验设计
许多领域的问题都可以转化为求解全局最优化解,如工程设计、应用科学、分子生物学等[5]。许多全局最优解的问题经常包含有许多局部极优解,从而导致许多算法只能找到某个或多个局部解而无法发现最优解。本文采用一些经典的测试函数[18]来测试SinDE的算法性能,并和DDE、JDE和StdDE(表示直接用F而不经过自适应处理)算法进行比较。以上算法均由Matlab2017实现。
四个标准测试函数描述如下:
(1) Shpere
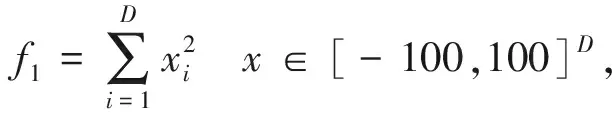
(9)
minf1=f1(0,…,0)=0 .
(2) Generalised Schwefel 2.26
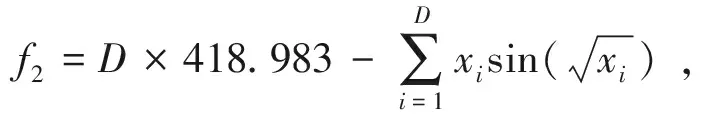
(10)
minf2=f2(420.968 7,…,420.968 7)=0 .
(3) Generalised Rastrigin
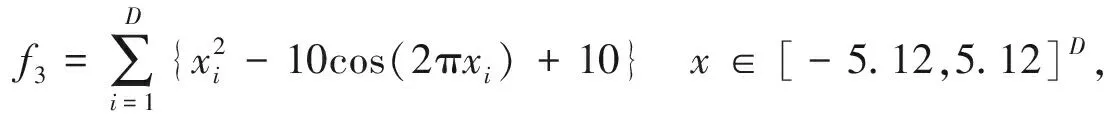
(11)
minf3=f3(0,…,0)=0 .
(4) Generalised Rosenbrock
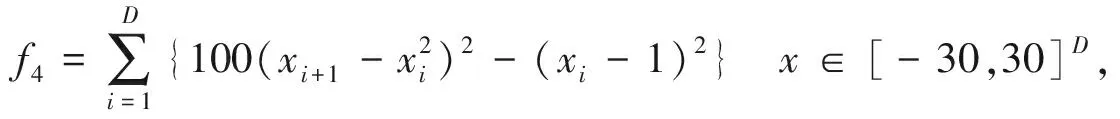
(12)
minf4=f4(1,…,1)=0 .
其中Generalised Schwefel’s Problem 2.26 (公式(10)) 的最优解的值被移到0, 其原公式为:
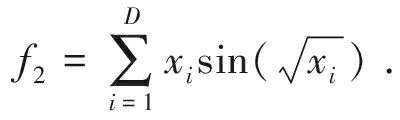
(13)
3.2 算法参数设置
为了比较这些算法的性能,在对这些函数优化问题的求解时,不同的参数应用于实验当中。这些参数主要包括F以及其相关的控制参数,种群大小N和交叉概率pcr。为了统计相关的函数评价次数,采用|fi(x)-minfi|<ε和有限的函数评价次数来判断相关的算法能否找到最优解,这里i=1,2,3,4。表1为其相关的参数设置。为确定算法鲁棒性,所有实验都独立运行30次,结果为平均值。
3.3 实验结果
表2为SinDE,StdDE,DDE和JDE基于不同F求解四个函数的最优解的平均值和方差。表格中“0”表示其相关的最优值满足终止条件,小于ε。对于函数f2,其原始最优值为-12 596.5 (30维),其ε一般都大于0.000 1。但是本文采用统一标准ε为0.000 1。从表2可得知,SinDE具有最好的鲁棒性。对于F的改变,其最优值变化的范围最小。对于函数f3,不同的F值没有影响SinDE找到最优解,而当F=1.5,StdDE,DDE和JDE都无法寻找到最优解。对于函数f4,所有的算法都无法寻找到最优解,但是不同的F值,SinDE所求解的最小值变化不大,都接近于最优值。而当F=1.5,StdDE,DDE和JDE都远离最优值。
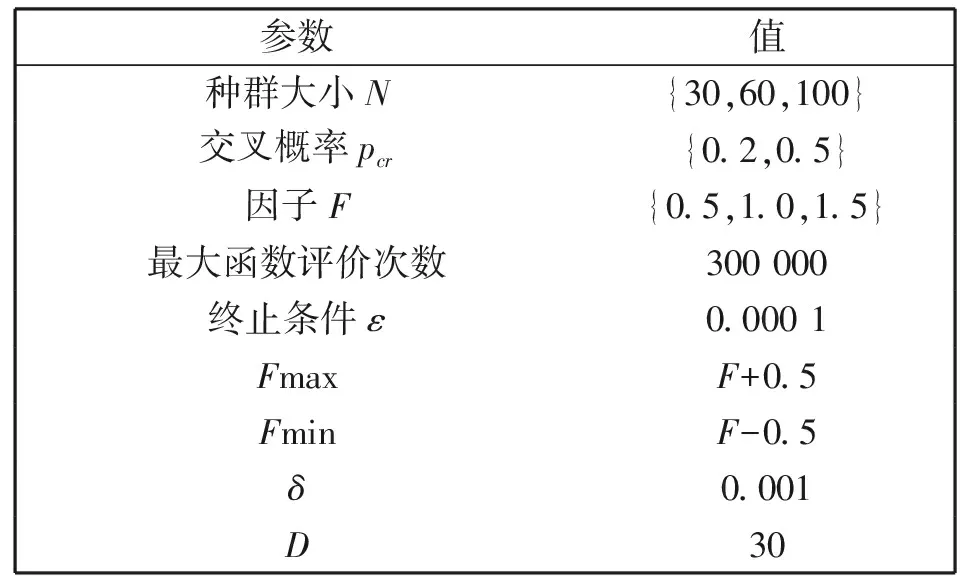
表1 参数设置
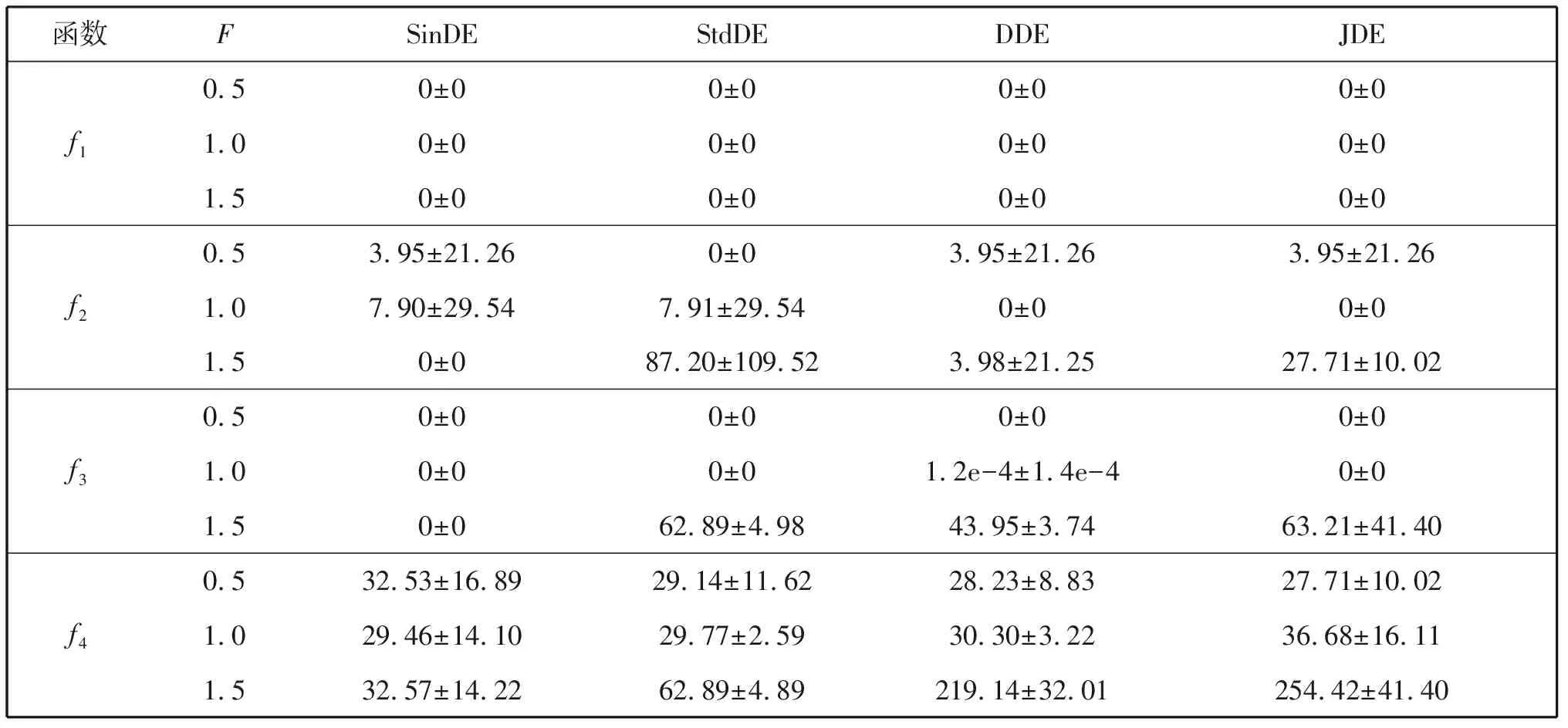
表2 四种算法最优解的平均值和方差(pcr=0.2,N=60)
表3为SinDE,StdDE,DDE和JDE基于这四个函数最优问题的函数评价次数的平均值和方差。其中“300 000±0”意味着在其300 000有限的函数评价次数内,相关的算法无法找到最优解。从函数f1,f2,f3可以看出,SinDE明显用最少的评价次数来寻找到最优解。
基于表2和表3的结果可以看出,当F变化时,SinDE比DDE和JDE更好地自适应调整F来寻找最优解。
表4为SinDE,StdDE,DDE和JDE求解四个函数的最优解的平均值和方差(pcr=0.5)。与表2比较,pcr=0.5差于pcr=0.2,其中当F为0.5时,DDE求解f2具有最优值,F为1.0时, StdDE和JDE求解f2具有最优值(两者平均值无显著性差异,基于显著性水平0.05的t-test),F为0.5时,StdDE和JDE求解f4有最优值。而对于其余结果,SinDE都表现为最优。特别当F为1.5时,针对f4的求解,StdDE,DDE和JDE无法寻找其解。由此可见,在交叉概率变化时,SinDE搜索这四个函数最优值的能力要优于DDE和JDE。
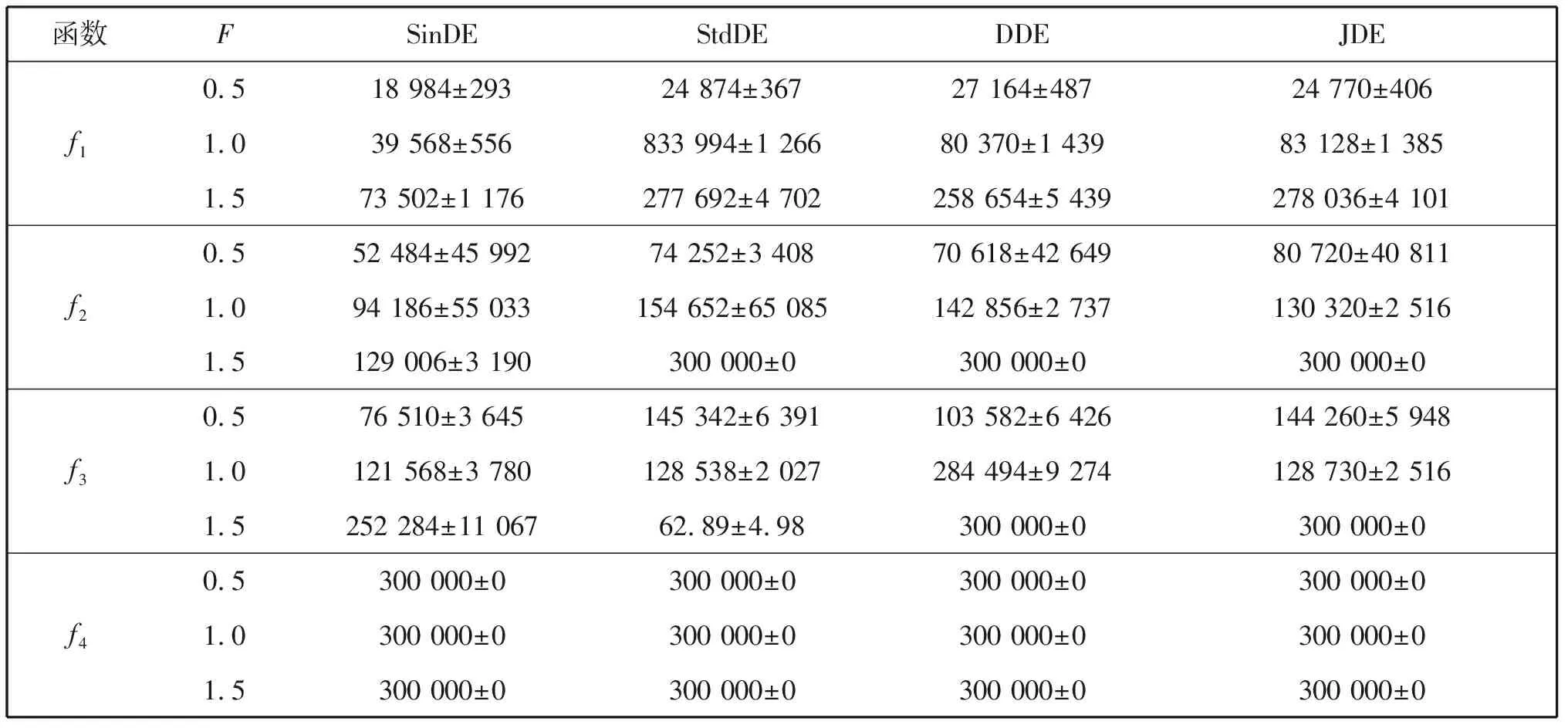
表3 四种算法函数评价次数的平均值和方差(pcr=0.2,N=60)
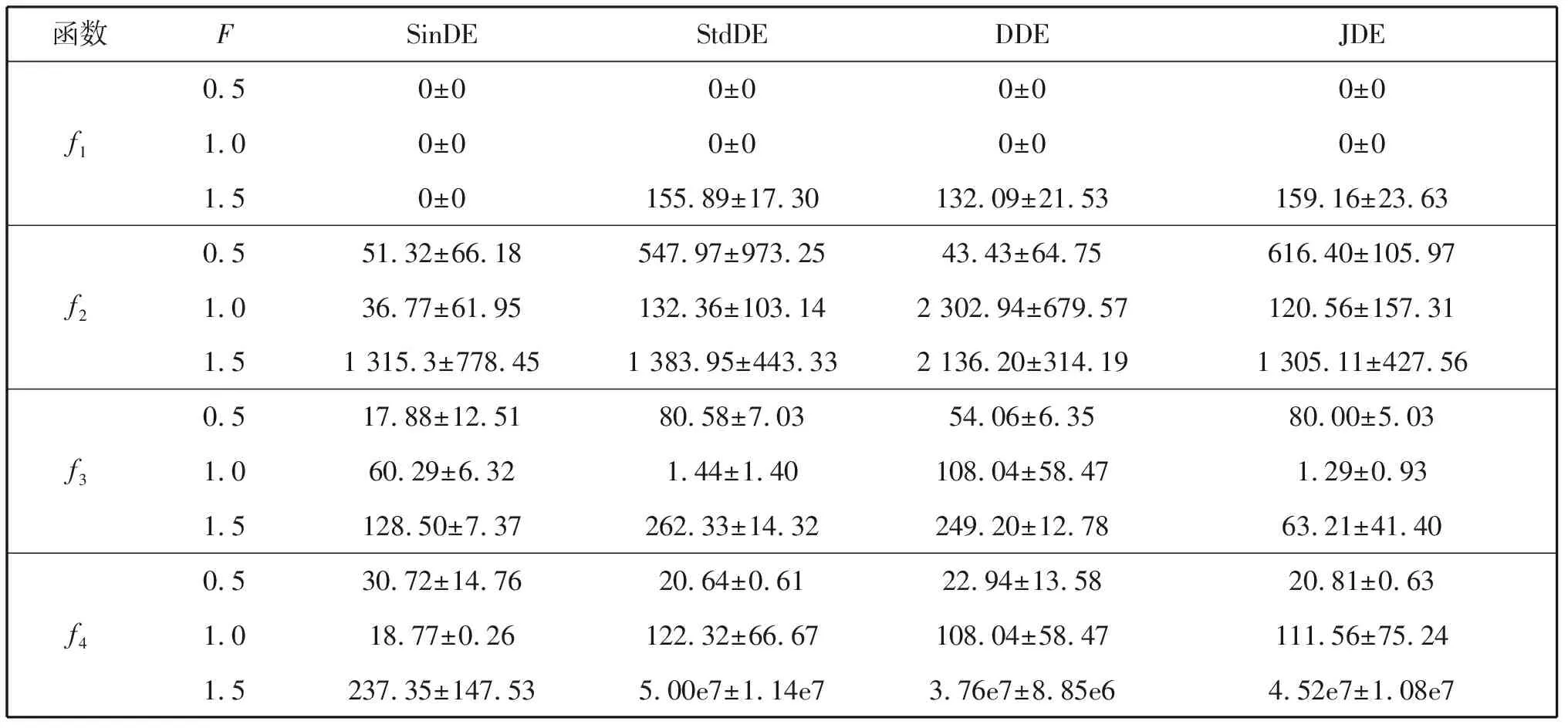
表4 四种算法最优解的平均值和方差(pcr=0.5,N=60)
图1和图2描述了这4种方法基于不同种群大小(N为30和100)的收敛状态,当N=30时,对于函数f1和f4,SinDE表现出了最好的收敛速度和搜索全局最优解的能力。对于函数f2,DDE的收敛速度要优于其他方法,但是SinDE的进化过程接近DDE。对于函数f3,DDE发现了全局最优解,而其他算法都收敛于用一个局部解。当N=100时,对于函数f1,f2和f4,SinDE明显要优于其他3种方法。对于函数f3,整体而言SinDE仍然优于其他的方法。对比求解函数f4的收敛情况,SinDE对其平均最小值的改变不大,但是StdDE、DDE和JDE用种群大小100求解的最小平均值要差于其用种群30求解的最小平均值。DDE在用种群大小100时,没有成功找到函数f3的全局最优解。从图1和图2可以看出,种群大小的变化对StdDE,DDE和JDE求解最优值有一定明显的影响,而SinDE所受的影响要低于其他3种算法,表现出一定的稳定性。
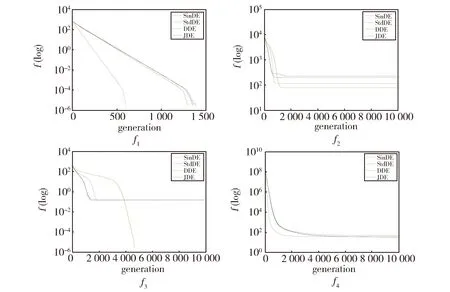
Fig.1 Evolutionary process of solve functions for four algorithms (N=30)图1 四种算法求解函数的进化过程(N=30)
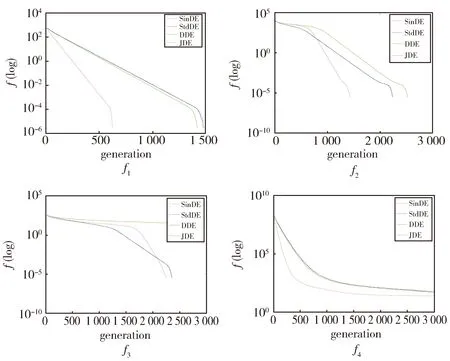
Fig.2 Evolutionary process of solve functions for four algorithms (N=100)图2 四种算法求解函数的进化过程(N=100)
4 结论
本文提出了一种新的自适应差分进化算法,可以自适应控制F因子。在标准函数的测试实验结果表明,相比于其他的自适应算法,本文算法表现出了非常好的求解函数最优值的能力,并且算法中的参数具有较好的鲁棒性。
在未来工作中,将在更多的数据集上验证本文算法,并且针对提出的自适应的3个条件,进一步研究更有效的自适应差分进化技术。
