风阻对矿井提升系统钢丝绳张力测量的影响
2019-08-22陈照业董明甫郭晓庆郭江涛张丹
陈照业,董明甫,郭晓庆,郭江涛,张丹
(新郑煤电有限公司, 河南 郑州 451100)
0 引言
多绳摩擦式提升机由多根钢丝绳共同承担罐笼的提升载荷。标准《煤矿安全规程》规定,在提升过程中,每根钢丝绳的张力值与平均张力值的差值不能超过±10%这一安全阈值[1]。如果超出此范围,就会形成安全隐患,若不能及时发现并处理,很可能会发生安全事故。因此,准确监测钢丝绳的张力对保障煤矿安全生产尤为重要。在煤矿生产过程中,为了降低井下空气中瓦斯和粉尘等有害物的含量,提高矿井生产的安全性,保持矿井内部与外界环境的良好通风效果是非常有必要的。通常情况下,矿井中设有通风口,通过矿井内部的风机加大井下的空气流动速度,以提高空气流动速率。对于立井而言,由于通风作用通常会导致井内风压与外界存在一定的压力差,部分空气会从提升井筒直接进入井下巷道,参与通风系统的空气循环。这部分由井筒进入井下的空气会作用在罐笼上,对提升罐笼造成一定的阻力效应,使得测量提升系统钢丝绳张力时混入部分外部干扰量,造成测量误差。
关于风阻对提升系统钢丝绳张力及载荷测量影响问题,国内外专家学者已进行过一定的研究。1987年,苏联科学家希尔什科夫[2]研究得出,不同材质和壁面粗糙度的罐道内的空气阻力情况不同,相应产生的层流和紊流作用也不相同。S. Kaczmarczyka, W. Ostachowicz等[3]研究了提升系统在风阻作用下钢丝绳的瞬态非线性振动特性,并指出系统中的不利动态行为在钢丝绳张力方面的具体影响。1984年,王良军[4]在对矿井提升机变位质量和矿井阻力进行测定时,提出计算矿井阻力系数时,需要考虑罐笼运行过程中的空气阻力,但并未给出具体分析。
由于外部干扰会直接影响钢丝绳张力及提升载荷监测结果,甚至在某些时间点会出现张力突变,导致系统内置报警及制动模块产生错误的制动及报警动作,不利于安全生产。因此,对干扰量进行分析对准确测量钢丝绳的张力、掌握钢丝绳的受力情况及提升载荷质量具有重要意义。
1 风阻对矿井提升系统钢丝绳张力测量值的影响
1.1 罐笼运行过程中井筒空气流场
矿井提升机罐笼在井筒中做往复运动时会受到空气阻力的作用,因罐笼在井筒中的运动类似于气缸中活塞的运动,故井筒中的气流会受到罐笼的挤压作用。由于罐笼两侧与井筒壁存在一定的空间,在罐笼运动时,罐笼周围的空气除少量层流运动外,还存在一定的紊流运动[5]。此外,罐笼在不同的运行速度下,其周围的空气流场也会呈现出不同的情况。以双罐笼在进风井筒中的运动为例,对不同速度下罐笼周围的空气流场进行分析,如图1所示。
图1中v0为不受罐笼运动影响的空气流动速度,vt罐笼的运行速度。根据运行中的罐笼与空气速度的关系,对图1中3种情况进行讨论。
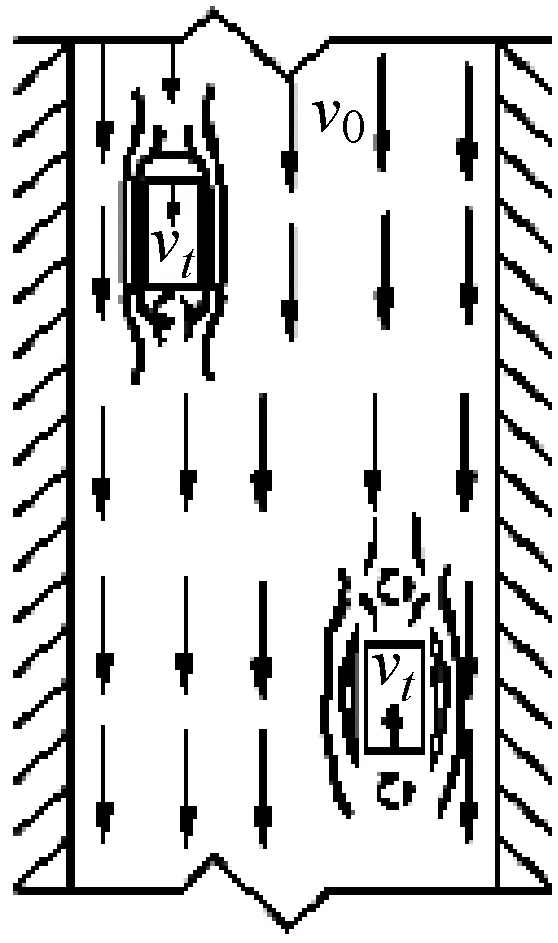
(a) vt
1)vt 2)vt=v0时,如图1(b)所示,井筒中罐笼做与风速同向且同速的运动,此时将罐笼看做井筒气流中的一个等速质点,井筒内的空气流动对其具体运动无影响。对于井底逆向上升的罐笼,其周围的空气流动情况同上,一般在矿井提升系统运行过程中,这种情况出现的概率相对较小而且时间短暂。 3)vt>v0时,如图1(c)所示,顺风运行的罐笼运行速度大于空气流动速度时,此时由于空气的黏性作用,罐笼四周的空气因受到黏性力的作用而被带着向前运动,罐笼顶、底面上的空气会形成紊流现象。逆向运动的罐笼周围也会出现前面所描述的空气绕流现象。 根据流体力学的相关知识,分析罐笼运行过程中井筒内空气的速度情况。为了使分析过程更加明了,首先对每个罐笼附近的空气速度场进行分析,然后再进行矢量叠加。井筒空气速度场如图2所示,图2中vw为罐笼运动压缩空气而产生的紊流运动的空气速度。 (a) 顺风罐(b) 逆风罐(c) 双罐笼叠加图2 罐笼运行时井筒的空气速度场 1) 顺风罐(v0与vt同向),如图2(a)所示。截面Ⅰ以上的空气受影响相对较小,可以认为符合管道中理想空气动力学的运动规律。罐笼顶部附近的截面Ⅰ处,由于空气紊流作用,使空气流动速度从v0加速到vt。相反地,罐笼底部附近的截面Ⅱ处,空气流动速度则从vt缓慢减速至v0。然后,空气以v0的速度运行,直至与另一个罐笼相遇。 2) 逆风罐(v0与vt反向),如图2(b)所示。截面Ⅲ以上空气流动情况与顺风时基本相同。在罐笼顶、底部附近,即截面Ⅳ、Ⅴ处,由于罐笼的运行方向与井筒中的空气流动方向是相反的,故会发生风速为vw的部分紊流空气。截面Ⅵ以下与截面Ⅱ情况相同。 3) 双罐笼叠加,如图2(c)所示。在提升系统运行过程中,会同时出现顺风罐和逆风罐两种情况,井筒中的空气流动情况较为复杂,而且气流的运动情况与罐的形状尺寸、运行方向和所处位置有很大的关系。在截面Ⅰ和截面Ⅱ之间的罐笼顶部和底部附近,由于空气紊流作用的存在会出现小范围的速度波峰。在截面Ⅱ、Ⅲ之间,由于两罐距离相对较远,故井筒中的空气仍以速度v0运动。在截面Ⅳ、Ⅴ(靠近逆风罐的顶、底部)处,由于空气紊流作用,会出现罐笼周围的局部空气做反向运动的情形。 罐笼在井筒中的运行速度一般为5~14 m/s,由于罐笼的运行速度一般大于风速,以图2(a)顺风罐为例,罐笼顶部会受到空气压力的作用即迎面阻力,这个力会对提升系统的张力测量造成干扰。同时,在罐笼的罐底会形成空气压缩波和紊流,这部分空气也会反作用于罐笼,产生相应的壁面摩擦力以及紊流阻力,造成提升载荷称重误差。 根据提升系统的不同提升阶段对井筒风阻进行讨论,即提升系统启动匀加速阶段、匀速运行阶段、匀减速阶段。 1.3.1 提升系统启动匀加速阶段罐笼风阻分析 图3所示为加速运行时井筒中的罐笼位置及其周围的风速情况。当提升系统处于启动加速阶段时,两提升罐笼分别从井口或井底初始位置运动。假设A罐位于井口位置,在提升钢丝绳的作用下顺风运行,A罐受到井内空气的迎面阻力FA、环状空间中空气黏性作用产生的罐笼壁面黏性摩擦阻力fA作用,由于此时罐笼运行速度较慢且运行方向与风速方向一致,故此处空气紊流阻力忽略不计。对于位于井底的B罐,在提升过程中,罐笼不仅会受到井筒空气的迎面阻力FB、壁面黏性摩擦阻力fB作用,由于罐笼的运行方向与空气的流动方向相反,还会受到上升过程中的空气紊流阻力fBw的作用。 (a) 匀加速罐笼运行位置(b) 风速分布图3 匀加速时罐笼所受风阻 根据流体力学相关知识,A罐所受外部空气的迎面阻力为: (1) 式中:ρA为空气密度,取标准大气压下的空气密度1.293 kg/m3;CP为压差阻力系数,通常为0.75~0.95;SA为井筒中A罐的迎风面积,m2。 A罐在环状空间中由于空气黏性作用而产生的壁面黏性摩擦阻力为: (2) 井底处的B罐做与风速相反地提升运动,B罐所受到的空气迎面阻力为: (3) 式中:SB为B罐的迎风面积,m2。 B罐在环状空间中由于空气黏性作用而产生的壁面黏性摩擦阻力为: (4) 式中:BB、LB为B罐对应的尺寸。 B罐因空气紊流作用所受到的空气阻力为: (5) 通过对提升系统初始运行阶段A、B罐笼受到的迎面阻力、黏性摩擦阻力以及紊流阻力进行理论计算,结合井筒中空气的速度场,对两个罐笼而言,空气迎面阻力和黏性摩擦阻力均导致提升系统钢丝绳张力增大,故取正值。而B罐受到空气紊流的作用减小了提升机钢丝绳的张力,故取负值。由此可以得到提升系统A、B罐笼钢丝绳张力的变化量为: (6) (7) 1.3.2 提升系统匀速阶段罐笼风阻分析 随着系统提升过程的进行,罐笼逐渐达到最大运行速度,然后以该速度匀速运行。假设匀速运行阶段出现在图4(a)所示位置,结合图1(b)井筒中双提升罐笼空气流场分布情况,对两罐笼所受空气阻力情况进行分析。对于顺风罐笼,可将其看做一个风流中等速运动的质量体,由于此时罐笼运行速度达到最大值,因此还需要考虑运行罐笼对空气的压缩作用,故A罐除了受到稳定的空气迎面阻力、壁面黏性摩擦阻力作用,还受到空气紊流阻力fAw作用。由于此时空气流动速度及罐笼运行速度为固定值,在不考虑罐道摩擦作用的情况下,空气阻力在匀速运行过程中始终维持某一稳定值。对于逆风罐笼而言,其风阻变化情况基本与顺风罐笼类似。 (a) 匀速罐笼运行位置(b) 风速分布图4 匀速运行阶段罐笼所受风阻 A罐的迎面空气阻力FA、壁面摩擦阻力fA与前文计算方法相同。A罐因空气紊流作用所受到的空气阻力为: (8) 综上所述,此时A罐钢丝绳张力的变化量为: (9) 逆风罐笼同样受到空气的迎面阻力、壁面摩擦阻力以及紊流阻力,其对应的张力变化量方程与式(7)相同。 1.3.3 提升系统匀减速阶段罐笼风阻分析 提升过程中会出现一段时间的匀减速运行状态,此时提升速度随着时间不断降低。在匀减速运行状态下,井筒中空气流动情况与前文描述匀加速的情况类似,此时罐笼位置以及风速分布情况如图5所示。随着提升速度不断减小,对应的空气紊流作用也在不断减小。对于顺风罐笼A,匀减速运行阶段A罐钢丝绳的张力变化量与式(9)相同;对于逆风罐笼B,钢丝绳的张力变化量与式(7)相同。 (a) 匀减速罐笼运行位置(b) 风速分布图5 匀减速运行阶段罐笼所受风阻 由于季节的变化或井下瓦斯及粉尘含量的不同,井中风机的运转速度不同,故井筒中的空气流动速度不是固定不变的。现根据前文所建立的空气阻力的力学方程,对风速为3.8 m/s、5.95 m/s和6.7 m/s 3种情况进行分析。 图6~图8分别对应井筒中的运行风速为3.8 m/s、5.95 m/s、6.7 m/s时,不同提升阶段下降与提升罐笼的风阻变化情况。由仿真结果看出,罐笼所受风阻的大小与提升速度、运行方向及空气流动速度等因素有关。 1) 风阻变化量与提升系统的提升速度有关。分析某一风速下下降罐和提升罐风阻变化曲线可知,匀加速及匀减速阶段罐笼所受空气阻力是不断变化的。匀速运动时,由于空气流动速度与罐笼运行速度均保持不变,因此风阻的变化量也稳定在某一固定值。当井筒中的风速为3.8 m/s时(即空气流动速度小于最大提升速度),顺风罐笼所受空气阻力先逐渐减小,当提升速度等于风速时风阻最小,此时罐笼可等价于流动空气中的质点,此后随着提升速度继续增大,风阻又随之增大,当提升系统匀速运行时,风阻值保持不变。对于逆风罐笼,随着提升速度的增大,风阻逐渐增大,风阻最大值对应提升速度最大值,然后随着提升速度的降低,风阻随之减小。当井筒中的风速为5.95 m/s时(即空气流动速度等于最大提升速度),对于顺风罐笼,风阻先随着提升速度增大而减小,然后保持恒定,再随速度的减小而增大,最后在爬行阶段保持稳定。逆风罐笼的风阻变化情况与风速为3.8 m/s时相似。当井筒中的运行风速为6.7 m/s时(即空气流动速度大于最大提升速度),风阻的变化曲线与风速为5.95 m/s时类似。 (a) 下降罐笼风阻 (b) 上升罐笼风阻图6 井筒进风风速为3.8 m/s时空气阻力 (a) 下降罐笼风阻 (b) 上升罐笼风阻图7 井筒进风风速为5.95 m/s时空气阻力 (a) 下降罐笼风阻 (b) 上升罐笼风阻图8 井筒进风风速为6.7 m/s时空气阻力 2) 风阻变化量与罐笼的运行方向有关。分析同一风速下提升罐和下降罐的风阻变化情况:对于顺风罐其风阻变化情况先缓慢下降,然后在阻力最低值处保持一段时间,接着缓慢上升,再保持某一恒定值,最后出现少量的突变。对于逆风罐笼风阻的变化趋势与顺风罐笼的总体趋势相反。 3) 风阻变化量与井筒空气流动速度有关。对比图6、图7和图8下降(顺风)罐或上升(逆风)罐的风阻变化情况可以看出,当罐笼处于同一运行状态时,井筒中空气流动的速度越大,其所受风阻越大。风速的变化对风阻的变化趋势影响不大,其作用结果直接反馈于风阻幅值。 在载荷测量时可根据风阻的变化量对提升载荷进行实时补偿,以达到消除误差、准确测量的目的。 为了验证上述分析的正确性,首先利用张力监测系统对提升系统钢丝绳张力进行测量,然后在上位机中编写程序对测量值进行张力补偿。监测系统使用数据采集卡及便携式笔记本电脑进行数据采集和存储。压块传感器通过电缆与压力变送器相连接,压力变送器将传感器所测得的压力信号做放大处理,然后传入数据采集卡,数据采集卡通过USB线与便携式笔记本电脑相连接。压块传感器通过+12 V锂电池供电。监测系统的结构如图9所示。 图9 钢丝绳张力监测系统 图10和图11分别为无载荷及有载荷两种状态下提升系统的理论张力、实测张力及补偿张力随时间变化的曲线。其中补偿张力曲线为对提升过程中风阻这一张力干扰量进行补偿后得到的曲线。从图中可以看出,随着提升系统的运行,上升罐笼的钢丝绳张力呈增大趋势,下降罐笼的钢丝绳张力变化趋势则相反,提升系统匀速运行阶段钢丝绳张力值呈现规则变化,在加速启动或减速停车期间由于提升工况相对复杂,张力波动情况也比较复杂。 (a) 罐笼提升绳端载荷 (b) 罐笼下降绳端载荷图10 未提升重物时钢丝绳理论、实测及补偿后的张力曲线 (a) 罐笼提升绳端载荷 (b) 罐笼下降绳端载荷图11 提升重物时钢丝绳理论、实测及补偿后的张力曲线 通过对比可以看出,虽然同一工况下3条张力曲线波动量情况仍存在一定的误差,但总体变化趋势基本一致,张力补偿曲线比实际测量情况效果更好,更加贴近理论值,且基本在理论值处做规律性的上下波动。因此,本文分析的关于风阻的理论计算能够真实有效地反应提升过程中空气阻力对钢丝绳张力测量造成的干扰,验证了补偿张力干扰量这一方法的可行性。 本文研究了井筒风阻对提升机钢丝绳张力测量及载荷监测的干扰情况。基于流体力学理论,结合提升系统提升时罐笼的运行特性,从罐笼所受迎面阻力、壁面摩擦以及紊流阻力3个方面分析了风阻的作用规律,并对风阻导致的钢丝绳张力干扰量进行了数值仿真。最后对现场所测得的结果进行张力补偿,通过与理论值的对比,验证了风阻模型的正确性以及张力补偿方法对提高钢丝绳张力及载荷监测统精度的有效性。1.2 罐笼运行过程中井筒空气速度场

1.3 提升过程中罐笼的空气动态阻力
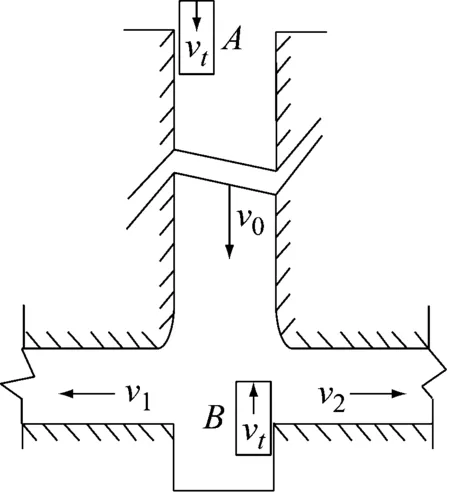


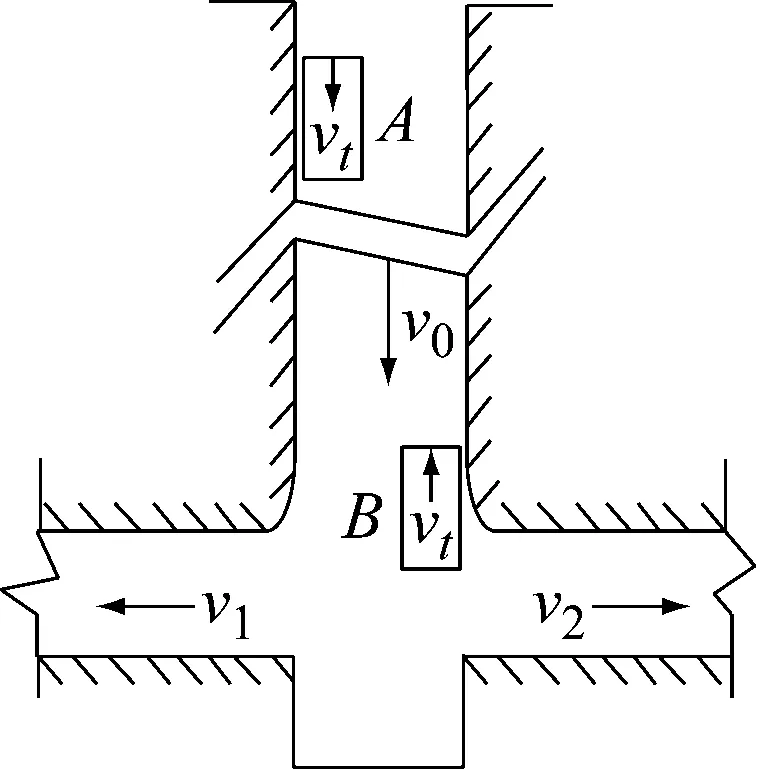
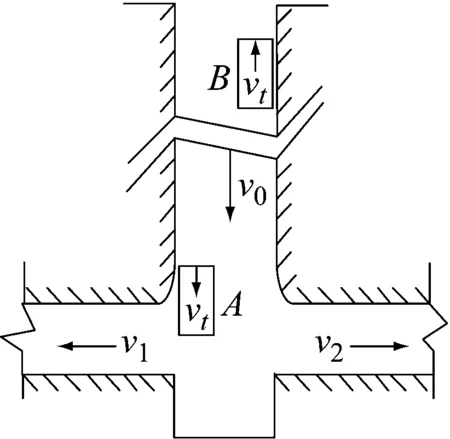
2 空气阻力的动力学仿真分析
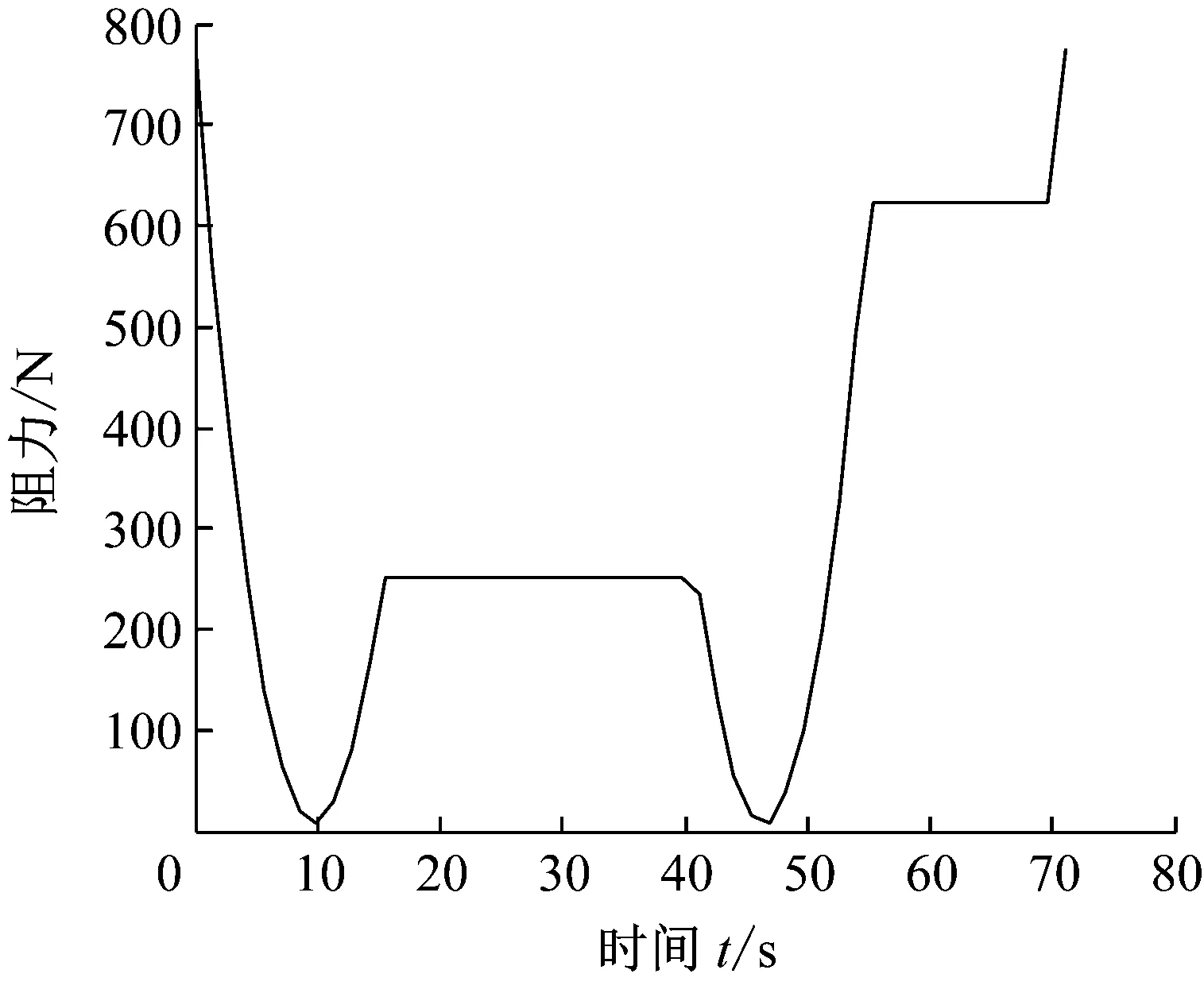
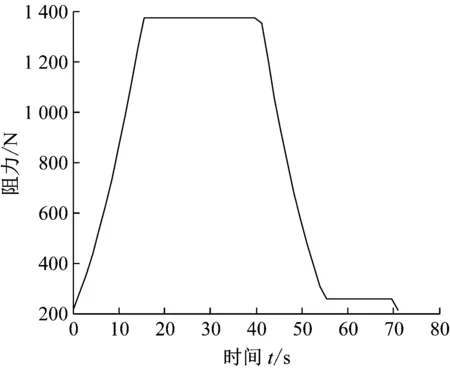


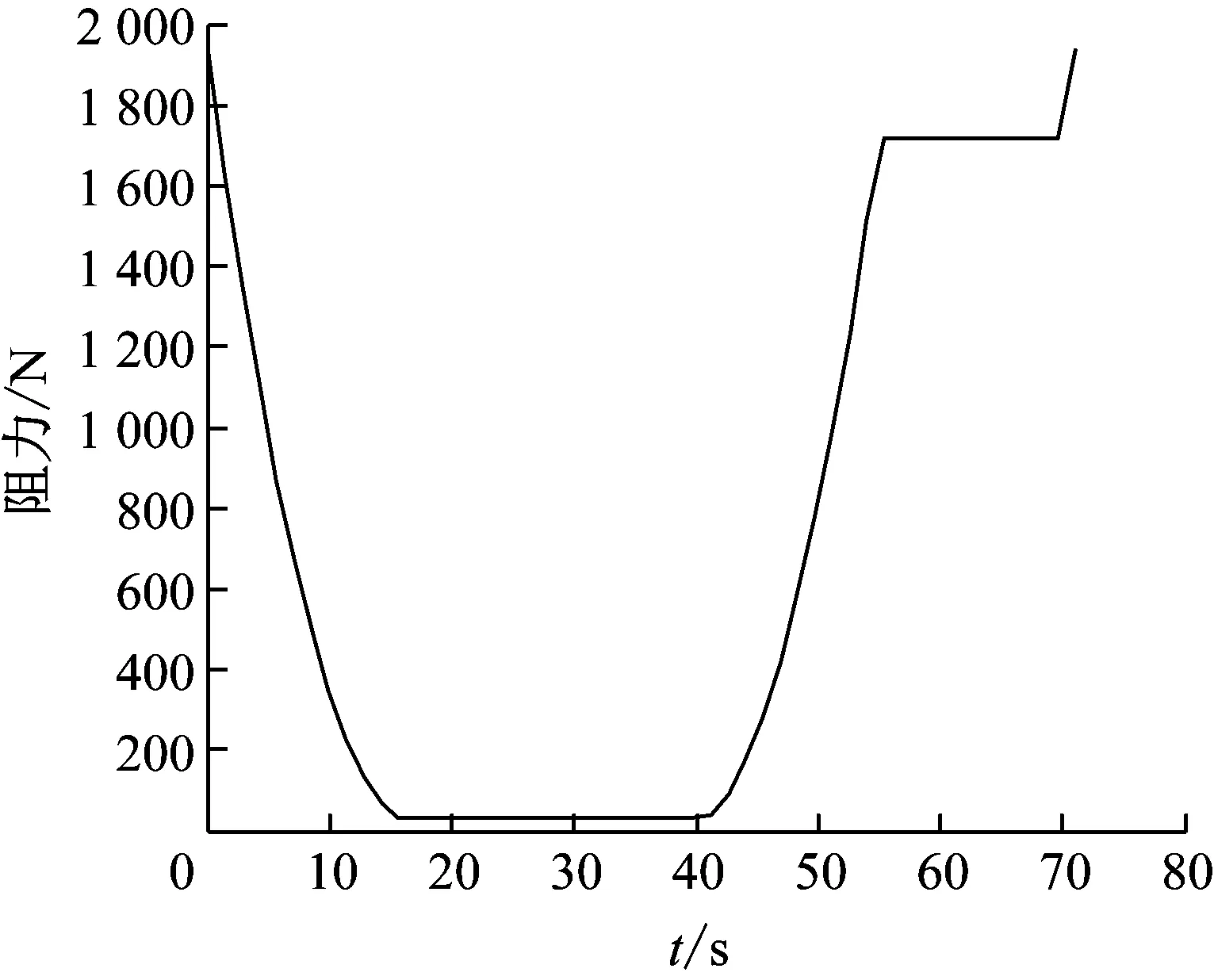

3 风阻作用下钢丝绳张力干扰量实验验证



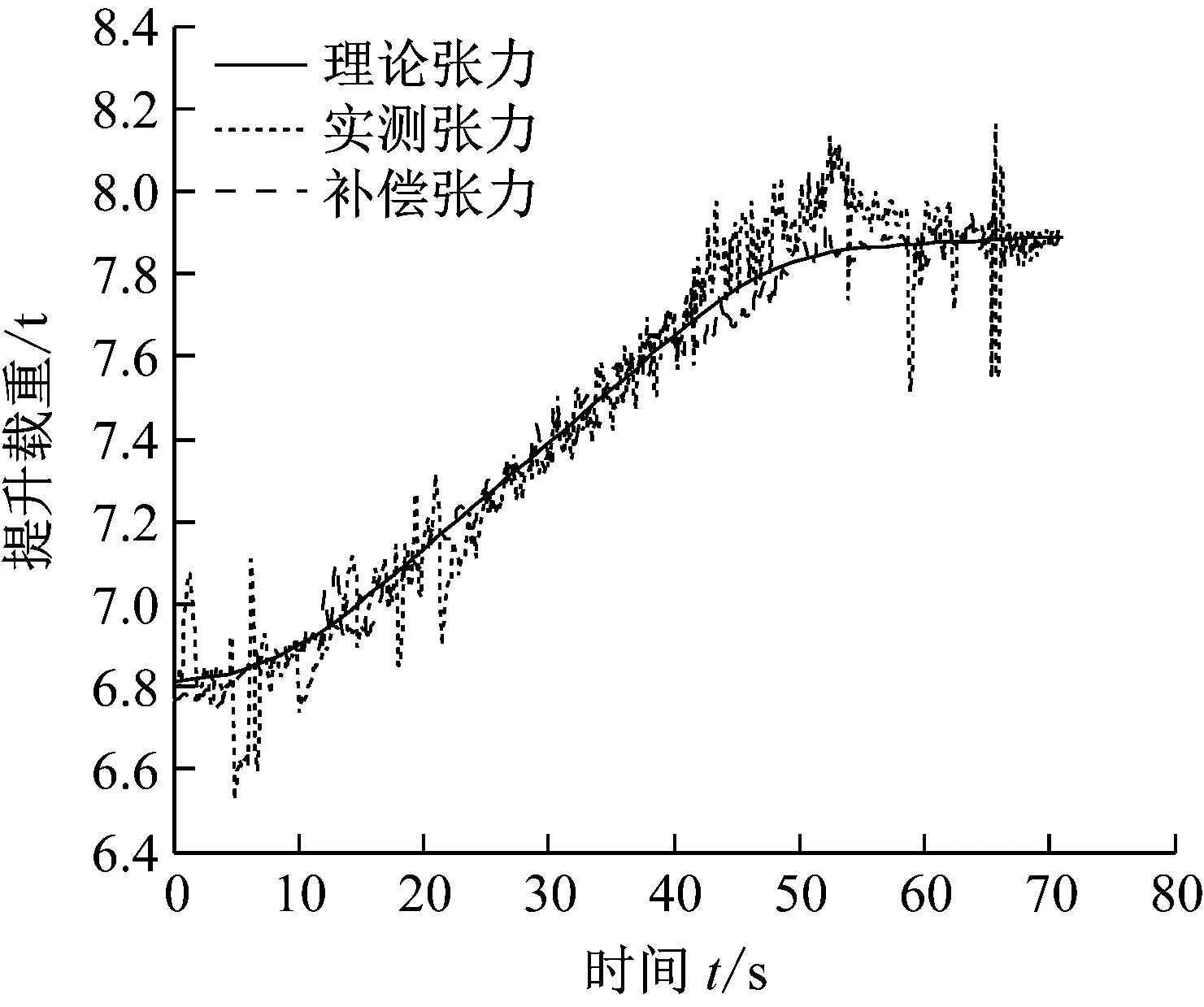

4 结论
