基于机器学习的高速列车转向架振动信号监测

蔡俊鹏，吴炳福，陈德旺

(1.福州大学 数学与计算机科学学院，福建 福州 350116；2.福州大学 轨道交通研究院，福建 福州 350116)

0 引 言

中国高速铁路具有高速度、高密度和大载客量等特点，这些指标都体现了中国高速铁路的综合水平已经达到了世界前列。中国高速铁路运营最高速度已经达到了350公里每小时，保持着高速铁路历史最高运营速度的记录。在列车运行中，列车转向架是高速列车的重要部件，在长期的运营中保存了大量的转向架振动信号数据，其振动信号很大程度上决定车辆运行的稳定性和安全性。经实验表明，对转向架振动信号提取的特征进行监测与分析能够准确识别出列车故障的状态，识别率高达92%[1]。随着高速列车运营里程的增长，转向架的服役性能与安全状态始终处于时变状态，这对转向架的安全与维护带来极大的挑战。因此准确地分析转向架的振动数据信号，能有效指导高速列车的安全提速，优化转向架的镟修周期，有利于缓解中国高速铁路运营和交通运输的压力，提高中国高速铁路的运营竞争力，是一个重大而有意义的课题[2-3]，对高速列车运行的经济性和安全性都具有重要意义。

在转向架部件研究方面，国内外科研工作人员在监控技术的基础上，使用增强实验仿真的方式，以不同的方法对转向架的故障检测诊断问题进行了深入研究，并取得了许多成果。例如，金炜东等[4]对转向架故障数据进行分类训练，训练模型的准确率达到了90%以上。秦娜等[5-6]采用集合经验模态分解EEMD对列车振动信号进行分析，进一步提高了支持向量机的转向架故障特征的识别率。侯亚东等[7-8]采用小波变换处理转向架齿轮故障监测信号。Hinton等[9-10]基于人脑学习思想提出深度学习的机器学习方法，Dahl等[11]验证了基于深度学习方法训练转向架故障功率谱数据的可行性。庞荣等[12]利用深度学习的方法对转向架的故障特征提取，对其中关键部件的识别正确率有了很大的提升。总的来说，目前国内外对转向架的研究方案都有其理论和实际意义，但是也存在一定的缺陷。基于故障诊断的方法，基于研究现代信号处理方法(EEMD、Hilbert变换等)和数据挖掘分类算法(支持向量机、K最近邻、隐马尔可夫模型等)[13-15]的研究方法，能有效对转向架故障进行诊断，提高维修效率。但是这些方法都采用增强实验的方法来研究，存在实验成本高、难验证的问题。而且增强实验与实际相比存在性能偏离，实际中的转向架结构参数是缓慢变化的。因此，文中以动车长期运行过程当中保存下来的转向架振动信号为基础，对其分析研究，该方法不存在发生性能偏离和数据量不足等缺点，实验结果更加契合实际运行情况，且实验成本低，能真实反映转向架的服役性能变化规律，具有较好的指导意义。

文中分析对比了国内外关于转向架的研究现况，以实际动车运营数据作为主要研究对象，对复杂的转向架振动信号数据进行小波变换去噪处理。在此基础上，研究转向架部件的振动速度、振动加速度和历史运营里程与振动值的服役性能规律，通过对多元线性回归、反向传播神经网络、径向基函数神经网络、回归决策树和随机森林算法实验进行对比分析，最终得出随机森林算法在动车转向架振动数据的信号监测中精度最优。验证了基于随机森林算法的高速列车转向架振动信号的研究在转向架服役性能和安全运行方面起到有效实时监测的效果，具有一定的研究价值。

1 转向架振动信号数据

文中的转向架数据集是通过专业的轨道交通车辆安全监测系统对运营动车的长期跟踪，实验采集得到的。数据集包括5个转向架关键部件：枕梁、轴箱、构架、弹簧筒和冷却风机。这些数据集包含了部件的横向振动有效值、横向振动最大值、垂向振动有效值、垂向横向振动最大值和高速列车运营速度、运营加速度、历史运营里程等信息。经过实验得知，转向架其余部件的实验结果对比分析过程与枕梁相类似，并且实验结果所采用的模型与枕梁是一致的，为了避免篇幅冗余，文中以枕梁数据为例进行实验分析。

动车转向架枕梁垂向振动中的训练集共有18 370个训练样本，囊括了6种不同的历史运营里程的样本，其中11.7万公里的样本3 433个，15万公里的的样本2 889个，20万公里的样本2 947个，25万公里的样本2 908个，30万公里的样本3 092个，35万公里的样本3 101个，每种运营里程下的数据记录着转向架枕梁运营过程中的振动有效值和振动最大值随运营速度、运营加速度的变化关系。

图1是11.7万公里运营里程下动车转向架枕梁垂向振动有效值和振动最大值的数据。

图2是在不同历史运营里程下列车从启动到加速到最大速度的转向架枕梁垂向振动最大值和振动有效值的平均值数据。

无论从单个历史运营里程还是从多个历史运营里程分析，该动车转向架振动信号随着运营里程和时间的增长，其振动值上升均具有一定的规律。由于转向架的振动的信号十分复杂，其信号频谱宽大，存在近似于白噪声的干扰噪声频谱几乎覆盖了整个振动信号阈值，很难确定信号的滤波频率，且转向架振动信号中夹杂着大量的随机噪声，无法严格按周期对数据进行采样。转向架振动激励源多，转向架的某个部件的振动信号数据往往会与大量的随机噪声数据相互影响，导致各种振动数据的信噪比特别低[16]。为了提升原始信号信噪比及样本数据曲线光滑度，需要对数据进行去噪处理。

图1 11.7万公里运营里程振动散点图

图2 不同运营里程的振动平均值

2 基于小波变换的转向架数据去噪

数据的去噪滤波是信号数据处理领域中一个重要的组成部分[17]。数据去噪的方法有很多种，但是有些去噪方法会过度的平滑，造成谱线中的峰值失真，从而丢失信号的重要信息成分。为了得到更高的信噪比，通过仿真实验，对几种常用的滤波去噪方法(包括巴特沃斯低通滤波器去噪、FIR低通滤波器去噪、移动平均滤波去噪、小波去噪等)进行滤波前后的波形图片分析对比。从小波去噪的结果来看，由于小波去噪能自动适应时频信号分析的要求，得到波形不是很平滑，但是去噪效果明显，且上升沿和下降沿保持的非常高，对于转向架数据信号的演变规律的信息得到了较好的保存，相比之下，它很好地解决了巴特沃斯低通滤波器和FIR低通滤波器无法刻画信号的非平稳特性，信噪比低的缺点。因此，最终选定小波变换对数据信号进行去噪。

小波变换(wavelet transform，WT)是近年来十分热门的去噪分析方法，它是短时傅里叶变换局部化思想的继承和发展，对含有等效噪声或人为噪声有很好的分割效果[18]，并且克服了窗口大小不随频率变化和缺乏离散正交性等缺点，是进行信号时频分析和数据处理的理想方法[19]。它的主要优点是通过对时间频率的局部化分析，伸缩平移运算对信号逐步进行多尺度细化，最终达到高频处时间细分，低频处频率细分，从而充分突出问题某些方面的特征，自动适应时频信号分析的要求。

文中对11.7万公里运营里程下列车从启动到加速到最大速度的转向架枕梁垂向振动有效值和振动最大值的数据进行小波去噪处理，所选数据的小波去噪滤波器分解层数为两层，选择阈值方法为rigorsure方式，选择软阈值去噪，噪声结构为unscaled white noise，可以给出小波去噪滤波器的运行结果，如图3所示。

结果表明，去噪效果明显，能自动适应时频信号分析的要求，且上升沿和下降沿保持的非常高，没有过度平滑而造成振动信号线谱峰值失真，对于转向架数据信号振动规律的信息得到了较好的保存，可以得到较高的振动信号的信噪比。

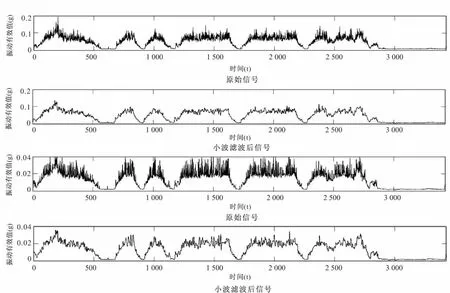
图3 小波变换去噪结果

3 基于机器学习的转向架振动信号的比较分析

在转向架系统中，其参数包括速度、加速度和历史运营里程，其中速度的取值范围是[0,350]，加速度的取值范围是[10,10]，而历史运营里程的取值范围为[117 000,350 000]，为避免因其输入参数数值量纲差异过大，导致每个输入参数对输出影响的权重不同，在数据去噪的基础上，还需要对数据进行归一化处理，将输入参数的值域归一化为[0,1]，使各个参数具有同等的权重。

在评价指标上，使用均方差、标准差和算法稳定性来评价转向架部件的服役性能模型。稳定性则是将同一个机器学习算法模型训练M次，得到M个模型，则假设每一次得到的测试集均方差为R1,R2,…,RM，那么稳定性S为：

对所有训练样本进行提取特征、数据去噪、数据归一化和数据划分后，针对动车转向架枕梁垂向振动数据集，文中使用多元线性回归、反向传播神经网络、径向基函数神经网络、回归决策树和随机森林算法建立转向架振动信号监测模型。一共选用了12 859组枕梁振动数据作为训练集，另一组作为验证集，共5 511组数据，训练集和测试集的比例根据经验取为7∶3。分别比较各个模型的训练集、测试集的拟合误差来验证模型的正确性和稳定性，避免求得的模型存在过拟合的问题。

另外通过比较各个模型测试集误差模型的稳定性，验证模型是否存在不稳定的问题。

利用5 511组枕梁垂向振动数据来验证五个模型的有效性。验证集在五个模型上的拟合均方差、标准差和稳定性指标对比如表1所示。

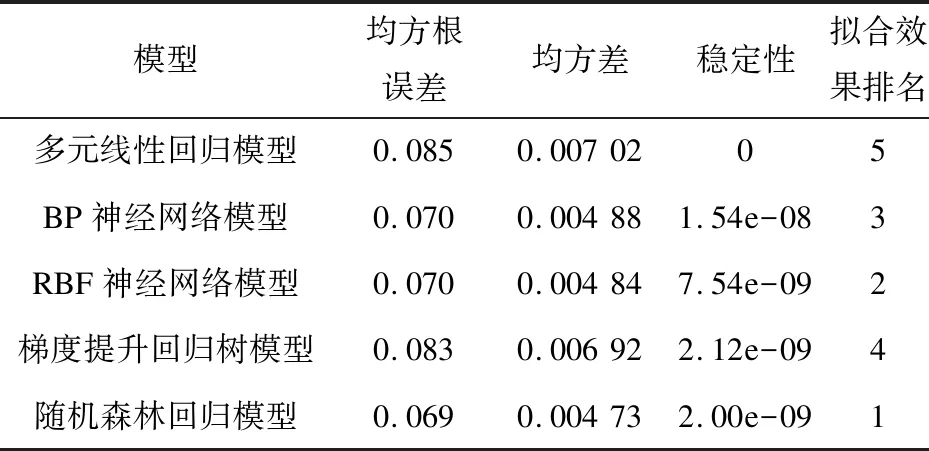
表1 测试集验证结果

从表1中的测试集误差可以直观看出，相对于其他所建立模型的精度，随机森林回归模型比两个神经网络提高了1.4%，比梯度提升树模型提高了16.9%，比多元线性回归模型18.8%。而在模型的稳定性上，随机森林也是优于除多元线性回归之外的其他三个模型，多元线性回归由于每次训练的结果都是一样的，所以其稳定性是最好的，但是其精度确是最差的。

通过对训练集和测试集的实验对比，选取了随机森林模型来预测动车转向架枕梁的垂向振动数据。在11.7万公里的固定里程下，列车的运行速度和运行加速度变化以及所得模型的振动最大值的结果如图4所示。

图4 11.7万公里下的运行速度及枕梁振动最大值预测结果

从列车枕梁的振动数据监测结果看出：当列车处于牵引阶段时，列车的振动最大值是随着运营速度的增加而增加的。当列车处于惰行阶段时，列车会有减速和加速状态，因此振动值是处于震荡变化的；当列车处于减速阶段，随着运营速度的降低，振动值也随之减小。总的来说，模型的预测监测结果与高速列车实际运行情况是十分吻合的。

图5是根据所得模型，预测高速列车在11.7万公里、15万公里、20万公里、25万公里、30万公里、35万公里、40万公里的运营里程下，列车枕梁的振动最大值随列车运行状态的变换关系。

图5 各里程枕梁振动最大值预测结果

从最终选取的模型来看，随机森林模型具备一定的鲁棒性能力，对数据的监测符合其实际的服役性能，能实时预测出在特定里程下，动车转向架枕梁垂向振动值随运行速度和加速度的变化规律。在特定里程下，当列车速度或者加速度超出限速范围，应用该模型可以监测到振动值超出安全阈值。其次，该模型还能监测转向架的振动趋势是否异常。当列车转向架服役里程达到使用年限时，列车转向架的振动值也会超出安全阈值，该模型能制定更加合理的镟修周期，减少列车运营成本。基于机器学习高速列车转向架振动信号的研究对转向架的服役性能分析和安全运行具有重要的指导意义。

实验结果表明，针对动车转向架枕梁垂向振动数据集的监测模型，随机森林回归模型在回归性能上是最佳的。随机森林算法相比于BP神经网络算法、RBF神经网络算法、多元线性回归算法，能更好地保证在转向架部件上复杂的振动信号的数据表现出良好的线性拟合性、数据集适应性以及抗噪性[20-21]。在实现方面，随机森林比其他算法具有更良好的实现性。在处理复杂且多维的实际问题中，随机森林采用特征空间划分学习方式，适应高维数据的处理[22-23]，面对振动信号与动车运营速度、加速度的分析方面具有更好的优化能力。随机森林中各个决策树相互独立，进行学习和预测的效率更高。经过实验验证，在小波变换数据去噪的基础上，基于随机森林算法的实验模型能有效地反映高铁转向架部件服役性能演变规律和安全运行，具有较高的工程应用价值。

4 结束语

列车转向架振动信号是一个振动源复杂，噪音强，数量庞大的数据集，仅靠去噪处理，虽然噪声减少，数据显示效果较好，但是依然具有误差。因此，文中应用具有抗噪性的随机森林算法对数据进行拟合。经过实验表明，基于随机森林的高速列车转向架振动信号监测模型在高速列车安全提速和有效指导合理的维修保养应用中，具有一定的工程价值。为提高监测模型的精准性和有效性，在高速列车转向架振动的安全阈值设置方面需要做进一步的研究。