面向人工智能的浮点乘加器设计
2019-08-22陈正博吴铁彬丁亚军
陈正博,吴铁彬,郑 方,丁亚军
(江南计算技术研究所,江苏 无锡 214000)
0 引 言
随着人工智能应用需求的快速增长,面向人工智能推理和训练的加速芯片已成为该领域重要的发展方向,许多国内外知名的大公司都大力投入相关研发。谷歌TPU、NVIDIA Tesla V100、寒武纪DianNao等是具有代表性的人工智能加速芯片。谷歌公司的TPU[1]以脉动阵列为基础,支持半精度和8位整数的推理应用;寒武纪公司的DianNao系列[2-5]芯片将神经网络各层分解成神经功能单元(NFU),支持半精度的推理应用;英伟达公司于2017年推出了Tesla V100[6]芯片,引入了张量计算单元(tensor core),支持双、单、半精度以及混合精度的训练和推理应用。
浮点乘加部件能力是衡量人工智能芯片性能的主要指标。以NVIDIA Tesla V100为例,该芯片可达到7.5 TFLOPS的双精度计算性能、15 TFLOPS的单精度计算性能和125 TFLOPS的张量计算性能。Tesla V100中包含2 560个FP64的计算单元和5 120个FP32的计算单元,同时引入了640个张量核心。作为人工智能卷积运算的基本单元,张量计算单元的运算方式如图1所示。

图1 Tensor Core基本运算方式
矩阵运算中,A和B都是半精度浮点数(FP16)组成的矩阵,C和D同为半精度浮点数(FP16)或单精度浮点数(FP32)组成的矩阵。当C和D矩阵同为半精度浮点数时,张量计算单元进行半精度的浮点乘加运算;当C和D矩阵同为单精度浮点数时,张量计算单元进行半精度乘半精度加单精度的单半混合精度浮点乘加运算。
考虑到人工智能领域对于各个精度的浮点运算和整数运算都存在需求,研究人员开始进行混合浮点乘加器的相关研究。NVIDIA公司[7]提出了单精度和半精度混合的浮点融合乘加部件。该部件采用双模式实现不同功能,通过硬件复用技术,支持单精度浮点乘加、半精度浮点乘加和半精度浮点乘法后加法的运算模式。
为满足人工智能领域的不同应用场景,人工智能芯片需要集成多种不同精度的运算部件。但目前的人工智能芯片都采用多种独立运算部件集成的技术路线,这些独立的运算部件带来了较大的芯片面积和功耗开销。文中采用跨精度复用的思想,探索通过复用技术进行多种精度混合的浮点乘加部件实现的技术可行性。该研究成果对国产人工智能芯片研发具有重要借鉴意义。
文中设计并实现的面向人工智能的浮点乘加器,支持IEEE-754[8]标准的单精度、并行2个半精度、半精度乘半精度加单精度(单半混合精度)的浮点乘加操作,也支持32位、并行2个16位/8位的整数乘法操作。提出了乘法器复用、移位器复用和前导零预测复用等一系列关键技术,使用复用关键技术设计和实现该浮点乘加器,研究浮点乘加器中各模块的详细设计方法。在完成代码设计后,对其进行功能点和随机数测试,验证浮点乘加器的正确性,同时使用DC工具进行物理综合,结果显示综合运行频率可达2 GHz。
1 面向AI的浮点乘加器的总体结构
文中设计的面向AI的浮点乘加器以经典的浮点融合乘加结构[9]为基础,采用6级全流水结构实现,总体实现结构如图2所示。浮点乘加器的输入数据为32位数据A/B/C和控制信号,在第6级站台输出的数据包括32位浮点乘加结果、浮点异常信号、32位整数乘法结果和乘法溢出信号。该浮点乘加器支持单精度、单半混合精度和并行2个半精度的浮点乘加操作,也支持32位、并行2个16位/8位的整数乘法操作。
文中设计的面向AI的浮点乘加器包括数据预处理、指数差值、对阶移位、乘法器、合并、前导零预测、规格化移位、指数调整、舍入等模块。图2中涂黑的乘法器、移位器、合并、前导零预测模块使用复用技术实现,既解决了跨精度复用功能,又可以优化整体实现的面积和功耗等指标。各模块的功能、跨精度复用技术和详细设计方法将在第2节详细介绍。
在设计的各模块实现后,首先进行功能点和随机数等正确性测试,然后对该设计进行物理综合,根据结果手动调节流水线的划分,使得各级站台之间的时延基本一致,最终的流水线站台划分合理后,再对比单精度和半精度浮点乘加部件比较性能。
2 各模块详细设计方法
本节将介绍各模块的功能、逻辑结构和详细设计方法。该设计中乘法器、移位器、合并与前导零预测等依据跨精度复用思想,使用复用技术实现。
2.1 数据预处理
数据预处理是对输入数据和控制信号提前进行处理,判断计算方式和数据是否符合规范。数据预处理模块的功能分别有指数尾数拆分、输入数据例外异常检测两部分。在数据进入到数据预处理模块时,根据控制信号和部件需要完成的功能,遵守一定的规则,如表1所示。

表1 数据输入规则

图2 面向AI的浮点乘加器总体结构
输入数据满足规则后,还需要对输入异常和例外进行检测,异常情况直接旁路处理,以减少后续计算复杂度。例外和异常结果主要由非数和无穷数产生,除此以外,非规格化数在实际运算过程中会作为0处理。浮点乘加操作的异常产生条件和处理结果如表2所示。

表2 浮点乘加操作异常条件与结果
2.2 指数差值
指数差值模块是根据输入数据A、B和C的指数值,计算对阶移位量和初始结果的阶码。由于不同精度数据的指数值不同,尾数长度也不同,所以分别计算各个精度的对阶移位量和初始结果阶码。在此分别介绍单精度、半精度和单半混合精度的浮点乘加操作中指数差值模块的计算方法。
各种的精度浮点乘加操作,阶差的表达式均为:d=Ce-Ae-Be+bias。
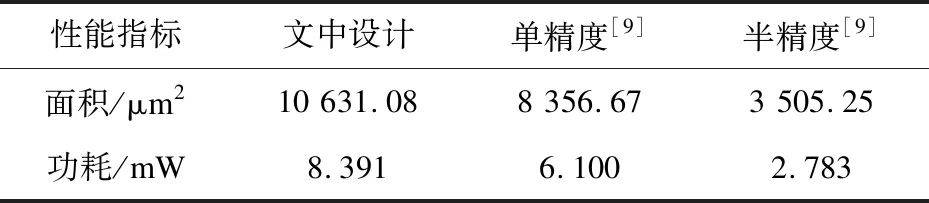
在得到指数域差值d后,可以分别计算对阶移位量和指数阶码。单精度浮点乘加操作的尾数对阶移位示意如图3所示,其中数据位0后表示补0,数据位0前表示尾数在小数点前的部分,小数点前表示尾数在小数点后的部分,可知对阶移位量应为ASC=27-d,结果阶码的初值也应根据阶差大小决定。若d>27,此时ASC为负数,对阶移位量为0,取加数阶码的大小作为乘加结果基础解码;若1 图3 单精度浮点乘加尾数对阶移位示意 文中设计的浮点乘加器分别支持单精度、半精度和单半混合精度的浮点乘加运算,而不同精度的浮点乘加运算中的对阶移位量和乘加结果阶码的计算方式也不相同,需要分别进行分析。单精度、半精度和单半混合精度的浮点乘加运算的ASC、对阶移位量和乘加结果阶码计算方式如表3所示。 表3 对阶移位量和结果阶码的计算方式 在该设计中,移位器包括对阶移位器和规格化移位器两种。对阶移位器的功能是进行尾数C和乘法结果的对阶,规格化移位器的功能是进行中间尾数结果与规格化数的对阶。虽然各模块的功能不同,但移位器的跨精度复用思想一致。 移位器跨精度复用设计方法介绍如下:以对阶移位为例,单精度浮点乘加需求76位移位器,半精度浮点乘加需求37位移位器,混合精度浮点乘加需求50位移位器,考虑到该设计支持一个单精度乘加、并行两个半精度乘加、一个混合精度乘加的操作,使用一个37位和一个76位的桶形移位器[10]可满足需求,在移位器前后分别加上移位位数选择器和结果选择器,完成对阶移位器模块的复用设计。 以规格化移位为例,单精度浮点乘加需求52位移位器,半精度浮点乘加需求26位移位器,混合精度浮点乘加可直接复用单精度操作完成。同样地,使用一个26位和一个52位的移位器,并在前后分别加上移位位数选择器和结果选择器,即可完成规格化移位器模块的复用设计。 乘法器是该设计中最重要的单元,包括部分积生成和部分积压缩两个部分,计算方法是按位拆分,分别计算再进行合并。乘法计算公式为: 将公式中括号内的内容进行Booth-4编码[11-12],生成以A为基础的16个部分积,再通过部分积压缩树将部分积压缩成Carry和Sum结果。跨精度复用技术在部分积生成和部分积压缩树两部分中都有体现。进行并行两个的半精度数计算的操作中,在生成后8个部分积时,A和B低位填充第一个半精度数,高位填零;生成前8个部分积时,A和B低位填零,高位填充第二个半精度数。这样的填充方法可直接进行压缩,不影响最终结果,得到的后8个部分积压缩后得到第一个半精度数乘法结果,前8个部分积压缩后得到第二个半精度数乘法结果。部分积生成完成后进行部分积压缩,复用的部分积压缩树的结构如图4所示。 产生的16个部分积首先经过两层4∶2的CSA压缩树,此时产生的4个分量结果与2个半精度特殊分量分别进行3∶2CSA压缩后即可输出2个半精度结果;若其中两个分量结果直接与单精度特殊分量进行压缩可输出单半混合精度结果;而4个分量经过4∶2CSA压缩树后再与单精度特殊分量进行压缩可得到单精度结果,所以此时需要增加一个MUX选择器,根据控制信号中的精度信息进行分量选择,这样最终可得到半精度、单精度或是单半精度的浮点数乘法中间结果Carry和Sum。值得注意的是,整数乘法也可借用此逻辑复用实现,8位整数乘法套用半精度整数乘法,16位整数乘法套用半精度整数乘法,32位整数乘法套用单精度整数乘法即可。 图4 部分积压缩树 得到Carry和Sum后,需要将这两个分量合并成一个分量,同时并行使用这两个分量进行前导零预测,预测合并后的分量前方有多少个零,这样在分量合并得到结果后,同时通过前导零预测模块得到的规格化移位位数,直接进行规格化移位,从而减少关键路径时延。 合并模块的功能是将Sum和Carry分量合并到一起,得到尾数计算的中间结果,通常使用加法器即可实现。合并模块的跨精度复用实现技术比较直观,由于单精度、半精度和单半混合精度的输入数据大小不同,按照最低位数拆分并处理,并行使用4个41位的超前进位加法器[13],输入进位分别设置为0和1,4个加法器根据控制信号分别输入各种精度的浮点或整数乘加的Sum和Carry(位数不足时分别补0和1),然后将加法器结果通过选择器可得到不同精度的合并数值。 前导零预测模块的功能是根据Sum和Carry分量预测计算两个分量合并后的首1位置。前导零预测模块的核心算法是LZA算法[14],即对两个操作数做减法计算,得到数零位串,对得到的数零位串通过树形结构LZD预测第一个1的位置,即可得到前导零预测的结果。 前导零预测的跨精度复用思想和设计技术与合并模块类似,单精度和半精度的数零位串的长度分别为52位和26位,考虑到LZD预测树的高度可扩展性,使用长度为2的次方数的LZD树形结构。按照最低位数拆分并处理,并行使用两个32位的LZD预测树,根据两个预测树分别输出的有效位和预测数值进行逻辑判断,通过选择器后,最终得到不同精度需求的规格化移位位数。由于前导零预测算法本身可能会存在1位的误差,且加法和减法可能存在1位误差,所以至多存在2位的误差,需要在规格化移位结束后进行检测,若存在误差则进行指数和尾数的修正。值得注意的是,在乘法器输出结果之后,单半混合精度与单精度结果的处理方式完全相同,不会额外增加逻辑。 指数调整模块的功能是消除误差,得到准确的指数值。由于前导零预测本身可能存在至多2位的误差,故在规格化移位后进行简单的逻辑判断,计算出指数调整和尾数移位的数值,使用加法器即可得到最终结果的指数值,并对尾数再进行一定量的移位得到最终结果的尾数值。 舍入模块的功能是对最终结果进行舍入,并合并指数尾数结果得到最终的输出结果和异常或溢出信号。得到最终结果的指数值和尾数值后,结合舍入位和粘贴位的数据,舍入模块根据控制信号提供的4种不同的舍入方式进行舍入,得到正常的计算结果,同时与异常处理结果合并,即可最终输出浮点乘加结果、浮点异常信号、整数乘法结果和整数溢出信号,完成面向AI的浮点乘法器功能。 完成代码设计后,撰写激励使用PSL语言对浮点乘加器进行正确性测试,验证面向人工智能的浮点乘加器是否满足正确性要求。正确性测试主要分为功能点测试和随机数测试两个方面。第一是功能点测试,对于各种异常的输入分别制造激励进行测试,直到所有的异常情况都被覆盖,从而检测浮点乘加器的异常处理机制是否完备;第二是随机数测试,对于表1中列举的各种部件功能,包括单精度、半精度和混合精度三种精度浮点乘加,和32/16/8位定点乘法,分别生成十万组不同的随机数数据,测试各个功能的结果是否保持正确,从而检测浮点乘加器的各功能都能正确使用。功能点和随机数测试的结果显示,文中设计的面向AI的浮点乘加器结果满足正确性要求。 使用Synopsys公司的Design Compiler工具,基于28 nm工艺库条件对浮点乘加器进行物理综合。物理综合结果显示,该部件的综合运行频率可达2 GHz。 为了评估该部件的功耗和面积等指标,体现该设计的优越性,在相同条件下,分别对单精度浮点乘加部件[9]、半精度浮点乘加部件[9]和设计的面向AI的浮点乘加器进行物理综合,并对面积和功耗等性能指标进行对比,结果如表4所示。 表4 性能对比 对比的结果可以发现,文中设计的面积比经典的单精度浮点乘加部件增加了27.2%,功耗增加了37.55%。考虑完全无复用的设计,完成面向AI的浮点乘加器的计算功能需求至少需要1个单精度部件和2个半精度部件,同时需要1个单半精度混合部件,且单半精度混合部件的面积和功耗比半精度部件要大,在计算无复用结果时可进行累加。最终结果显示,该设计比完全无复用设计的面积至少减少50.09%,功耗至少减少47.91%。 总而言之,该设计使用跨精度复用技术[15],在保证频率可接受范围内,大幅度减少了设计的硬件实现消耗,优化了浮点乘加器的性能,提出的复用技术具有显著意义。 文中研究和设计了一种面向AI的浮点乘加器,支持32位、并行2个16位/8位的整数乘法运算,同时支持单精度、单半混合精度、并行2个半精度的浮点乘加运算。采用跨精度复用思路,详细讲解了各模块的功能、详细设计方法和跨精度复用实现方案。跨精度复用技术是文中的主要创新点,提出了乘法器复用、移位器复用和前导零预测复用等一系列关键技术。完成代码设计后,对浮点乘加器进行了正确性测试,结果表明浮点乘加器能够满足正确性要求。使用DC工具对浮点乘加器进行硬件综合,结果显示该设计类比于无复用设计,减少了至少50.09%的面积、47.91%的功耗,综合运行频率可达2 GHz。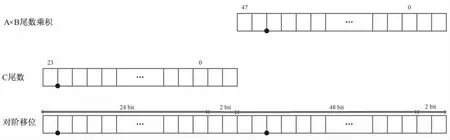

2.3 移位器
2.4 乘法器

2.5 合并与前导零预测
2.6 指数调整与舍入
3 实验分析
3.1 正确性测试
3.2 物理综合
4 结束语
