一类具有Allee效应的捕食-食饵模型正解的唯一性和渐近行为

李海侠

(宝鸡文理学院数学与信息科学学院，陕西宝鸡721013)

本文讨论如下捕食-食饵扩散模型:

其中Ω是RN中带有光滑边界∂Ω的有界区域，u和v分别表示食饵和捕食者的浓度，a和d分别是u和v的最大增长率。是加法Allee效应项，m和n是Allee效应常量，反映了Allee效应的强弱程度；若m＞br，则表现为强Allee效应，若m＜br，则表现为弱Allee效应。是Crowley-Martin(C-M)反应函数，是一类依赖捕食者的经典反应函数之一。它与Beddington-DeAngelis(B-D)反应函数很像，不同之处在于分母多了体现物种间相互干扰的一项bcuv。而且，C-M反应函数认为无论某个捕食者目前是否寻找或处理食饵，都允许存在捕食者间的干扰，这是比B-D反应函数优越之处，也非常符合现实中的一些生物现象。因此研究带有C-M反应函数的模型具有很大的生物意义。系统(1)中的参数a，m，n，b，c，d，p，q，k都是正常数。u0(x)，v0(x)是连续函数。

近年来，随着全球环境的不断变化，很多种群会受到Allee效应的影响。Allee效应会影响种群系统的稳定性，甚至导致某些种群灭亡。因此，具有Allee效应的模型受到了生物学家和数学家的广泛关注[1-8]，其中文献[4-6]在齐次Neumann边界条件下讨论了具有加法Allee效应的捕食-食饵模型，文献[7]讨论了具有加法Allee效应和B-D反应函数的捕食-食饵模型，利用稳定性理论得到了正解的唯一性和稳定性。然而由于加法Allee效应项的引入使得系统的研究变得复杂，所以目前在齐次Dirichlet边界条件下对带有加法Allee效应和C-M反应函数的捕食-食饵扩散模型的研究很少见。

鉴于此本文主要讨论系统(1)的渐近行为以及系统(1)对应平衡态系统

正解的唯一性和稳定性。

1 正解的存在性

本节利用不动点理论给出系统(2)正解存在的条件。先给出一些预备知识。

令λ1(q)是-Δ+q(x)在Ω上关于齐次Dirichlet边界条件下的主特征值，则λ1(q)是单重的。而且，如果q1(x)≤q2(x)且q1(x)≢q2(x)，则λ1(q1)＜λ1(q2)。简单起见记λ1(0)=λ1。

众所周知如下问题

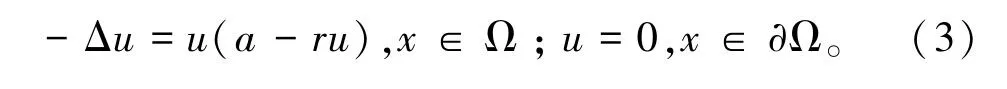
当a＞λ1时，式(3)存在唯一正解，记为(a，r)。而且(a，r)＜。特别地，记(a，1)为a。

考虑单物种问题

易知当m＜n2，a＞λ1+时，式(4)存在唯一正解，记为。而且＜a＜a。同理，当d＞λ1时，系统(1)存在半平凡解(0，)。简单起见记为。因此，在一定条件下系统(2)存在两个半平凡解(，0)和(0，)。

首先由特征值的比较原理给出系统(2)正解存在的必要条件。由于证明是基本的，所以在此省略。

引理1如果(u，v)是系统(2)的正解，则a＞λ1，d＞ λ1。

接着利用上下解方法有如下正解的先验估计。

引理2系统(2)的任意正解(u，v)满足u≤a＜a，v～≤v≤d＜d。

证明由系统(2)的第一个方程得

-Δu≤u(a-u)，x∈Ω；，u=0，x∈∂Ω，于是根据a的唯一性和上下解方法有u≤a＜a。同理可得v～≤v≤d＜d。

为了利用度理论我们引入如下空间

定义算子Aτ:E→E为

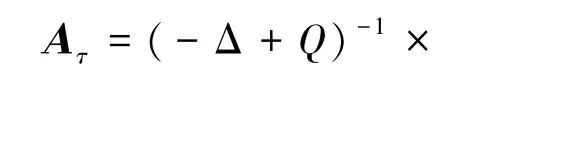
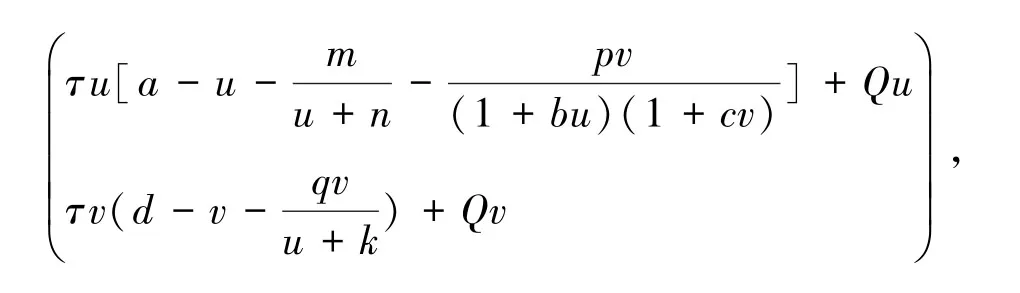
其中τ∈[0，1]，q是充分大的正常数。显然Aτ是紧算子。记A=A1，则易知A:D→W是连续可微算子。

系统(2)在平凡解和半平凡解处的指数计算证明与文献[7]中的引理3类似，所以在此省略。

引理3(i)设a≠λ1+，d≠λ。若a＞λ+11或d＞λ1，则indexW(A，(0，0))=0；若a＜λ1且d＜λ1，则indexW(A，(0，0))=1。

(ii)indexW(A，D)=1。

(iii)设m＜n2，a＞λ1+。 若d＞ λ1，则indexW(A，(u～，0))=0； 若d＜ λ1，则indexW(A，(，0))=1。

(iv)设d＞λ1。若a＞λ1，则indexW(A，(0，v～))=0； 若a＜ λ1则indexW(A，(0，v～))=1。

于是

定理1如果

m＜n2，a＞ λ1，d＞ λ1，

则系统(2)至少存在一个正解。

证明由已知条件和引理3有

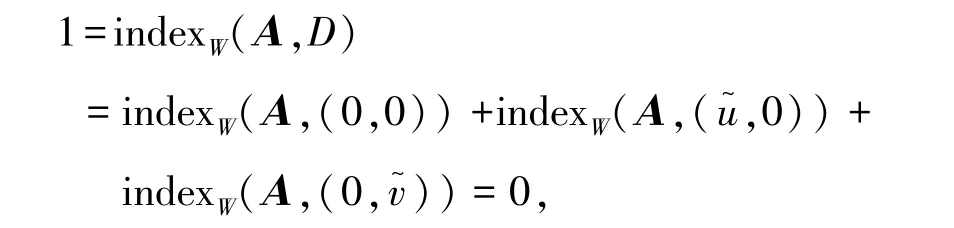
因此根据不动点指数的可加性知结论成立。

2 正解的唯一性和稳定性

我们研究当c充分大时，系统(2)正解的唯一性和稳定性。考虑如下问题

引理4设m＜n2，a＞λ1+，d＞ λ1。 则系统(5)存在非退化且线性稳定的唯一正解(，)。这里是如下问题的唯一正解

证明根据文献[9]定理2.1(iii)可知正解的存在性和唯一性显然。令L(，)是系统(5)在(，)处的线性化算子，则

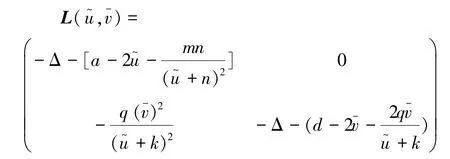
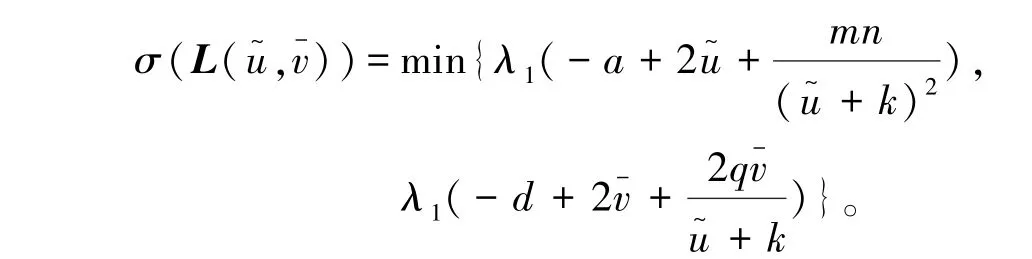
若m＜n2，则

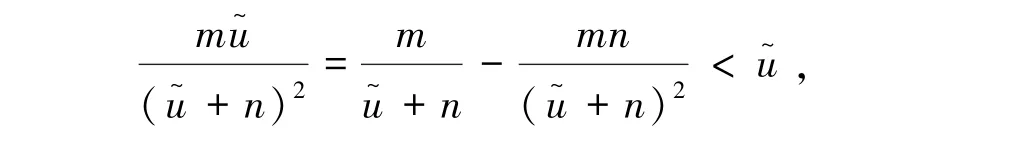
因此，σ(L(u～，v-))＞0。 故结论成立。

最后给出系统(2)正解的唯一性和稳定性结果。

定理2设m＜n2，a＞λ1()+，d＞ λ1。则当c充分大时，系统(2)存在唯一正解且线性稳定。

证明首先由定理1可知系统(2)存在正解。显然当c充分大时，系统(2)是系统(5)的正则扰动。于是根据引理4和扰动理论可知系统(2)的任意正解非退化且线性稳定。又根据紧性理论和假设可知系统(2)至多有有限个正解。记为{(ui，vi):0≤i≤n}。 通过以上讨论可知，I-A′(ui，vi)在(ui，vi)上可逆，且A′(ui，vi)没有大于1的实特征根。又因为(ui，vi)=S(ui，vi)，所以A′(ui，vi)在(ui，vi)上没有α性质。故根据文献[10]的定理1有indexW(A，(ui，vi))=1。最后根据引理3和度的可加性得

1=indexW(A，D)=(A，(ui，vi))+0=n，因此系统(2)存在唯一正解。

3 渐近行为

利用抛物方程的比较原理讨论系统(1)的灭绝性和持久性。首先讨论平凡解和半平凡解的稳定性以及系统的灭绝条件。

定理3(i)若a≤λ1且d≤λ1，则当t→∞时，(u，v)→(0，0)。而且，若a＞λ1+或d＞ λ1，则(0，0)不稳定；若a＜λ1+且d＜λ1，则(0，0)稳定。

(ii)设m＜n2，a＞λ1+。 若d≤λ1，则当t→ ∞时，(u，v)→(，0)。 而且，若d＞ λ1，则(，0)不稳定；若d＜ λ1，则(，0)稳定。

(iii)设d＞ λ1。 若a≤λ1，则当t→∞时，(u，v)→(0，v～)。 而且，若a＞ λ1()+，则(0，)不稳定；若a＜λ1()+，则(0，)稳定。

证明由于证明类似，故在此只证明(ii)。因为m＜n2，a＞ λ1+且

则由前提d≤λ1和比较原理得当t→∞时，v(x，t)→0。 于是存在T′ε≥0使得当t＞Tε′时，v(x，t)＜ε。则

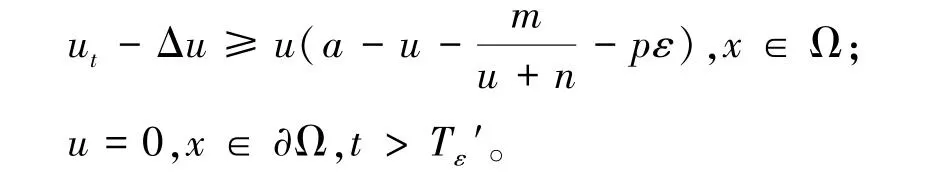
于是利用ε的连续性和比较原理可知当t→∞时，u(x，t)→。

最后证明稳定性结果。考虑如下特征值问题

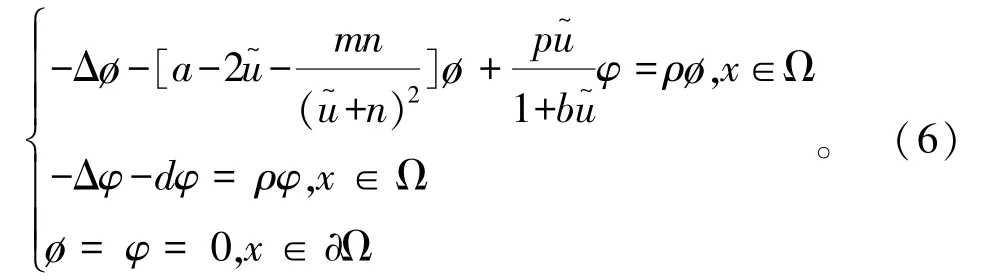
易知特征值问题(6)的特征值ρ1=min{λ1(-a+2+)，λ1(-d)}。同引理4的证明可知λ1(-a+2+)＞0。当d＞λ1时，λ1(-d)=λ1-d＜0，所以(u～，0)不稳定。 当d＜λ1时，λ1(-d)=λ1-d＞0，所以(，0)稳定。

这节最后给出系统(1)持久性条件。

定理4若m＜n2，a＞λ1++，d＞ λ1，则存在(，)和(，)使得

和方程组

证明首先易知f(u，v)=(u[a-u--]，v(d-v-))混拟单调。由上下解定义可知(，)和()是系统(1)的一对上下解。 而且，(f(u，v)，g(u，v))在[]×[，]上满足Lipschitz条件。于是根据单调迭代方法得满足式(7)和(8)的函数对(，和(，)存在。

且vt-Δv≤v[d-v-]。于是sup v(x，t)≤。 因此存在Tε′≥0使得当t＞Tε′时，

另外，由系统(1)可知

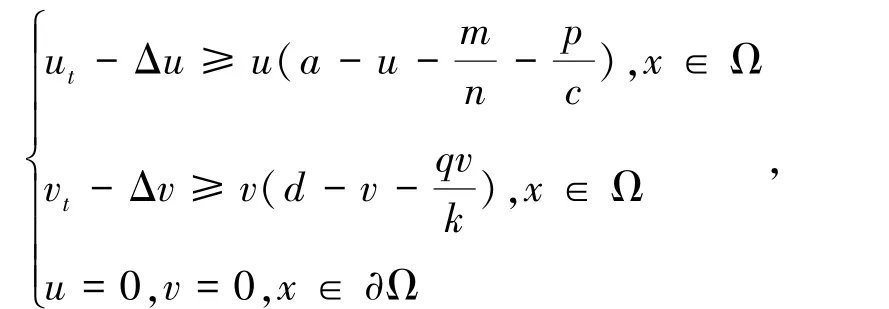
再次由比较原理可知

于是存在Tε″≥0使得当t＞Tε″时，

最后，令T*={Tε，Tε′，Tε″}。 对于所有的t＞T*和ε ＞0，由式(9)-(11)得

令ε→0，根据文献[11]中的性质2.1和定理2.1知结论成立。