夹具拘束下大型薄壁铝合金结构搅拌摩擦焊接变形特性
2019-08-21汤一博孙宏波余海东来新民
汤一博 孙宏波 余海东 郑 斌 来新民
1.上海交通大学上海市复杂薄板结构数字化制造重点实验室,上海,2002402.首都航天机械有限公司,北京,100076
0 引言
铝合金大型薄壁结构质量小、耐腐蚀、加工性能优异、易于连接,广泛应用于航空航天等领域,如大型飞机、火箭的贮箱结构等[1]。这类产品多为大尺寸薄壁结构,其尺寸精度直接影响整机性能。随着尺寸的增大,薄壁结构的刚度降低,同时受几何非线性影响,焊接变形更大。焊接过程中主要靠夹具约束提高焊缝附近的局部刚度,以控制焊接变形,然而不同的夹具拘束位置对大型薄壁结构焊缝处刚度的影响程度不同,进而导致焊接变形不同,对大型薄壁结构的焊接变形影响更加明显。
近年来,国内外很多学者针对焊缝长度较小的结构通过试验和数值模拟方法来研究外部拘束对焊接变形和应力的影响。张建强等[2]采用热弹塑性方法对4种不同夹具拘束情况下500 mm长的铝合金薄板焊接过程进行了仿真,结果表明,采用合理的夹具布局可以将薄板的纵向挠度控制在1 mm左右。WAHAB等[3]的焊接实验表明焊接件所受外拘束力是动态变化的,可采用位移约束来保证焊接件不变形。张增磊等[4]将夹具和垫板作为弹塑性体应用到焊接数值模型中,采用4种模型模拟夹具、垫板与焊接件之间的相互作用,结果表明夹具拘束作用的不同处理方式对平板焊后残余应力分布与变形有重要影响。刘川等[5-6]采用表面堆焊方式对尺寸为200 mm×150 mm×6 mm的焊接件建立多体耦合模型,研究了外拘束大小、作用位置对焊接变形和残余应力的影响,发现若拘束弯矩相同,则焊接变形基本一致。郭玉全等[7-8]采用三维热力耦合模型探究了夹具拘束距离对尺寸为100 mm×25 mm×0.5 mm的Hastelloy C-276薄板脉冲激光焊接变形的影响。区达铨等[9]针对复杂框架结构,采用分段移动温控体热源高效算法,研究焊接顺序对焊接应力和变形的影响。SCHENK等[10]建立了包含夹具在内的有限元模型,分析了夹具对薄板焊接变形的影响,研究了夹紧时间、夹具释放时间和夹具预热对焊接失稳变形、弯曲变形和角变形的影响。上述研究表明夹具拘束对薄板结构焊接变形有重要影响,随着结构尺寸的增大,薄板的结构刚度降低,夹具拘束作用将更加显著,而目前关于长程焊缝的大型薄壁结构的研究较少。
对于预测焊接变形的计算方法,目前多采用精度高、结构适应性强的移动热源方法,但是该方法单元依赖性强,计算耗时长[11],难以应用于大型结构。固有应变法[12]是解决大型结构焊接变形问题的一种有效方法,该方法规避了复杂的焊接过程,提高了计算效率,但它施加在焊缝区域的应变为均匀分布, 忽视了大型薄壁结构的刚度下降和几何非线性对翘曲变形的影响,虽然提高了焊接计算效率,但是随着尺寸的增大和结构刚度的变弱,难以准确预测大型薄壁结构的焊后变形。因此还需要进一步探究能够准确预测大型薄壁结构焊接变形的方法。
本文采用一种新的方法——应力分区映射法计算大型薄壁结构的焊接变形,通过对局部小模型进行热力学分析得到夹具释放前的焊接应力分量,将应力分量映射到全局大模型对应的焊缝区域,进行一次弹性变形计算从而得到大型薄壁结构的焊接变形,用实验结果验证该方法的正确性,并从机理上分析搅拌摩擦焊的变形行为,在此基础上研究了不同焊缝长度的薄壁结构在不同夹具拘束距离下的焊接变形规律。
1 应力分区映射法
应力分区映射法的原理如图1所示。将局部小模型和整体大模型分别划分为焊接起始区域、稳态区域和结束区域,整体大模型中弹性区等效为子结构,以边界条件的形式施加在局部小模型的边界。考虑材料和几何非线性影响对小模型进行热力学分析得到6个焊接应力分量,通过插值计算方法将小模型三个区域的应力分量分别映射到大模型的焊缝区域,最后大模型只需要进行一次弹性变形计算即可得到结构的焊接变形。

图1 应力分区映射法的原理图Fig.1 Schematic of stress mapping method
1.1 弹性区子结构
焊接过程中产生的应力和应变主要出现在焊缝及热影响区的局部区域,而非焊接区结构在整个过程中可以看成是弹性的。弹性区虽然并未经历剧烈的温度变化,但它对焊缝及其附近热影响区的应力应变过程存在约束作用,通过将其作为子结构,引入非焊接区域的弹性影响,可以大大提高计算效率。
将普通有限元单元用矩阵凝聚为一个超单元即为子结构。为了减少非焊接区域总自由度数,需要对节点进行合理编号,将节点位移分解为两部分
(1)
式中,dA为要保留的节点位移,称“边界节点”;dB为需要去除的节点位移,称“内部节点”。
同时将刚度矩阵也写成分块矩阵的形式,则平衡方程为
(2)
式中,KAA为边界单元组成的刚度矩阵;KBB为内部单元组成的刚度矩阵;KAB、KBA为其余单元组成的刚度矩阵;FA和FB为载荷向量。
将式(2)化简得
(3)
凝聚后子结构超级单元的刚度和载荷向量分别为
(4)
在完成内部自由度凝聚即获得子结构刚度矩阵和载荷矩阵之后,将其引入局部小模型的焊接计算中,以此来反映大型薄板非焊接区域的约束作用。
1.2 应力分量映射
应力分量映射过程是将小模型经过热力分析得到的6个应力分量映射到大模型的长焊缝中。实际工程结构一般含有多条焊缝,为了节省计算时间,通常同样类型的焊缝只进行一次小模型分析,因此需要将大模型的坐标转换到小模型的坐标系下。设局部小模型坐标系的原点为O,整体大模型坐标系的原点为O′,假设O在整体模型坐标系下的坐标d=(x0,y0,z0),则局部模型坐标系相对于整体模型坐标系的旋转矩阵可表示为
gRl=[gxlgylgzl]
(5)
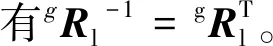
整体大模型坐标系下的积分点坐标gP可以转换到局部模型坐标系下的坐标lP,如下式所示:
(6)
为了计算准确,数值模拟采用的网格类型为三维二次缩减单元类型C3D20RT,每个单元有8个积分点。单元积分点的应力是在仿真过程中获得的准确值,根据式(6)的坐标转换公式,将整体模型各单元的积分点坐标转换到局部小模型坐标系下,搜索每个坐标转换后单元积分点所属局部单元的最近积分点。将整体大模型各单元的积分点坐标映射到等参单元,为后续应力分量插值计算提供条件。8积分点等参单元的插值函数可以表示为
(7)
ξ0=ξξ1η0=ηη1ζ0=ζζ1
其中,ξ1、η1和ζ1分别为等参单元各节点三个方向的坐标,ξ、η和ζ为整体大模型积分点坐标映射到等参单元后的坐标,可由下式的插值方程求得:
lP=S0lQ
(8)
其中,lP为整体大模型积分点经过坐标转换后的坐标矩阵,lQ为局部小模型中相应单元的8个积分点坐标,矩阵S0可以表示为
(9)
通过插值得到对应的等参单元内的坐标ξ、η和ζ的值后,整体大模型积分点的应力分量由下式计算得到:
(lσg)vec=S(lσl)vec
(10)
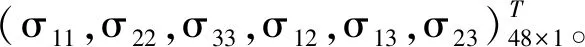
矩阵S的形式如下:
S=
(11)
为了预测结构的最终变形,需要将在局部坐标系下计算得到的应力分量转换到整体大模型坐标系下,在转换过程中首先将应力写成张量形式:
(12)
由坐标转换矩阵,将式(12)的应力张量转换到整体大模型坐标系下,转换表达式如下:
(13)
其中,gRl为旋转矩阵;gσg为整体大模型各积分点在全局坐标系下的应力张量。将应力张量作为初始应力施加到整体大模型的焊缝区域,进行一次弹性过程计算即可获得焊后变形。
1.3 焊接模拟模型
根据1.2节应力分区映射法的原理,采用有限元软件ABAQUS进行仿真计算。分析时采用的局部小模型和整体大模型如图2所示,局部小模型尺寸为140 mm×280 mm×6.8 mm,整体大模型尺寸为300 mm×1 000 mm×6.8 mm,小模型尺寸为80 mm×1 000 mm×6.8 mm,将两侧子结构刚度凝聚后保留与小模型接触节点的自由度并与小模型连在一起,作为弹性约束。2个模型均采用20个节点、可进行热力学计算的二次缩减积分网格类型C3D20RT,焊缝两侧的40 mm区域采用大小为5 mm的六面体网格均匀划分,远离焊缝区域采用大小为10 mm的六面体网格均匀划分。由于焊接过程中薄板沿厚度方向变形明显,因此为保证计算结果精度,厚度方向划分成3层网格。小模型的单元总数为2 697,大模型的单元总数为22 800。
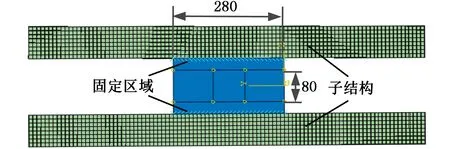
(a)小模型

(b)大模型图2 有限元模型Fig.2 FE models
同时考虑热传导和热辐射问题,焊接过程中焊接件底面与工作台之间的热传导比焊接件与环境之间的热传导大。焊接时对小模型两侧距焊缝40 mm处30 mm宽的夹具位置约束节点3个方向自由度,试样底面也固定3个方向自由度,以模拟工作台的支撑作用。焊后释放所有的边界约束,让平板自由变形,同时固定大模型中焊缝起始位置的一个点,防止发生刚体位移,如图2b所示。
1.4 材料性能参数和热源模型
2024-T3铝合金在不同温度下的质量热容、热膨胀系数、热导率、弹性模量和屈服强度如表1所示[13]。
在搅拌摩擦焊接过程中,搅拌轴肩、搅拌头和焊接件之间存在复杂的摩擦作用。焊接过程中总的热量输入Qin与主轴转速ω和扭矩M相关,主轴的机械功P基本上全部转化为了热量。总热量输入Qin可以划分为轴肩处的面热源QS和搅
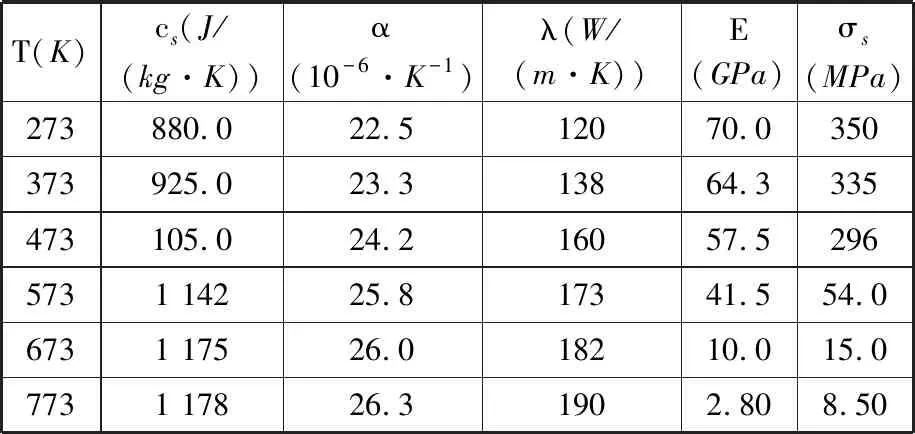
表1 材料的热力学参数随温度的变化Tab.1 The thermal and mechanical parameters of the material changed with temperature
拌针区域的体热源Qp两部分:
Qin=ηP=ηMω=QS+Qp
(14)
其中,η为机械功转化为热量的比例系数,这里采用η=0.95[14]。
轴肩作用区域可以等效为一个平面圆环,圆环的外径为r0,内径为搅拌针直径rp。搅拌头轴肩和试样接触面间的热量QS可以表示为
(15)
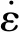
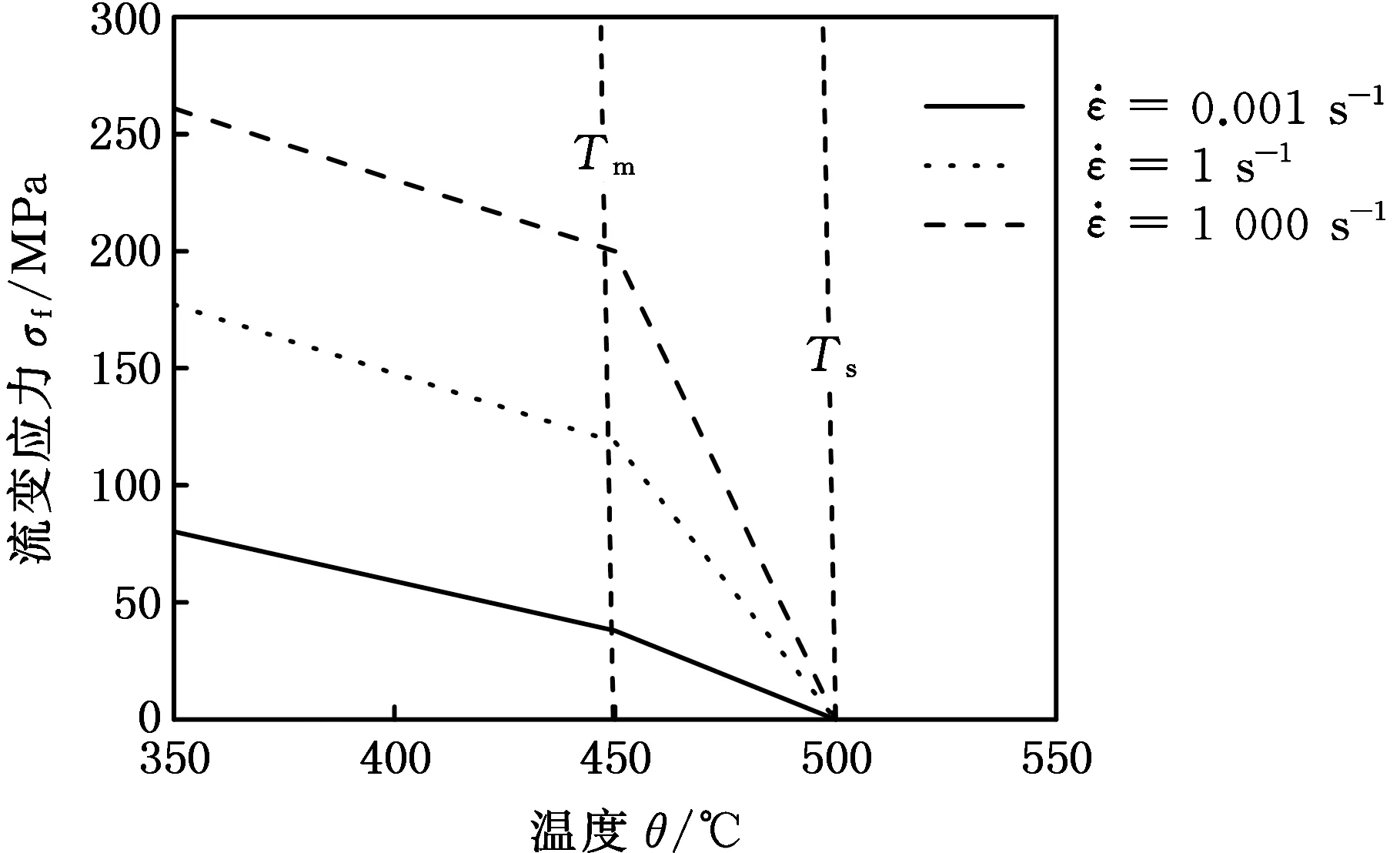
图3 铝合金2024-T3流变应力变化曲线Fig.3 Flow stress curves of aluminum alloy 2024-T3
搅拌针的热输入Qp由搅拌针表面和材料摩擦产生,因此搅拌针区域的体热源可以写为
(16)
式中,hp为搅拌针的高度。
相应地,搅拌头轴肩的热流密度qS和搅拌针的热流密度qp分别为
(17)
在搅拌摩擦焊过程中,同时考虑热作用和搅拌头对焊接件的压力作用。将搅拌头的下压力以均匀分布的载荷施加在薄板上表面的搅拌头作用区域内,可以写为
(18)
式中,Fz为下压力;p为压强。
将上述热源模型采用ABAQUS的Dflux子程序,均布载荷采用Dload子程序,施加到小模型的焊缝上。
2 搅拌摩擦焊实验
搅拌摩擦焊实验的焊接件尺寸及材料与仿真模拟的尺寸与材料一致,为两块150 mm×1 000 mm×6.8 mm的薄板,材料是2024-T3铝合金。夹具宽度为30 mm,夹具拘束距离选择40 mm。焊接试件和焊接设备如图4所示,该设备工作台尺寸为2 000 mm×3 000 mm,通过下压量和下压力两种控制方法均可实现搅拌头下压,下压力最大可达40 kN,主轴电机最大输出功率为50 kW,搅拌头转速最高可达3 000 r/min,进给速度最高可达2 500 mm/min。本实验采用的搅拌摩擦焊工艺参数如表2所示。焊接过程中搅拌头的轴向力为2 019 N,搅拌头轴肩半径和搅拌针半径分别为10 mm和3 mm,因此轴肩与工件表面的压力为7.1 MPa。

图4 试样件和焊接设备Fig.4 Test specimen and the welding equipment

表2 搅拌摩擦焊的工艺参数Tab.2 Process parameters in FSW
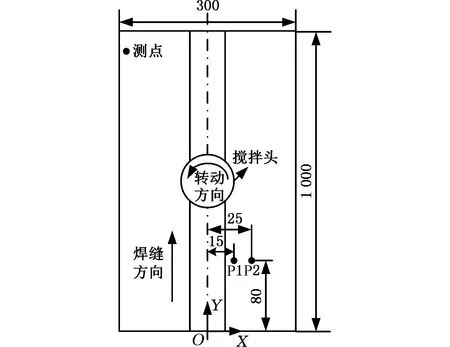
图5 温度测量点的布置Fig.5 Locations of measurement points
采用IR公司生产的A615型固定安装式红外热像仪对焊接过程中的温度进行测量,其测量精度为± 2 ℃。由于焊接实验自身过程的限制,温度测量位置只能取在轴肩外侧一定范围内,测量点的布置如图5所示,两个测点P1、P2在焊缝方向上距起始位置为80 mm,与焊缝中心的垂直距离分别为15 mm和25 mm。
焊接变形存在明显的面外变形,同时考虑到焊接试样的尺寸较大,采用激光跟踪仪测量焊后结构型面,其测量精度为0.005 mm/m。焊接试样及测量设备如图6所示。

图6 焊接试样及测量设备Fig.6 Measurement of welding distortion and welded workpiece
3 计算结果与分析
3.1 仿真与实验结果对比
针对尺寸为1 000 mm×150 mm×6.8 mm两块平板的搅拌摩擦焊过程,采用应力分区映射法,在距焊缝40 mm的夹具拘束距离下进行仿真计算。经过热力学分析得到小模型焊接过程中试样表面温度分布,如图7所示,搅拌摩擦焊接圆形搅拌头轴肩形状与图中最高温度分布的圆形区域一致。
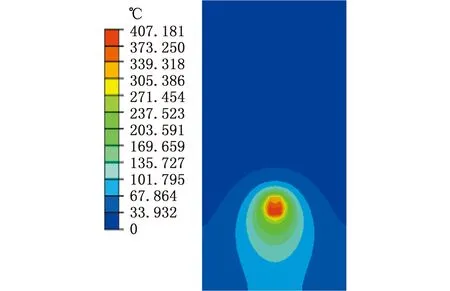
图7 焊接模拟过程试样的温度分布(t=16 s)Fig.7 Temperature distribution in the welding simulation process(t=16 s)
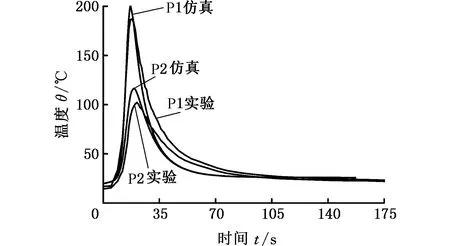
图8 两个测量点仿真和实验的焊接温度对比Fig.8 Welding temperature comparison of numerical results and experimental data for two test points
图8对比分析了仿真模拟温度和实验测量温度随时间的变化规律。从图8可知,仿真结果和实验数据一致性良好,仿真结果的温度峰值略高于实验结果的温度峰值,原因在于实验环境的初始温度为4 ℃,而仿真计算中初始温度为20 ℃,初始温度的差异导致了仿真结果略高于实验结果。
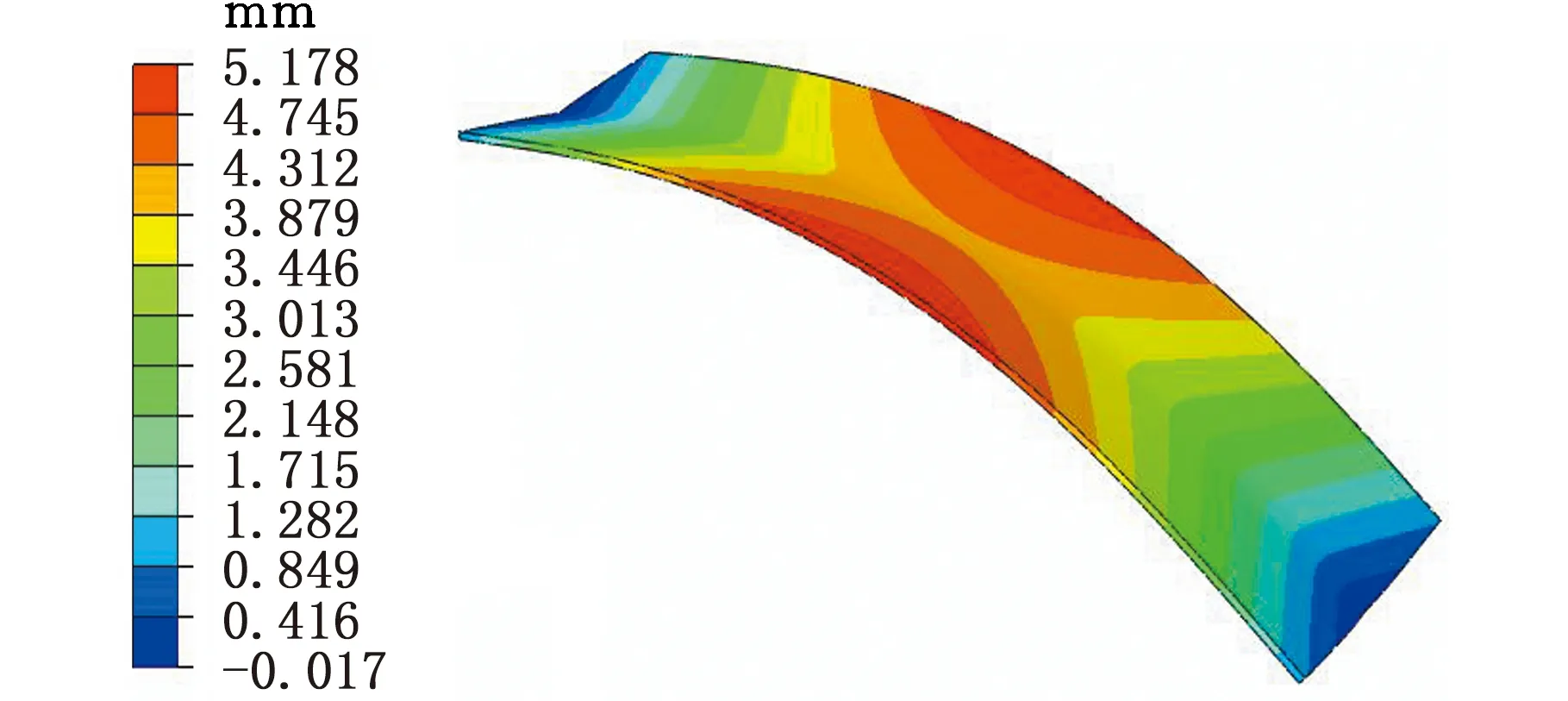
(a)仿真结果

(b)实验结果图9 焊接变形仿真与实验结果对比Fig.9 Welding deformation comparison of simulation and experimental results
图9所示为焊接变形的仿真结果与实验结果对比,图9a所示为焊接变形仿真结果,图9b所示为由实验测量的点云数据绘制的焊接变形量。由数值仿真和实验结果对比可以发现,两者焊接变形趋势相同,均出现反马鞍的变形,沿焊缝纵向方向呈现上凸弯曲变形,沿板宽度方向呈现下凹的角变形。并且仿真和实验在z方向的变形跨度均为0~5.2 mm。最小变形出现在焊缝的起始端和结束端,最大变形发生在焊缝中间截面板边缘位置。
图10所示为焊接板边缘沿焊缝方向仿真和实验焊接变形的对比曲线。由图10可知,仿真的变形最大值略高于实验的变形结果。焊接板边缘仿真最大变形为5.178 mm,实验测量最大变形Dmax为5.2 mm,实验与仿真的最大差值emax为0.41 mm,计算得到焊接变形的相对误差emax/Dmax为7.8%,精度可达92.2%。从计算效率角度看,采用应力分区映射法计算1 m平板的焊接计算时间约为2 h,同时,为了对比,针对相同尺寸模型采用移动热源法进行了仿真计算,时间超过24 h。对比发现,应力分区映射法在保证计算精度的同时,大大缩短了计算时间,提高了计算效率。
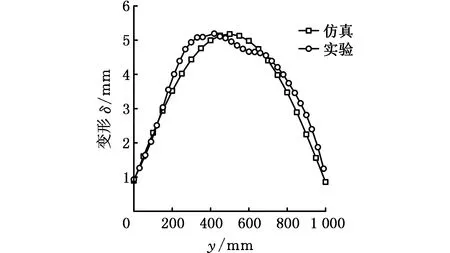
图10 仿真和实验的焊接变形的对比Fig.10 Welding distortion comparison of numerical results and testing data
3.2 焊接变形机理分析
图11为焊接仿真应力云图,图11a为在夹具释放前小模型经过热力分析的应力分布图,考虑边缘效应将小模型的应力分量映射到大模型的焊缝区域,结果如图11b所示。小模型焊缝附近的应力较大,远离焊缝的部位应力几乎为0。焊缝稳态区域的应力分布比较均匀,为350 MPa左右,映射到大模型焊缝处的应力为345 MPa左右。
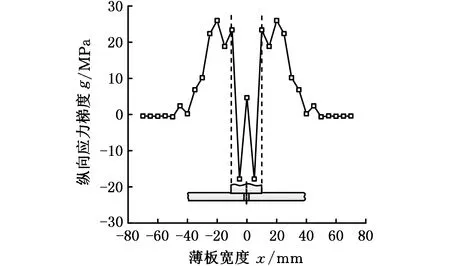
图12 薄板纵向应力梯度Fig.12 Longitudinal stress gradient of thin plate
焊接仿真和实验的变形结果均表明焊后材料出现纵向翘曲变形,主要原因在于焊接过程中,温度沿厚度方向存在明显的梯度,使得夹具释放前焊接件内部存在沿厚度方向的纵向应力梯度。这里将垂直焊缝的截面上表层应力与下表层对应应力相减得到图12所示的沿厚度方向的纵向应力梯度,在轴肩作用区中心及附近很小的范围内,上表层的纵向拉应力略低于下表层的纵向拉应力,得到的应力梯度结果为负值,而在轴肩作用区外更宽的范围内,纵向拉应力的应力梯度为正值,且数值高于负应力梯度,负应力梯度的峰值约为-17 MPa,而轴肩外正应力梯度峰值为25 MPa,由于这部分正的纵向拉应力梯度的存在导致焊接件最终出现纵向翘曲。
3.3 不同拘束距离下的计算结果
取夹具距焊缝的距离即拘束距离L为20 mm、40 mm、60 mm和80 mm,利用上述实验验证的应力分区映射方法进一步讨论不同装夹位置对焊接变形的影响规律。
提取焊缝中间位置即y=500 mm截面的上边线的厚度方向变形曲线,如图13a所示;提取焊缝位置,即x=0截面的上边线的厚度方向变形曲线,如图13b所示。由图13可知,焊接变形在横向和纵向都有明显的非线性变形,从图13a中可以看出垂直焊缝方向曲线呈现下凹,中间焊缝位置变形小于两侧板的边缘变形,并且随着拘束距离的增大,横向变形逐渐增大,距离焊缝较近时,如20 mm和40 mm,变形增加得较大;距离焊缝较远时,如60 mm和80 mm,变形增加得较小。从图13b中可以看出,沿焊缝方向纵向变形呈现上凸变形,焊缝起始端和结束端变形较小,中间部分变形很大,并且随着拘束距离的增大,变形规律与横向变形相同。
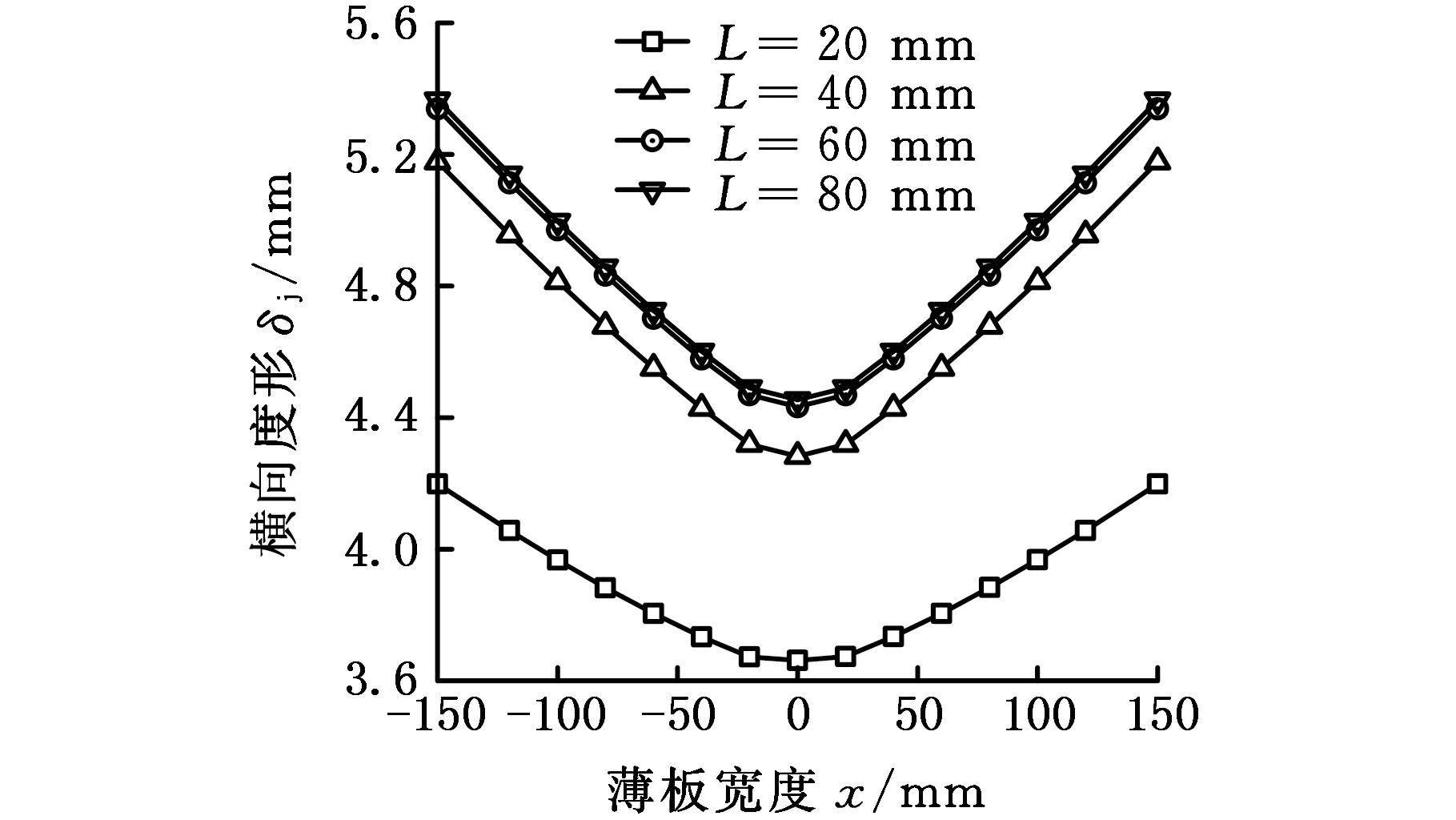
(a)横向变形
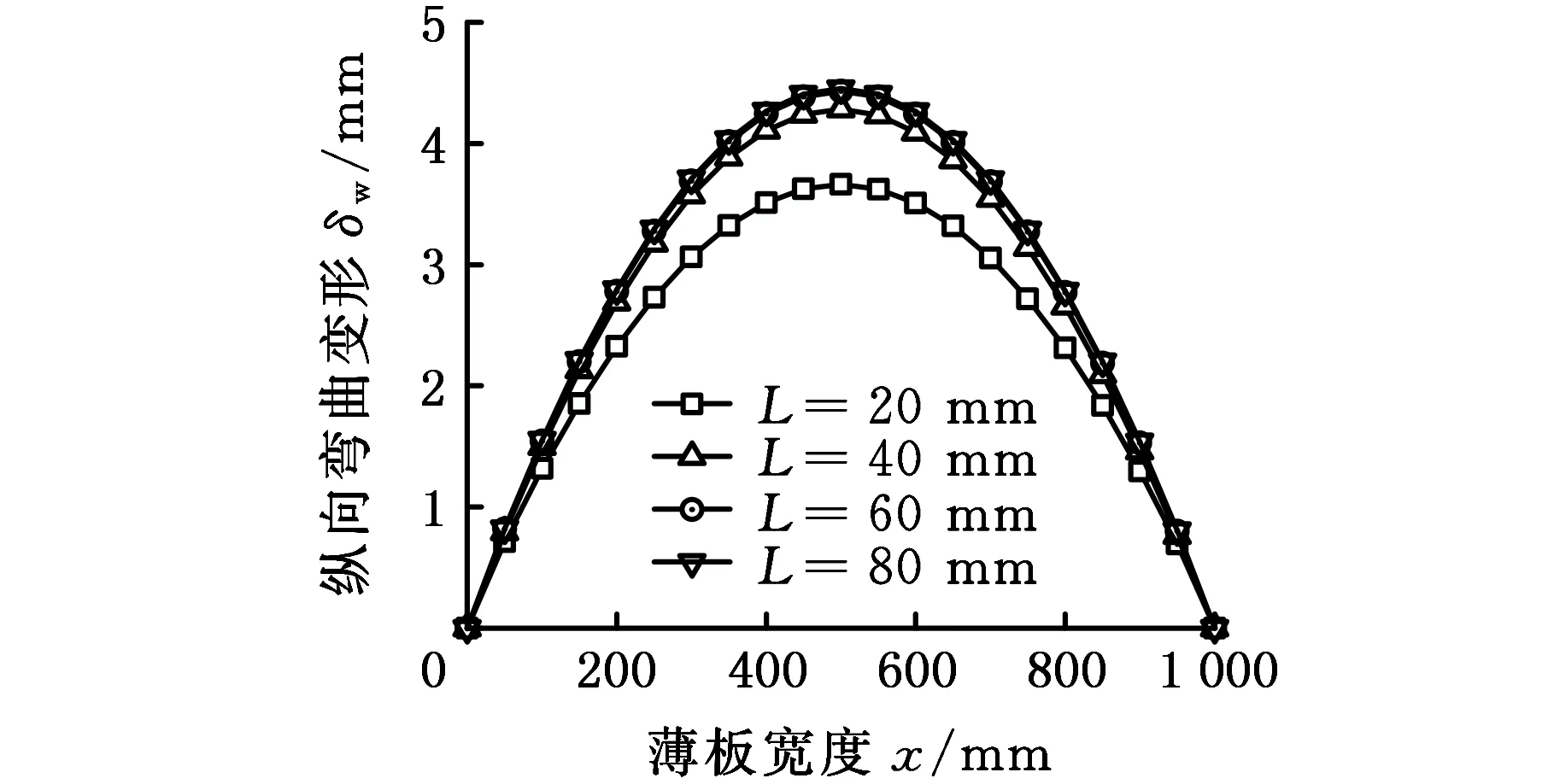
(b)纵向变形图13 整体大模型不同装夹位置下的焊接变形Fig.13 Welding deformation of different clamping constraint by overall large model
图14为最大焊接变形随拘束距离的变化曲线。随着拘束距离的逐渐增大,平板焊接变形呈非线性增大。拘束距离由20 mm增大到80 mm时,最大焊接变形由4.199 mm增大到5.366 mm,增大了约27.8%。由此可见,选取较小的拘束距离,即夹具在距焊缝较近的位置时,对于大尺寸薄壁结构,可以有效地抑制焊接变形。
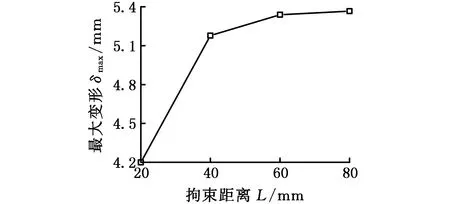
图14 拘束距离对最大焊接变形的影响Fig.14 Impact of restraint distance on the largest welding deformation
由于受夹具拘束距离的影响,结构沿焊缝方向的刚度存在差异,拘束度可以衡量焊接接头刚性的大小。均匀加载时拘束度定义为:使焊接接头根部沿垂直于焊缝方向产生单位弹性位移,单位焊缝长度上所受的力为拘束度。平板焊接拘束度的计算公式如下:
(19)
式中,R为拘束度,N/mm2;Fl为单位焊缝长度上的作用力;S为焊缝不同位置处的单位位移。
根据拘束度定义,沿平板焊缝方向施加垂直于焊缝纵向的均匀载荷进行线弹性静力分析,夹具拘束距离同上。根据计算出的大型薄板结构焊缝处的位移量,提取焊缝位置z向位移量的绝对值,由式(19)计算出结构的拘束度,建立起不同拘束距离下大型薄板结构的拘束度与位置关系曲线,如图15所示。可以看出,薄板焊缝中间稳态区域的拘束度平稳且最大,焊缝起始和结束区域的拘束度变化较大且比稳态区小。并且随着拘束距离从20 mm增大到80 mm,拘束度由343.1 N/mm2减小到53.21 N/mm2,拘束度的减小,表示焊接接头处的刚性减小。夹具越靠近焊缝,焊接过程中对焊缝的拘束度越大,使得焊缝处的刚性也增大,焊缝不易自由收缩,因此焊接变形较小。综上所述,选取较小的拘束距离,可以起到抑制焊接变形的作用。
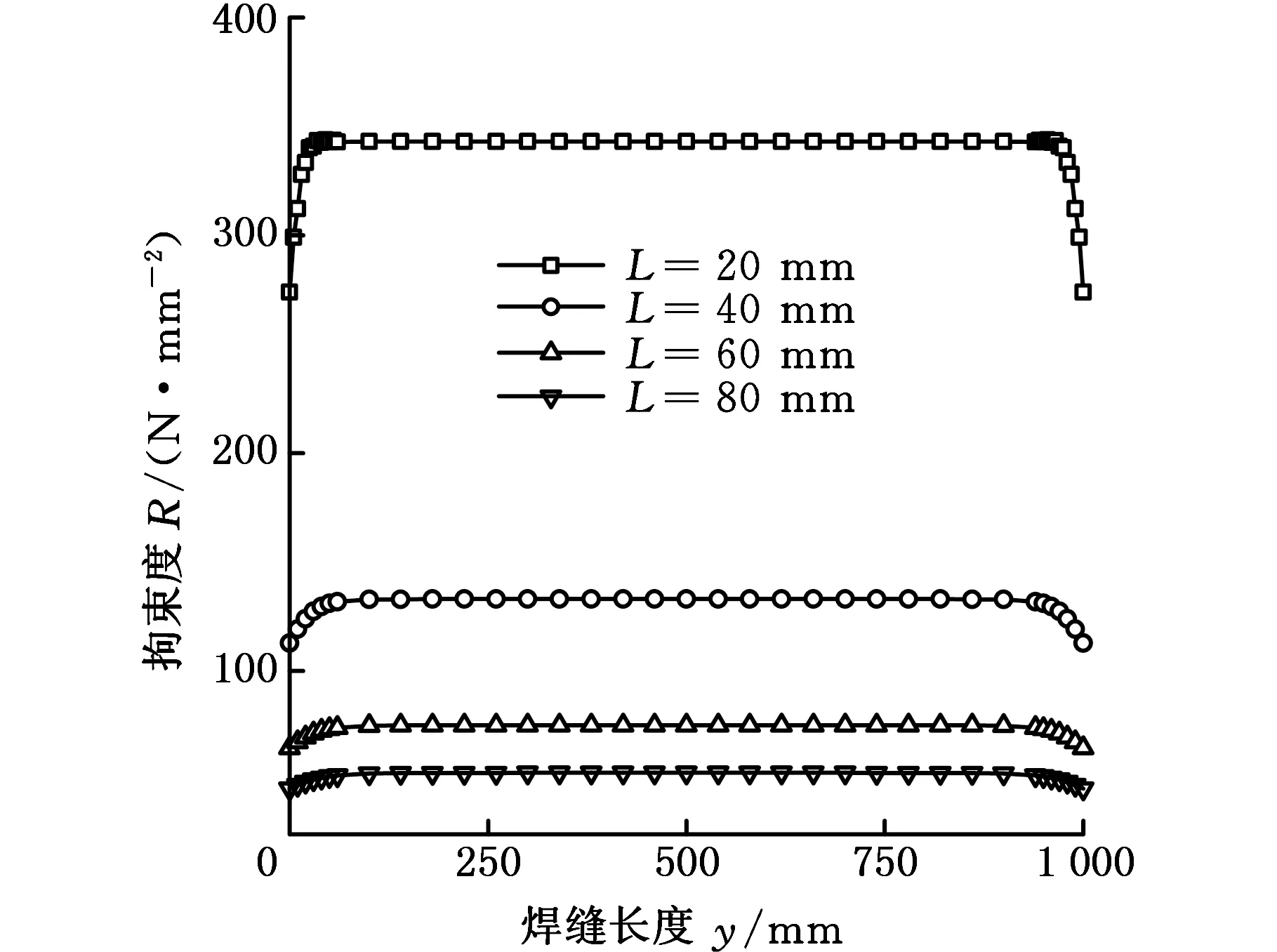
图15 沿焊缝方向的拘束度分布Fig.15 Distribution of restraint intensity along the welding line

图16 不同尺寸模型在不同装夹位置下的焊接变形Fig.16 Welding deformation of different dimension models with different clamping positions
为了探究装夹位置对不同尺寸的模型的焊接变形的影响,计算了平板尺寸为300 mm×2 000 mm×6.8 mm和300 mm×3 000 mm×6.8 mm下的焊接变形。不同尺寸的模型在不同装夹位置下的最大焊接变形结果如图16所示。在焊接平板厚度和宽度不变的情况下,随着焊缝长度的增大,焊接变形也随之显著增大,拘束距离为20 mm时,1 000 mm长的焊缝变形最大值为4.206 mm,2 000 mm长的焊缝变形最大值为16.173 mm,3 000 mm长的焊缝变形最大值为35.912 mm;随着长度的增大,不同的夹具位置对焊接变形的影响也更加显著,随着拘束距离由20 mm增大到80 mm,1 000 mm模型的焊接变形增大了1.167 mm,而3 000 mm模型的焊接变形增大了8.638 mm。综上所述,随着焊接件的尺寸增大,其焊接变形非线性增大,夹具拘束距离对于焊接变形的影响效果更加明显。
4 结论
(1)采用应力分区映射法计算结构焊接变形仿真结果与某一夹具拘束距离下的实验结果相比,相对误差为7.8%,精度达到92.2%,验证了应力分区映射法的正确性。
(2)薄板发生纵向翘曲变形的主要原因在于,焊接过程中,温度沿厚度方向存在明显的梯度,使得夹具释放前焊接件内部存在沿厚度方向的纵向应力梯度。
(3)夹具位置对焊接变形具有重要影响,夹具距焊缝的位置不同,表示对焊缝的拘束程度不同。拘束距离越大,夹具对焊缝的拘束度越小,使得焊缝处的刚度越小,焊接变形越大,因此选取较小的拘束距离可以有效地抑制焊接变形。
(4)随着焊接件尺寸的增大,其焊接变形非线性增大,装夹位置对于焊接变形的影响效果更加明显。
