考虑自锁元件动态特性的超越离合器-齿轮系统模型研究
2019-08-21刘延伟朱云学林子越赵克刚黄谢鑫
刘延伟 朱云学 林子越 赵克刚 黄谢鑫
1.广东工业大学机电工程学院,广州,5100062.华南理工大学机械与汽车工程学院,广州,5106413.广州汽车集团股份有限公司汽车工程研究院,广州,511434
0 引言
超越离合器是一类依靠自锁机制实现动力单向传递的基础机械元件,它根据主从动件相对转速或转向的变化自行实现接合或分离(超越),已被应用于各类机械系统中以实现多种功能。目前,超越离合器的研究工作主要集中在与其应用环境相对应的机构设计及可靠性分析[1-3],基于静力学的应力接触、疲劳寿命及过载能力分析[4-6]以及传动系统的动力学特性[7-9]等方面。
根据建模方法的不同,超越离合器动力学模型分为基于有限元或多体动力学软件的物理模型和数学模型。物理模型多用于研究超越离合器自身特性,数学模型则应用于传动系统的动力学特性研究。在超越离合器数学模型方面,目前广泛采用将主从动端的转角差[8-9]或转速差[10]作为接合或超越状态判据的无转动惯量弹簧阻尼模型。超越离合器的接合是主动件与自锁元件、自锁元件与从动件共同接合作用的结果,由于自锁元件的惯性、变形因素及主从动件之间间隙的存在,超越离合器在接合过程中存在主从动件间的空转角现象[11],即在超越离合器的主从动件达到接合条件后,主从动件之间仍然需要产生一个相对转角(空转角)才能实质上进入接合状态(即传递力矩状态)。虽然超越离合器的同步性能满足上述各类对空转角不严格限制场合的使用要求,但是在动力源或环境的非平稳激励(如发动机转矩周期波动激励、路面振动激励)下,超越离合器处于频繁接合与超越状态的切换过程中,接合空转角对传动系统的动力学特性可能产生明显影响。
随着超越离合器多模式可控化技术的发展,使用超越离合器作为车辆自动变速器换挡控制元件的相关研究工作正在展开[12-14]。更加准确地描述超越离合器的动力学特性,提高其数学模型的精度,可以为超越离合器及其系统传动链的动态特性研究形成更好的支撑。本文在传统超越离合器动力学数学模型的基础上,提出通过转角补偿的形式将自锁元件动态特性的影响纳入建模的考虑因素,建立了不同类型的超越离合器-齿轮系统动力学模型,分别在输入端驱动力矩稳定和波动两种情况下,应用MATLAB/Simulink进行动力学特性仿真计算,并进行了超越离合器-齿轮系统台架试验,对计算结果和试验结果进行了对比分析。
1 动力学模型
1.1 超越离合器模型
传动系统动力学特性的研究以各部件数学模型为基础。可控超越离合器应用于汽车传动系统时通常布置于齿轮与轴之间,实现动力通断控制功能。将传动系统各部件简化为无弹性阻尼的惯量环节和无惯量的弹性阻尼环节,超越离合器的主从动端分别与轴或齿轮惯量刚性连接,当超越离合器处于接合状态时,将超越离合器本体视为一个无惯量的弹性阻尼体;当超越离合器处于超越状态时,动力传递中断。超越离合器输入端和输出端的转速差或转角差被普遍作为其数学模型中工作状态的判断依据,形成的模型在本文中分别称为“转速差模型”和“转角差模型”。转速差模型和转角差模型下超越离合器传递转矩Mc(t)的表达式分别如下:
(1)
(2)
式中,Kc为超越离合器扭转刚度,N·m/rad;Cc为超越离合器阻尼系数;θm(t)为主动端扭转角度,rad;θs(t)为从动端扭转角度,rad。
式(1)和式(2)并未考虑超越离合器自锁元件动态特性对接合过程的影响。
传动系统在工作过程中往往受到动力源或负载的非平稳激励(如汽车发动机周期波动激励或路面振动激励),超越离合器若处于主传动链当中,其工作状态也随着非平稳激励处于接合→超越→接合的频繁切换过程中。如图1所示,以θm(t)和θs(t)表示在t时刻超越离合器主动端和从动端所转过的角度,随着状态切换次数的不断增加,式(1)和式(2)中弹性力分量Kc(θm(t)-θs(t))不断变大,这与实际情况不符,为研究超越离合器及其传动系统的动力学特性带来了困扰。

图1 转角差累积示意图Fig.1 The rotational angle discrepancy accumulation diagram
考虑自锁元件动态特性对接合过程的影响,本文提出以转角补偿形式抵消累计空转角差的设想。基于转速差模型的转角补偿Δθαv(t)为
(3)
带转角补偿的转速差模型为
(4)
基于转角差模型的转角补偿Δθα(t)为
Δθα(t)=
(5)
带转角补偿的转角差模型为
(6)
1.2 系统模型
建立图2所示的超越离合器-齿轮副系统的动力学模型。其中,I为转动惯量,kg·m2;θ(t)为扭转角度,rad;r为齿轮基圆半径,m;T为扭矩,N·m;下标i、1、2、o分别表示输入端、齿轮1、齿轮2、输出端;K(t)为齿轮副的时变啮合刚度,N·m;C为齿轮副的啮合阻尼系数;b为齿轮单侧间隙。

图2 超越离合器-齿轮副系统动力学模型Fig.2 Overrunning clutch-gear system dynamics model
以输入端(包括超越离合器主动端)、齿轮1(包括超越离合器从动端)、齿轮2部件为惯量环节,超越离合器接合和齿轮啮合简化为无惯量的弹性阻尼环节,阻尼系数的计算和取值参考文献[7]确定,推导出该系统的运动微分方程如下:
(7)
式中,β(t)为啮合齿轮副齿侧间隙的非线性函数;K(t)为齿轮副的时变啮合刚度,采用文献[15]中提出的多阶拟合刚度模型确定。
2 仿真对比及分析
2.1 仿真模型的建立
根据式(1)~式(7),分别在MATLAB/ Simulink中建立相应的仿真模型。模型中主要参数如表1所示[16]。
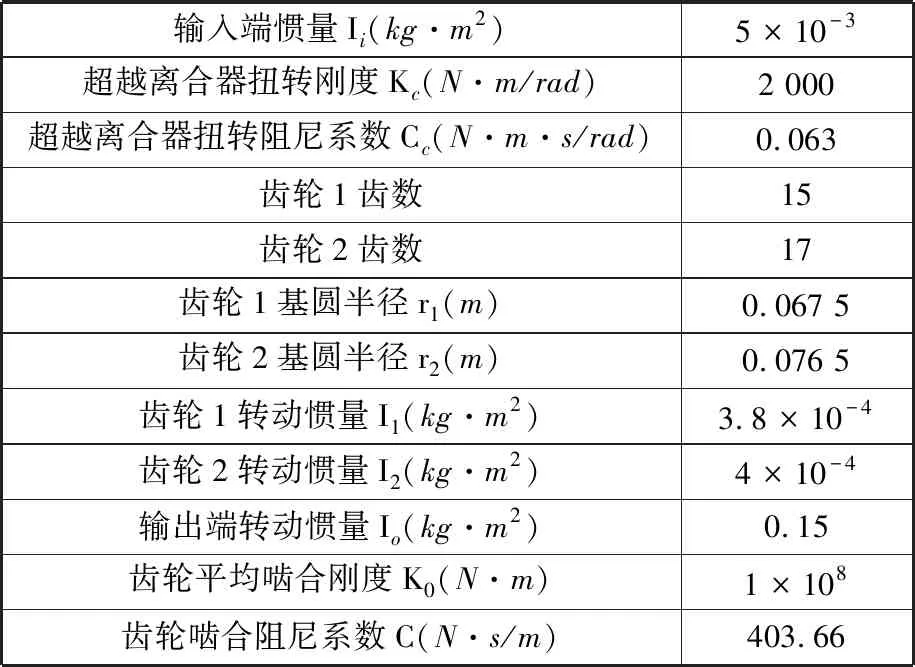
表1 超越离合器-齿轮系统的仿真参数Tab.1 The simulation parameters of overrunning clutch-gear system
为了对文中4种超越离合器模型进行全面的对比分析,分别在驱动力矩稳定和波动两种典型工况下完成超越离合器-齿轮系统的动力学特性仿真计算。
2.2 驱动力矩稳定工况
设定超越离合器-齿轮系统的初速度为35 rad/s,输入端扭矩Ti为15 N·m,输出端扭矩To为-17 N·m,仿真结果如图3~图6所示。
图3a中,纵坐标y值为1代表超越离合器处于接合状态,y值为0代表处于超越状态(其余各模型相同)。在0~0.01 s时间段内,超越离合器处于接合状态。在0.01~0.3 s时间段内,超越离合器工作状态在接合和超越之间反复切换。图3b显示,在0~0.01 s时间段内,超越离合器传递力矩线性增大,在0.01~0.3 s时间段内,由于两种状态的不断转换,力矩快速跳变,力矩值随时间延长呈现增大趋势。图3c显示,在0~0.01 s时间段内,在驱动力矩和负载力矩作用下,输入端角速度增大,输出端角速度减小,在0.01~0.3 s时间段内,输入端角速度减小,输出端角速度增大,随后以±0.5 rad/s的波动振荡。图3d显示,输入、输出端转角线性增大。
图4a显示,接合、超越状态周期性切换,且超越的时间很短。图4b显示,接合状态下传递力矩不断增大,超越状态下传递力矩为0。图4c显示,输入、输出端角速度均呈现较大幅度波动。图4d显示,输入、输出端转角线性增长。

(a)超越离合器接合状态
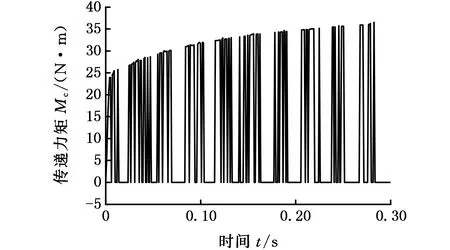
(b)超越离合器传递力矩
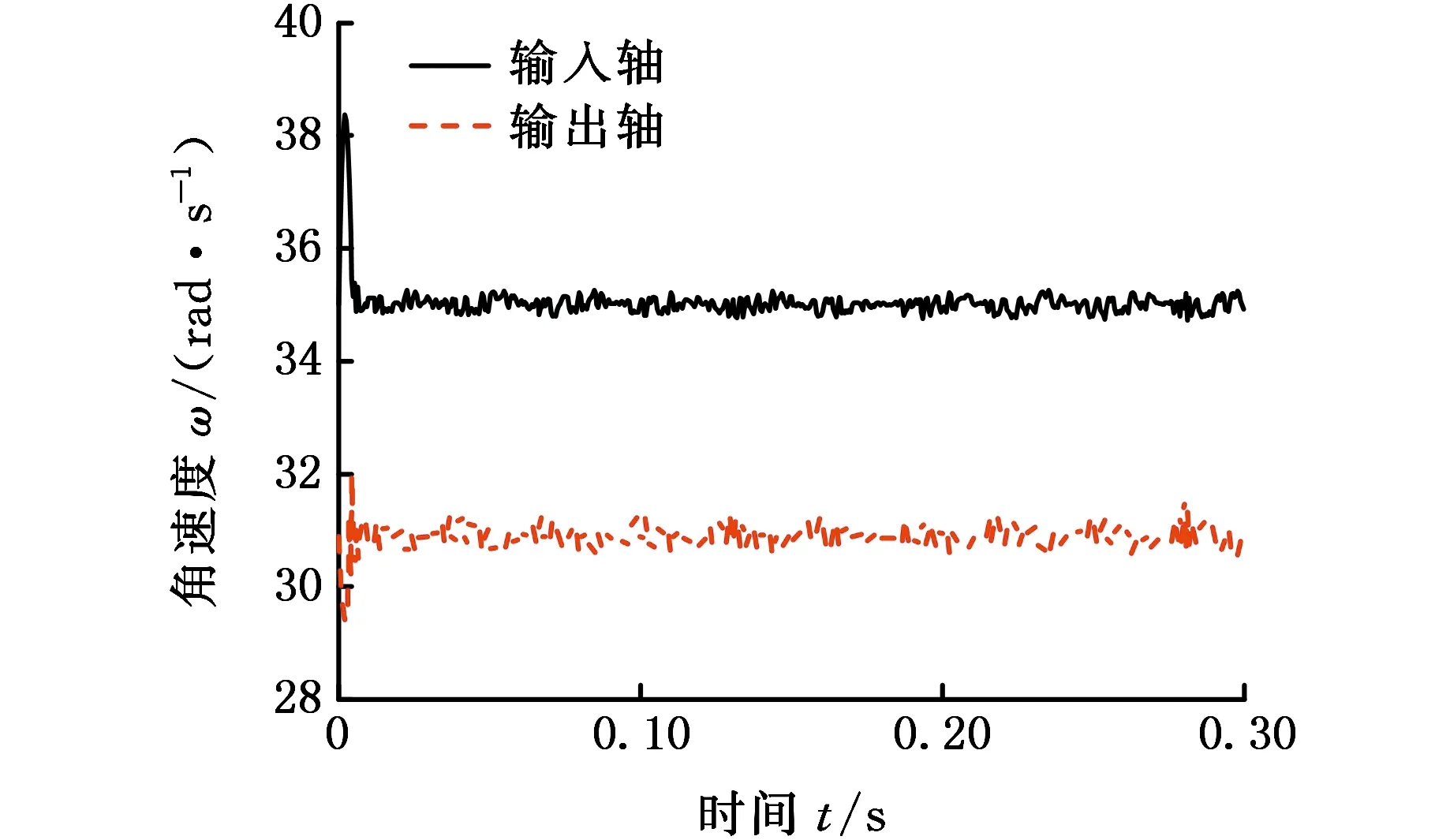
(c)输入轴和输出轴角速度

(d)输入轴和输出轴转角图3 驱动力矩稳定工况下角速度差模型的仿真结果Fig.3 Simulation result of the angular velocity discrepancy model with constant torque
图5a显示,超越离合器始终处于接合状态。图5b显示,在0~0.025 s时间段,传递力矩从0振荡增长到15 N·m,之后以±2 N·m幅度振荡。图5c显示,在超越离合器接合瞬间,输入端角速度发生较大波动,随后逐渐稳定在35 rad/s左右,输出端角速度与输入端角速度变化规律相似,波动后逐渐稳定在31 rad/s左右。图5d显示,输入、输出端转角线性增长。图6的仿真结果与图5基本一致。

(a)超越离合器接合状态

(b)超越离合器传递力矩

(c)输入轴和输出轴角速度
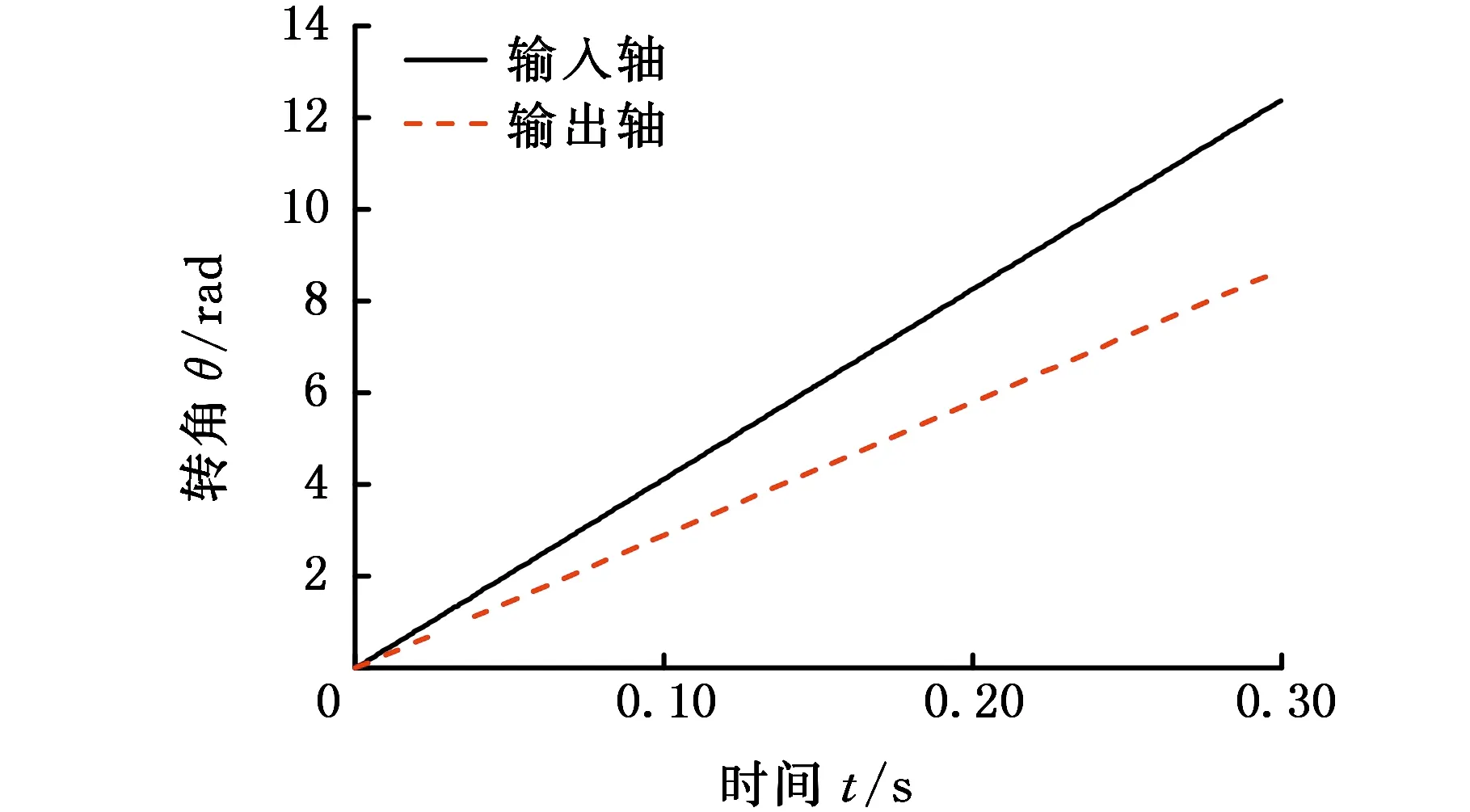
(d)输入轴和输出轴转角图4 驱动力矩稳定工况下带有转角补偿的角速度差模型的仿真结果Fig.4 Simulation result of the angle compensation angular velocity discrepancy model with constant torque
对比分析图3~图6中各图的a图所示的超越离合器工作状态发现,以转速差作为超越离合器工作状态判断依据的转速差模型和带有转角补偿转速差模型均显示,在整个过程中,超越离合器工作状态在超越和接合之间反复切换。以转角差作为超越离合器状态切换的判断依据的两类模型显示,在整个过程中,超越离合器的工作状态一直稳定处于接合状态。

(a)超越离合器接合状态

(b)超越离合器传递力矩

(c)输入轴和输出轴角速度

(d)输入轴和输出轴转角图5 驱动力矩稳定工况下转角差模型的仿真结果Fig.5 Simulation result of the rotational angle discrepancy model with constant torque
观察图3~图6中超越离合器所传递的转矩发现,与在接合和超越状态之间反复切换相对应,两类转速差模型反复振荡波动,带有转角补偿转速差模型波动范围更大。与稳定处于接合状态相对应,两类转角差模型保持平稳,反映了真实的转矩传递情况,而转角补偿的加入与否对传递转矩的计算并未产生明显的影响。
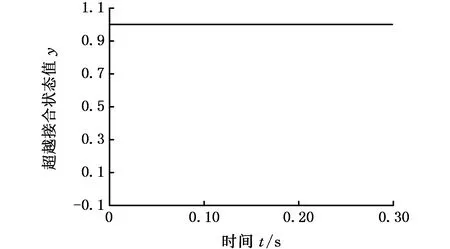
(a)超越离合器接合状态
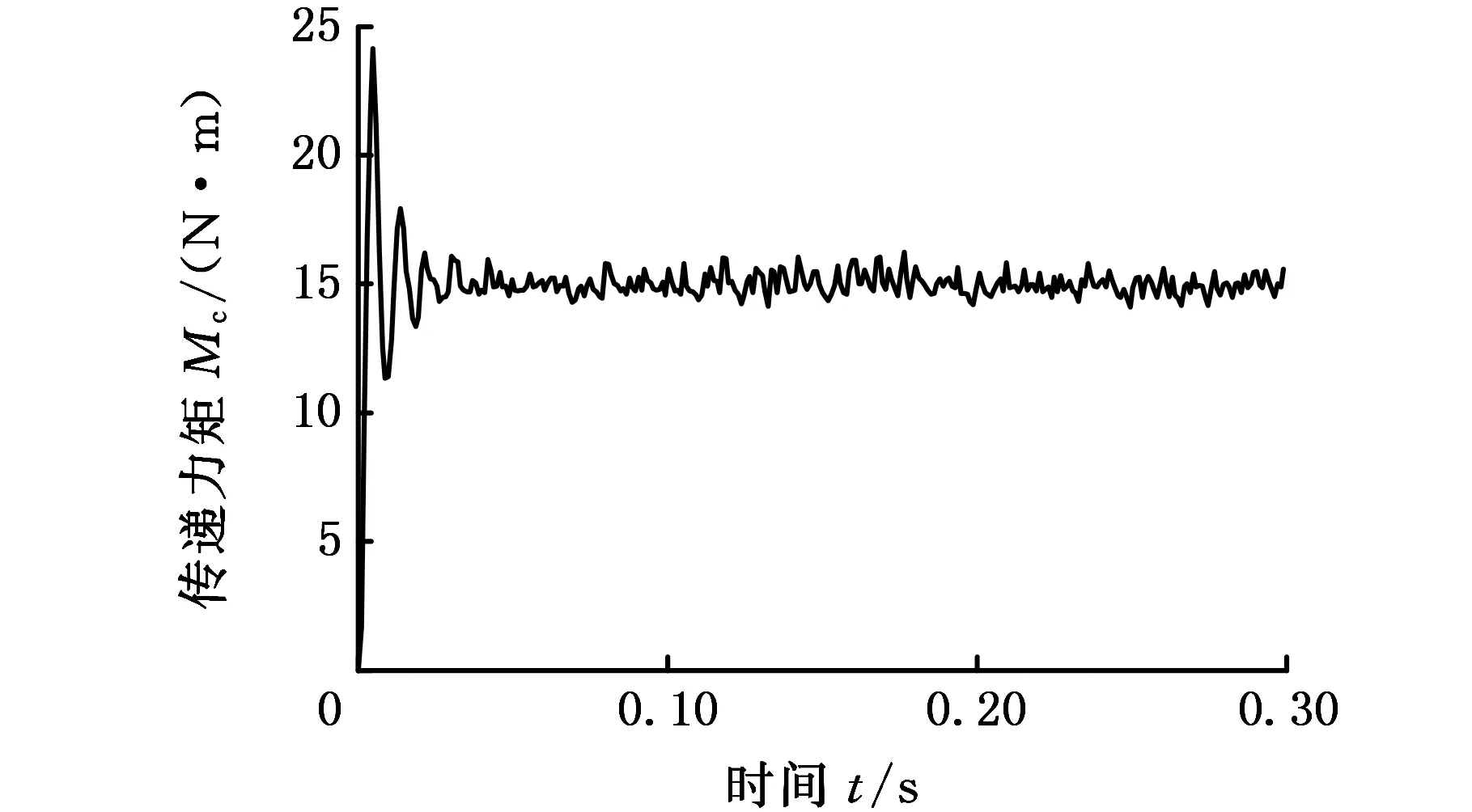
(b)超越离合器传递力矩

(c)输入轴和输出轴角速度
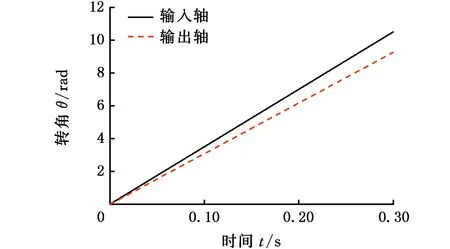
(d)输入轴和输出轴转角图6 驱动力矩稳定工况下带有转角补偿的转角差模型的仿真结果Fig.6 Simulation result of the angle compensation rotational angle discrepancy model with constant torque
观察图3~图6各图中c图和d图的系统输入轴、输出轴角速度和转角发现,相比较于转速差模型,带有转角补偿转速差模型的输入轴和输出轴角速度均出现了较大幅度的振荡,输入轴转角也明显变大,转速差模型、转角差模型和带有转角补偿转角差模型计算得到的输入轴、输出轴转角未表现出明显的差异。
2.3 驱动力矩波动工况
超越离合器具有正转矩接合、负转矩超越(分离)的工作特性,为了更清晰地对比分析各类模型的有效性,设定驱动力矩在正负转矩间波动[9]。设定超越离合器-齿轮系统的初速度为35 rad/s,Ti=15+30 sin(20πt)N·m,To为-17 N·m,分别得到各类模型的仿真结果,如图7~图10所示。
图7a显示,在0~0.01 s时间段内,超越离合器处于接合状态。在0.01~0.065 s时间段内,工作状态在接合和超越之间反复切换。在0.065~0.1s时间段内,始终都是超越状态。0.1~0.2 s和0.2~0.3 s两个时间段内,工作状态均是先反复切换,然后保持超越状态。图7b显示,在0~0.065 s、0.1~0.165 s和0.2~0.265 s三个时间段内,由于两种状态的不断转换,力矩快速跳变,在后两个时间段内力矩最大值已超过500 N·m,在0.1 s和0.2 s左右有一个较大的负力矩。图7c显示,输入端角速度随力矩的波动而波动,在0.065~0.1 s、0.165~0.2 s和0.265~0.3 s时间段内,输入端角速度低于输出端角速度,超越离合器处于超越状态。在0.1 s和0.2 s时刻,输入端角速度出现正向跳动,输出端角速度出现负向跳动。图7d显示,输入、输出端转角均呈曲线增长。
图8a显示,在0~0.065 s时间段内超越离合器基本处于接合状态,在0.065~0.1 s时间段内保持超越状态,随后重复出现0~0.1s间的状态变化。图8b显示,接合状态下传递力矩不断增大,超越状态下传递力矩为0。图8c显示,在输入、输出端角速度增大阶段,呈现锯齿状波动,在角速度下降阶段,输出端角速度大于输入端角速度。图8d显示,输入、输出端转角均呈曲线增长。
图9a显示,0~0.065 s超越离合器处于接合状态,0.065~0.12 s超越离合器处于超越状态,在0.12~0.16 s进行多次状态切换,而0.16~0.22 s时间段又重新处于超越状态,之后重复0.12~0.22 s的状态变化。图9b显示,工作状态从超越状态切换到接合状态时,会出现较大的正力矩;而从接合状态切换到超越状态时,则会出现负力矩。图9c显示,工作状态从超越状态切换到接合状态时,输入端和输出端角速度均出现较大波动。图9d显示,输入、输出端转角均呈曲线增长。

(a)超越离合器接合状态

(b)超越离合器传递力矩

(c)输入轴和输出轴角速度

(d)输入轴和输出轴转角图7 驱动力矩波动工况下转速差模型仿真结果Fig.7 Simulation result of the rotational speed discrepancy model with varying torque
图10a显示,0~0.065 s超越离合器处于接合状态,在0.065 s附近出现状态切换,0.065~0.1 s处于超越状态,后续时间重复0~0.1s的状态变化。图10b显示,接合状态下力矩先增大后减小,超越状态下力矩为0。图10c显示,接合状态下,输入、输出端角速度跟随驱动力矩规律变化;超越状态下,由于驱动力矩为负值,输入端角速度相对输出端角速度下降得更快。在0.1 s附近,随着超越离合器从超越状态切换到接合状态,由于超越离合器具有刚度阻尼特性,出现了微小的角速度波动。由图10d可见,输入、输出端转角均呈曲线增长。

(a)超越离合器接合状态

(b)超越离合器传递力矩

(c)输入轴和输出轴角速度

(d)输入轴和输出轴转角图8 驱动力矩波动工况下带有转角补偿的转速差模型仿真结果Fig.8 Simulation result of the angle compensation rotational speed discrepancy model with varying torque

(a)超越离合器接合状态

(b)超越离合器传递力矩

(d)输入轴和输出轴转角图9 驱动力矩波动工况下转角差模型仿真结果Fig.9 Simulation result of the rotational angle discrepancy model with varying torque
观察图7~图10各图中a图的超越离合器工作状态发现,随着驱动力矩的波动,各类模型均显示在整个过程中超越离合器发生了多次接合和超越状态的交替,转速差模型、带有转角补偿的转速差模型和转角差模型均在驱动力矩为正值时,出现接合-超越状态交替的现象,带有转角补偿的转角差模型在驱动力矩为为正值时,保持接合状态,在驱动力矩为负值时,进入超越状态。

(a)超越离合器接合状态

(b)超越离合器传递力矩
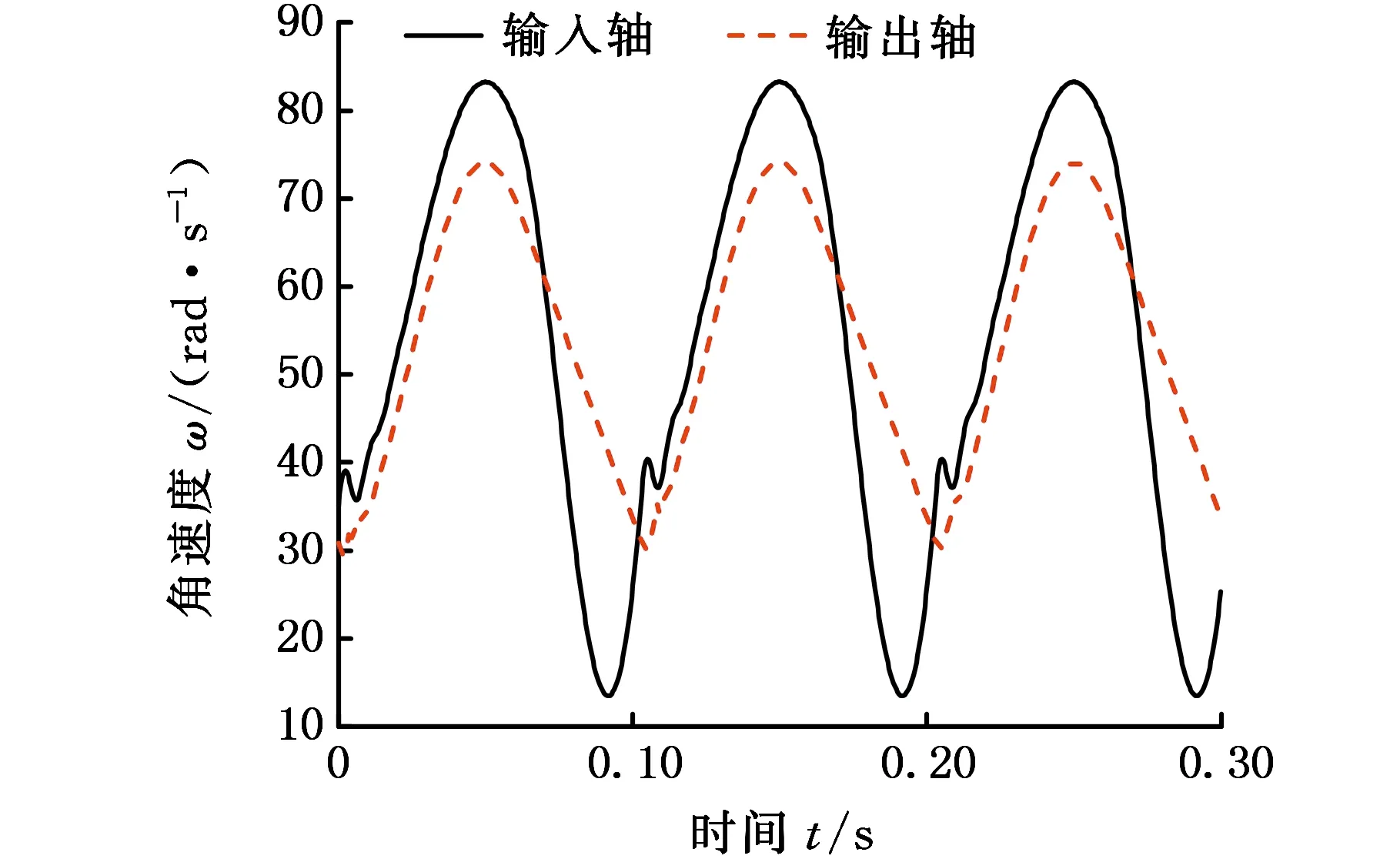
(c)输入轴和输出轴角速度

(d)输入轴和输出轴转角图10 驱动力矩波动工况下带有转角补偿的转角差模型仿真结果Fig.10 Simulation result of the angle compensation rotational angle discrepancy model with varying torque
观察图7~图10各图中b图的超越离合器传递转矩发现,转速差模型和转角差模型波动幅度很大,并出现了明显的负值,这与超越离合器的工作特性相违背,反映出这两类模型在驱动转矩波动的工况下不能准确表达超越离合器的动力学特性。加入转角补偿的转速差模型呈现高频和大幅波动,加入转角补偿的转角差模型较为稳定。
对比分析图7~图10各图中c图和d图的系统输入轴、输出轴角速度和转角发现,转速差模型和转角差模型都出现了角速度突变,加入转角补偿的转速差模型伴随其驱动转矩的高频和大幅波动出现了锯齿状波动,加入转角补偿的转角差模型较为稳定。
3 实验对比及分析
基于驱动力矩稳定和波动两种工况下仿真结果的对比分析,初步得到带有转角补偿的转角差模型能够较为准确地描述超越离合器动力学特性的判断,为了进一步验证这一判断,搭建了超越离合器-齿轮系统的传动实验台架。该传动实验台架由驱动电机、超越离合器-齿轮系统、转动惯量和负载以及相应的控制和测量装置组成。传动实验台架的示意图和现场照片见图11,台架机械部分结构组件的参数如表2所示。实验台通过高性能闭环矢量变频器控制电机的转速恒定或波动,通过张力控制器对磁粉制动器进行控制,实现负载端力矩保持恒定,旋转编码器分别测得输入轴、输出轴的转速。

1.电机 2.联轴器 3.旋转编码器 4.超越离合器-齿轮副机构 5.惯量飞轮 6.制动器(a)实验台架示意图

(b)实验台实物图图11 超越离合器-齿轮系统传动实验台Fig.11 Transmission experimental bench of overrunning clutch-gear system

1TL0001-0EB4三相异步电机额定功率(kW)1.5FZ 10. J磁粉制动器最大转矩容量(N·m)10转动惯量(kg·m2 )电机0.004 7惯性飞轮10.022 4惯性飞轮20.022 4
基于所搭建的实验台,分别进行了输入端转速稳定和波动两种工况下的实验,在传动台架运行一段时间达到相对稳定状态后进行转速信号的采集。与实验中达到相对稳定状态相对应,取t=0.05 s后上述各类模型转速计算结果相对稳定部分的数据进行对比。由于超越离合器-齿轮系统传动比是17∶15,为了便于进行对比分析,将实验和模型仿真计算得到的输出轴转速乘以传动比,处理后的实验结果分别如图12和图13所示,仿真计算结果分别如图14和图15所示。

图12 转速稳定工况下输入轴和输出轴转速的实验结果Fig.12 Experimental results of input shaft and output shaft rotational speed under stable speed condition

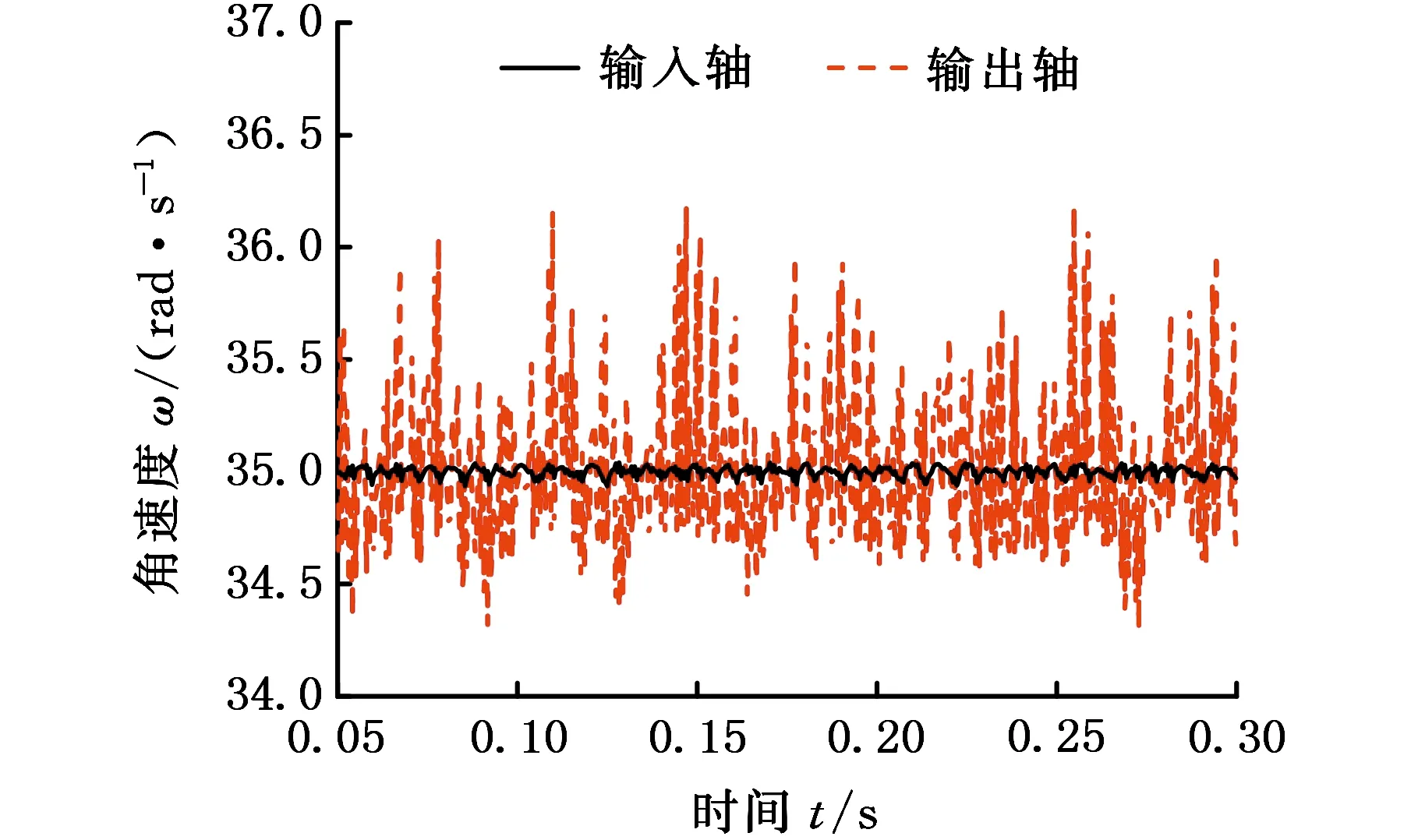
图13 转速波动工况下输入轴和输出轴转速的实验结果Fig.13 Experimental results of input shaft and output shaft rotational speed under fluctuant speed condition

(a)转速差模型
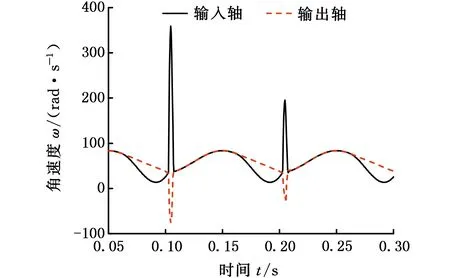
(b)转角差模型

(c)带有转角补偿的转速差模型

(d)带有转角补偿的转角差模型图14 各类模型在驱动力矩稳定工况下角速度仿真结果Fig.14 Simulation results of angular velocity under constant driving torque of each model
(a)转速差模型

(b)转角差模型

(c)带有转角补偿的转速差模型

(d)带有转角补偿的转角差模型图15 各类模型在驱动力矩波动工况下角速度仿真结果Fig.15 Simulation results of angular velocity under varying driving torque of each model
由图12可见,在输入端转速稳定工况下,超越离合器机构输入轴和输出轴转速均相对稳定于750 r/min,由于所搭建的实验台架存在振动问题,使得输入轴和输出轴的转速以±50 r/min的振幅振荡。在相同工况下,图14所示的转速差模型(图14a)、转角差模型(图14b)和带有转角补偿的转角差模型(图14d)计算得到的角速度曲线趋势均与实验结果比较接近,带有转角补偿的转速差模型(图14c)角速度波动比较大,且输入端与输出端角速度存在明显的角速度差,与实验结果相差较远。
图13所示为转速波动工况下输入轴和输出轴转速的实验结果,在1~3 s和5~7 s时间段内,输入端转速明显低于输出端转速,即超越离合器出现了明显的超越现象。在1 s左右输入轴转速开始减小的瞬间,输入轴和输出轴并未立即表现出明显的转速的差异,这体现出了自锁元件的动态特性,也说明了实验结果的有效性。图15中,采用转速差模型(图15a)在0.1 s和0.2 s左右超越离合器从超越状态进入接合状态时,输入端和输出端角速度均发生了较大的波动,明显与实验结果不符。采用转角差模型(图15b),在0.1 s和0.2 s左右超越离合器从超越状态进入接合状态时,输入端角速度发生了很大的波动,与实验结果相差较大。带有转角补偿的转速差模型(图15c)在角速度增大阶段,输入端和输出端角速度出现多次波动,且波动范围比较大,与实验结果不相符。带有转角补偿的转角差模型(图15d)角速度变化趋势与实验结果较吻合。实验结果验证了带有转角补偿的转角差模型能够较为准确地描述超越离合器动力学特性的判断。
4 结论
综合文中的仿真和实验对比分析可得:以转速差作为超越离合器工作状态判断依据,不能准确判断传动系统中超越离合器的实际工作状态;以转角差作为超越离合器工作状态判断依据,只能在传动系统转速稳定的情况下准确判断超越离合器的实际工作状态。
本文的研究工作表明,在转角差模型的基础上通过转角补偿的形式将自锁元件动态特性的影响纳入建模的考虑因素,在传动系统转速稳定和波动的情况下,都能够准确判断超越离合器的实际工作状态,并能够更为准确地描述带有超越离合器传动系统的动态特性。
