发射燃气扩散过程数值模拟及安全性分析

孙伟，杨培源

（91550 部队 41 分队，辽宁 大连 116023）

飞行器弹射时，提供动力的燃气发生器会产生大量高温、高压、高速燃气，其中包含了大量Cl2、NO、NO2等有毒气体，还伴随有金属或金属化合物颗粒[1]，会严重威胁阵地周围操作人员的健康。分析发射燃气的扩散规律、覆盖范围，对提高作战能力，保障操作人员安全具有重要意义。

数值模拟是研究气体扩散问题的主要手段，目前已有上百种适用于气体扩散的数学模型和一系列计算软件，其中CFD 方法及FLUENT 软件应用最广。当前应用于气体扩散模拟的CFD 模型主要是雷诺平均模拟（RANS）和大涡模拟（LES）。RANS 模型精度高，计算量较低，在工业界应用广泛。LES 模型的数据分辨率高于RANS，计算更大，是近年来发展迅速的湍流模拟方法[2]。蒋德海等[3]采用RANS 模型对城市街道内的污染物扩散进行了模拟，分析了决定街道峡谷内污染物质量浓度分布的因素。崔桂香等[4]使用LES 方法对小区内的污染物扩散进行了数值模拟，结果与实际测量十分接近。席学军等采用LES 方法，对复杂山区内高含硫井井喷气体扩散进行模拟，分析了不同风速、风向及地形对气体扩散的影响，给出了划分安全距离的方法[5]。FLUENT 软件功能强大，集成了包括RANS、LES 在内的多种湍流模型，可以满足复杂地形等多种条件下的流场模拟、定常与非定常计算[6]，在气体扩散方面应用广泛。刘增苹等[7]基于FLUENT 三维瞬态流动的原理，模拟了有毒气体绕障碍物的扩散过程，得到了有毒气体扩散及伤害区域分布的一般规律。邵毅等[8]用FLUENT 对榆中县城区的流场和污染物扩散形态及规律进行了模拟研究，得到的结果与实验数据具有较好的一致性。文中采用CFD方法结合FLUENT 软件模拟燃气发生器产生的有毒气体，在风、山地等因素影响下的扩散过程，分析其对周边安全的影响。

1 控制方程

1.1 基本假设

基于以下假设建立方程：把有毒气体的扩散过程看作是不可压缩流运动，所有气体均为理想气体，遵守理想气体状态方程；忽略热损失，不考虑燃烧及气体间的化学反应；不考虑多相流，忽略燃气中的固体颗粒和液体。

1.2 基本方程

1）连续性方程：

式中：ρ 为混合物密度；uj为x、y、z 三个方向上的速度。考虑混合气体不可压，密度ρ 为常数，则式（1）可变为：

2）动量守恒方程：

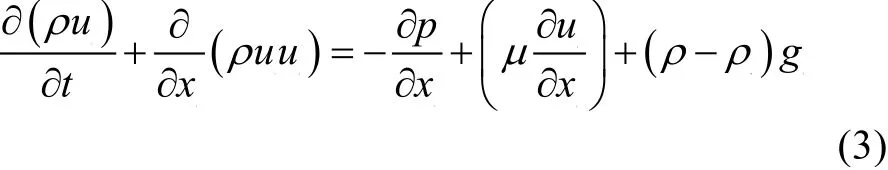
式中：μ 是流体的动力黏度；g 是重力加速度；p是绝对压力；ρa是空气密度。

3）组分质量守恒方程：

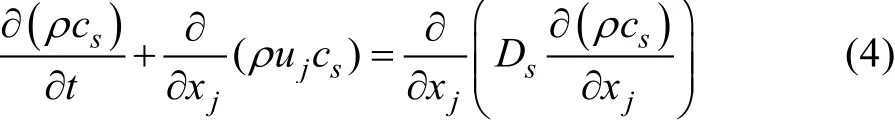
式中：cs为组分s 的体积浓度；ρcs是该组分的质量浓度；Ds是该组分的扩散系数[9]。

4）湍流方程。采用得到RNG k-ε 湍流模型，通过在大尺度运动和修正后的黏度项体现小尺度的影响，而使小尺度运动有系统地从控制方程中去除。所以得到k 方程和ε 方程为[10]：

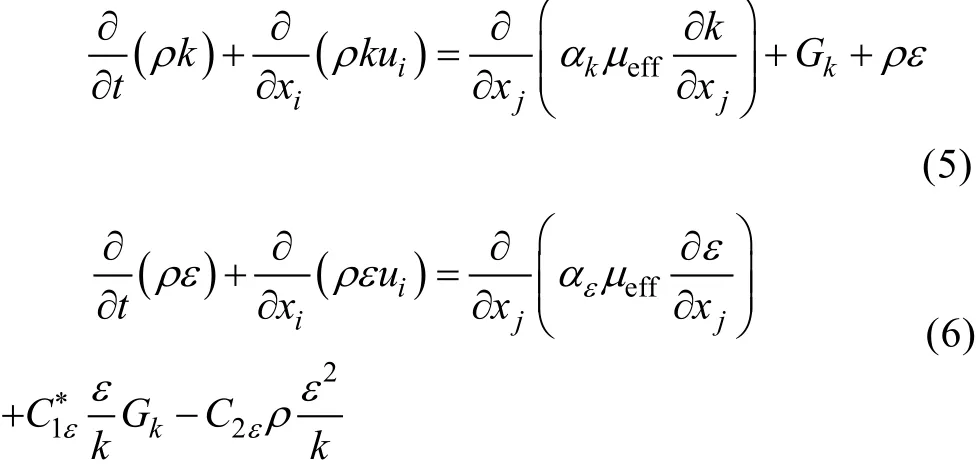
2计算步骤

2.1 网格模型

在DEM 高程图上截取1 km×0.6 km 的矩形区域，保存为海拔高程数据，如图1 所示。将海拔高程数据导入Geomagic Studio 逆向工程软件，经过拟合处理后，进行网格划分。发射阵地的选择分别为山顶和山底，建立一个高10 m，直径2 m 的发射筒。坐标系的选择：原点为发射筒底面圆心，x 轴沿风的来流方向，y 轴竖直向上，z 轴符合右手法则。计算区域沿y轴的远场范围设为200 m。在进行网格划分时，发射筒附近应当加密，而后向其他方向逐渐稀疏。网格单元总量为97 万。两种不同位置发射阵地的网格划分如图2、图3 所示。

图1 山地DEM 图截取

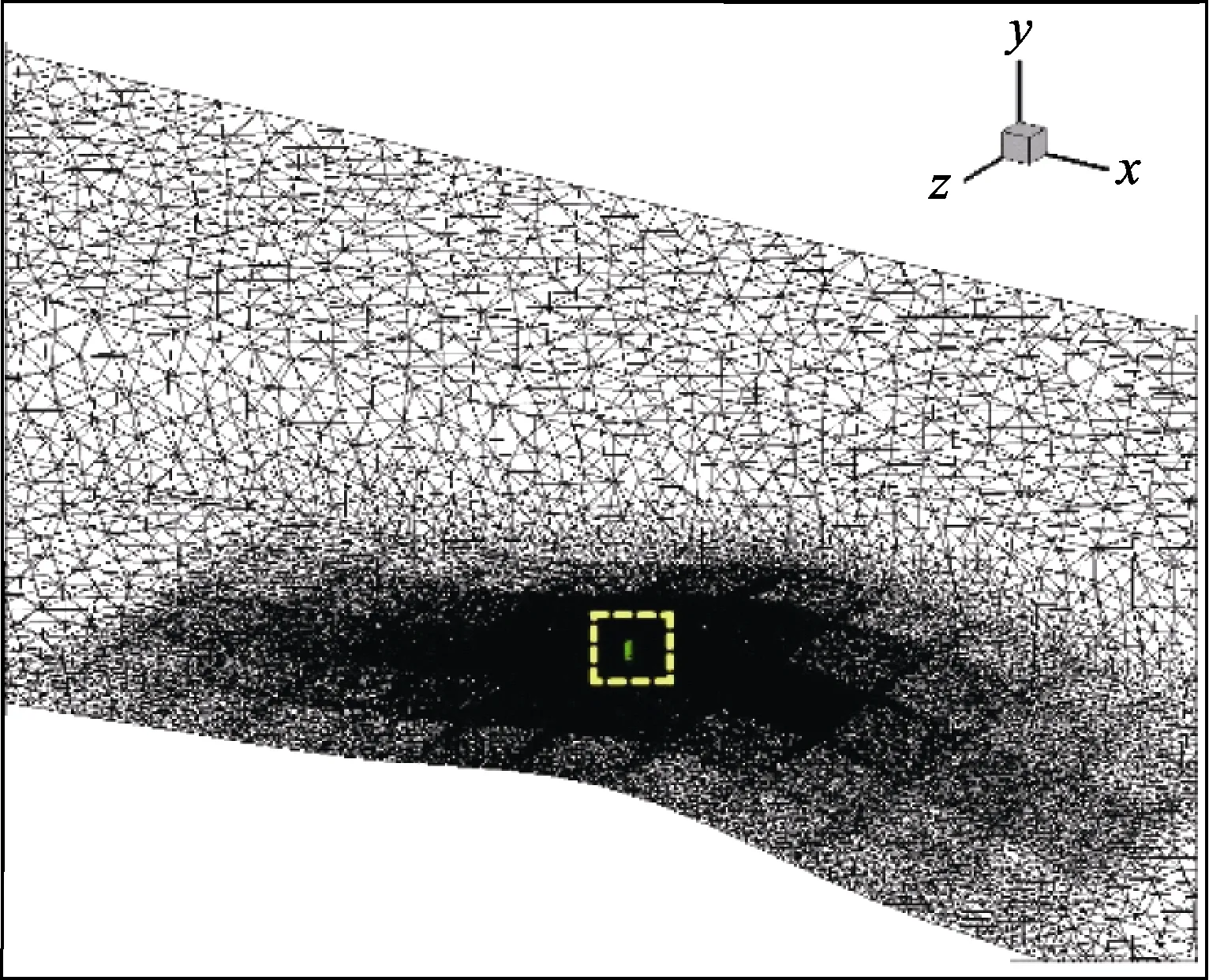
图2 山顶发射阵网格

图3 山底发射阵网格

2.2 参数设置与边界条件

火工品采用含高氯酸铵的CTPB，其快速燃烧后可产生245 kg/s 的质量流量，工作时间为1 s，燃烧温度3000 K，定压比热CP=1800 J/(kg·K)[1,11]。发射燃气为多种气体混合物，其相对空气密度的大小会影响气体的扩散性。选用氯气（Cl2）作为研究对象，密度是空气的2.45 倍。氯气属于剧毒气体，氯浓度过高或接触时间较久，会致使深部呼吸道病变、细支气管及肺泡受损、肺炎及中毒性水肿；高浓度氯吸入后，还可刺激迷走神经，引起反射性的心跳停止[1]。氯气体积分数为1×10-6～3×10-6时（短时间内允许），会引起轻微的黏膜刺激；体积分数为5×10-6～15×10-6时，将引起中度的上呼吸道刺激；体积分数为30×10-6时，会引起突发性咳嗽、胸痛、呕吐；体积分数为40×10-6～60×10-6时，会引起中毒性肺炎，肺水肿；体积分数为430×10-6时，人体暴露30 min 将导致死亡。根据氯气对人体伤害情况[12]，文中考察的氯气最低体积分数为30×10-6。

计算6 种风速下的污染物扩散情况，分别为0、2、5、10、15、18 m/s，空气温度为25 ℃，水力直径DH=4S/L，L 为入口周长，S 为入口截面积，湍流尺度l=0.07DH。风来流为速度入口，燃气射流为质量入口，出口为x 轴正向，设为压力出口，地面及发射筒表面设为无速度滑移、无质量渗透壁面，剩余三个面设为对称面。计算时先用稳态定常算法，得到收敛后的数据作为初场，再开始非定常的流场计算，时间步长为0.1 s。当氯气最大体积分数低于30×10-6时，停止计算。

3 数值模拟结果与分析

3.1 风速影响分析

山顶发射，风速0 m/s 时，氯气污染物不同时刻的扩散情况如图4 所示。可以看出，t=1 s 时，燃气从筒中喷出，此时氯气扩散距离较小。随着时间推移，氯气影响范围逐渐扩大，到t=50 s 时，氯气的扩散距离几乎达到最大值（x=36.6 m）。随后氯气的影响范围逐渐减小，浓度迅速降低。到t=139 s 时，氯气基本消散，体积分数小于30×10-6。

风速为10 m/s 时，氯气污染物不同时刻的扩散情况如图5 所示。由图5 可以看出，氯气团的运动速度明显更快。t=1 s 时。扩散距离已经达到x+=22.7 m；到 t=6 s 时，氯气团覆盖范围基本达到最大，|x|=107.3m；t=18s 时，氯气大部分已消散，此时扩散距离为x=219.9 m。

对比山顶发射时不同风速下的氯气扩散情况。如图6 所示，可以看到，风速越大，氯气的扩散速度越快。风速小于10 m/s 时，扩散距离随着风速增大呈减小趋势；风速大于10 m/s 时，风速越大，扩散距离越远。风速为2 m/s 时，扩散时间最长（t=139 s）；风速为18 m/s 时，扩散距离最远，xmax=249 m。从图7 中可以看出，风速越大，任意时刻氯气的覆盖范围越广，影响的时间越短。风速为2 m/s 时，氯气团的影响时间最长。由以上分析可知：风速越大，氯气扩散速度越快，影响时间越短；风速越小，氯气扩散得越慢，影响时间越长。

图4 风速为0 m/s 时不同时刻氯气浓度2D 云图

图5 风速为10 m/s 时不同时刻氯气浓度2D 云图

图6 不同风速氯气扩散情况

3.2 山地影响分析

为考察起伏地形对氯气扩散的影响，将发射阵地移至山底，计算2、5、10、15 m/s 共四种风速下氯气的扩散情况，对比山顶发射与山底发射时氯气的扩散距离、扩散浓度，分析山地对氯气扩散运动的影响。

不同风速时，氯气扩散距离随时间的变化曲线如图8 所示。可以看出，山顶发射时，氯气扩散的距离更远，运动速度更快；山底发射时，氯气的扩散运动受到山地影响，扩散距离短，运动速度慢，而且越靠近山地坡度大的位置，氯气扩散运动越缓慢。风速为15 m/s 时，山底发射氯气扩散的最远距离为221 m。由图8 还可以看出，无论在何种风速下，t0后任意相同时刻，山顶发射的氯气团扩散距离都比山底发射要远，这说明起伏的山地能够减小氯气扩散距离与扩散速度。

风速为5m/s 时，x=50 m、x=100 m 和x=200 m处氯气浓度随时间的变化曲线如图9 所示。观察氯气浓度变化可以看出：初始阶段山顶发射氯气浓度高于山底发射，但是随着时间推移，山底发射的氯气浓度逐渐高过山顶发射。这是由于气流在迎风面上坡处堆积，速度梯度与浓度均增大；在山底背风面下坡处，由于气流的回流作用，氯气浓度也比较大。以上分析说明，山地地形迎风面上坡处与背风面下坡处，氯气浓度均较大，是危险区域。

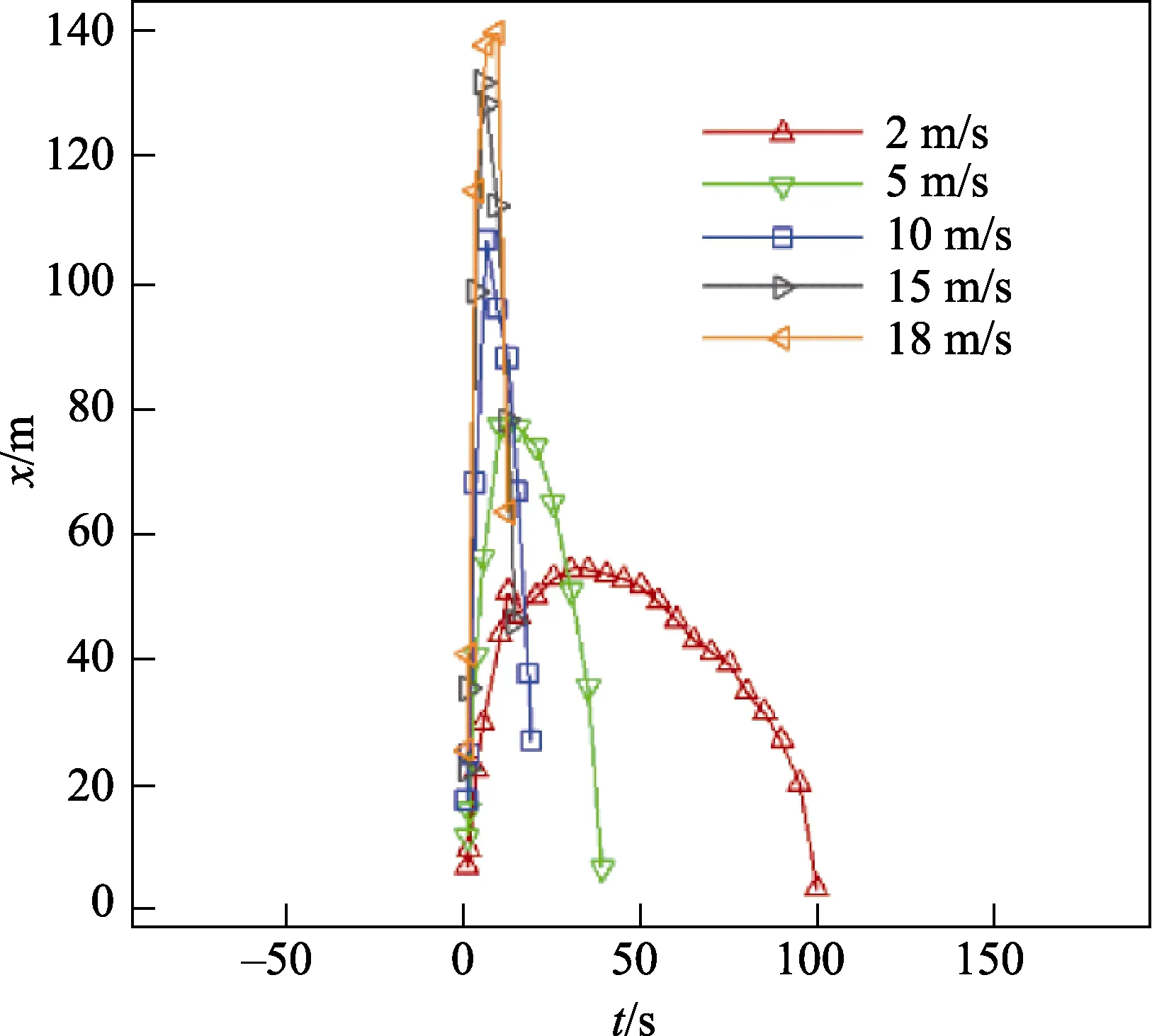
图7 不同风速氯气覆盖情况

图8 不同发射点氯气扩散情况

图9 氯气浓度变化情况

4 结论

文中采用CFD 方法及FLUENT 软件，以氯气为标的物，对燃气发生器产生的有毒气体在不同风速、山地影响下的扩散过程进行了数值模拟，并进行了安全性分析。通过以上分析可知，不同风速和起伏山地对氯气的扩散会产生重要影响。

1）山顶发射时，风速越大，氯气的扩散速度越快，风速为18 m/s 时，扩散距离最远，xmax=249 m。

2）山底发射时，在相同风速下，氯气的扩散距离、扩散速度均小于山顶发射。风速为15 m/s 时，扩散距离最远，xmax=221 m。

3）山地对氯气扩散的影响主要是减缓氯气团的运动速度，减小氯气污染物的影响距离。在山地迎风面上坡与背风面下坡，由于气流的积聚与回流作用，氯气浓度降低较慢，影响时间更长。

4）在制定安全距离策略时，应当根据发射位置、风速风向和山地起伏划出合理的安全距离。文中计算结果受计算地形所限，不能包括所有情况，但理论与方法是合理的，在划定安全距离时可以将文中的最大扩散距离作为参考。