电润湿显示系统的电光响应机理及特性
2019-08-20林珊玲林志贤郭太良钱明勇曾素云
林珊玲,林志贤*,郭太良,钱明勇,曾素云,唐 彪
(1.福州大学 平板显示技术国家地方联合工程实验室,福建 福州 350116;2.福州大学 物理与信息工程学院,福建 福州 350116;3.华南师范大学 广东省光信息材料与技术重点实验室,广东 广州 510006)
1 引言
电润湿显示(Electrowetting display,EWD)技术自提出以来[1-2],因其低功耗、响应速度快、反射率高、相对电泳电子纸显示器可实现动态视频显示等优点,而得到了广泛的研究。从实验上对电润湿显示器件的研究主要包括制作工艺、器件材料、像素结构等对显示性能的影响方面,而为了节省材料、成本等提出一系列以流体运动机制机理为基础的仿真模型[3-6],通过仿真模型改变材料的参数、像素结构等来研究对显示性能的影响。
Ku等[7]首先尝试电润湿显示系统中微流体运动的建模和模拟。他们采用ANSYS FLUENT仿真软件,提出了基于流体连续体表面力(VOF-CSF)体积的3D模型来描述在不同电极情况下像素内部的动态流体行为。但模型中忽略了由电润湿效应引起的接触角的变化,这降低了模型的适用性。Hsieh等[8]尝试利用3D模型来精确预测电光转换过程中的流体动力学。通过将由麦克斯韦应力张量推导出的电流体动力学(Electrohydro dynamic,EHD)力与油水双相的层流相场耦合,成功地模拟了电流体显示(Electrofluidic displays,EFD)开关过程的流体运动及其相应的电光性能。但是油膜破裂模式以及油膜破裂后油膜的运动方向、油膜破裂的时间以及油膜恢复的时间与实验观测不符。基于VOF(Volume fraction equation)方法,Roghair等[9]采用OpenFOAM框架,提供实现电润湿显示系统建模的工具。他们通过将高斯定律和电荷输运方程结合到流体流动的Navier-Stokes方程中来求解电流体动力学方程,成功模拟了在外加电场作用下流体-流体界面的变化,从而很好地描述了像素中的流体运动。但是在仿真过程中介电质的电场常数没有梯度耦合,引起了电势分布误差,而涉及的数值求解过程较为复杂,使得该方法的应用受到极大的限制。Tang等[10]提出了一个电毛细管波模型,通过薄膜润滑理论建立了封闭系统下的电润湿器件的油膜破裂模式理论,更全面地了解受EHD系统像素壁限制的水/油界面的行为。这项工作得到了关于在受限的电-毛细管流体系统中存在离散化模式的理论描述,描述了像素开关期间的电压依赖性油膜破裂过程并且提供了与之相符的经验证据。Clime等[11]通过三维Lattice-Boltzmannn模型成功实现了对电润湿数字微流控器件的传输、合并、分裂等基本操作的仿真,并与实验结果相吻合。然而在非开放式电润湿系统中,像素墙对油膜的运动具有约束作用,Lattice-Boltzmannn模型无法体现亚毫米结构下由像素墙引起的毛细效应。庄磊等[12]提出在COMSOL架构下,通过耦合层流两相流相场与静电场的方法,模拟非开放式电润湿器件的油膜破裂过程,并探究导电液体的动力黏度以及油水表面张力对油膜破裂的时间、开口率的影响。Zhou等[13]基于总体能量守恒(Overall energy balance,OEB),对EHD的开关特性进行分段描述。“开”过程包含初始状态、快速响应的去润湿过程以及油滴的慢速重组过程;“关”过程包含快速响应的润湿过程以及油水界面重新恢复到初始阶段的过程。该模型仿真结果与实验数据相符,且很好地描述了电润湿在开和关过程中光学响应的迟滞现象[14-15]以及油膜破裂和重组的时间。
近年来主要采用耦合电场与Navier-Stokes流体方程的方法,研究电润湿显示器的流体运动及其电光响应并取得了较好的效果,为理解影响EWD的动力学现象的物理学方面做出了重大的贡献。本文采用OEB方程及电场作用下的杨氏-拉普拉斯(Young-Laplace)[16-18]方程联立的方法,建立了合成表面物理和流体力学理论并包含最小经验理论的电润湿显示系统理论模型,模拟电润湿显示器电光响应过程及电流体运动特性,并探究油水表面张力对电光响应过程的影响。实验结果表明,开启电压越大响应时间越快,油水表面张力越大时电润湿显示器响应越慢,像素电光响应时间量级的模拟结果与相同参考几何的实验数据具有良好的一致性。
2 电润湿显示器件工作原理及仿真机理
2.1 电润湿显示器件工作原理
电润湿显示像素结构及其驱动原理如图1所示。电润湿显示像素结构包括反射层、疏水绝缘层、彩色油墨层、水层、亲水像素墙以及上基板。当像素没有施加电压时,油墨平铺在疏水绝缘层上,此时像素处于关状态,如图1(a)所示。当像素施加电压时,油墨收缩,光线透过疏水绝缘层经反射层反射回来,此时像素处于开状态,如图1(b)所示。油墨收缩的不同程度代表着不同的光学状态,而油墨收缩的程度由电压大小决定,且当驱动电压小于阈值电压时,油墨不收缩。开口率[19-20]表征电润湿显示像素的开关情况,其计算公式如下:
(1)
其中,πR2为油墨收缩后与疏水绝缘层的接触面积,L为像素的一半边长。
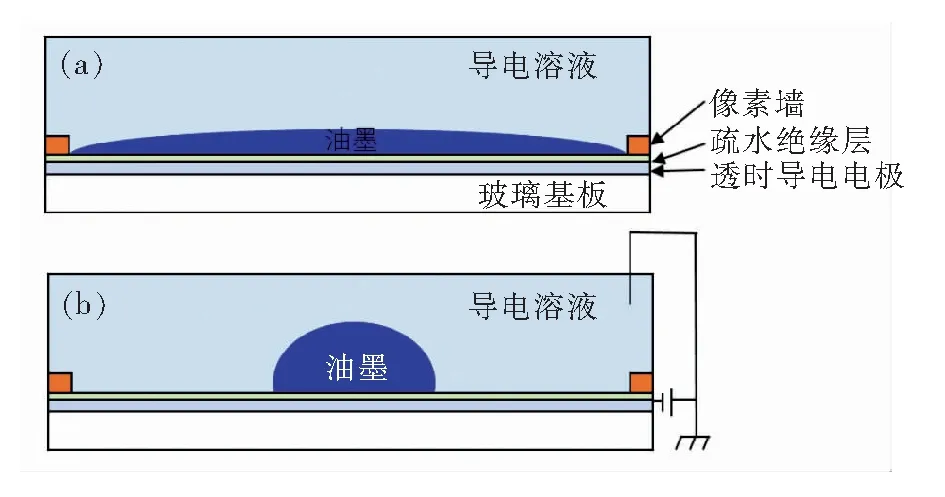
图1 电润湿显示原理。(a)未加电压情况下,油墨铺展在绝缘介质层上;(b)加电压情况下,油墨收缩。Fig.1 Electrowetting display principle.(a)Without applied voltage,oil spreads over the hydrophobic insulator.(b)DC-voltage applied,the oil film is contracted.
仿真系统通过Young-Laplace方程追踪油水界面的变化,得到的三相接触角、油水接触面积、油相固相接触半径等参数用于总体能量守恒方程,以求解电润湿的电光响应过程。
2.2 总体能量守恒方程
电润湿显示像素开关过程中,系统满足总体能量守恒方程。电润湿显示系统能量守恒方程如公式(2)所示:
(2)
其中,Ee为外加电场的场能,Ep为界面势能,Ek为分子势能,Eg为重力势能,wv为黏性耗散能。
为将总体能量守恒方程进行化简,我们通过计算电润湿显示像素系统中Bond数Bo以及雷诺数Re实现。Bond数Bo表征重力和表面张力的关系,雷诺数Re表征粘滞力和惯性力的关系:
Bo=Δρgh2/row,
(3)
Re=Δρgh2/μ,
(4)
其中,Δρ为油水的密度差,g为重力加速度,在电润湿显示像素系统中,Bo=1.4×10-6≪1,因此重力可以忽略;Re=0.05,当Re<2 000时,为层流状态,此时惯性力可以忽略。因而,在电润湿显示像素系统中,只需考虑电场力、黏性耗散以及界面张力。
总界面势能包含油-水界面势能、油-疏水绝缘层界面势能、水-疏水绝缘层界面势能,表达式如公式(5)所示:
Ep(t)=Eow(t)+EoAF(t)+EwAF(t)=
rowAow(t)+roAFAoAF(t)+rwAFAwAF(t),
(5)
其中,E(t)、r、A(t)分别表示界面势能、界面张力、接触面积;下标o、w、AF分别表示油墨、水以及疏水绝缘层。
根据Young-Lippman方程
rwAF=roAF+rowcosθe,
(6)
且疏水绝缘层与水的接触面积以及疏水绝缘层与油的接触面积始终为像素面积的大小:
AoAF(t)+AwAF(t)=Apixel,
(7)
于是公式(5)可以化简为
Ep(t)=row(Aow(t)-AoAF(t)cosθe)+rwAFApixel,
(8)
其中
(9)
AoAF(t)=πR2(t).
(10)
根据润湿理论近似(Lubrication theory approximation)即认为电润湿系统中三相接触线是存在滑移的边界条件,则三相接触线上单位长度的黏性耗散力可由公式(11)[21]表示:
(11)
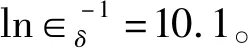

(12)
施加于电润湿显示系统的电场力为
(13)
其中,ε0为真空介电常数,V为施加的电压。
则电场能为
(14)
对于电润湿显示像素系统,从t=0时刻到任意时刻t,满足总体能量守恒方程
Ep(t)-Ep(0)+wv(t)-wv(0)=
Ee(t)-Ee(0),
(15)

2.3 Young-Laplace方程
Young-Laplace方程是表示液面曲率与液体压力之间关系的公式:
(16)
其中,ΔP、P0、Pw分别是油-水界面的压差、油相一侧的压力、水相一侧的压力,R1和R2是界面的曲率半径。
在电场作用力下的电润湿显示驱动系统,油水界面的Young-Laplace方程可由下式表示:
(17)
其中,En表示电场的法向分量,y(x)表示界面形状的函数。由于油膜始终保持为球冠形,油相和水相两侧的参考压差ΔP0可以由拉普拉斯方程在油膜顶点处的值表示,即
(18)
其中,R0(t)为油-水界面顶点处的局部曲率半径。
对于y=y(x)曲线,曲径半径R1和R2可表示为:
(19)
(20)
则
(21)
公式(21)为二阶微分方程,其边界条件为公式(22)、(23):
y(x=0)=H(t),
(22)
(23)
3 仿真过程及实验测试平台
仿真过程中,系统中水的密度ρw=998 kg·m-3,油墨密度ρ0=735 kg·m-3,油墨黏度μ=0.001 2 Pa·s,油水界面张力row=0.022 N·m-1,相对介电常数εd=1.934,像素大小Apixel为150 μm×150 μm,注入的油墨体积V0=5×10-14m3,像素墙高度h=5.5 μm,疏水绝缘层厚度dAF=0.85 μm。如图2所示,假定油墨在收缩和铺展过程中始终保持球冠形,图中θd(t)接触角,H(t)为油滴中心的高度,R(t)为油墨与疏水绝缘层接触面的半径。
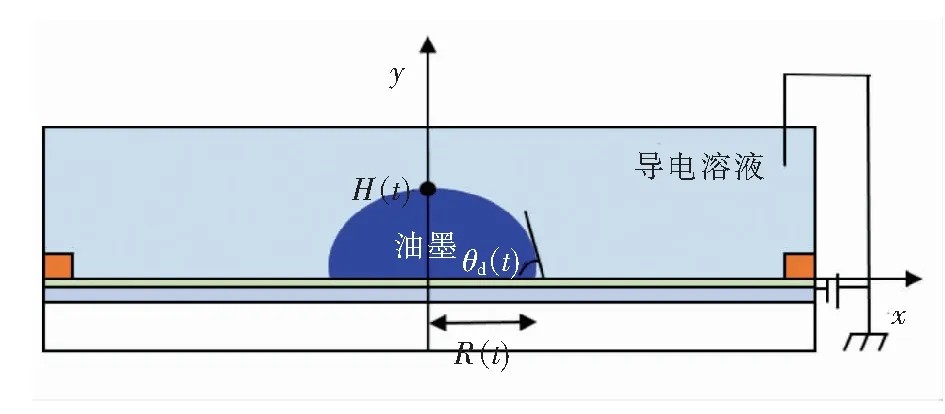
图2 仿真模型示意图Fig.2 Schematic diagram of modeling
3.1 油-水界面形状的求解
油-水界面形状即Young-Laplace求解可分为以下几个步骤:
(2)通过变量替换法将二阶微分方程化成两个一阶微分方程。
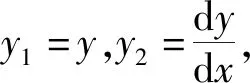
二阶微分边界条件对应为两个一阶微分方程的初始条件为y1(x=0)=H(t),y2(x=0)=0。

(4)利用四阶龙格库塔方法求得y=y(x)及其一阶导数的数值解。
(5)油墨体积在系统中视为恒定值,将其作为约束条件。将H(t)和求得的y(x)代入约束条件中,重复(2)~(4)步骤使求得的体积在油墨体积期望精度范围内:

(24)
(6)根据求得的y(x),可得到相应的R(t)和θd(t):
y[x=R(t))]=0,
(25)
(7)判断求得的y(x)、R(t)和θd(t)与开始假定的油-水界面的形状是否一致,若不一致,重复(1)~(6)步骤,直到y(x)、R(t)和θd(t)与开始假定的油-水界面的形状一致。
3.2 电润湿显示像素电光响应关系求解
电润湿显示像素在电场作用下,电光响应关系亦即开口率随时间变化过程模型求解步骤如下:
(1)在t=0时刻,各参数初始值R(0)=L/2,通过体积约束条件及油水界面Young-Laplace方程可得到R0(0)。
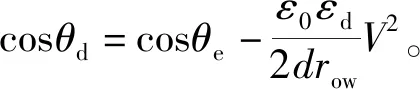
(3)将上述计算出的值代入OEB方程,得到Δt。
(4)改变ΔR0的值,重复步骤(2)、(3),以进一步提高模型的准确性和有效性。
(5)改变电压值,重复步骤(2)、(3)、(4),得到不同电压作用下,电润湿显示像素开口率WA与时间t的关系曲线。
3.3 实验测试平台
为测量电润湿显示像素的实际开口率与电压的关系,搭建如图3所示的测试平台。信号发生器用于产生驱动电压,高速摄像机用于拍摄电润湿器件油墨收缩铺展的情况,色度仪记录电润湿显示器件的反射率,计算机用于处理高速摄像机拍摄下来的图像并将色度仪记录的反射率换算成电润湿显示器件的开口率。
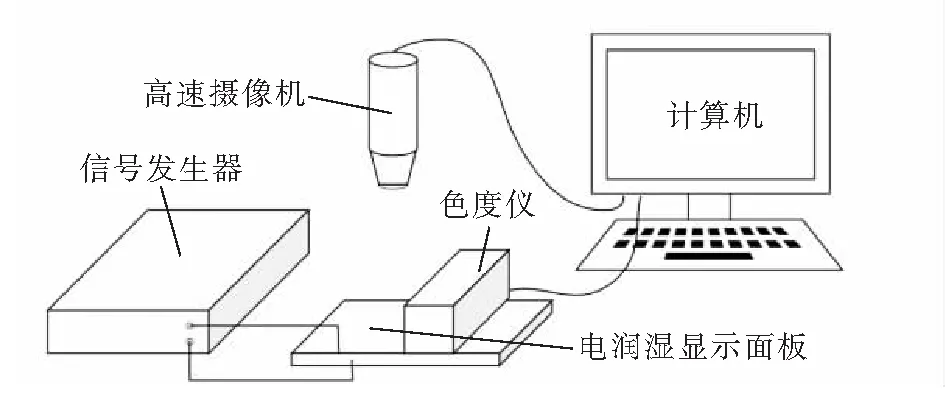
图3 电润湿显示器件开口率和响应时间的测试平台Fig.3 Test platform of white area and response time of electrowetting display
4 结果与讨论
EWD像素的光学响应从油膜的破裂开始,而不是施加电压的时间。油膜破裂的开始时间导致光学响应的延迟,而延迟时间依赖于施加电压的大小,施加电压越大,延迟时间越小。在图4(a)中,将延迟时间的估计值与实验值进行比较。仿真结果中40 V电压情况下,油墨的延迟时间为0.37 ms,与Zhou[13]所建模型的延迟时间0.33 ms以及Hiseh等[8]的延迟时间0.4 ms一致。仿真结果与实验结果虽量级一致,但与实验结果相比延迟时间较小。这种差距的主要原因在于以下几点:仿真过程中的模型假定油墨与水的界面形状始终保持为球冠形,而实际电润湿中油墨的运动不会一直保持规则的形状,且油墨会出现分裂等现象,当油墨的形状发生改变时,将会影响电场的重新分布,因而影响其响应延迟时间;实际油墨的运动除了收缩之外,还有油墨重心的偏移,即油墨会运动到像素的某个角落或某几个角落,此时动摩擦力会增大从而影响电润湿像素的响应时间。
实验结果中,在25,30,35,40 V电压下,电润湿的响应时间分别为32,24,16,9 ms,且在最后的开口率无法达到满足Young-Lipmann条件下的理想开口率。因油墨在电压驱动下会出现如油墨分裂、电荷俘获等现象,直接导致电润湿显示器的开口率下降的问题[22]。油墨分裂、电荷俘获现象机理仍是电润湿显示器待研究的问题,仿真模型中未进一步考虑,因而得到的结果较为理想。

图4 (a)油膜破裂延迟时间;(b)像素开口率随时间变化趋势。Fig.4 (a)Film rupture time.(b)Pixel aperture ratio changes with time.
经Young-Lipmann计算的在不同界面张力下三相接触角的大小如表1所示,界面张力越大时,三相接触角越小,从而导致电润湿的开口率减小。在模型中,计算了30 V电压下界面张力从0.022 N/m增加到0.040 N/m的电润湿响应时间,如图5所示。随着界面张力的增大,响应时间增大,即油墨的运动速度变慢,电润湿的光电响应变慢。
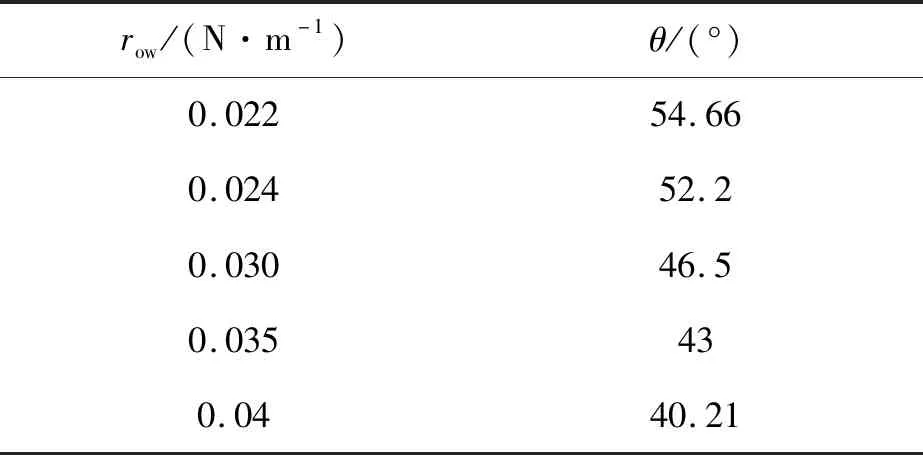
表1 30 V电压下不同油-水界面张力对应的接触角Tab.1 Different oil/water interfacial tension and the equilibrium contact angle resulting from V=30 V
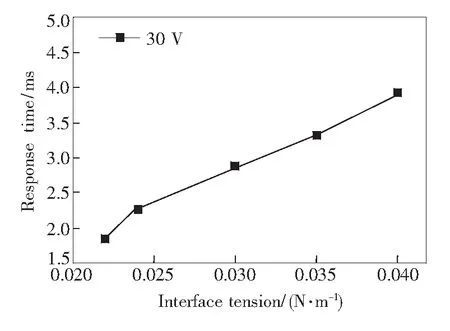
图5 30 V电压下不同油-水界面张力对应的响应时间Fig.5 Different oil/water interfacial tension and the optical response time resulting from V=30 V
5 结论
通过Young-Laplace计算电润湿显示像素在电场作用下油水界面的变化,结合OEB方程计算电润湿显示像素的延迟时间及其开口率与时间的变化趋势。模型在25,30,35,40 V电压下延迟时间分别为3.4,1.9,1,0.37 ms,与实验测量的数据4.8,2.5,2,1 ms在同一量级,且随着电压增大响应时间减小的趋势一致。并且在模型的基础上研究了界面张力对电润湿显示像素的影响,界面张力的增加导致电润湿的响应时间增大,像素开口率减小,油墨运动速度变慢。因此实际器件设计中,应选择较小数值的界面张力。
致谢:感谢华南师范大学提供的电润湿电子纸显示屏以及测试环境。
