风电叶片拉挤碳纤维梁与蒙皮富胶强度研究*

文 | 冯学斌，白会超，张文伟，邓航，高康

目前风电叶片的制造普遍采用全尺寸的真空灌注成型工艺，并以灌注玻璃纤维为主流。但是随着功率需求的增加，叶片设计越来越长，且由于整机重量、轮毂尺寸以及叶片生产和运输等因素限制，叶根圆环半径无法与长度成比例增加，叶片在弦向和厚度尺寸也无法成比例增加。若仍采用相同材料，随着叶片长度设计越来越长，叶片柔性越来越大，材料强度冗余、刚度不足的现象将进一步严重。相较于玻璃纤维，碳纤维刚度和强度均有较大的提升，尤其刚度，碳纤维模量可达到玻璃纤维的3倍以上，其比强度和比模量大大优于玻璃纤维。在叶片尺寸达到一定极限后，碳纤维相较于玻璃纤维优势会越来越明显，风电行业内80m级以上叶片出现多款碳纤维叶片设计，LM设计的107m超长碳纤维叶片，也刷新了人们对叶片材料设计的认识。

在材料应用上相较于灌注碳纤维布形式，拉挤型碳纤维板材工艺更稳定，其纤维含量进一步提升，板材模量进一步增加，能更好地克服长叶片刚度不足、强度冗余问题。拉挤型碳纤维板材在拉挤预应力下，能更好克服碳纤维原丝蜷曲带来碳纤维灌注板材性能不稳定问题。但是由于应用上的不成熟，目前拉挤型碳纤维板材只能做成平面直条形状。平面直条形状与叶片外形曲面弧形必然产生缝隙，在与叶片其余部件一起灌注成型时，拉挤碳纤维梁与蒙皮会产生富胶缺陷，造成碳纤维梁强度冗余、富胶缺陷先破坏的情况，降低结构整体可靠性。

本文针对这一情况，灌注含（2、4、6、8、10）mm厚富胶碳纤维梁-蒙皮试样，在标准MTS机上利用四点弯曲方法，研究不同富胶厚度下试样的强度，并建立有限元分析模型，计算测试载荷下试样碳板、蒙皮及富胶的应变。测试及有限元分析结果可作为拉挤型碳纤维梁叶片设计参考。

测试试样及方法

一、测试试样

试样材料选择拉挤碳纤维板、双轴布、三轴布、树脂。考虑蒙皮较薄，在四点弯曲试验中，加载压头压在碳板侧，支撑点位于蒙皮富胶侧，支撑位置用玻纤布填充。

试样长1000mm，宽200mm，拉挤碳板厚10mm，富胶厚2～10mm，蒙皮厚约1.5mm，总厚度约21.5mm。试样尺寸、实物及富胶厚度如图1-图3所示。

二、测试方法

拉挤碳板与蒙皮富胶试样强度测试，采用四点弯曲加载测试方法。其中主要实验参数参考ASTM C 393 四点弯曲测试标准，具体加载位置和支撑位置以及应变片位置如图4所示，试样加载实物图如图5所示。样件碳板侧为上表面，富胶蒙皮侧为下表面，加载（F）的压头压在上表面碳板侧，支撑位置位于下表面垫布加强区域。

图1 测试试样几何尺寸

测试结果及分析

根据上述测试方法，加载试样直至样件达到极限强度破坏。根据对不同富胶样件破坏形式进行统计，对于富胶厚度2～8mm试样，碳板侧先发生破坏，富胶侧无明显破坏迹象，如图6中a、b、c所示。对于富胶厚度为10mm样件，富胶侧先破坏，富胶区域出现多条贯穿性裂纹，碳板侧无明显破坏迹象，如图7中a、b、c所示。

测试不同富胶厚度样件上下表面应变，结果如图8至图12所示。

图2 测试试样实物图

图3 测试试样富胶厚度实物图

图4 试样加载示意图

由各个样件应变测试结果可知，不同富胶厚度样件破坏时，上下表面最大应变如表1所示。

由表1可知，对于富胶厚度2～8mm试样，试样破坏时，碳板侧拉伸应变在8000微应变左右，碳板侧先发生破坏，破坏形式为分层和断裂；富胶侧拉伸应变在10000微应变以内，未发生明显破坏迹象。对于富胶厚度10mm样件，富胶侧拉伸应变达到10429微应变，富胶侧先发生破坏，碳板侧未发生明显的破坏。随着富胶厚度的增加，富胶侧拉伸应变逐渐增大，厚度达到10mm时碳板侧应变明显下降。由于实验中只能监测试样上、下表面长度方向（11方向）应变，无法测试厚度方向的应变，不同厚度富胶对试样层间性能的影响需要建立有限元模型作进一步研究。

图5 试样加载实物图

图6 富胶厚2至8mm试样破坏形式

仿真分析

一、仿真模型

利用abaqus软件建立试样的三维有限元模型，如图13所示。富胶区域、拉挤碳板、蒙皮以及支撑垫布区域均采用实体单元C3D8R，富胶区域采用各向同性材料，其余区域采用三维各向异性材料等效工程常数模拟。坐标系1方向为试样长度方向，2方向为试样宽度方向，3方向为试样厚度方向。分别建立（2、4、6、8和10）mm厚胶层有限元模型，在实验载荷与支撑条件下，计算试样上下表面1方向拉、压应变以及胶层、碳板3方向拉、压应变与胶层、碳板1、3方向的剪切应变。

图7 富胶厚10mm试样破坏形式

图8 富胶厚2mm试样上下表面应变

二、仿真结果分析

在实验载荷和约束条件下，当试样破坏时，计算出不同富胶厚度试样上下表面的最大拉、压应变，胶层、碳板的层间最大剪切应变、拉伸应变，如表1所示。

图9 富胶厚4mm试样上下表面应变

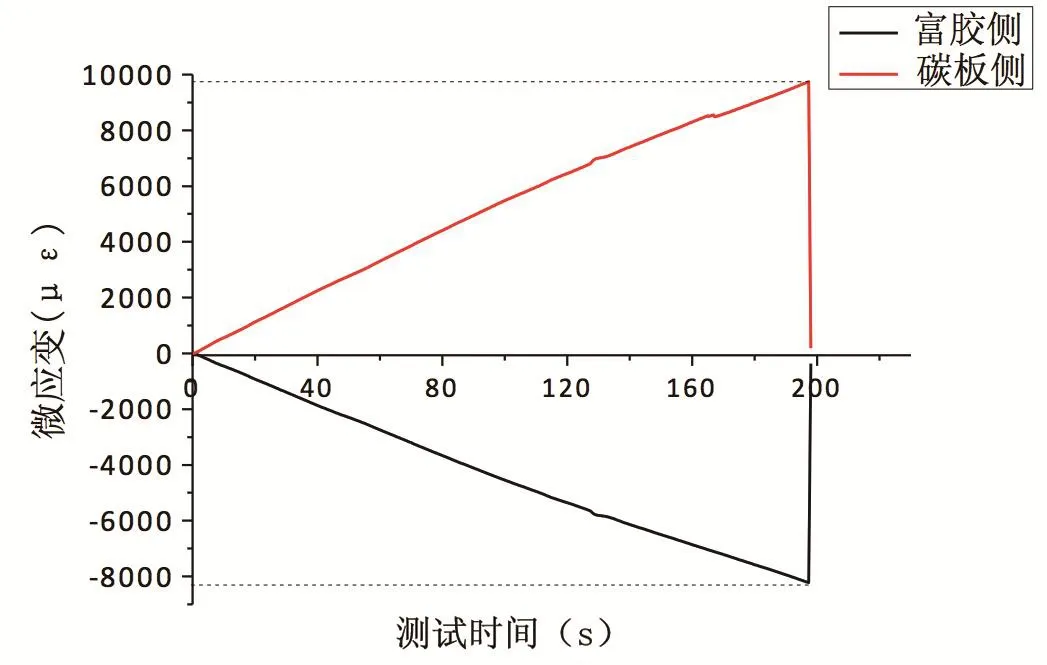
图10 富胶厚6mm试样上下表面应变

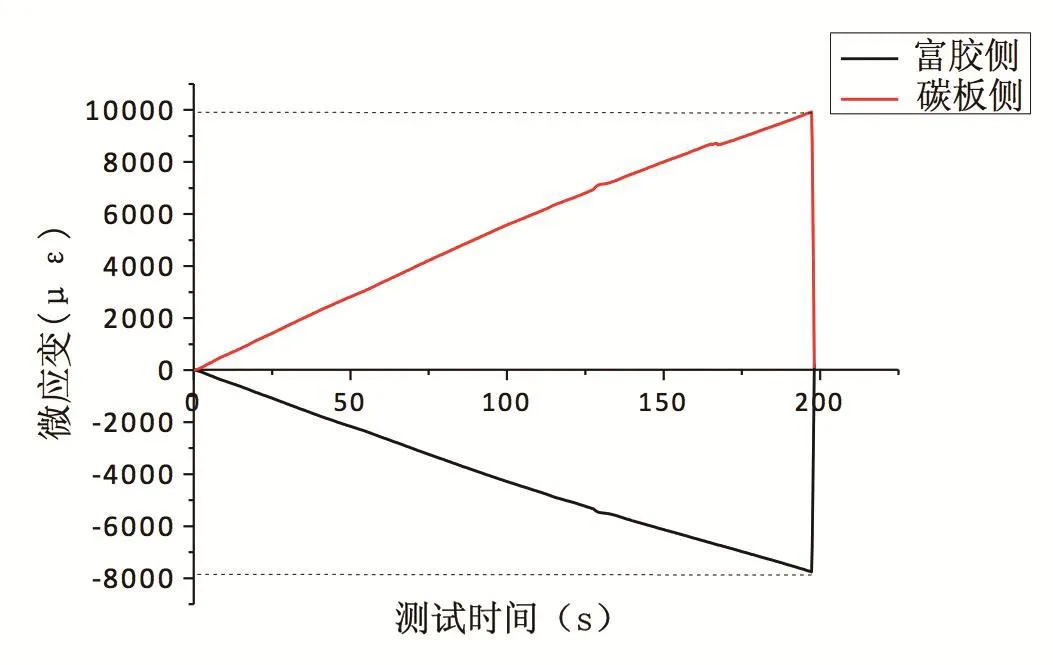
图11 富胶厚8mm试样上下表面应变

图12 富胶厚10mm试样上下表面应变

图13 富胶试样有限元模型

表1 不同富胶厚度样件计算应变（με）统计表

由表1可知，在测试载荷下，样件破坏时，有限元计算富胶侧与碳板侧拉伸、压缩应变与测试值水平基本一致，相对误差在5%以内。随着富胶厚度增加，碳板与富胶的厚度方向拉、压应变，以及弯曲引起的1、3方向剪切应变相应增加，表明富胶厚度增加引起试样层间性能下降，富胶区域尤其明显。验证了上文中当富胶厚度增加至10mm，富胶侧拉伸应变未达到富胶本身断裂应变、富胶侧即发生破坏的结果。可推测当富胶厚度增加到一定程度，富胶区域出现的贯穿性裂纹是由拉伸与层间剪切综合作用导致的。

结论

在风电叶片复合材料应用时，富胶被视为一种缺陷，尤其在应用拉挤碳纤维梁时，由于拉挤碳纤维板的平面直条特性与叶片外形曲面弧形特性的差异，不可避免带来较多的富胶区域。本文研究了不同富胶厚度对试样拉伸、压缩及层间强度的影响，但不同于本文试样中富胶的规则形状，风电叶片实际应用中，拉挤碳纤维梁与蒙皮富胶形状较为复杂，尤其不同厚度和形状的富胶对试样的疲劳性能还需要进一步研究。

从测试及有限元分析结果可得出规律和结论：（1）对于富胶厚度2～8mm试样，碳板侧先发生破坏，破坏形式为碳板分层和断裂，富胶侧未发生明显破坏迹象；（2）对于富胶厚度10mm试样，富胶侧先发生破坏，沿试样宽度方向，富胶区域发生多条贯穿性裂纹，碳板侧未发生明显破坏迹象；（3）有限元计算富胶侧与碳板侧拉伸、压缩应变与测试值水平基本一致，相对误差在5%以内；（4）随着富胶厚度增加，测试和有限元计算结果表明，富胶侧拉伸应变均增加；（5）随着富胶厚度增加，有限元计算结果表明，富胶和碳板区域厚度方向应变，以及弯曲变形带来的剪切应变均明显增加，可推测由于富胶增加导致试样层间性能降低。