大跨度铁路下承式钢桁梁柔性拱桥稳定性研究

施 洲，张 勇，张育智，夏正春

(1.西南交通大学 土木工程学院，四川 成都 610031；2.中铁第四勘察设计院集团有限公司 桥梁设计研究院，湖北 武汉 430063)

近十年来我国大跨度铁路桥梁建设发展迅猛，涌现了一批造型优美、结构复杂的大跨度钢桁梁柔性拱桥，其中包括主跨229.5 m的合福铁路合肥南环线双线铁路桥，双主跨220 m的厦深铁路榕江双线铁路桥，主跨336 m的沪通长江大桥天生港专用航道公铁两用桥以及正在建设中的主跨为2×360 m的南沙港铁路洪奇沥水道特大桥。南沙港铁路洪奇沥水道特大桥是国内最大跨度的双线铁路钢桁梁柔性拱桥。钢桁梁柔性拱桥通过拱结构及吊杆为连续钢桁梁提供多点弹性支撑，显著增强钢桁梁的跨越与承载能力，但该桥型结构中拱肋及部分桁梁杆件以受压为主，其稳定问题非常突出。

国内外由于桥梁失稳造成的灾难时有发生，长久以来已有大量研究者开展了钢桥的稳定性研究工作[1-6]，早期，拱桥等结构的稳定分析主要采用理想状态下的线弹性方法，但客观存在的构件制作、安装初始偏差，这将导致钢桁梁拱桥发生极值点失稳破坏，且研究表明[4,6-8]采用线弹性方法计算的结构稳定安全系数比考虑非线性的稳定系数大，过高估计了结构的实际稳定承载能力。1948年Chatterjee[1]首次将结构几何非线性运用到计算拱桥结构极限承载力分析中，并建立了拱桥第2类稳定分析的挠度理论；1977年Sadao等第1次在有限元中考虑结构的几何非线性分析拱桥的第2类稳定问题；郑凯锋等通过对钢拱桥的稳定分析，提出了综合初始横向缺陷、横向位移和拱圈横向整体刚度3因素的结构稳定验算方法；程进等以上海卢浦大桥为研究对象，进行了钢拱桥稳定计算方法的研究，并探究不同荷载分布方式对结构稳定性的影响；谢旭等经过对大跨度两铰钢拱桥的稳定分析，发现荷载加载顺序对结构承载能力影响很小；王璇等只针对2种不同加载情况下的钢桁架柔性拱桥的稳定性进行了分析。虽然钢桁架柔性拱稳定方面的研究工作由来已久并取得众多成果，但随着跨径的不断加大，其在铁路荷载下稳定问题将更加显著，而关于大跨度铁路钢桁梁柔性拱桥的非线性稳定性问题的研究仍然较少。本文基于洪奇沥水道特大桥主跨为2×360 m的大跨度铁路钢桁梁柔性拱桥建立有限元模型，系统分析其在施工至运营阶段多工况下的稳定性能，研究几何非线性、材料非线形、桥梁整体及杆件初始几何位移等因素对钢桁梁柔性拱桥稳定性能的影响，以及大跨度钢桁梁柔性拱桥的失稳路径和实际稳定性。

1 钢桁梁拱桥稳定性理论及分析方法

不考虑结构初始缺陷及几何非线性的稳定问题可转化为求解结构方程特征值的问题[9]，即第1类稳定，是实际稳定承载力的上限。对于实际桥梁结构，考虑材料非线性和几何非线性对稳定承载力的影响更符合实际情况，即第2类稳定问题，其基本方程为

(Ke+Kg+Kl)φ=F

(1)

式中：Ke为桥梁有限元模型的弹性刚度矩阵；Kg为几何刚度矩阵；Kl为大位移刚度矩阵；φ为结构失稳模态向量；F为外加荷载向量。

对于非线性稳定求解问题，式(1)中刚度矩阵随荷载的改变而变化，因此非线性增量平衡方程求解更为复杂。已有研究表明[10-12]，增量迭代法用于桥梁结构稳定分析具有较高的精度和较快的计算速度，它首先将桥梁的极限荷载Fcr划分为n份荷载增量ΔFi(i=1,2,…,n)，然后依次增加少量荷载ΔF。每次荷载增量ΔF叠加后，假定加载过程中结构的刚度不发生变化。将增量迭代过程中的所有轴力因素和荷载—位移关系计入，可将复杂的非线性问题用多次线性迭代的结果来逼近，相应增量平衡方程为

Ki-1Δφi=ΔFi

(2)

其中，

Ki-1=Ke，i-1+Kg，i-1

式中：Ki-1为荷载进行完第i-1次叠加后的刚度矩阵。

2 大跨度铁路下承式钢桁梁柔性拱桥计算模型

2.1 工程概况

南沙港铁路洪奇沥水道特大桥主桥是设计速度为120 km·h-1的双线中—活载铁路下承式钢桁梁柔性拱桥，跨径布置为(138+2×360+138) m，其中钢桁梁由2片高为16 m的华伦式主桁组成，桁间距15 m，桥梁宽15 m，主跨的宽跨比1/24。拱结构采用钢箱拱肋，以上弦杆为基准线拱肋矢高为65.0 m，矢跨比1/4.67，主桥结构形式如图1所示。桥面布置中，在钢桁梁两侧下弦杆节点处设置横梁，横梁上共设间距2 m的4根纵梁形成明桥面结构。为避免纵梁在纵向传力，纵梁沿纵向每2个节间断开并设置纵向活动铰。全桥共设有84根吊杆，吊杆上端锚固于拱肋节点，为非张拉端，下端锚固于上弦节点，为张拉端。上下锚固节点处设钢锚箱，钢锚箱与节点板焊成整体。桥梁的主结构采用Q370qE钢材，联结系采用Q345qE钢材，吊杆采用抗拉极限强度为1 770 MPa的高强平行钢丝。

图1 全桥立面布置图(单位：mm)

2.2 有限元模型

为了实现对大跨度钢桁梁柔性拱桥稳定问题的精确分析，采用通用有限元软件ANSYS对洪奇沥水道特大桥进行建模。其中桥梁的拱肋、钢桁梁以及拱肋的横向连接杆件等均采用梁单元BEAM188模拟，吊杆采用3DLINK8单元模拟，有限元模型如图2所示。划分单元时将每个吊杆间的拱肋细划分成5个梁单元，采用多折线模拟拱肋曲线形状。有限元模型中，材料模型选用双线性随动强化模型(BKIN)进行计算，选用Mises屈服准则和随动强化准则，本构关系采用双折线完全理想弹塑性关系。

图2 有限元模型

在拱桥极限承载力分析中，根据非线性稳定计算公式，将恒载和活载按照一定比例进行加载来考虑荷载效果，已有研究表明[13]，位移结果包含自重作用下的量，虽然这一结果与自重作用下结构初始状态由设计形状确定的实际情况不完全吻合，但是曲线拱肋在荷载作用下内力以轴力为主，结构变形相当小，所以此种加载方式对结构稳定性验算的影响也是可以忽略的。其中恒载由一期恒载和二期恒载组成，一期恒载按照结构自重计入，二期恒载按照设计值60 kN·m-1施加；列车活载加载中将双线中—活载等效为均布线荷载施加；桥梁的风荷载仅考虑横向风力作用，其受风面积按照结构轮廓面积乘以0.4进行折减。

3 大跨度铁路下承式钢桁梁柔性拱桥稳定性分析

3.1 考虑几何初始偏位的弹性稳定分析

首先对大跨度铁路下承式钢桁架柔性拱桥的各个工况进行第1类稳定分析[14]，即弹性稳定分析，获取结构失稳的一般特征，包括屈曲模态和屈曲荷载大小。考虑到桥梁桁架杆件在制作、拼装以及焊接等施工过程中带来误差从而造成桥梁结构的初始几何偏位，研究表明[14-15]通过采用模态变形法施加结构的几何初始缺陷对结构的稳定承载力产生的影响最大。在此，对下承式钢桁架柔性拱桥的4个施工阶段及运营阶段的11种荷载工况的开展弹性稳定分析。为进一步分析桥梁结构的初始几何偏位对稳定的影响，将对应失稳模态下的最大节点位移取值k(k值分别取l/3 000，l/2 000和l/1 000，l为计算跨径)，作为结构的节点位移偏差施加于桥梁结构各节点，分析相应几何初始偏差对桥梁结构稳定系数的影响。计算中，还将k取0值，即不考虑初始几何偏位的影响作为对比分析。部分受力不利工况的计算结果见表1。

表1 各工况下弹性稳定分析结果

由稳定分析可知：不同工况时，桥梁结构的稳定系数亦不同，活载布置位置对结构的稳定性影响较大，通过桥梁的失稳模态可以看出拱肋整体面内失稳而导致整个结构失稳。由于拱肋的采用整体吊装，则在安装拱肋阶段钢桁梁承担的施工荷载较小，施工阶段的稳定性比较高，且稳定系数均大于运营阶段的系数，其中结构在运营阶段的恒载+单主跨满载+对侧边跨满载+风载工况(以下简称工况Ⅰ)稳定承载力最低，系数为10.152，恒载+主跨满载+风载工况(以下简称工况Ⅱ)次之，系数为10.641。

对比表1中结果可知在考虑安装和制造误差时，结构在施工和运营阶段的稳定系数都会降低，其中在施工阶段的拱肋吊装后吊杆张拉前工况稳定系数由19.185降低至15.578，降低18.80%；在稳定性最低的运营阶段恒载+左主跨满布荷载+右边跨满布荷载+风荷载工况稳定系数由10.152降低至9.245，降低8.93%。由表1还可知，初始缺陷会导致结构的稳定性降低，且稳定系数随初始缺陷的增加降低速度明显加快。

3.2 考虑几何及材料非线性的稳定性分析

由大跨度铁路下承式钢桁架柔性拱桥结构的弹性稳定分析可知，工况Ⅰ(恒载+单主跨满载+对侧边跨满载+风载)的稳定系数最低，故以此工况对桥梁开展非线性稳定进行分析，即第2类稳定分析。分析时采用了单独考虑几何非线性和同时考虑几何和材料的双重非线性2种分析方法，其中材料非线性为桥梁钢材均采用理想弹塑性的材料本构关系，即钢桁梁、拱肋、纵横梁钢材受力达到屈服强度(主结构370 MPa、联结系340 MPa)后为理想塑性变形材料。在分析过程中初始几何偏位施加方式与第1类稳定分析相同，仍然选取的k值分别为0～l/1 000。各个工况下的非线性稳定分析结果见表2和图3。

表2 各工况下非线性稳定分析结果

图3 不同工况下稳定系数与拱顶位移关系曲线

计算结果表明，在k=0仅考虑结构几何非线性后，结构的稳定系数相对弹性阶段减小了1.069，稳定性降低了10.52%，只考虑结构的大变形且不考虑几何缺陷时结构的稳定性降低很小；当k=l/3 000时，稳定系数降低5.29%，而k=l/1 000时，结构的稳定系数降到7.843，稳定系数降低13.66%。由于采用的几何缺陷的量值比较小，所以结构的稳定安全系数只有很小的减幅，但是稳定性会随着缺陷的增大减小，且减小幅值将会更大。

在考虑几何及材料双重非线性后，结构的稳定系数降低很明显。当k=0且考虑材料和结构几何非线性时，结构稳定系数为2.65，分别比完全弹性和仅考虑几何非线性的系数降低71.1%和70.8%，可见弹性稳定和仅考虑几何非线性分析时过高地估计了结构的稳定性，进行桥梁的稳定性分析时必须考虑非线性才能得到与真实承载力相对接近的结果。经过对比不同缺陷结构的稳定性，可以发现缺陷在一定程度上降低结构的稳定性且随缺陷的增大降低比例越大，但是降低的比例是有限的。通过对各工况的每个荷载步进行追踪发现，结构在荷载加至2.30倍时，结构在边跨支座处下弦杆和中跨的支座相连的上弦杆出现了塑性；随着荷载继续加大，主跨的跨中处下弦杆发生塑性变形，整体结构的塑性区逐渐扩大，结构整体刚度也随之下降；当加载至2.60左右时，结构拱脚处杆件相继出现塑性变形，塑性区迅速扩大，随之结构失去承载能力，导致结构发生破坏。

4 稳定影响参数分析

大跨度铁路钢桁梁柔性拱桥作为复杂的空间结构，在双线中―活载下其稳定性受到多种因素的影响。根据该类桥型的特点，在考虑结构几何和材料双重非线性的基础上，再将横向位移、不同材料非线性、温度等影响因素计入，分析各个参数变化对结构稳定性的影响。

4.1 拱肋横向初始偏位对结构稳定性的影响

随着铁路钢桁梁柔性拱桥主跨跨径的增大，其杆件的横向尺寸和竖向高度也将会增大，拱的矢高也会更高，且规范中规定的桁架拱桥的横向受风面积取值一般较大，从而造成横向风作用下桥梁稳定问题也将越来越突出，因此研究结构在不同风荷载下的稳定性就很有必要。将横向风荷载引起的位移作为初始横向位移，即拱顶的初始横向偏位取值介于l/3 000～l/1 000之间，研究在不同初始位移条件下，结构的稳定系数与初始横向位移的关系。工况Ⅰ下初始横向位移对铁路钢桁梁柔性拱桥的稳定性影响结果见表3，在不同横向初始偏位下的稳定系数与拱顶位移曲线如图4所示。

从计算结果可知，初始横向偏位的施加会导致结构的稳定系数降低，但是初始横向位移对铁路钢桁梁柔性拱桥稳定性的影响不大，结构稳定性下降是由于拱肋由以受压为主转化为弯压共同作用。在结构考虑双重非线性条件下，当初始位移采用l/1 000时，其稳定性下降最明显，相对没有考虑初始横向位移的稳定系数降低5.66%。同时可以发现，如果横向位移相对较小时，即横向风荷载较小时，其对结构稳定性的影响可以忽略不计。由图4还可以发现，结构的拱顶竖向位移随横向初始位移的施加呈现明显的非线性效应。

表3 各工况下结构稳定分析结果

图4 不同横向初始偏位下稳定系数与拱顶位移关系曲线

4.2 材料非线性对桥梁稳定性的影响

为了探究桥梁不同构件的非线性对稳定承载力的影响，考虑4种不同情况：情况Ⅰ，考虑全桥主要受力杆件钢桁梁、拱肋、纵横梁的材料本构关系采用理想弹塑性，其余次要杆件采用理想弹性；情况Ⅱ，仅考虑钢桁梁的材料为理想弹塑性，而其余杆件采用理想弹性；情况Ⅲ，仅考虑拱肋为理想弹塑性，而其余杆件采用弹性；情况Ⅳ，仅考虑纵横梁的材料理想弹塑性，而其余杆件采用完全弹性。计算结果见表4，在不同构件非线性下的稳定系数与拱顶位移关系曲线如图5所示。

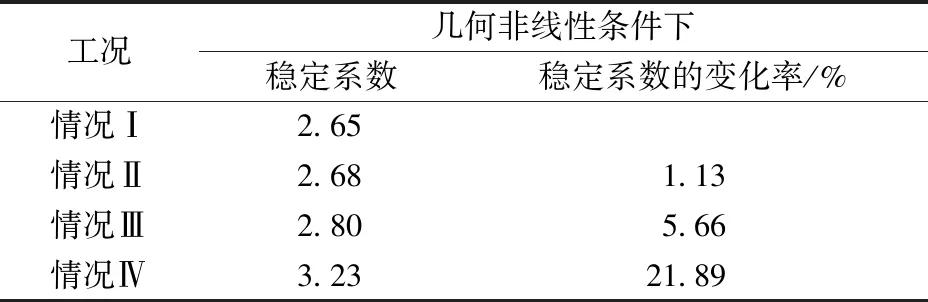
表4 各工况下结构稳定性分析结果

由表4可见，情况Ⅰ和Ⅱ下结构的稳定性基本一致，稳定系数增加1.13%，情况Ⅲ和Ⅳ与情况Ⅰ差距较大，稳定系数增加5.66%和21.98%，这也说明随荷载增大结构中的钢桁梁杆件首先发生塑性破坏，随后是拱肋杆件发生塑性破坏，最后是纵横梁杆件发生破坏。因此钢桁梁材料的非线性对结构的稳定性影响最大，其中在纵横梁产生破坏之前，钢桁梁和拱肋已经发生破坏，所以纵横梁的材料非线性对结构稳定性的影响可以忽略。研究也表明提高钢桁梁局部杆件的屈服应力，将推迟结构进入塑性状态，有利于提高结构刚度和稳定性。

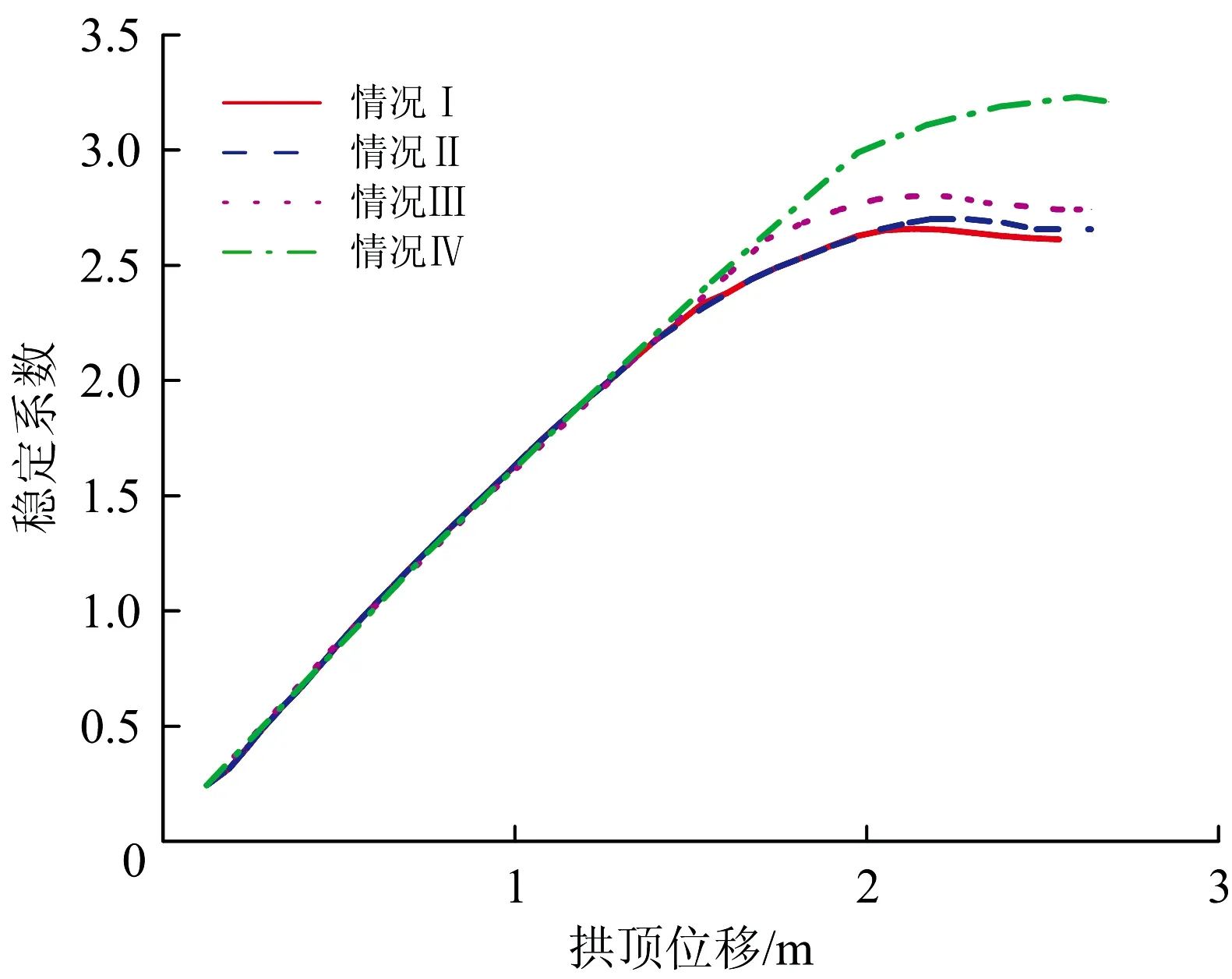
图5 不同构件非线性下稳定系数与拱顶位移关系曲线

4.3 温度变化对桥梁稳定性的影响

为考察温度变化对结构稳定性的影响，分析3种工况：原工况，恒载+隔跨满布双线列车荷载；升温60 ℃工况，恒载+升温60 ℃+隔跨满布双线列车荷载；降温15 ℃工况，恒载+降温15 ℃+隔跨满布双线列车荷载，钢结构温度主要参照广州最低和最高温度。各个工况的稳定系数计算结果及对比见表5，稳定系数与拱顶位移关系曲线如图6所示。

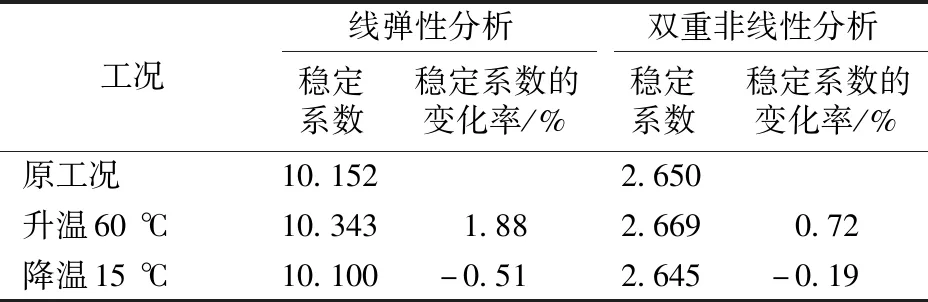
表5 各工况下结构稳定性分析结果

结果表明，温度变化会对稳定性产生一定影响，但总体影响较小。按弹性理论分析，工况Ⅰ、工况Ⅲ的稳定系数分别为10.343和10.100，相对工况Ⅱ的稳定系数增大1.88%和-0.51%；考虑双重非线性时，工况Ⅰ、工况Ⅲ的稳定系数分别为2.669和2.645，相对工况Ⅱ的稳定系数增大+0.72%和0.19%，因此升温时可略提高下承式钢桁梁柔性拱桥的稳定性，降温时将略降低该类型桥梁的稳定性。

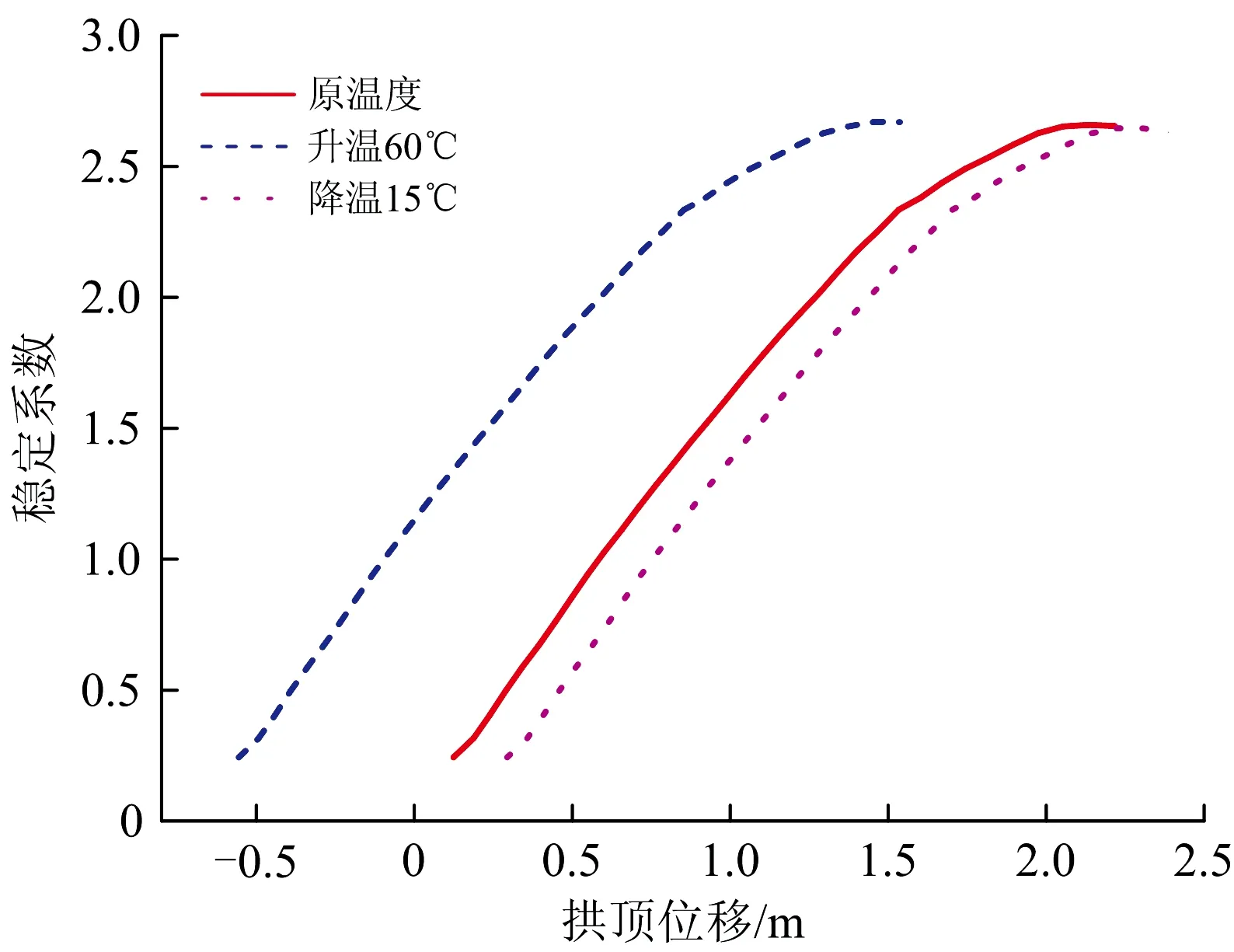
图6 不同温度下稳定系数与拱顶位移关系曲线

5 结 论

(1)从下承式钢桁梁柔性拱桥的第1类稳定分析结果可知，施工阶段结构的稳定性普遍较高，其中施加二期恒载后的成桥阶段，结构的稳定安全系数最低为13.319，钢桁梁合拢前阶段次之，系数为15.811；在运营阶段桥梁结构的恒载对结构稳定性影响最大，活载次之，失稳形式表现为拱肋的整体面内失稳。

(2)仅考虑几何非线性时，结构的稳定系数为9.083，对比按照弹性理论分析的稳定系数降低10.58%；当考虑k取l/3 000，l/2 000和l/1 000的几何初始偏位时结构的稳定系数分别仅下降5.29%，6.83%和13.66%。

(3)当考虑几何和材料双重非线性时，桥梁的稳定系数较弹性稳定系数下降显著，不考虑几何初始偏位时稳定系数为2.654，相比线弹性和仅考虑几何非线性的稳定系数分别降低73.90%和70.81%；当进一步考虑结构存在k为l/3 000，l/2 000和l/1 000的几何初始缺陷条件下，相对双重非线性的稳定系数分别减小1.89%，4.91%和9.81%，因此在求解钢桁梁柔性拱桥的稳定系数时，应考虑结构的双重非线性。

(4)材料非线性对桥梁稳定系数影响最明显，在该桥的稳定分析中钢桁梁的部分杆件最先失稳，拱肋次之，钢纵横梁最后失稳，所以提高钢桁梁局部杆件材料的强度将推迟结构进入塑性状态将有助于提高结构的稳定性；温度变化将对结构的稳定性产生一定的影响，但影响较小。各种因素下下承式钢桁梁柔性拱桥最不利稳定系数为2.39，总体稳定性良好。