基于压缩感知的CT重建算法的研究进展

尹娟，范医鲁，秦绍华

1. 山东省千佛山医院 医学工程部，山东 济南 250014；2. 山东师范大学 物理与电子科学学院，山东 济南 250358

引言

自从1927 年，英国工程师Hounsfield 研制成功第一台医用CT 装置以来，CT 在临床领域一直发挥着重要作用。Hounsfield 和Cormack 两位没有医学经历的科学家，也因为其在CT 领域的开创性工作，在1979 年被授予诺贝尔生理或医学奖。CT 技术主要是利用X 射线穿透物体的衰减信息来进行物体断层图像信息的重建[1]。从投影重建图像本质上属于数学反问题，重建算法是CT 技术的核心理论问题。

1 传统的CT重建算法

CT 是通过具有一定能量和穿透能力的X 射线与物体相互作用的原理而成像的。如当一定能量的X 射线穿过物体时，X 射线的强度会发生衰减，其衰减程度与物体的成分、

厚度有关，如果物体是均匀的，X 射线的强度按指数规律衰减，遵循Lambert-Beer 定律：

其中I0位射线原始强度，I 为射线穿透物体后的强度，μ 为被测物体的衰减系数，l 为射线穿过物体的长度。

如果物体是非均匀的，如图1 所示，假设其衰减系数分布为μ(x,y)，则其衰减程度为沿投射路径L 的线积分

投影数据b

图1 X射线穿过非均匀物体示意图

CT 重建就是根据投影数据b，求解μ(x, y)的过程。CT重建算法主要分为解析类（Analytic Reconstruction，AR）和迭代类（Iterative Reconstruction，IR）。解析类重建算法以Randon 变换为理论基础，经过长期的发展，目前已经形成了完整的理论体系。解析类重建算法主要包括二维图像重建的滤波反投影算法（Filtering Back-Projection，FBP）和三维图像重建的FDK 算法。FBP 算法一直都被作为CT重建算法的基础和“金标准”。解析类重建算法发展时间较长，具有分辨率高、重建速度快等优点，但是抗噪声性能较差，对数据的完备性要求较高。

迭代类重建算法将测量得到投影数据作为已知量，将重建图像作为未知量，建立方程组，通过解方程来重建未知图像。设图像X 有M 个像素，投影数据B 有N 个测量值，则图像X 和投影数据B 之间的关系用方程组可以描述为

2 基于压缩感知的CT重建算法

近年来，为了减少X 射线对于病患的危害，对减少CT 扫描的时间和降低扫描的强度提出了新的要求[4-5]；同时随着CT 应用场景的扩展，有些应用也需要快速成像或者减少CT 扫描的角度。这都导致CT 投影数据的不完整，如何在投影数据不完整的条件，保证CT 重建图像的质量，是CT 重建算法面临的新挑战。

2.1 压缩感知理论

压缩感知理论（Compressed Sensing，CS）是一项不同于传统数据处理技术的全新理论，其发展以2006 年Donoho[6]在理论上取得的重大突破为标志，目前压缩感知理论正在快

如果观测阵满足RIP（Restricted Isometry Property）特性，那么可以从压缩后的观测数据准确地恢复出信号。如果观测阵是高斯随机矩阵或贝努力矩阵，那么M 的下限是

其中C 为一正常数。正常情况下，由于M＜N，从y 恢复x 是不可能的，但当满足x 的稀疏性和观测阵的RIP 特性要求时，可以利用非线性优化的方法完美的恢复出信号，即：

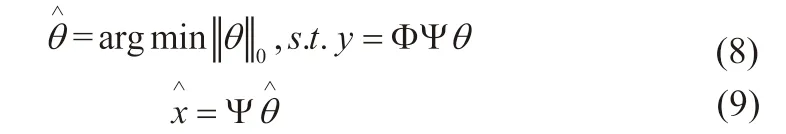
常用的恢复算法有凸优化算法和贪婪算法两类，凸优化算法的代表是BP（Basis Pursuit）算法[7]，贪婪算法包括MP（Matching Pursuit）算法[8]、OMP（Orthogonal Matching Pursuit）算法[9]和CoSaMP（Compressive Sampling Matching Pursuit）算法[10]等多种算法。

2.2 基于压缩感知的重建算法

在投影数据不完整的条件下，传统的重建算法在重建速度和重建精度方面都无法满足实际应用的需求。压缩感知理论为不完整投影数据重建问题提供了新的思路。一方面，压缩感知理论对信息的采集位置没有要求，另一方面，压缩感知理论对于信息的采集数量要求较低，这使得根据不完整数据进行CT 图像重建成为可能。综合公式(4)、(8)、(9)，可得到基于压缩感知的 CT 不完整投影数据重建过程如下

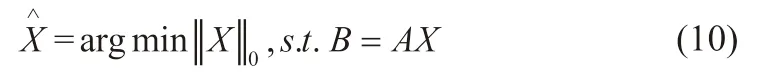
这个问题可以通过转化为优化问题求解

g(x)为正则化项，在投影数据不完整条件下，通过数据保真度重建图像，在数学上属于一个不完备方程求解，需要添加先验知识来作为正则项，对优化过程进行约束。正则化可以分为基于图像稀疏化的方法，以及利用先验图像约束的方法两大类[11-14]。常用的稀疏化有L0 范数，L1 范数，TV（Total Variation）以及字典学习等不同方法，先验图像包括人体解剖结构，患者早期的医学影像信息以及其他模态信息。优化问题的求解可以通过近端算法（Proximal Algorithms）实现[15-17]。

2.2.1 基于图像稀疏化的 CT不完整投影数据重建

图像稀疏化可以分为基于范数和基于字典等不同方法。L0 范数和L1 范数是传统的正则化方法，广泛应用于各种信号稀疏化场景。近年来，随着对图像特点的分析，基于图像梯度L1 范数的TV 方法，在图像稀疏化过程中获得了广泛应用。2008 年Sidky 等[18]利用TV 最速下降法和凸集投影约束相结合的方法进行了CBCT 图像重建。近几年，许多研究者基于TV 方法，对CT 图像重建算法进行了改进[19-21]。2015 年Hongliang 等[22]将基于L1 范数的TV 形式与基于L0范数的TV 形式相结合，代替传统的基于L1 范数的TV 形式，有效改善了CT 重建效果。但是TV 方法用图像的梯度特征来稀疏图像，无法区分图像的结构信息和噪声，容易出现光滑过度的现象，造成CT 图像器官轮廓和纹理的模糊。

字典学习是一种有效的图像稀疏方法，其通过对图像进行训练的方法，得到适合图像稀疏表示的字典[23]。近几年，许多研究者尝试利用字典学习的方法稀疏化CT 图像，进行重建。2012 年，Xu 等[24]用字典学习的方法，对低剂量CT图像进行了重建。2014 年提出的ASDL 算法[25]，在字典学习的过程中，综合考虑图像的方向和尺度信息，来消除CT 图像中的伪影，改善重建效果。2015 年，Shi 等[26]根据CT 三维图像的特点，综合考虑图像的空间和时间相关性，建立三维字典学习方法，有效提高了CT 图像的重建效果。由于字典学习的方法在字典训练过程中，将图像先分块学习，再合并处理。因此容易产生块状噪声。字典学习方法在分块过程中，并没有考虑图像块之间的空间相关性，因此其稀疏化效果和对图像结构信息的保护程度还有待提高。

2.2.2 基于先验图像的CT不完整投影数据重建

CT 不完整投影数据重建问题，从数学本质上属于欠定方程的求解问题，先验知识的增加有利于方程的求解。人体解剖结构，以及患者其他医学影像信息，都可以作为先验知识，改善CT 重建效果。加入先验知识的CT 重建过程可以表示为

其中u 为先验图像，h(x-u)表示先验图像与重建图像的差值，为权重系数。先验知识可以为重建过程提供更多的信息，有利于重建进行，但是先验图像与真实图像是不同的，如果重建过程过分依赖先验图像，则会掩盖重建图像的细节信息，如果先验图像的权重过低，则对于重建图像的改善效果有限，因此在重建过程中，如何平衡先验图像的权重是一个关键问题。

2008 年，PICCS 算法利用压缩感知理论，对基于先验图像的CBCT 不完整投影数据重建问题进行了研究[27]。此后，许多研究者在此基础上，进行了进一步探讨。2015 年提出的pPICCS 算法[28]，针对配准对CT 图像重建效果的影响进行了研究，对PICCS 算法进行了改进。2015 年，Lubner 等[29]对PICCS 算法在腹部CT 图像上的重建效果进行了分析，从临床应用的角度，对减少CT 照射剂量和保证图像质量的平衡问题进行了研究。2017 年约翰霍普金斯大学的Stayman 也对应用CT 图像作为先验知识，对CBCT图像的质量提升问题进行了研究，并对先验知识的权重问题进行了分析[30-32]。先验知识的加入，有助于CT 不完整投影数据的重建。但是患者先期获得的图像与当前的CT 图像存在一定的差异，这对基于先验图像的CT 不完整投影数据重建的精度，造成了一定的影响，如何有效地利用先验知识是基于先验知识的CT 不完整投影数据重建的关键。

3 总结

基于压缩感知理论，在CT 重建过程中应用迭代算法，可以有效地减少CT 扫描的剂量和角度，具有很好的发展前景。近年来，随着人工智能的发展，应用深度学习网络来解决CT 重建问题，也引起了业内学者和厂商的重视[33]。基于深度学习网络的启发，卷积稀疏编码近年来开始用于图像稀疏化，基于卷积稀疏编码的CT 重建算法也开始用于CT 重建[34]。深度学习网络和卷积稀疏编码在CT 重建算法中的应用，有效地提高了CT 图像的质量，但是深度学习网络的参数，以及卷积稀疏编码的字典都需要从大量的数据中学习得到，需要强大的运算能力和时间保证，以及病人大数据信息的保证，这些都增加了其在实践中应用的难度。基于深度学习网络和卷积稀疏编码的CT 重建算法同样面临投影数据不完整的问题，如何将压缩感知理论，与深度学习网络和卷积稀疏编码等技术相结合，有效地提高CT 重建质量，是基于压缩感知的CT 重建算法面临的重要问题。