基于排队模型的航天器环模设备负载能力分析

2019-08-20李西园封宝华张丽娜

航天器环境工程 2019年4期

李西园，封宝华，张丽娜，王磊，王晶,3

（1. 北京卫星环境工程研究所，北京 100094； 2. 北京航空航天大学航空科学与工程学院，北京 100191；3. 可靠性与环境工程技术重点实验室，北京 100094）

0 引言

航天器系统、各单机均需要在空间环境模拟（环模）设备内部进行真空热试验[1]。根据标准要求，热平衡试验至少包括极端高温和极端低温2个工况，热真空试验则至少包括4个高、低温循环[2]。一般而言，大型组件的真空热试验对空间环模设备的占用时间可达1周甚至1月以上。我国的空间环模设备建设主要由航天重大型号牵引，着眼于满足载人飞船、空间站舱段等特殊航天器研制的需求[3]。近年来，随着导航、通信、遥感等卫星的并行研制和高密度发射，在各种规模的空间环模设备中均出现过试验进度冲突的现象。目前，针对试验等待的情况一般只能通过流程优化、管理优化的方式提升试验效率[4]，以尽量缩短等待时间，而缺少通过数学、统计学方法评估设备负载能力、优化试验进度安排、指导设备建设规划的相关研究。

排队论属于数学中运筹学的分支学科，其主要研究服务系统中排队现象的规律[5]。通过统计服务对象到达间隔和服务时间的分布，得出平均排队长度、排队时间等关键指标的统计规律，并以此为依据改进系统设计[6]，使系统实现承载能力、效率的最优。目前排队论已经被广泛应用于服务行业优化[7]、通信系统接口改进[8]、道路负载能力计算[9]等过程中。

本文针对某系列中型空间环模设备的最大负载问题，统计近5年间该系列设备的系统启动、关闭时间，基于M/G/k/∞/∞/FCFS模型建立其排队模型，并通过蒙特卡罗方法计算出不同任务量、不同试验持续时间分布下的仿真结果。该排队模型可以给出系列化空间环模设备在不同任务量、不同试验持续时间分布下的试件平均排队长度、平均排队时间等关键指标，用于评估未来任务量增多时的环模设备利用率，为设备建设规划提供参考。

1 仿真模型

1.1 系统模型

例某大型AIT试验大厅共有4台供同时开展试验的中型空间环模设备，太阳电池板、天线、微小卫星及其他试件依次排队等待空闲设备进行真空热试验。

一般的航天器及组件真空热试验可以分为试验设计、试验准备、试验进行、试验撤收、试验数据整理几个阶段，其中在试验准备、试验进行和试验撤收阶段需要完全占用空间环模设备，期间不能进行其他试验。统计空间环模设备测控系统的启动、关闭时间是准确统计试验时间的一种有效方法[10]。本文统计了2014年至2018年共计237次调试与试验任务的测控系统启动、关闭时间，其中间隔5天以上的同名试验按照2次试验计算，启动、关闭时间接近且占用同一容器的多个试验（一般为搭载试验）按照1次试验计算。试验对空间环模设备占用时间T1与测控系统运行时间T2的关系如图1所示：T1=t1+t2+t3，T2=t2+t3。本文按照T1=1.5×T2来估算环模设备占用时间，即认为对测控系统占用时间长的复杂试验，其试验准备时间也线性增加。

2014年至2018年237次试验任务的试验间隔时间、试验持续时间统计结果见表1。

表1 试验间隔时间与试验持续时间统计Table 1 Statistics of test pieces arrival time and test duration

1.2 试验间隔时间分布

在排队模型中，试验间隔时间分布一般有确定型（D）、负指数型（M）和k阶埃尔朗（Ek）分布等，其中以负指数分布最为常见。图2所示为本文统计的试验间隔时间分布与负指数分布曲线的对比，可以看到二者较为接近。

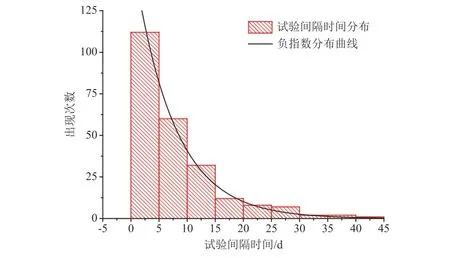
图2 试验间隔时间分布Fig.2 Distribution of test intervals

Kolmogorov-Smirnov方法可基于累积分布函数，检验一个经验分布是否符合某种理论分布或比较两个经验分布是否有显著性差异[11]。本文统计的试验间隔近似服从θ=7.19的负指数分布，其中参数θ的标准误差为0.47，K-S检验结果参数p为0.13，即选择显著性水平α=0.05时，不能拒绝试验间隔时间服从负指数分布的假设，其概率密度为

式中θ为负指数分布的尺度参数。当试验间隔时间分布服从负指数分布时，可以认为试件到达为泊松流，即单位时间内到达的试件数量n服从泊松分布

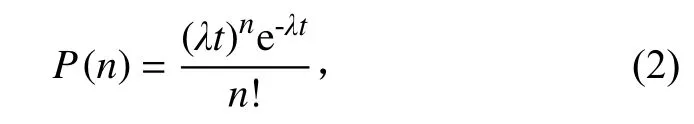
式中λ为单位时间内随机事件的平均发生次数，取为1/θ。

图3为月平均试件到达数量分布统计与泊松分布的对比，可以看到单位时间内达到的试件数量近似服从泊松分布，表明对于试验间隔时间服从负指数分布的假设是合理的。

图3 月平均试件到达数量分布Fig.3 Distribution of the number of monthly arrived test pieces

1.3 试验持续时间分布

在排队模型中，服务时间分布一般有指数型（M）、一般型（G）和k阶埃尔朗（Ek）分布等，其中一般型包括正态分布、Gamma分布等形式。图4为本文统计的试验持续时间分布与负指数分布、截断正态分布、Gamma分布的对比，并进行K-S检验，结果见表2。表中：θ为负指数分布的尺度参数；μ、σ为截断正态分布的位置参数和尺度参数；α、β为Gamma分布的形状参数和尺度参数。

如表2所示，当显著性水平α=0.05时，不能拒绝试验持续时间服从Gamma分布的假设，其概率密度为

图4 试验持续时间分布Fig.4 Comparison among distributions of test duration

式中，Gamma分布的形状参数α、尺度参数β的拟合值分别为3.05和3.15。

1.4 排队模型构建

试件排队进行真空热试验的排队模型（图5）可以用M/G/k/∞/∞/FCFS模型描述，即：试验间隔时间服从负指数分布，试件占用空间环模设备的时间服从Gamma分布，队列为单一队列多服务台模型，系统容量和试件数无限制，排序规则为先到先服务规则。

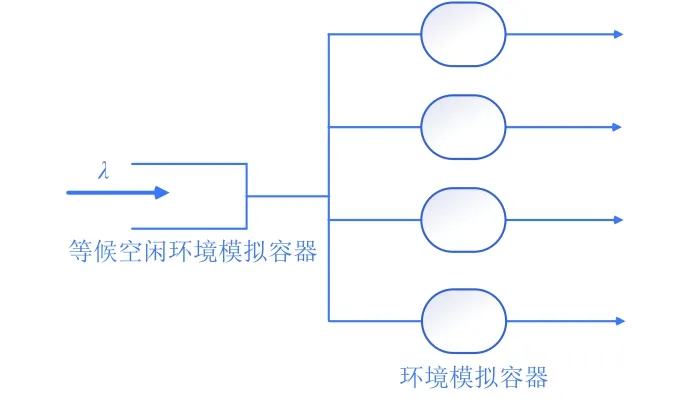
图5 真空热试验试件排队模型Fig.5 Queuing model for the test pieces

目前对于M/G/k排队模型尚没有公式化的推导过程，平均排队时间和平均排队长度等指标亦没有明确的数学表达式，可采用近似公式给出[12]，但对于不同排队长度的概率，则较难通过经验公式求解。本文通过MatLab建立了试件排队进行试验的蒙特卡罗仿真模型，对比不同的试验持续时间分布对于仿真结果的影响。仿真工况如表3所示（其中任务量比以现有任务量下的θ=7为基准）。

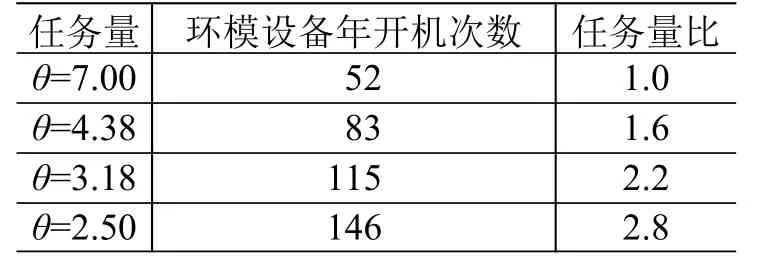
表3 排队模型仿真工况Table 3 Simulation cases

2 计算结果分析

本文通过蒙特卡罗方法分别对每个计算工况进行了100次仿真，仿真中的试验持续时间分布分别采用负指数（Exp）分布、截断正态（Norm）分布和Gamma分布。统计排队模型关键指标平均值见表4，表中：W为试件在试验大厅的停留时间；Wq为试件在试验前的平均排队时间；Ws为试件的平均试验时间；Lq为试件平均排队长度；N为排队系统中的平均试件数，取等待中试件和试验中试件数量之和。同时，对工况中试验大厅内无空置环模设备的概率Pfull进行了统计。

表4 不同任务量下排队模型仿真的关键参数统计Table 4 Analysis of key parameters of queuing models with different test task numbers

为了对蒙特卡罗模型的收敛性进行评估，引入离散系数，对于一组仿真中获得的排队模型关键参数样本x，其可以表示为

式中：SD(x)为样本的标准差；为样本的平均值。通过离散系数可以对多组平均值、单位不同的样本进行离散度比较，统计排队模型关键指标仿真值的离散系数如表5所示。可以看到，对于所有计算工况，多次蒙特卡罗仿真获得的结果非常接近，排队模型关键参数的离散系数均小于0.05，可以认为结果已经收敛，即本文通过蒙特卡罗法求解的结果可以代表该排队模型的关键参数。

表5 排队模型关键参数仿真值的离散系数Table 5 Coefficients of variation for key parameters of the queue model

图6为不同任务量下根据3种试验持续时间分布所计算的试件排队长度分布。由图可见：任务量较低时，不同的试验持续时间分布对试件排队长度分布影响非常小；但随着任务量的增大，负指数分布的试验持续时间分布逐渐与截断正态分布和Gamma分布产生差异。

图6 试件排队长度分布Fig.6 Distribution of queue length

图7和图8为不同任务量、不同试验持续时间分布下，试件进行试验前的平均排队长度、平均排队时间以及试验大厅内无空置环模设备的概率。可以看到：在空间环模设备负载量相对较低时，由于不同试验持续时间分布的数学期望一致，排队时间、排队长度等关键指标并无差异；随着任务量的增大，试验持续时间的分布对平均排队长度和平均排队时间均会产生影响，其中截断正态分布与Gamma分布的计算结果较为接近，负指数分布的计算结果则偏差较大。这表明，针对真空热试验的试件排队问题，应选取与实际情况最为接近的Gamma分布或截断正态分布。此外，当试验持续时间分布不发生变化时，若任务量继续上升，在达到当前任务量的2倍前，平均排队长度、平均排队时间随任务量的增加缓慢增加；但若任务量达到当前任务量的2.4倍以上时，平均排队长度、平均排队时间上升斜率迅速变大，现有设备将难以满足全部试件的进度要求。