神经网络技术在P2P网贷中小企业信用评估中的应用

李淑锦，潘雨虹

（杭州电子科技大学 经济学院，浙江 杭州 310018）

一、引言

科技信息媒介与金融业务的融合创新产生了典型P2P网络融资模式。作为一种跨时间、跨空间的资金借贷新模式，在当前的金融体系下，P2P网络借贷的出现有效地解决了不同地区市场投资者对收益和风险的不同偏好，以及市场中长尾人群对融资的规模化需求。

改革开放以来，中小企业已成为中国经济的重要力量，其能否良好发展对中国经济的未来发展起着至关重要的作用。目前，全国中小企业总数已超过4 300万家，企业之间的竞争日趋激烈。在这场激烈的竞争中，解决中小企业融资难问题已经迫在眉睫。互联网背景下的P2P网络借贷一度被认为是解决中小企业融资难问题的有效途径，但如何有效识别P2P网络借贷平台上中小企业借款者的信用风险是科学管控与预防金融领域系统性风险的关键，也是促进金融生态系统可持续稳定发展的重要环节。

P2P作为第三方的借贷平台，一直备受学者们的关注。一部分学者研究了P2P网络借贷的发展历程和经营模式等。Galloway（2009）[1]就占据市场主要份额的Prosper借贷平台的主要经营模式进行了细致的讨论，特别强调了借贷双方通过信用凭证直接关联的经营模式，这种模式使平台负有对违约方欠债的追偿责任。刘文雅和晏钢（2011）[2]则从P2P的起源和网上信贷的具体运作方式入手，分析了我国网上借贷的模式，并对我国P2P网贷的发展予以展望。彭龙和闫琳（2018）[3]对比分析了我国P2P网贷与美国P2P网贷的发展状况，指出我国的P2P平台在运营理念、产品类型和风控模式等方面均与美国存在较大差异，而这些差异是为了适应我国的市场环境造成的。

另有一些学者对个人及其企业借款者的信用风险评估问题进行了研究。Ha（2010）[4]构建了结合Kohonen网络和Cox的比例风险的混合动态模型，研究结果表明该模型的预测准确度得分高于93%。Blanco等（2013）[5]采用来自秘鲁小额信贷机构的借款者的样本，基于多层感知器方法（MLP）构建了几个非参数信用评分模型，与其他采用传统线性判别分析（LDA）、二次判别分析（QDA）和逻辑回归（LR）的模型进行了比较，结果显示神经网络模型错误分类成本方面均优于其他三种经典技术。还有一些学者们研究了P2P网络借贷平台上借款者的信用风险评估问题，如Allen等（2007）[6]实证发现P2P借贷平台上小额贷款的风险会受到借款人的年龄、家庭净资产、性别等的影响。国内学者宋丽平等（2015）[7]认为个人借款人的历史表现、客观条件和还款能力将对P2P网贷的个人借款人的信用风险产生重要影响。刘红娟（2017）[8]从五方面构造了P2P供应链模式下的中小企业的信用评估指标体系，用BP神经网络与Logistics方法对其信用风险进行评估，结果表明BP神经网络的预测能力高于Logistics回归。

还有部分学者将多层感知器与径向基函数应用于企业信用风险的评估问题。如庞素琳和王燕鸣（2003）[9]利用公司经营状况的四个主要财务指标，通过多层感知器对96家上市公司进行分类，准确率达到79.17%。高国平和刘树安（2007）[10]通过综合分析国内外企业信用评分指标体系，建立了基于径向基函数神经网络的信用评分模型，利用辽宁华诚信用评级有限公司的相关数据分别进行判别和分析，得到了令人满意的评价结果。在众多研究成果中，尚未发现有学者把这两种方法应用于P2P借贷平台上的中小企业借款者的信用风险评估。

综上所述，神经网络技术在信用风险评估中具有很好的预测精度。文章试图将多层感知器与径向基函数这两种神经网络方法用于P2P借贷平台上的中小企业的信用风险评估中，且对两种方法的评估结果进行对比分析，突出其在中小企业信用风险评估预测的能力。在大数据的背景下，通过企业信用风险评估理论建立中小企业的信用风险评估指标，并拟使用Python技术获取P2P借贷平台的中小企业借款者的数据，克服在中小企业信用风险评估中缺乏数据的缺点，解决中小企业信用风险评估问题。

文章的创新点之一是建立中小企业评估指标体系时考虑了行业的违约率；创新点之二是利用多重填补方法模拟出符合样本的数据并与神经网络算法相结合，使得结果可行性提高；创新点之三是将多层感知器与径向基函数进行结果对比分析，选择更适合中小企业信用评估的方法。

二、相关理论及信用风险评估指标选择

企业信用风险评估问题一直是信用风险管理的热点。迄今为止，已有不少学者从理论、实证方法的角度对企业的信用风险进行评估。

信用风险理论模型可以分为基于期权理论的结构模型和基于违约强度的约化模型。Merton基于Black和Scholes建立的期权定价理论，提出了结构化模型。该模型将持有负债的企业看作债权人持有的证券，其股东则持有以该证券为标的看涨期权。当企业的价值高于其债权时，股东会选择行权以继续持有公司股份，反之则是公司破产并归属于债权人。与结构化模型不同，约化模型是基于市场易于获得的信息来进行研究。该模型是Jarrow和Turnbull提出，经过Jarrow、Lando等诸多学者的不断完善。该模型将违约过程看作跳的过程，将违约时间选择在某个跳过程的首次跳时刻，而这种跳跃是不可预测的，即违约是一个不可预料的过程。

在结构化模型的应用中，众多学者采用相关公司的股票数据来代表公司的总价值；在约化模型的应用中，许多学者利用市场中的信用违约互换（CDS）和债券价格计算公司的违约概率。但由于在P2P平台上收集的中小企业大部分均无上市股票，也未发行债券，因而结构化模型与约化模型均无法直接应用于中小企业的信用风险评估中。故文章选取影响公司股票价值以及债券价格的相关指标，并参考学者Allen等的研究，选择企业所有者的特征指标如年龄、性别、学历、孩子个数、婚姻状况、房屋数量、汽车数量；中小企业经营状况的相关微观指标包括规模、投资者数目、营业收入；融资信贷指标包括借款金额、借款利率、借款目的、借款等级、其他贷款平台数量、其他平台借款、在点融网上的拖欠金额共17个微观指标以及居民消费指数CPI、国内生产总值GDP、狭义货币供应M1、财政支出、经济景气指数ECI、消费者信心指数CCI、失业率指数URI、采购经理指数PMI、国房景气指数CERCI和行业状况共10个宏观经济指标建立中小企业的信用风险评估指标体系。

企业所有者对企业的日常经营决策起着至关重要的作用，在不同的年龄阶段，其所倾向的决策也会不同，而决策会随着年龄的增长从激进型向稳健型转变，从而影响企业的发展；性别的不同、教育程度以及婚姻状况使得企业所有者在决策的偏好以及日常处理事情的方法上会呈现差异，从而影响企业发展；作为孩子的父亲或母亲，都希望给孩子提供好的生活条件，基于这个目的会使得企业所有者更用心、尽力地谋划，从而有利于企业的发展；而房屋数量与汽车数量作为反映企业所有者自身拥有的财产的指标，间接反映了企业的盈利能力。

企业的规模是反映企业业务成熟能力的一个指标，规模越小，其业务涉及的资金量也会越少，企业还款的困难度较高；投资者数目反映了外界投资者对企业未来发展的一个预测，数目越多表明该企业未来发展前景较好；企业的营业收入越高，企业违约的可能性便会越小；由于借款期限大多为12个月并且需要每月还款，当借款金额越高，所对应的借款利率也越高时，借款企业所承担的每月还款金额就越高，那么企业违约的可能性越大；借款的用处决定了资金的回收期的长短，将资金用于回收期长的项目时，前期资金链断裂的可能性增加，从而导致违约的发生。点融网根据中小企业借款者的资料，按照标准将借款者划分信用等级，等级高的借款者违约可能性较小，等级低的借款者违约可能性较大；其他贷款平台数量与其他平台借款均反映借款者的负债情况，借款者的负债越多，违约发生的可能性越大；在点融网上的拖欠金额越大，则表明借款企业对当时资金的缺乏程度越高，违约的可能性越大。

宏观经济状况也会影响中小企业的还款能力，如居民消费指数（CPI）通过反映消费者的消费能力，可以从侧面反映出市场需求情况。当需求较高时，企业的供给增加，营业收入也会相应的增加；国内生产总值（GDP）通常被视为衡量国家（或地区）经济状况的指标，该指标越高，反映出经济形势较好，违约率便会较低；作为反映货币供给的指标M1，其对经济的影响是双面性的，一方面货币供给的增加会导致利率水平的上升，使得借款者的还款金额相对变少，但另一方面高利率会使得物价水平的上升从而导致企业还款能力减弱；财政支出指标高显示政府对企业的业务支持会使得企业发展更加顺利，更利于企业还款；经济景气指数（ECI）是反映企业的生产经营以及经济运行状况，并预测未来经济的发展变化趋势的一个指标，与企业的经营发展相关；消费者信心指数（CCI）是反映消费者对当前经济形势评价和对经济前景、收入水平、收入预期以及消费心理状态的主观感受，与消费者未来的消费心理相关；失业率指数（URI）旨在衡量闲置的劳动产能，失业率越高，表明闲置劳动产能越高，经济形势较差，企业违约可能性较高；采购经理指数（PMI）反映了商业活动的现实情况，以及众多企业的相关经营情况，与企业是否违约相关；国房景气指数（CERCI）与企业所有者的资产以及企业拥有的固定资产相关；由于每个企业所处的行业不同，而在不同的行业中企业的生产模式、经营模式亦不同，资金周转期也不同，故文章选择行业状况作为影响其信用风险的宏观指标考虑。

三、方法介绍

文章使用预测能力较强的神经网络方法对中小企业的信用风险进行评估，可由于涉及的评估指标较多，意味着输入层的神经元节点太多，会极大地影响输出效率，而且指标之间也存在一定的关联性，故文章通过主成分因子分析提取公因子，实现指标分类降维的目的。在处理样本数据时发现存在部分信用指标数据缺失的现象，故需要对缺失数据进行填补处理。特别是缺失连续型变量，文章采用MCMC多重填补法。为了解决样本中违约样本与非违约样本占比不平衡的问题，采用SMOTE算法平衡数据。

（一）神经网络技术

神经网络技术的运算过程分为学习和工作两个阶段。在学习阶段，基于输入层的训练集数据，该算法会输出相关预期目标，并在获得具有最佳网络参数的模型后，模型可进入工作阶段。在工作阶段，将测试集的样本数据作为变量输入，基于神经网络模型在学习阶段所运行得到的参数以及该模型的运行规则，可以获得最终预测结果。神经网络技术是近年来的热点研究领域，其基本模型是多层感知器与径向基函数。

1.多层感知器。多层感知器包含1个输入层、1个或多个隐含层以及1个输出层，每一层都有若干个神经元节点。图1所示的是包含2个隐藏层的多层感知器模型。

图1 多层感知器结构

图2 径向基函数结构

多层感知器与径向基函数虽然均是前馈神经网络，但也存在不同，比如径向基函数只有1个隐含层，而多层感知器的隐含层可以是一层或者多层；多层感知器的隐含层和输出层具有相同的神经元模型，而径向基函数的隐含层神经元和输出层神经元不仅模型不同，而且在网络中起到的作用也不一样；径向基函数的隐含层是非线性的，输出层是线性的。然而，当用多层感知器解决模式分类问题时，它的隐含层和输出层通常选为非线性的；当用多层感知器解决非线性回归问题时，通常选择线性输出层。

基于此，文章将围绕这两种方法对点融网上的中小企业借款者的信用风险进行评估，通过对结果的对比分析，判断这两种方法在信用风险评估中的预测精度的强弱。

（二）主成分因子分析法

因子分析最早由英国心理学家C.E.斯皮尔曼提出，其基本目的是用少数因子来描述许多指标或因素之间的关系。因子分析涉及多种方法，如主成分因子分析、聚类分析、判别分析等。文章使用主成分因子分析方法。其计算步骤如下：

第一步，规范原始数据以消除变量之间数量级和量纲上的差异；

第二步，求出标准化数据的相关矩阵，并基于该相关矩阵，求出对应的特征值和特征向量；

第三步，计算方差贡献率和累积方差贡献率；

第四步，确定因子。设 F1，F2，…，Fp为 p 个因子，当其中前m个因子对数据信息量的累积贡献率不小于80%时，可以采用前m个因子来反映原始评价指标，若无法确定或意义不明显，则需要旋转因子以获得较为明显的实际含义；

第五步，采用Thomson估计，回归估计或Bartlett估计方法计算因子得分；

第六步，根据公式（1），以各因子的方差贡献率为权，通过各因子的线性组合得到综合评价指标函数，并对综合评分进行排序，得到评分名次。

其中，wj为旋转后因子的方差贡献率。

（三）MCMC多重填补法

多重填补是由Rubin在1978年首先提出的。多重填补法的具体方法较多，如针对连续型变量的预测均数匹配法、趋势得分法、马尔科夫链蒙塔卡罗（MCMC）方法等。考虑到文章样本的特殊性，采用MCMC方法，其具体操作步骤可分成两步：

第二步，后验。在每个周期中，从先前填补中得到的均值向量μ和协方差矩阵ε表示后验主体的对应值以模拟参数。循环填补和后验这两个步骤，可以生成足够长的马尔可夫链。当马尔可夫链集中在一个稳定分布时，就可以近似地从该独立分布中提出相应值进行填补。

（四）SMOTE算法

2002年Chawla提出了SMOTE算法，该算法的基本思想是对少数类别样本进行分析和模拟，并将新的人工模拟样本添加到数据集中，以避免原始数据中的类别严重失衡，其模拟过程采用KNN技术，模拟新样本生成的步骤如下：

第一步，采样最邻近算法，计算出每个少数类样本的K个近邻；

第二步，从K个近邻中随机挑选N个样本进行随机线性插值；

第三步，构造新的少数类样本，并将新样本与原数据合成，产生新的训练集。

四、信用风险评估过程及结果

（一）数据来源与指标赋值

文章的中小企业微观数据来源于P2P网络借贷平台——点融网。运用Python技术从点融网上获得1 392组数据，删除缺失起始时间的样本数据后，剩余1 385组数据作为样本。根据2004年6月巴塞尔银行监管委员会发布的《统一资本计量和资本标准的国际协议：修订框架》中对违约的定义：债务人对于银行集团的实质性信贷债务逾期90天以上即为违约。得出在1 385组样本中，违约样本为154个，非违约样本为1 231个，违约率为11.12%。这些样本涉及的行业较为广泛，其中餐饮业、零售业与服务业占比较大。样本的借款时间从2015年7月至2017年8月，大部分以12个月为借款期限，少部分则是贷款6个月、18个月。而在这些贷款中，每月归还贷款的借款企业占多数，只有个别贷款企业选择以双周还贷的形式。为了保证训练集和测试集的违约率与总样本一致，随机选择120个违约样本和965个非违约样本构成训练集，34个违约样本和266个非违约样本构成测试集。文章的宏观经济数据来自于国泰安数据库，行业指标数据来自工商银行、建设银行与农业银行的半年度报表数据汇总（中国银行未披露相关数据）。

由于指标数据的缺失率过高对违约预测会产生不利的影响，文章首先删除缺失率大于50%的指标，即删除“孩子个数”这个微观指标，将剩余指标赋值。文章用Y表示样本是否违约，当Y为1时表示样本违约，Y为0则表示样本未违约。其他的微观指标参照银行业信用风险评估指标的量化标准赋值。性别上，女性赋值为0，男性赋值为1；婚姻状况中，未婚赋值为1，已婚赋值为2，离异赋值为3；学历上，博士赋值为1，硕士赋值为2，大专、本科赋值为3，高中赋值为4，初中及以下赋值为5；公司规模在1 000人以上赋值为1，500～1 000人赋值为2，300～500 人赋值为 3，200～300人赋值为4，100～200 人赋值为 5，50～100 人赋值为 6，10～50 人赋值为 7，0～10人赋值为 8；营业收入中，50 000元以上赋值为1，10 000元～50 000元赋值为2，5 000元～10 000元赋值为 3，1 000元 ～5 000元赋值为4，0～1 000元赋值为5；借款目的，按用途的违约率从高到低进行赋值。用于流动资产违约率最高（27.13%），赋值为5，其次是用于业务周转的14.29%的违约率，赋值为4，违约率为10.20%的固定资产用途赋值3，违约率为5.13%的扩大经营赋值为2，违约率最低的其他用途赋值1。点融网为企业的信用评级按A级为1，B级为2，C级为3，D级为4进行赋值。

对于宏观指标均为连续型变量，CPI、GDP、M1、财政支出、ECI、CCI、PMI 以及 CERCI均是月度数据。由于只能搜集到季度失业率数据，且该指标并未像GDP是一个累计型指标，且失业率的波动幅度不大，故直接取其平均值作为月度数据；行业状况是将三个银行的半年报数据汇总后，按其违约率从低到高进行排序，违约率最低的行业赋值为1，稍高的赋值为2，以此类推。

（二）缺失数据处理

对于离散型变量，如婚姻状况、性别等变量，数据缺失值较少，采用众数填补法用以修复；对于连续型变量，运用SAS软件，将连续型指标导入后，分别利用MCMC算法运行1次、5次和10次后比较连续型变量的均值和标准差，所得结果如表1所示。通过比较后发现填充10次后的样本标准差较填充1次、5次的样本小，填充效果较好，故选多重MCMC填充10后的样本填补，得到完整数据。

表1 MCMC算法在不同运行次数下的填补结果

（三）平衡样本

将填充后完整的数据样本分为训练集与测试集。其中，训练集中有120个违约样本和965个非违约样本构成，违约率仅为11.06%，样本具有不均衡的特点。由于样本涉及的数据量并不是很大，不能采用欠抽样方法。文章采取过采样中的SMOTE算法，在原有数据的基础上产生新的数据。样本均衡前后违约样本的数目达到965，使得违约样本数与未违约样本数的比例为1∶1，训练集成为均衡样本。

（四）因子指标提取

目前删除部分缺失数据的指标后还剩下26个指标。但由于每个指标重要性不同，提取比率均不相同，对于重要性较低的指标则予以删除。其中学历、其他平台借款以及月收入提取比率过低，故将该两项指标剔除，将剩余23个指标进行因子分析。为了考察样本数据是否适合做因子分析，需要先做一个KMO和Bartlett的球形度检验，具体结果如表2所示。

表2 KMO和Bartlett检验结果

从表 2可知，KMO值为 0.706，大于0.6；且Bartlett的球形度检验的显著性为0.000，小于0.05，所以这23个指标适合做主成分因子分析。

文章将主成分分析方法提取出来的因子用Kaiser标准化最大方差法旋转，在10次迭代后样本收敛。查看旋转后的成分矩阵，可知每个因子中比重较大的指标，相关结果如表3所示。

表3 旋转后的成分矩阵

从表3可知，因子1、因子2与因子6其主要的显著成分均是宏观指标，剩余因子的主要显著性成分为微观指标，所以第一个因子由CERCI、M1、GDP和CCI构成，称为经济基本面因子；第二个因子由URI、PMI和ECI组成，称为经济景气因子；第六个因子则为财政支出因子；而其他剩余的6个因子为微观因子，分别称其为借款特征因子、借款情况因子、相关资产因子、信用等级因子、企业状况因子和个人特征因子。

通过主成分因子分析的训练集样本可以得到每个因子对应值，而对于测试集样本，则应将表4中的成分得分系数矩阵与标准化的测试集数据按照公式（2）对应计算出每个因子对应值。

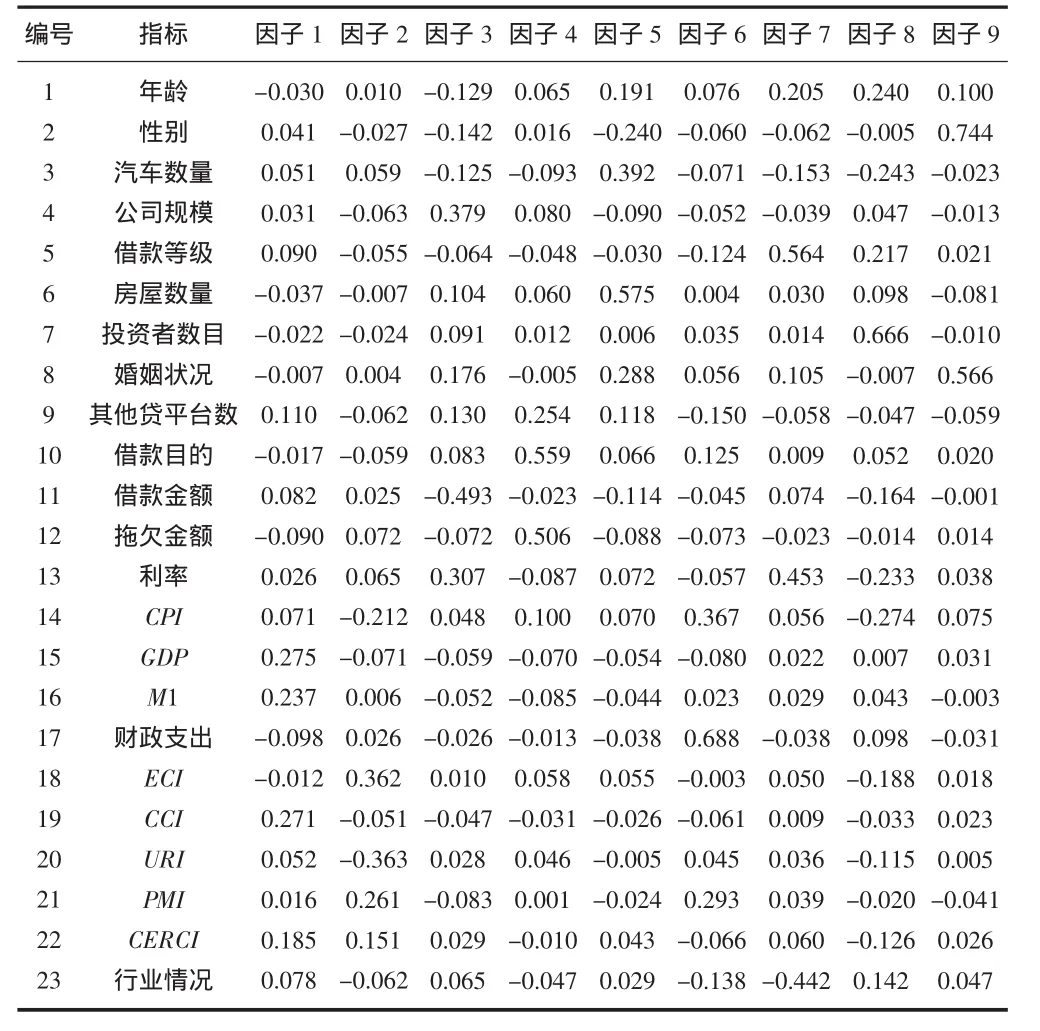
表4 成分得分系数矩阵

其中，i为每个因子编号数，i=1，2，3，…，9；Fi表示因子得分，xj表示每个样本对应指标的标准化值，aij表示为对应指标的系数值。

（五）信用风险评估结果

文章总共有2 230个样本进行实证，其中1 930组数据作为训练集得出神经网络模型，剩余300组数据作为测试集验证神经网络模型预测的精确度。多层感知器和径向基函数模型的输入层节点数由主成分因子分析得到的9个因子构成，即输入层有9个神经元，输出层节点数设定为1个。假设输出值接近于0时，为非违约企业；输出值接近于1时，为违约企业。在SPSS软件中输入相关因子，设定好相关程序后，得出输出结果。

1.多层感知器评估结果。根据软件要求及模型的需要，将模型体系结构中选择1层为隐藏层数，且隐藏层中最大单位数为50，选择调整的共轭梯度算法。将培训错误的最小相对变化设置为0.000 1，误差率最小变化设置为0.01。隐藏层激活函数采用双曲正切，而输出层激活函数采用Softmax。表5展示了测试集的预测结果。

表5 多层感知器的预测结果

从表5可知，多层感知器模型预测违约企业的精确度远高于预测非违约企业的精确度。从测试集的样本预测结果可知，非违约企业“0”判断的正确率为76.30%，但是对于违约企业“1”预测能力高，达到100.00%，整体预测正确率为79.00%。

2.径向基函数的结果。根据软件要求及模型的需要，隐藏层激活函数选择标准化径向基函数，且自动计算允许的重叠数量。表6展示了测试集的预测结果。

表6 径向基函数的预测结果

从表6可知，径向基函数模型无论预测非违约企业还是预测违约企业，其精确度均较高。从测试集的样本预测可知，非违约企业“0”判断的正确率为92.50%，对于违约企业“1”预测能力较高，达到97.10%，整体预测正确率为93.00%。

比较多层感知器与径向基函数神经网络的预测结果后发现，虽然在预测违约企业上，径向基函数与多层感知器的预测精确度均较高，但是多层感知器在预测违约企业上的优势较为明显。而在预测非违约企业上，多层感知器的精确度仅76.30%，但是径向基函数的预测精确度达到92.50%，优势明显。从总体预测精确度来看，径向基函数预测准确率为93.00%，高于多层感知器79.00%预测准确度，径向基函数的预测能力较强。

五、结论

文章首先根据点融网上中小企业的数据以及影响企业信用风险的宏观指标，建立了一套中小企业信用风险评估体系。利用Python技术获得点融网上关于中小企业信用贷款的1 392组数据，将缺失借贷时间的数据删除，填补完缺失数据后，利用SMOTE算法对训练集的样本平衡数据，从而获取的样本总数为2 230组。将1 930组训练集数据进行主成分因子分析，并将得到的因子与测试集的因子使用SPSS系统进行神经网络算法分类。

实证结果发现，在预测违约企业上多层感知器的预测正确率高于径向基函数，但在预测非违约企业的能力上径向基函数预测正确率略高，而径向基函数的总体预测能力较强。

从该实证结果可知，在众多指标中，因子1、因子2与因子6中比重较大的宏观指标对于中小企业的信用影响较大，也就是 CERCI、M1、GDP、CCI、URI、PMI、ECI与财政支出这些宏观指标较为重要；而剩余因子中比重较大的微观指标对于研究中小企业的信用风险研究也是较为重要的，如公司规模、借款金额、在点融的拖欠金额、借款目的、汽车数量、房屋数量、借款等级、投资者数目、性别和婚姻状况等指标在中小企业信用风险中评估中有十分重要的作用，故而应该将这些指标纳入中小企业信用评估指标体系中。

尽管文章使用的是P2P网络借贷平台的中小企业的借贷数据来研究中小企业的信用风险评估问题，但评估的方法与评估指标、评估结果均适用于一般的中小企业信用风险评估，对一般的中小企业信用风险评估时评估指标体系和方法的选择有一定的借鉴意义。