我国省级全要素生产率研究——基于Global Malmquist 指数的再测算

陈向武

（北京大学经济学院，北京，100871）

一、引言

常见的全要素生产率概念来自Solow（1956）的研究，他认为投入要素的增长不足以解释经济体之间的产出差距，并把产出增长率扣除要素增长率后的余值解释为技术进步率，这一余值被称为“Solow余值”，也就是Total Factor Productivity（简称TFP），而这一方法也成为计算TFP的重要方法之一。除此之外，许多学者又发展出随机前沿函数方法（Stochastic Frontier Analysis，SFA）、数据包络方法（Data Envelopment Analysis，DEA）等方法，成为TFP测度的重要方法。围绕我国改革开放以来近四十年的高速经济增长，学界涌现出不少测算和探讨我国经济增长源泉的文献，但是由于对要素投入和测算方法的不同理解，学界对TFP在我国经济增长中的作用并未达成一致性认识，甚至出现了方向相反的结论。目前国内学者最常用的研究测算我国TFP的是基于Solow模型的增长核算法与基于DEA的Malmquist TFP指数法。无论是哪种测算方法，在具体测算过程中都需要以一定的理论假设为前提，并以此为基础，建立测算模型来实现。因此理论假设是否更契合于客观现实，将决定测算结果是否能更准确地反映真实状态。如下，本文通过对既有研究成果的回顾与分析发现，相比于增长核算法，非参分析中的DEA Malmquist 方法测算TFP更具有优势，但同时也需要在测算模型与投入要素的度量方面作出改进。

二、文献综述

国内学者基于增长核算法对我国TFP变动进行了研究，但是研究的结论却不尽相同：一些研究认为我国的TFP的贡献较小，经济增长主要由要素投入推动（孙琳琳和任若恩，2005；郭庆旺和贾俊雪，2005），持相反结论的研究则认为我国经济增长TFP改进明显（张军和施少华，2003；王小鲁等，2009）；一些研究认为我国东部地区TFP低于西部，TFP呈现收敛（叶裕民，2002），相反的研究结论则认为经济发达地区TFP显著高于落后地区（李静等，2006）。对不同研究差异可以从两个方面进行解释：一是要素度量的误差，这是所有测算TFP方法都共同面对的问题，Jorgenson 和Griliches（1967）早就指出TFP可能是要素度量误差的表现，而大部分基于增长核算法测算TFP的研究都未将人力资本作为投入要素加以考虑，而包含人力资本作为投入要素的研究则常常因为选择不尽一致的人力资本代理变量，而使得研究结果也不相同（章祥荪和贵斌武，2008）；二是模型参数设置估算的问题，增长核算法测算TFP的研究的首要问题是估算要素的产出弹性，一个方便可行的方法是假设要素产出弹性在TFP的测算期间不变，以此利用收入弹性法或者建立计量模型进行估算。叶裕民（2002）、彭国华（2005）的研究中都假设了所有省份要素产出弹性相同，且不随时间变化，由于我国经济发展水平地区悬殊，假设所有省份要素产出弹性相同不尽合理。对于发达经济体，产业结构、要素投入比率都相对稳定、成熟，假设产出弹性在TFP测算期间为常数有其合理性，但我国历史原因造成的要素市场资本流动性受限（张吉鹏和吴桂英，2004），经济仍处于二元经济结构到新古典转变过程中的现状（蔡昉，2013），显然是不符合要素产出弹性不随时间变动的假设的。要素产出弹性是时间的函数，生产要素投入的改变会引起其产出弹性的进一步改变（陈瑾瑜，2012），将要素产出弹性设为常数用于估计TFP很可能是有偏的甚至有误的（章上峰和许冰，2009）。

非参分析中的DEA Malmquist TFP指数测算我国省级TFP有其特殊意义，该方法只需要经济系统的要素投入、产出数据，而不需要对生产函数及其参数有任何假设，就可以通过线性规划求解而得到TFP。国内有许多学者基于该指数方法对我国全要素进行了测算，但对于我国整体及地区间TFP的具体变动却存在差异，有些结论甚至相矛盾。一些研究通过测算发现我国TFP整体存在改进（颜鹏飞和王兵，2004；孟令杰和李静，2004；郑京海和胡鞍钢，2005；金相郁，2007；魏梅，2008；于洁等，2009；王欣亮和严汉平，2014），持相反的意见的研究则发现我国TFP整体负增长，我国经济增长仍主要依靠要素投入来拉动（郭庆旺等，2005；何元庆，2007；董丽霞，2010；刘建国等，2012；张自然和陆明涛，2013）；一些研究认为我国TFP的改善主要源于技术进步（孟令杰和李静，2004；何元庆，2007；傅勇和白龙，2009），相反的观点则认为我国TFP的改进是技术效率改善带来的（颜鹏飞和王兵， 2004）；一些研究发现我国东部发达地区的TFP高于西部落后地区（孟令杰和李静，2004；郭庆旺等，2005；金相郁，2007；魏梅，2008；董丽霞，2010；刘建国等，2012），另外的一些研究则认为西部地区的TFP高于东部地区，呈现地区收敛趋势（颜鹏飞和王兵，2004；陈诚，2010）。

章祥荪和贵斌武（2008）对上述研究结论差异给出了部分解释，其认为国内学者TFP的测算结果不一致较多是由于资本存量数据差异（期初资本，价格指数，折旧率等选取不同）导致的，通过测算发现1978-2005年我国TFP增长主要源于技术进步，且东部明显，地区差异加大。本文认为以上TFP测算研究其结论不一致仍可以归结为两大原因：一是投入要素的度量，即资本存量数据差异（章祥荪和贵斌武，2008）及对人力资本这一投入要素变量的处理上，既有DEA Malmquist指数测算TFP的研究绝大多数都未将人力资本纳入考虑，岳书敬和刘朝明（2006）引入了教育年限为代理变量的人力资本，发现在引入人力资本要素后,1996—2003年区域TFP的增长得益于技术进步;如果不考虑人力资本存量,则低估了同期的技术效率提高程度,而高估了期间的技术进步指数；另一重要原因在于，对于模型设定上，既有研究普遍采用Fare等（1994）定义分解的Malmquist TFP指数，该指数存在局限性，如相邻两期的指数测算的结果通常不一致，因此需要取几何平均值，通过线性规划求解可能不可行，求得的TFP的结果不具有乘法完备性（Pastor和Lovell，2005），而这些可能造成不同研究所得到的结论不一致。

本文拟从两个方面对现有的DEA Malmquist指数测算我国省级TFP的研究做出改进，并以此对我国省级层面TFP的变动情况进行测算。首先从要素投入角度，将投入要素界定为人力资本、实物资本、劳动投入，即通过引入人力资本作为投入要素，且人力资本的度量选择与实物资本相一致的永续盘存法；进一步的，引入Pastor 和 Lovell（2005）定义的Global Malmquist TFP指数，可以克服传统Malmquist TFP的重要缺陷，使测算结果更具有稳健与准确性。

三、 测算模型

Charnes等（1978）引入了评价决策单元效率的数据包络分析法（第一个DEA模型CCR），该方法后来被广泛应用于效率测算，TFP测算即是该方法的应用。传统的投入角度的CCR模型描述如下：

解式（2），若θ值的最优解θ*＝1，则待评价单元的投入产出是DEA有效的，若θ*＜1则说明待评价单元为DEA无效。θ*的经济学含义在于，通过投入产出DEA有效单元的线性组合，可以将待评价单元的投入缩小至原投入的θ*倍，而不降低其产出。

该方法后来被广泛应用于效率测算，TFP测算即是该方法的应用。用DEA测算TFP主要是基于Malmquist指数，该指数源自Malmquist（1953）对不同时期消费变化的研究。具体而言，要计算Malmquist生产率指数，就要定义距离函数。设定生产集为：

则投入角度的距离函数为：

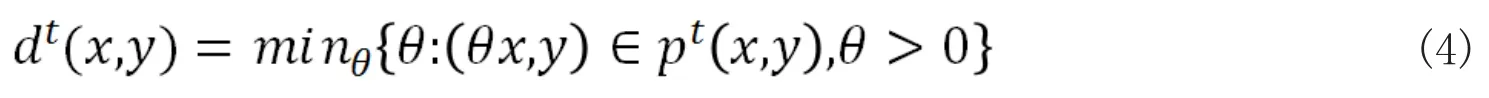
考虑t期为基期，可以定义投入生产率指数为

考虑t+1期为基期，可以定义投入生产率指数为

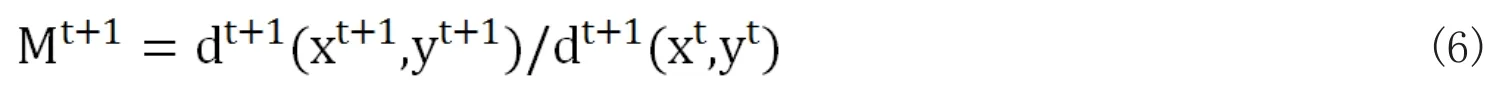
Fare等（1994）利用两期指数的几何平均来定义传统Malmquist TFP指数并进一步分解,则投入角度的Malmquist TFP指数如下：

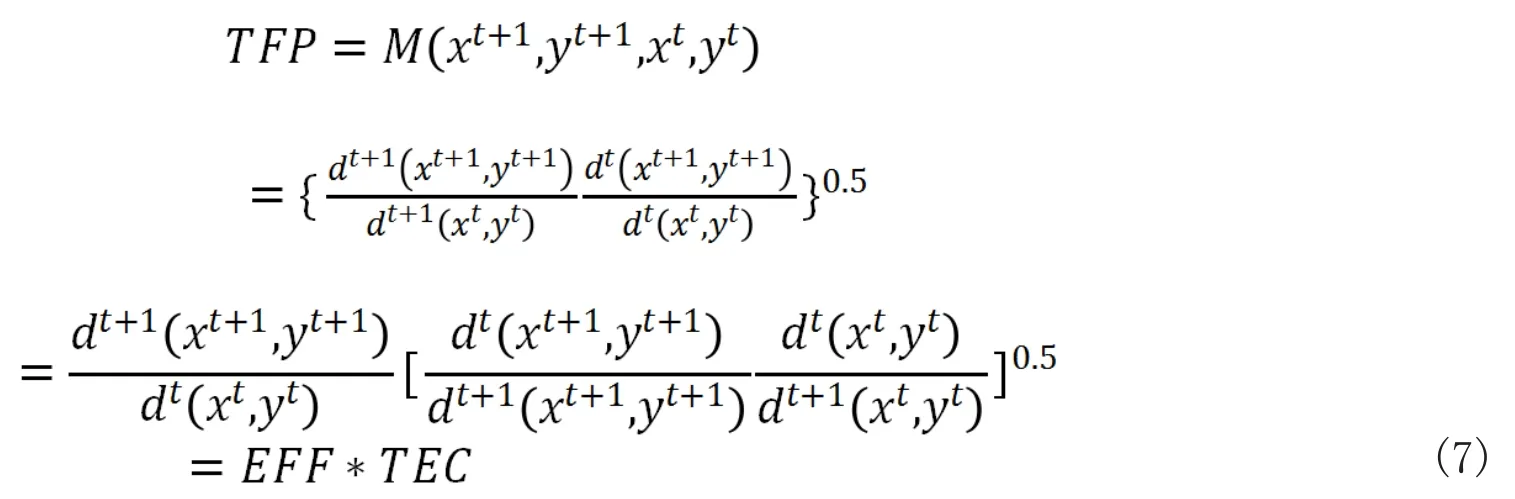
(7)式中，TEP指数最后分解为两项，第一项EFF为规模报酬不变假设下的技术效率变化，此项可进一步分解为纯技术效率和规模效率；第二项TEC为规模报酬可变假设下的技术进步率。

需要强调的是，DEA方法测算的技术变动都是基于各生产前沿面的相对变动，而不是绝对技术变动。Ray 和 Desli（1997）认为以上该指数分解存在缺陷，即如果技术前沿是规模报酬不变，技术进步率的计算没有问题，但是此时不存在规模效率；而如果技术前沿规模报酬可变，则技术进步率不能反映给定投入约束下最大产出如何随技术变动，其认为应该通过引入固定基期，利用技术前沿规模报酬可变假设，重新分解Malquist TFP指数。Pastor和Lovell（2005）提出该指数存在三大缺陷：包括MT、MT+1计算的结果通常不一致（因此需要对指数取几何平均值）；通过线性规划求解可能不可行；求得的结果不具有乘法完备性1，其提出如下改进。

通过构造Global Malmquist 指数，定义生产集：

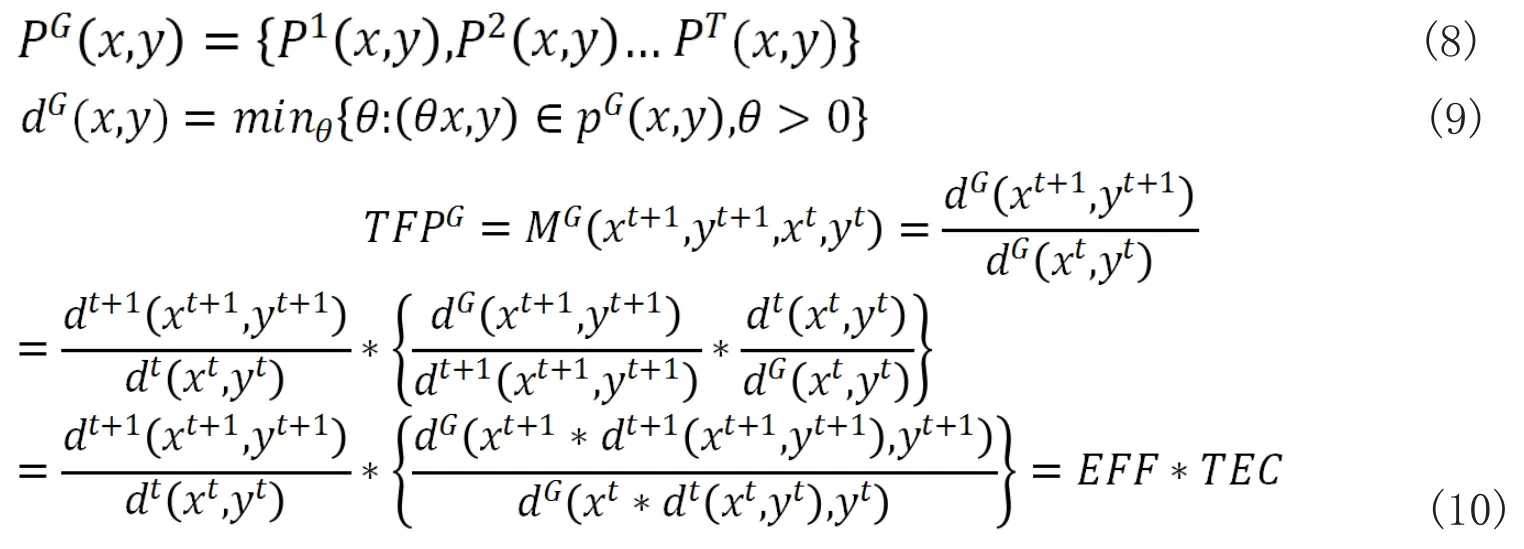
以上Global Malmquist指数具有乘法完备性、不会因为基期设置不同而造成测算结果差异、且不会产生线性规划不可解等问题（Pastor和Lovell，2005；夏一丹等，2014）。杜江（2015）、康海媛等（2016）分别利用该方法分别测算了我国省级农业和能源TFP。

本文拟采用Pastor和Lovell（2005）定义、分解的Global Malmquist指数，对我国省级TFP进行测算。测算思路为，通过求解四个距离函数，进一步将TFP分解为技术效率改进(EFF)、技术进步(TEC)。

距离函数问题转化为常见的线性规划问题，可以利用常用的数学软件（如Matlab）代入投入产出数据求解以上问题。

四、全要素生产率的测算及结果

（一）投入和产出变量界定

投入变量界定为实物资本、人力资本、劳动力（各地劳动年龄人口扣除高中以上在校生人数得到），产出界定为地区生产总值（利用当年GDP平减指数扣除价格影响）。以下具体说明关键变量实物资本与人力资本的构造与测算数据来源。

实物资本采用永续盘存法测算：

式（12）中，Kit为第i省在第t年末的实物资本存量，δit为第i省在第t年的折旧率，Iit、Pit分别为第i省在第t年的固定资产资本投资流量及对应价格指数。由《中国统计年鉴》取得历年地区固定资产投资、固定资产投资价格指数数据，各省、市折旧率采用贾润崧和张四灿（2014）测算结果，通过假设期初两期物质资本与产出比不变来确定期初资本存量，由此得到各地区历年物质资本存量。

人力资本同样采用基于成本法的永续盘存法：

δit为第i省在第t年的折旧率，Tit为第i省在第t年的人力资本平均使用年限，则折旧率的确定进一步转化为人力资本平均使用年限Tit的确定。

人力资本存量的确定转化为对人力资本投资流量、价格指数及期初资本存量的确定。人力资本的投资流量由省级人力资本教育经费支出与卫生总费用组成；价格指数为固定资产投资价格指数与地区居民消费价格指数加权平均数；通过假设期初两期人力资本与产出比不变来确定期初人力资本存量。考虑人力资本的流动会导致人力资本存量在空间布局的变动，引入省际人力资本净流入netit，netit反应的是第i省在第t年的人力资本净流入量,通过所有人口净流出省份上年平均人力资本乘以人口净流出再加总，可以得到整体的人力资本净流出，再对应的人口净流入省份的人口净流入数据，测算得到netit。

中间变量在测算过程中，所需的数据来源如下。由《中国统计年鉴》获取的数据：地区生产总值，地区人均可支配收入，地区居民消费价格指数，地区固定资产投资价格指数，地区人口年龄结构组成，地区公共财政预算关于教育、医疗的支出，地区城镇、农村居民教育、医疗平均消费支出，各地区在校学生数、地区居民平均寿命。由《中国人口和就业统计年鉴》获取的数据：地区人口年末数2《中国人口和就业统计年鉴1996》给出的人口数定义为一定时点、一定地区范围内有生命的个人总和。，地区人口自然增长率，地区城镇人口比率，各地区农业人口比例由《中国教育经费统计年鉴》获取的数据：地区教育经费总支出、学杂费。由《中国卫生和计划生育统计年鉴》获取的数据：地区卫生总费用、全国卫生总费用。个别缺失数据，通过插值法估算得到。

（二）测算结果

本文测算了1996-2013年间我国31个省、市3受限于成本法度量人力资本相关数据来源的局限性，即1996年前相关投资数据缺失或者不完备，2014年及以后相关统计年鉴尚未公开发行，本文的研究区间界定为1996-2013年间；重庆市于1997年设为直辖市，本文对其1996年包括资本存量、生产总值数据做了处理，与四川省并立。TFP变动情况，为了方便分析比较，本文构建了三个模型，模型一和模型二为Pastor 和 Lovell（2005）定义的Global Malmquist TFP（记为TFPGM指数，其中模型一投入要素包含人力资本，模型二不包含人力资本，模型三为Fare 等（1994）定义的Malmquist TFP（记为TFPM），投入要素包含人力资本。

1.生产技术前沿变动

DEA最初的运用是基于可比性决策单元的投入、产出数据，利用线性规划模型，构造生产技术前沿分析决策单元有效性，因此在正式测算TFP之前，利用DEA方法可以简单评估1996-2013年间构成31个省、市生产技术前沿的省份变动情况，将每年31个省、市的投入、产出数据分别带入线性规划模型，可以求得每一个省份当年对应的效率系数(0＜θ≤1)，θ值越大表明生产越有效率，θ＝1的省、市为处于生产前沿省份。为方便对比，本文测算了包含人力资本与不包含人力资本作为投入要素的效率系数，分别记为θH、θN。

测算结果显示（见附件1）：首先，整体上看，对于同一个省、市在相同年份，θH≥θN普遍成立，即考虑人力资本测得的效率系数大于不考虑人力资本作为投入要素的效率系数；这也印证了，随着我国经济发展，人力资本越来越成为一种重要的投入要素变量，因此将人力资本作为投入要素代入TFP测算的是合理与必要的；其次，由包含人力资本作为投入要素测算得到的效率系数值看，广东、上海、山东一直处于生产技术前沿（θH＝1），而北京、天津、内蒙古由于近些年的持续效率改进，也渐渐回升至生产技术前沿，但内蒙古、山东包含人力资本与不包含人力资本作为投入要素的效率系数近些年出现严重背离，而处于生产前沿的其他省、市这两项指标比较吻合；最后，由效率系数值的分布来看，我国绝大多数省、市的生产效率仍然比较低下，地区效率差距巨大。投入型DEA测算的θH的经济学含义在于，如果可以利用处于生产技术前沿的省、市的技术，通过线性组合，那么可以实现将目标省份的投入降至θH，而不至于降低其产出。以2013年全国效率系数最低的西藏自治区为例，θH＝0.41，意味着利用2013年处于生产前沿的北京、天津、内蒙古、上海、江苏、山东、广东的技术，通过这七个省、市的投入、产出数据，就可以得到一个产出与西藏当年水平一致，但投入却只有西藏当年实际要素投入41%的水平的线性组合。

基于以上分析，本文得出如下结论。

第一，我国省级投入产出效率整体水平较低，人力资本是影响地区投入产出效率的关键因素。2013年31个省、市包含人力资本的投入产出效率算数平均值为0.78，大部分地区的投入产区效率介于0.6与0.8之间，反映了投入产出效率低下导致的要素投入浪费严重，不包含人力资本的投入产出效率算数平均值仅为0.63，显示了人力资本作为投入要素对产出效率的提升作用；

第二，横向不同地区的比较来看，投入产出效率地区差异明显。东部发达地区显著高于中、西部，投入产出效率与人均GDP之间的具有强相关性，人均GDP越高的地方，投入产出效率越高，对于落后地区而言，提升投入产出效率有其重要意义（见图1）；

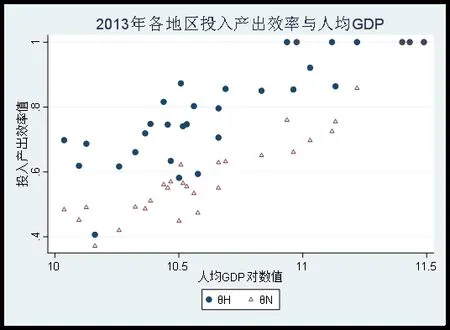
图1 2013年各省市投入产出效率与人均GDP

第三，纵向随时间变动的趋势来分析，我国省级投入产出效率改善程度较小。1996-2013年间。我国省级投入产出整体变化不大，具体到东部地区存在一定程度的效率改善，但是中、西部省份投入产出效率基本不变，甚至个别省份出现效率恶化，技术落后地区没有表现出更快的效率改善。

2．全国TFP变动情况4DEA方法基于面板分析，理论上得到的只是各省、市TFP数据，全国TFP数据，采用当年31个省、市几何均值，因此此TFP数据并不真实反应全国整体的TFP变动。（见附件2）

总体上，模型一、二、三得出的我国1996-2013整体的TFP增长率均值分别为-0.74%、-0.94%、-1.17%。对比模型一、三，发现TFPGM1下降速度显著小于TFPM，由于技术效率项的分解都是基于不变规模报酬假设，因此EFFGM1与EFFM测算结果一致，技术进步项TECGM1、TECM估计的不同造成了TFPGM1、TFPM差异，反映了不同的TFP指数构造方法，是导致测算结果不一致的原因；相比模型一、二，尽管TFPGM1、TFPGM差异不大，但是TECGM1增长率为-0.72%，TECGM2增长率为0.33%，即包含人力资本模型的结果为技术进步率为负，而不含人力资本模型的结果为技术进步贡献率为正，反映了人力资本投资在我国生产中起着越来越重要的作用，如果忽视人力资本这一重要投入要素，必然会导致TFP测度结果出现较大误差。以上结果验证了本文之前的推断，即不同的Malmquist指数构造及分解方法和人力资本作为投入要素的引入，会导致基于DEA方法研究TFP的结论不一致。

回到模型一，1996-2013年间，我国TFP变动经历了三个阶段，第一阶段是1996-2004年间，TFP经历了持续下滑，可能的原因在于，20世纪90年代初期，我国整体宏观经济出现“滞涨”，投资过热、产能过剩，同时国有企业改革启动，带来劳动力的暂时失业等造成了TFP的恶化（张自然和陆明涛，2013）；2004-2011年间TFP持续回升，则得益于加入世贸组织以后，为我国提供了更广阔的产品、技术市场（何元庆等，2007），我国快速融入全球分工格局（张自然和陆明涛，2013），伴随着经济体制变革下的市场化改革、城市化推进、大规模的基础设施投入等（郭庆旺和贾俊雪，2005；王小鲁等，2009）都促进了TFP的持续提升；2011-2013年间TFP又重回下降通道的可能解释是，2008年全球性金融危机后，大规模的财政、货币政策刺激，虽然避免了短期内经济的下滑，但是政府主导的投资，进一步恶化了经济结构问题，使得本该淘汰的落后产能得以延续，造成了TFP的持续下滑（刘金贺，2012）。

3．各地1996-2013年间平均变动情况（见附件3）

分别比较模型一、三和模型一、二，仍然可以发现即不同的Malmquist指数构造及分解方法和人力资本作为投入要素的引入，会导致基于DEA方法研究TFP的结论不一致。回到模型一，区别于全国整体情况，1996-2013年间东部地区由于技术效率改进（年均增长0.19%），TFP水平得到微小改善（年均增长0.01%）；同样西部地区由于技术效率改进（年均增长0.22%），其TFP的下降速度小于中部（年均增长-0.74%）；中部地区TFP增长率为-1.68%。由以上分析可见，从地区分布上看，我国TFP东部地区优于西部地区，而中部地区反而最弱，这点与傅勇和白龙（2009）的结论相一致，可供的解释是东部地区有先天的对外开放优势，而西部地区有政策支持，即西部大开发的系列政策为西部地区的技术效率改进创造了条件（刘生龙等，2009），而中部地区却显得相对薄弱。制度变革在技术不变的情况下，提高了生产效率，因此东部、西部技术效率的持续改善，反映了经济体制改革得以深化，但是技术进步缓慢使得TFP增长缓慢甚至负增长（颜鹏飞和王兵，2004）。以此进一步反映了我国经济增长的自主创新动力不足，TFP的改善仍主要依靠经济体制改革带动技术效率的改进得以实现。

4．东、中、西部地区区间TFP变动情况（见附件4）

1996-2004年间，全国、东、中、西部TFP增长率年均分别-1.54%、-0.32%、-2.16%、-2.42%，东部地区由于技术效率进步年均0.17%，使得其TFP下滑速度低于全国水平，中、西部TFP即其组成成分变动相对一致；2004-2011期间，全国、东、中、西部TFP增长率年均分别0.62%、0.76%、-0.26%、1.27%，全国层面TFP改进的主要贡献源于技术效率的改进，对于东部地区则主要是技术进步（年均增长0.53%）贡献了TFP的增长，西部地区则是由于技术效率的显著改善提升了TFP水平；2011-2013期间，全国、东、中、西部TFP增长率年均分别-2.29%、-1.26%、-4.66%、-1.36%，整体与地区的趋势一致，技术效率微小改进，但是技术进步大幅下滑。

由以上分析我们发现，东部地区在TFP变动的三个时间区间里技术效率改进都显著为正，反映了东部地区作为我国经济体制改革、对外开放的最前沿，受益于既有的改革开放成果及持续的改革红利，技术效率得以持续改进；同时由于我国完成包括国有企业改革等一系列市场化的经济体制改革及加入世贸组织后的发展机遇，东部地区在2004-2011年间经历了技术进步的快速提升，同时行政性垄断，重复建设等非市场化制度可能是东部地区TFP提高难以持续提升的原因（楚尔鸣和马永军，2013）。

五、 总结

本文基于DEA Malmquist指数方法测算我国省级TFP变动，通过选用Pastor和 Lovell（2005）定义的Global Malmquist指数，区别于传统研究经常采用的Fare等（1994）定义分解的Malmquist TFP指数，同时将人力资本存量作为投入变量，发现不同的Malmquist指数构造及分解方法和人力资本作为投入要素的引入，使得TFP测算结果不一致，这或许能部分解释目前基于DEA方法对TFP的研究中，结论不一致的原因。基于DEA测算结果，总结如下：

首先，我国省级投入产出效率整体水平较低。人力资本是影响不同地区投入产出效率的关键因素，这或许可以为落后地区提升经济效率提供一个人力资本的解决方案；地区分布上，投入产出效率差异明显，东部发达地区显著高于中、西部，投入产出效率与人均GDP之间的具有强相关性，人均GDP越高的地方，投入产出效率越高，对于落后地区而言，提升投入产出效率有其重要意义；动态上看，我国省级投入产出效率整体变化不大，具体到东部地区存在一定程度的效率改善，但是中、西部省份投入产出效率基本不变，甚至个别省份出现效率恶化，技术落后地区没有表现出更快的效率改善。

其次，1996-2013年间我国整体TFP水平改善有限，尽管经济体制改革和对外开放等带来的技术效率改进明显，但是技术进步有限制约了TFP水平的提升。地区分布来看，东部、西部由于技术效率改进，东部还伴随着技术进步，使得TFP水平呈现东、西、中部从高到低排列。具体地，由于我国宏观经济政策对“滞涨”、投资过热、产能过剩的调整及国有企业面临的经营困境，造就了1996-2004年间，我国TFP的持续下滑；而之后，得益于我国加入世界贸易组织，包括国有企业改革等一系列市场化的改革措施，我国整体TFP经历了2005-2011年的持续改善；再往后，为应对2008年全球性金融危机的大规模财政刺激政策所导致经济结构负面影响，使得2011年开始TFP重回下滑通道。我国TFP的改进主要源于技术效率的改进。而技术效率改进通常被认为是经济体制改革、对外开放及一系列市场化手段的成果；而行政性垄断，重复建设等非市场化制度则可能进一步恶化技术效率。

最后，从TFP的结构变动上看，技术进步仍未成为我国TFP改善的主要因素，以此反映了我国经济增长的自主创新动力不足。

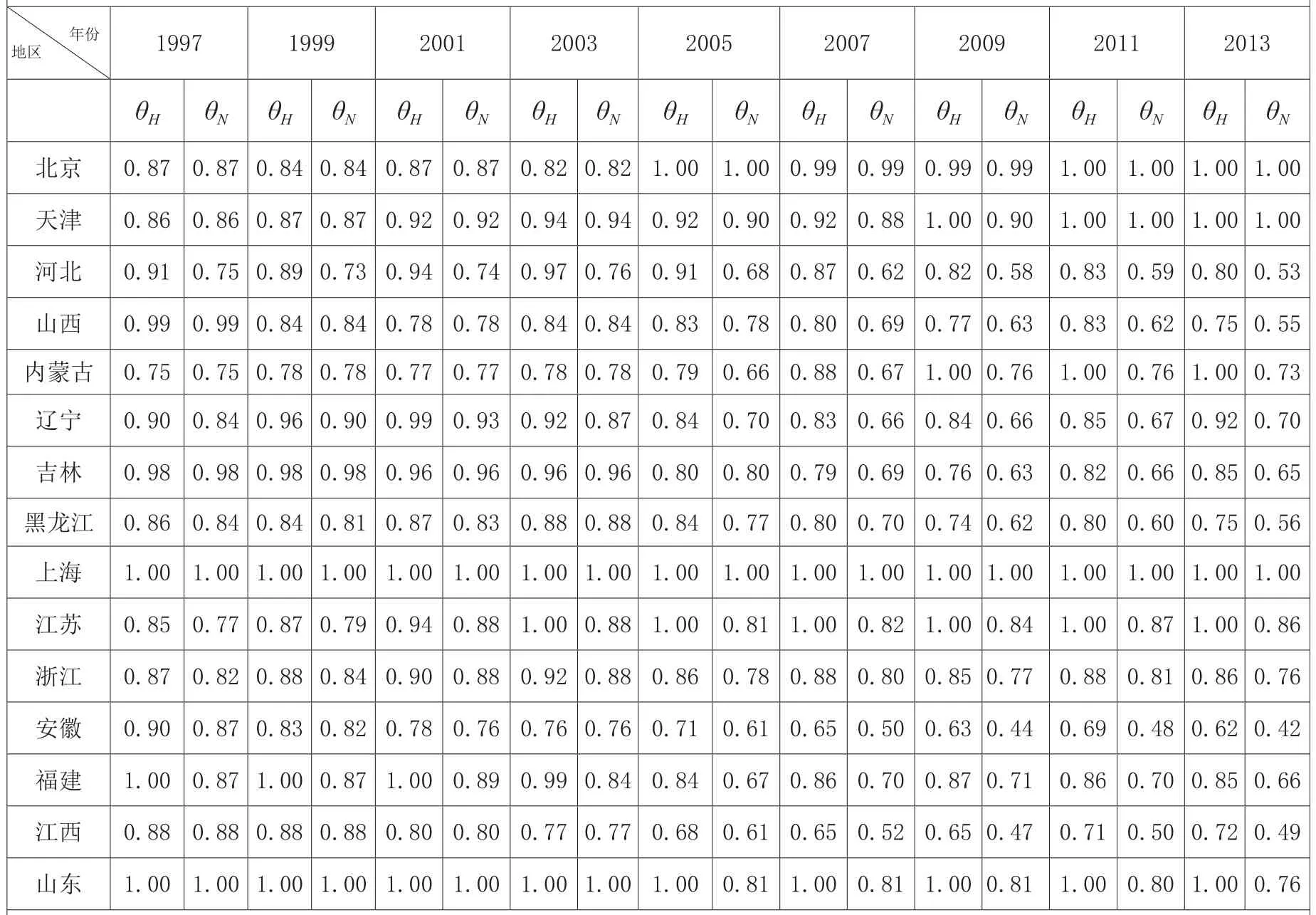
附件1 DEA测算的1996年-2013年我国各省、市效率系数表(θHθN)为便于比较，只报告奇数年

续附件1 DEA测算的1996年-2013年我国各省、市效率系数表(θHθN)为便于比较，只报告奇数年

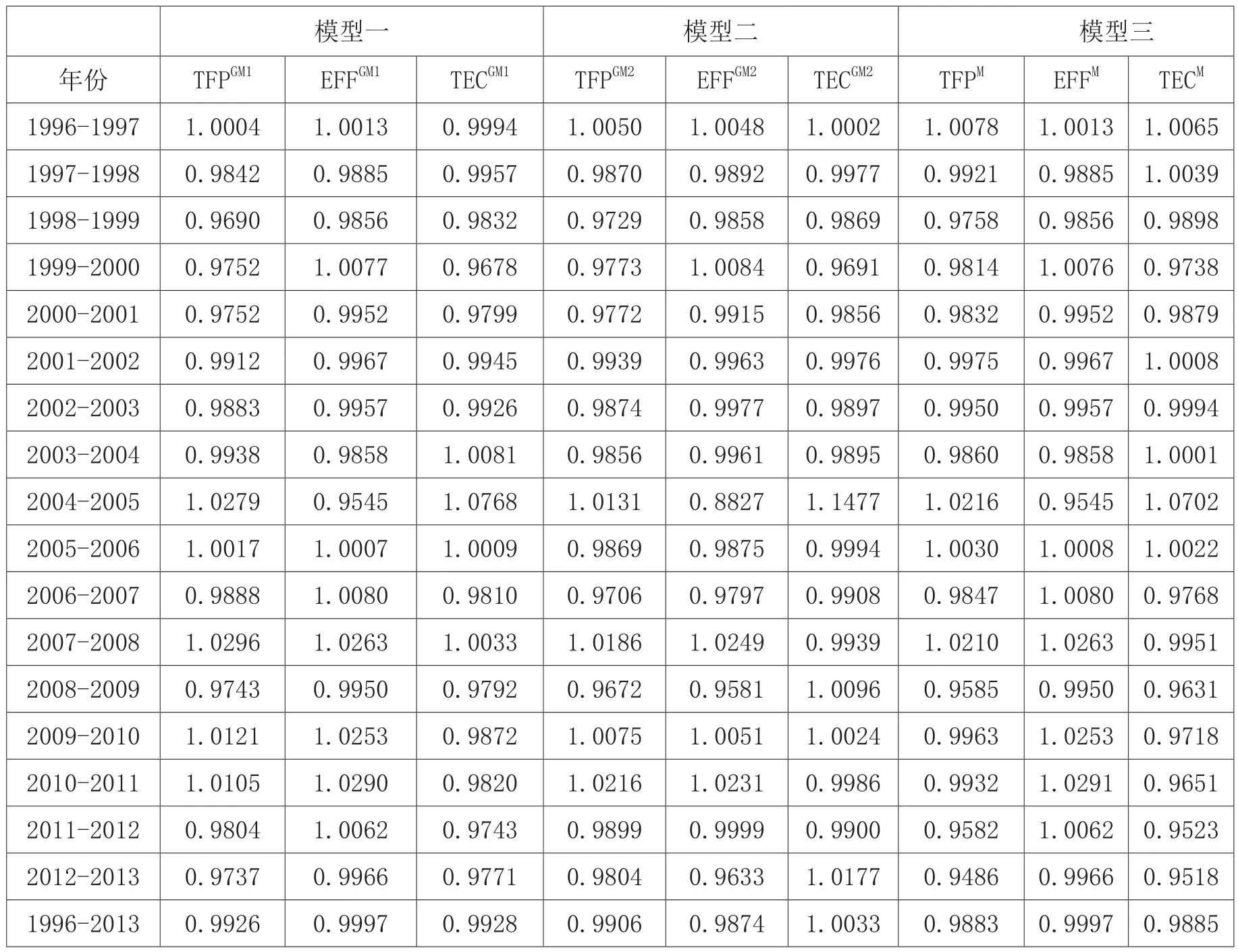
附件2 由省级平均的全国全要素生产率

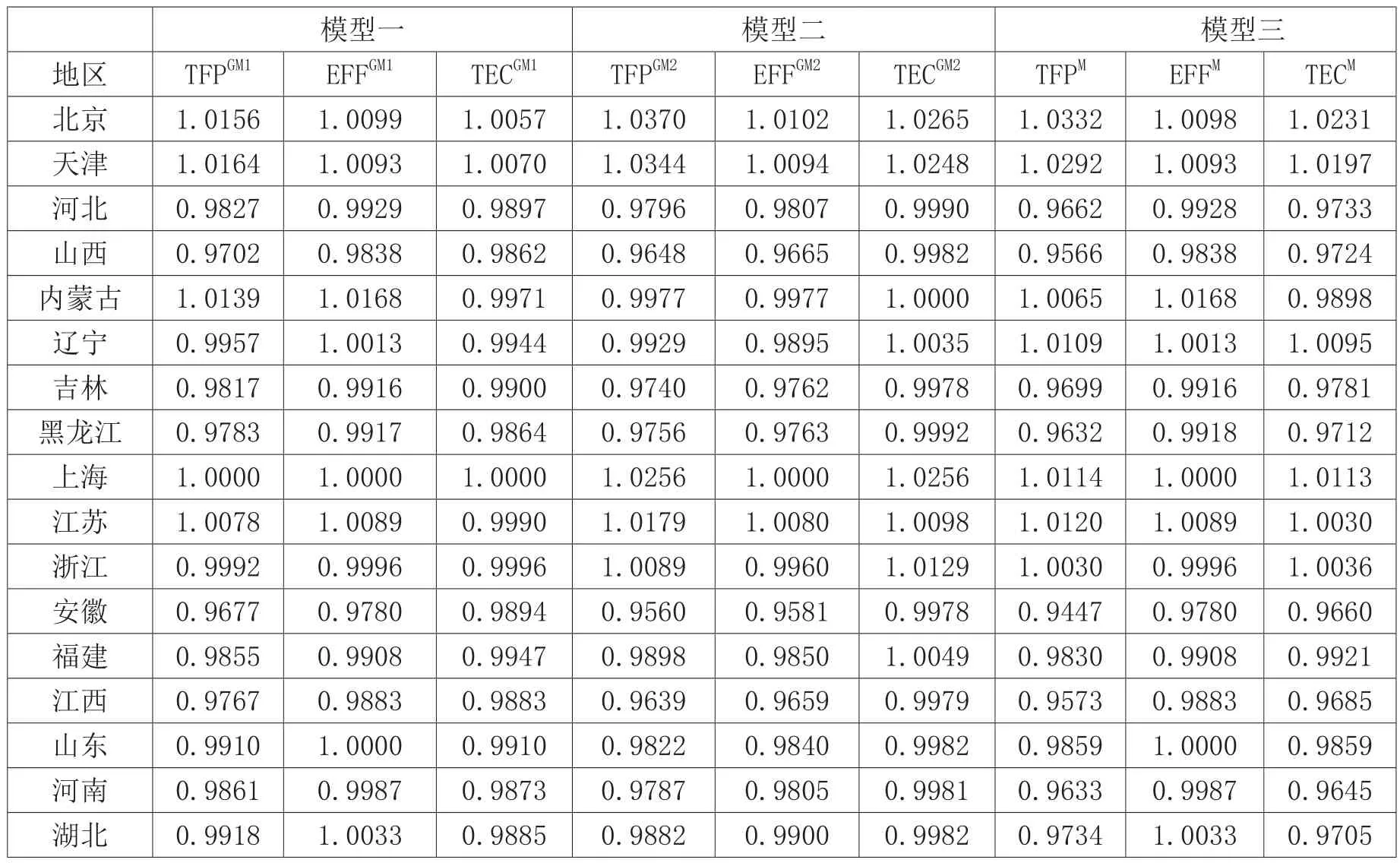
附件3 各地1996-2013年间全要素生产率年均值

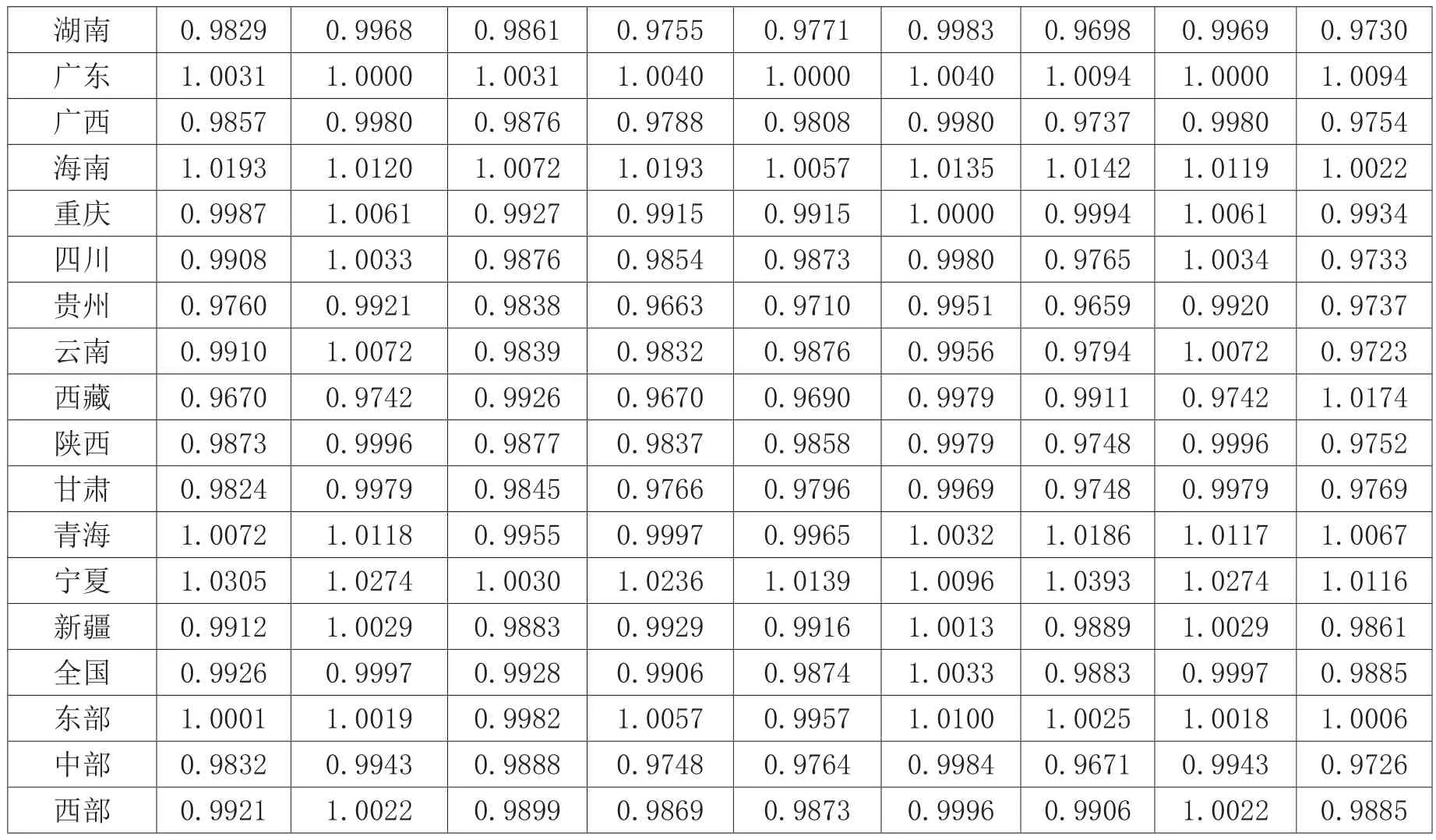
湖南 0.9829 0.9968 0.9861 0.9755 0.9771 0.9983 0.9698 0.9969 0.9730广东 1.0031 1.0000 1.0031 1.0040 1.0000 1.0040 1.0094 1.0000 1.0094广西 0.9857 0.9980 0.9876 0.9788 0.9808 0.9980 0.9737 0.9980 0.9754海南 1.0193 1.0120 1.0072 1.0193 1.0057 1.0135 1.0142 1.0119 1.0022重庆 0.9987 1.0061 0.9927 0.9915 0.9915 1.0000 0.9994 1.0061 0.9934四川 0.9908 1.0033 0.9876 0.9854 0.9873 0.9980 0.9765 1.0034 0.9733贵州 0.9760 0.9921 0.9838 0.9663 0.9710 0.9951 0.9659 0.9920 0.9737云南 0.9910 1.0072 0.9839 0.9832 0.9876 0.9956 0.9794 1.0072 0.9723西藏 0.9670 0.9742 0.9926 0.9670 0.9690 0.9979 0.9911 0.9742 1.0174陕西 0.9873 0.9996 0.9877 0.9837 0.9858 0.9979 0.9748 0.9996 0.9752甘肃 0.9824 0.9979 0.9845 0.9766 0.9796 0.9969 0.9748 0.9979 0.9769青海 1.0072 1.0118 0.9955 0.9997 0.9965 1.0032 1.0186 1.0117 1.0067宁夏 1.0305 1.0274 1.0030 1.0236 1.0139 1.0096 1.0393 1.0274 1.0116新疆 0.9912 1.0029 0.9883 0.9929 0.9916 1.0013 0.9889 1.0029 0.9861全国 0.9926 0.9997 0.9928 0.9906 0.9874 1.0033 0.9883 0.9997 0.9885东部 1.0001 1.0019 0.9982 1.0057 0.9957 1.0100 1.0025 1.0018 1.0006中部 0.9832 0.9943 0.9888 0.9748 0.9764 0.9984 0.9671 0.9943 0.9726西部 0.9921 1.0022 0.9899 0.9869 0.9873 0.9996 0.9906 1.0022 0.9885

附件4 各地分时期全要素生产率年均值

贵州 0.9422 0.9629 0.9784 1.0089 1.0162 0.9928 1.0009 1.0276 0.9740云南 0.9871 1.0062 0.9810 0.9943 1.0016 0.9927 0.9947 1.0313 0.9645西藏 0.9397 0.9568 0.9821 0.9869 0.9708 1.0165 1.0095 1.0592 0.9531陕西 0.9690 0.9876 0.9812 1.0153 1.0126 1.0026 0.9647 1.0024 0.9625甘肃 0.9801 0.9996 0.9805 0.9928 0.9971 0.9957 0.9562 0.9938 0.9621青海 0.9816 0.9906 0.9909 1.0378 1.0357 1.0021 1.0053 1.0145 0.9910宁夏 1.0013 1.0012 1.0001 1.0723 1.0640 1.0078 1.0062 1.0082 0.9980新疆 0.9877 0.9879 0.9999 1.0042 1.0220 0.9826 0.9602 0.9974 0.9627全国 0.9846 0.9945 0.9900 1.0062 1.0053 1.0010 0.9771 1.0014 0.9757东部 0.9968 1.0017 0.9951 1.0076 1.0023 1.0053 0.9874 1.0012 0.9862中部 0.9784 0.9925 0.9857 0.9974 0.9986 0.9988 0.9534 0.9863 0.9666西部 0.9758 0.9879 0.9878 1.0127 1.0149 0.9978 0.9864 1.0155 0.9714