核心素养视角下的绝对值不等式的复习策略

叶丹

（福州第四十中学，福建 福州 350007）

一、考点分析，明确绝对值不等式模块的复习方向

从福建卷到全国卷,理科数学的选考从矩阵与变换、坐标系与参数方程、不等式选讲中的三选二，前期是改为几何证明选讲、坐标系与参数方程、不等式选讲中的三选一，由于不等式选考常考察运用柯西不等式、均值定理证明不等式，因此在高三总复习中我校高三集备组统一采取回避不等式选考的方式。2017年全国卷选考调整为从坐标系与参数方程、不等式选讲中二选一，而且纵观近三年的全国卷的不等式选考的试题，考察知识点多为绝对值不等式的解法及运用。近三年全国卷的不等式选考的试题考察知识点统计如下：（见表1）

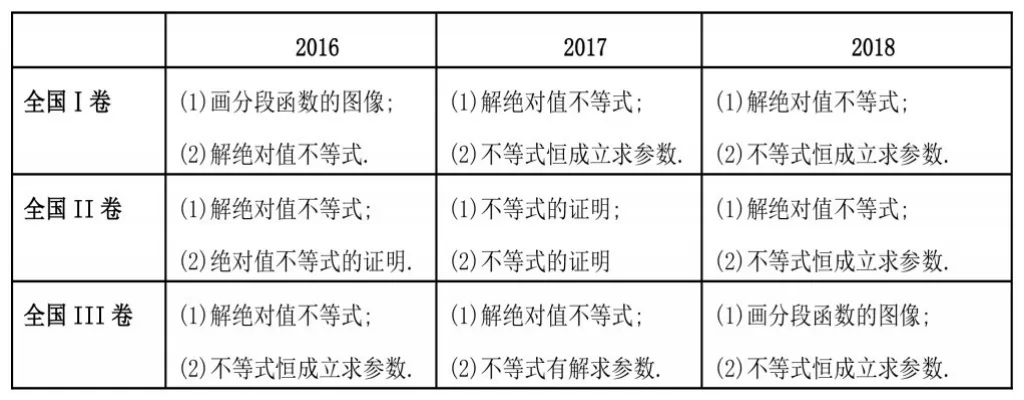
表1 近三年全国卷的不等式考点

针对以上统计结果，并结合对考题的难度分析，我校高三数学一轮复习调整策略，在必修五不等式的专题复习中加入选考4-5不等式选讲中的绝对值不等式的复习，并根据对考题的研究，从几种热门考点由易到难展开复习。

二、夯实基础，积累绝对值不等式解题方法

绝对值不等式的基础要求是掌握绝对值不等式的求解，难度较低，但仍有部分学生易出现计算错误。美国数学家哈尔莫斯：“数学的真正组成部分应该是问题和解，解题才是数学的心脏。”高三的复习课更是离不开解题能力的训练，解题能力训练的第一层次：利用通性通法，寻求题目的一种解法并得到正确的结果。从学生掌握知识的结构和认识问题的规律来说，首先是掌握解决这一类问题的方法，而不仅仅是解决其中某个问题的特殊方法。只有掌握了最通用的方法，才能达到通一法而通一类的效果。解绝对值不等式的题目关键是如何去掉绝对值符号，转化绝对值不等式为不等式，通法为零点分段法。

例1.解不等式： |x-2+|+|x-4|≤3.

解法一：（通法--零点分段法）将x的解分x≥4,2≤x＜4,x＜2三种情况讨论，得不等式的解集为

【注释】此解法易出现由于符号化简错误，要强调检验的方法，解集的两个端点值和即为方程的解，可代入检验。

解题能力训练的第二层次：一题多解，即在通性通法的基础上，寻求其他更简捷更巧妙的解法。将不等式的两侧分别看作两个函数，求两个图像的交点，结合图像得到不等式的解集，这种方法称为函数图像法。

解法二：（函数图像法）分三段作出函数的图象(如图1所示)

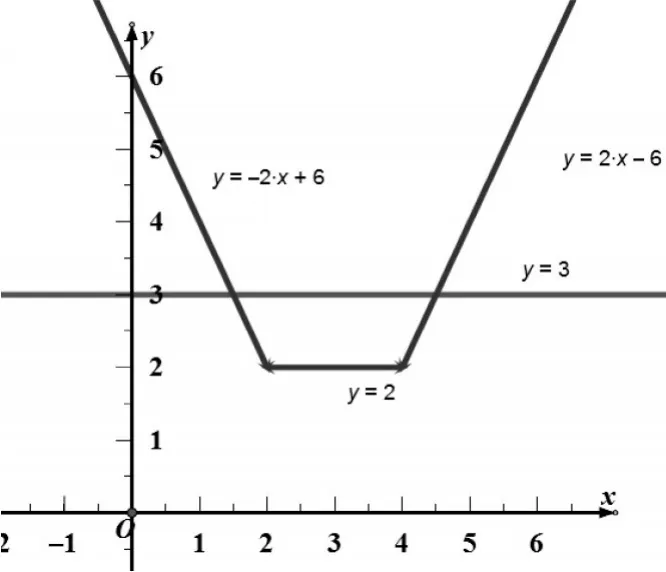
图1

【注释】解法三运用初中的绝对值定义，解法更直观简洁，可训练学生的直观想象能力，但多数学生在理解和运用上反而有一定难度，在文字描述上更是不知如何下笔，因此在平时的解题中多选用零点分段法或函数图像法。

三、建模训练，提升绝对值不等式解题能力

解题能力训练的第三层次：进行一题多变的训练，改变条件的叙述方式，改变条件的题设背景,改变设问方式,或把相似的几个题目组合改造,引申演变成新的问题。此环节要求教师跳进题海，准确把握绝对值不等式题型的变换特点，并具备对一些原题进行改编的能力。高质量、轻负担是教师努力的目标，提高学习效率最终要落实在课堂45分钟，复习课不能演变成讲评课，应精选例题，充分挖掘题目的内涵与外延，给足学生的思考时间，务必引导学生逐步掌握如何将未知的问题转化成可用已有的知识来解答，从而达到数学建模训练的目的。

（一）已知绝对值不等式的解集求参数的值

【注释】该例即为例题一的解法的逆用，解法主要参考一元二次不等式的解集与一元二次方程的解之间的关系，将不等关系转化为等量关系，学生的易错点是只代入一个解，而忽视这两个解必须同时满足。

（二）可利用化归转化分离参数的含参问题

不等式成立（恒成立）问题中的常用结论：

①若f(x)≥a恒成立，则f(x)min≥a；若f(x)≥a有解，则f(x)max≥a.

②若f(x)≤b恒成立，则f(x)max≤b；若f(x)≤b有解，则f(x)min≤b.

③若f(x)≥g(x)恒成立，则构造F(x)=f(x)-g(x)，F(x)min＞ 0.

将不等式的恒成立、有解等问题进行归纳，培养学生建模素养，理解各问题之间的关系，通过化归转化化难为易，积累解决此类问题的经验与方法。

∴4≥m+7即m≤-3

解法二（函数法）：

函数h(x)在(-∞,-1)上单调递减，在(3,+∞)上单调递增.

∴h(x)min=4

∴4≥m+7即m≤-3

【注释】解决恒成立问题的最常用方法是参数分离法，参数分离后将不等式问题转化为函数的最值问题。本例求最值采用绝对值三角不等式和分段函数单调性两种方法求最值，前者只针对两个绝对值内的式子的和或差为常数才可运用，有局限性，后者可视为通法。

【注释】将问题“存在x∈R使 | 2x+1|≤|x|+a成立”等价于“关于x的不等式 | 2x+1|≤| x|+a有解”，可转化为“(|2x+1|-|x|)min≤a”解答。

【注释】将问题“方程f(x)=a的解集为空集”转化为“a∉f(x)的值域”解答。

（三）不可参数分离的含参问题

参数与变量不易或无法分离时，可以利用数形结合、分类讨论、函数与方程等思想方法辅助解题，引导学生对试题进行归类总结。

解：因为 | 2x+2|-4≥4kx-5 解集为 R，所以|2x+2|≥kx-1在R上恒成立.

等价于函数y= | 2x+2|的图像不在函数y=kx-1的下方，可得k∈[-1,2]

【注释】不等式 | 2x+2|≥kx-1参数分离需要考虑x的符号不易操作，反而是利用不等式两侧的两个函数图像间的关系，将不等式问题转化成直线间的斜率大小问题，难度大大降低。

例5.已知函数f(x)=-x2+ax+4,g(x)=若不等式 f(x)≥g(x)的解集包含[-1,1]，求a的取值范围．

解：因为不等式f(x)≥g(x)的解集包含[-1,1]

∴ 在［-1,1］上不等式 d(x)≥g(x)恒成立，即-x2+ax+4≥|x+1|+|x-1|恒成立

∴在［-1,1］上-x2+ax+4≥(x+1)-(x-1)，即-x2+ax+2≥0

Q函数h(x)=-x2+ax+2开口向下

∴在［-1,1］上h(x)min=h(-1)或h(1)

【注释】将问题“不等式f(x)≥g(x)的解集包含［-1,1］”转化为“在［-1,1］上不等式f(x)≥g(x)恒成立”解答。不等式-x2+ax+2≥0在［-1,1］上分离参数反而需要分类讨论，直接运用二次函数的图像单调性确定最值只在端点处产生。

对学生通性通法、一题多解、一题多变这三个层次的训练，注重分类讨论、参数分离、数形结合、化归转化等数学方法的渗透，不仅学活了知识，更重要的是完善了绝对值不等式的解题模式，达到锻炼思维品质，培养创新思维能力的目的。