基于引文网络入度分布的投稿推荐研究
2019-08-15谭智敏刘万国2沈洪杰郭淑艳
谭智敏,刘万国2,沈洪杰,郭淑艳
助力重点学科教学及科研活动是高校图书馆开展学科服务工作的重点。投稿推荐是学科服务中关键的服务项目,影响到科研成果被接受的速度和科研影响力。目前投稿推荐算法相关研究比较少,主要是对引文网络数据进行分析[1-3]。引文网络中论文也被称为“引文网络的入度”。引文网络入度在不同期刊上的分布包含引文网络入度的基本特征,对引文网络入度的研究有利于从根本上简化投稿推荐算法的计算量、增加投稿推荐的精度。
目前已有的引文网络入度分布研究表明[4-6],文献分布已经从满足幂律分布[7-9]逐渐出现偏离幂律分布的现象[10]。对于偏离幂律分布的研究主要是对幂律分布形式上的修正。对于偏离幂律分布的现象给予一个微观模型解释,有利于深入了解引文网络入度分布的变化机制以及设计更精确的投稿推荐算法。
1 研究方法及模型的建立
本文基于国内9所农业类大学发表论文的统计数据,研究建立一个引文网络入度分布模型,是为了方便研究引文网络中偏离幂律分布的机制,有利于建立或修改文献推荐模型,提供更好的文献推荐或者投稿推荐。
1.1 数据采集及研究方法
本文以Web of Science核心合集作为数据检索平台,对中国农业大学等9所农业类大学发表的论文进行检索,共得到94 836条记录并下载。将各高校发文按期刊分类分别保存,以备后续数据统计分析和拟合。数据采集时间为2018年7月9日。
1.2 发表期刊分布统计模型的建立
图1显示了期刊发表概率的统计分布,其中(a)部分是正常坐标的统计分布,(b)部分是双对数坐标的统计分布。图1中的蓝圈是数据统计结果,红线是拟合结果。
对Web of Science核心合集下载的论文数据按发文期刊做统计分布,并按照期刊发文的数量做降序排列并做归一化处理,得到发表期刊的概率分布,可以得到如图1(a)中蓝色圆圈描述的数据,数据结果显示概率密度随着期刊序号的增加快速衰减,呈幂律分布。对于这类结果,早有学者开始研究,而近期的研究结果又出现一些偏离幂律分布的情况。如果数据分布满足幂律分布,那么对概率分布和期刊序号分别做对数,结果应该是一条直线。对图1(a)中的数据取对数,结果如图1(b)中蓝色圆圈,红线是根据幂律分布拟合的结果,数据结果表明排名靠后的部分是偏离直线的。在正常坐标下统计数据和拟合结果差别较小,但在取完对数后可以明显看出其偏离幂律分布。已有研究者开始关注偏离幂律分布的现象,然而到目前为止还没找到一个合适的模型能精确拟合和解释偏离幂律分布的现象。为了更好地解释数据,本文通过抽象论文发表状态和状态转移速率,建立了一个类似动力学过程的模型,并得到了扩展指数模型和指数模型求和的拟合方程,可以有很好的拟合效果。
图1期刊发表概率的统计分布
本文根据论文发表的状态和状态之间的转移概率来推导论文发表的概率分布公式。因为论文投稿、最终发表到哪一种期刊是受很多随机因素影响的,如实验数据的质量、文章的切入点、写作质量、选择的投稿期刊、审稿人对研究方向是否感兴趣等。因此这里先假定论文写完后,最终一定会发表,也就是说本文的研究对象是所有指定高校发表的论文总体。由于每所高校发文的期刊会有一个统计分布,把这个统计分布结果按期刊发文数量做降序排列就得到了一个固定的期刊序列,所以假定任何一个高校都有一个期刊序列,一般情况不同高校对应的序列是不同的,并且也有可能是随时间变化的。在论文完成后,按照上面假定的期刊序列尝试投稿,如果论文在当前期刊会有一定的概率发表,如果没有发表,那就按概率随机转移到下一期刊,直到论文被发表,这样就使期刊序列和时间演化相对应。论文在当前期刊上发表的概率用PA表示,未发表用PB表示,这样就存在A和B两个状态,分别代表在当前期刊上“发表”和“未发表”,从状态A到状态B存在一个概率转移速率k1。
因为不能确定高校最终发表期刊的序列,为了不失一般性,还需要定义一个逆向的迁移速率k-1,这样论文发表的期刊统计分布就可以类似于动力学过程,建立模型如下:
式中,A代表发表的状态,B代表未发表的状态。通过以上模型可以写出A和B的概率分布演化满足的方程(1):
(1)
方程的初始条件如方程(2)所示:
(2)
即初始的时候论文处于未发表的状态。然后根据方程(1)和(2),求解论文发表状态的概率演化过程,其结果就等价于发表期刊的统计分布。根据方程(1)和(2)所描述的微分方程和初始条件可以得到解析解,B状态的概率演化为:
结果是指数形式。模型里面概率转移速率是一个常数。而在真实情况下,高校中的每个个体可以近似看成一个常数。对于整个高校来说,k1和k-1有很多个可能的取值,这些取值满足的概率分布用p(k1)来描述。为了简化模型,假定k-1是不变的,所有需要变化的统计分布都等价地放在p(k1)中描述。这样B状态的概率演化就需要对所有可能的k1值进行积分:
这个积分形式看起来比较复杂,并且一般不知道p(k1)的具体形式,所以没有办法直接计算或者拟合数据,因此需要对其继续简化。当k1远远小于k-1时,被积分项中(k1+k-1)都可以直接简化成k-1,k1的积分上限也可以用k-1代替,因此可以简化成如下形式:
上述积分形式可以进一步简化成为e指数形式:
PB(n)=A1e-k-1n
式中A1是为了拟合数据需要变化的振幅,如果拟合的是概率,那么A1就对应着归一化常数。
当k1远远大于k-1时,B的概率演化就变成了一系列e指数的加权求和的形式,也可以用积分的形式表示:
对于这个积分项,已经有过相关研究,可以简化成下面这样一个扩展指数形式[11]:
PB(n)=A2e-(k1n)β
因此拟合方程可以近似写成上面两个公式的和:
PB(n)=A1e-k-1n+A2e-(k1n)β
(3)
式中A1、A2、β是拟合参数,其中β是处于0到1之间的数。可以用上述扩展指数模型对各科研机构发表期刊的统计结果进行拟合。
2 数据统计及拟合
本文采用上述国内9所高校的94 836条记录验证模型,将这些记录按学校分类,再按发表期刊进行统计。
2.1 发表期刊概率分布及扩展指数模型拟合
对每所高校的发文期刊做出统计分布,并用公式(3)拟合。其中,中国农业大学的数据拟合结果如图2所示,可以看出数据在正常坐标下拟合很好。为了查看更精细的拟合效果,我们在图2(b)给出了双对数坐标的拟合结果,在双对数坐标下拟合效果也很好。为了验证方程的普适性,用这个方程分别对9所高校的发文数据进行拟合,拟合结果如图3所示。图3中蓝色点是统计结果,红线是拟合曲线;学校的排序不分先后,按英文名称的字母排序。为了方便直观地查看拟合结果质量,我们直接采用双对数坐标给出拟合结果。从图3中可以看出,各个学校的数据拟合效果都很好,没有出现拟合结果和统计数据偏离的情况。
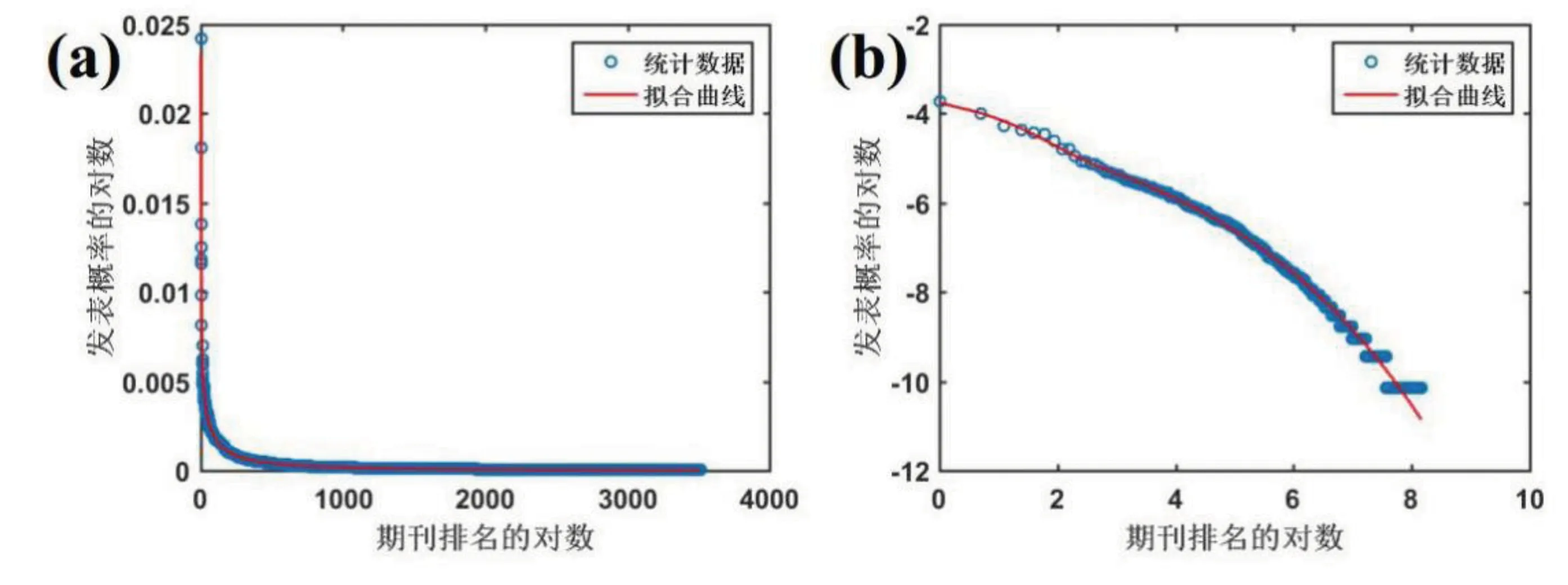
图2中国农业大学发文期刊数据扩展指数模型的拟合效果
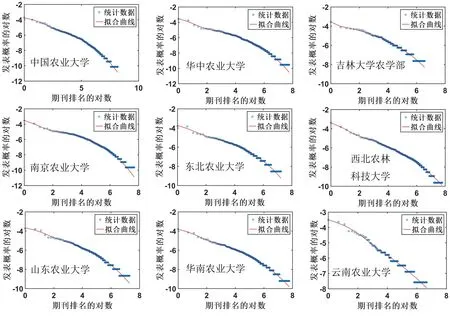
图3 9所高校发表期刊的统计结果及其拟合曲线
2.2 扩展指数模型的拟合误差
为了更精确量化描述模型的拟合效果,我们采用了几个常用的误差值来分析,并与幂律分布对比。采用的几个误差项分别是误差的平方和(SSE)、Pearson相关系数(R)和均方根误差(RMSE)。
误差平方和(SSE)又称“残差平方和”,根据观察值拟合适当的模型后,余下未能拟合部分称为“残差”,对所有“残差”平方之后求和就得到了拟合的SSE值,其大小可能表明函数拟合得好坏。其计算公式如下:
式中,yi是统计出来的数据,zi是用模型拟合后的数据,N是数据的个数。从公式中可以很容易看出,SSE数值越小拟合越好。
Pearson相关系数用来衡量两个数据集合是否在一条线上面,即衡量定距变量间的线性关系。其计算公式如下:
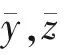
均方根误差是观测值与拟合值偏差的平方与观测次数N的比值的平方根。计算公式如下:
均方根误差在测量过程中对特大或特小误差反映较敏感,所以实际拟合的过程中经常用来描述拟合结果的好坏。从公式中可以看出,参数值越小越好。
为了反映拟合效果,我们把扩展指数模型和当前广泛使用的幂律模型拟合对比。
表1给出了用两个模型拟合的结果以及各个学校对应的拟合参数,分别用SSE、R、RMSE描述拟合效果。从表1中的数据可以看出扩展指数模型明显优于幂律分布,其中SSE和RMSE反映的是精度,说明本文中的模型比幂律分布高一个数量级。
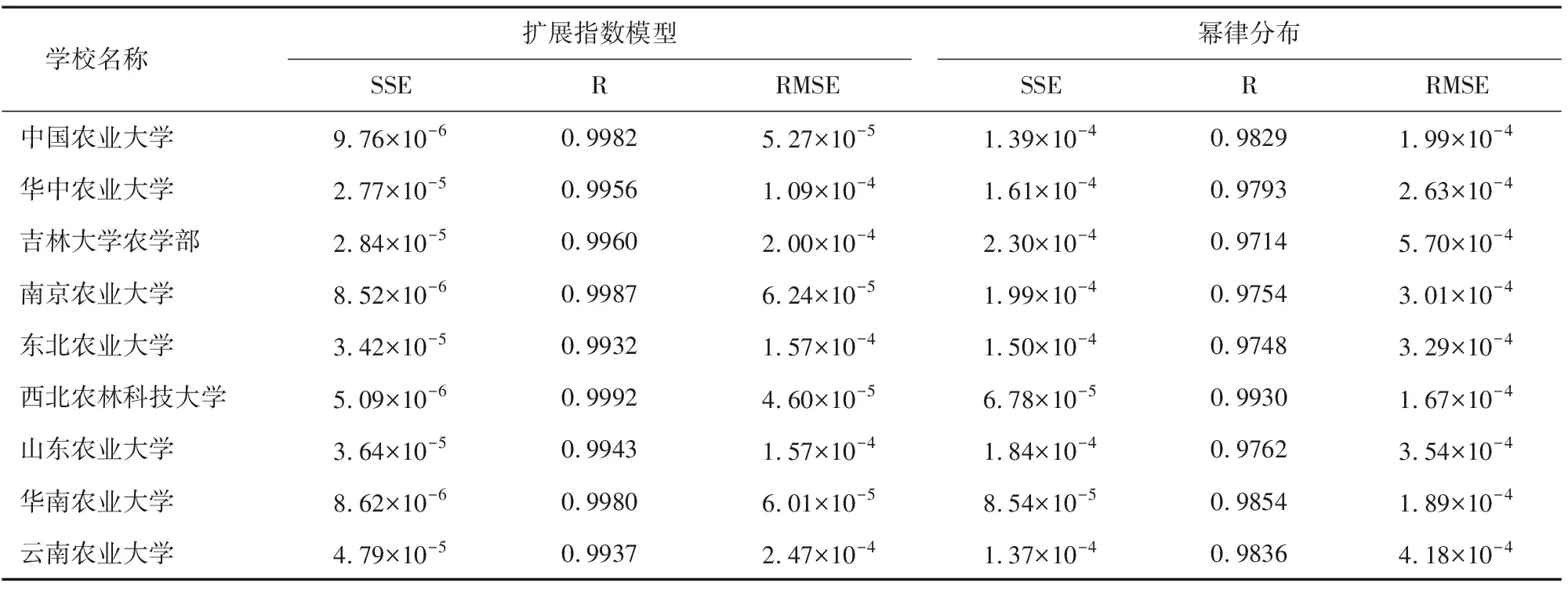
表1 扩展指数模型和幂律分布模型的拟合效果对比
3 模型解释及参数的意义
扩展指数模型对各高校发文的统计分布拟合效果(表2)较好,但为了使模型能更广泛地使用,需要对模型的意义及参数进行详细了解。从表2可看出,各个参数大概都在一个比较小的范围内浮动,这有可能都是涉农学科的原因。本文建立模型时使用了一个比较抽象的模型,其中的状态转换速率(k1,k-1)、归一化常数(A1,A2)以及扩展指数(β)都很难对应现实中期刊发表过程的常用量。因此本文通过公式模拟给出各个参数变化时论文发表概率分布的变化。
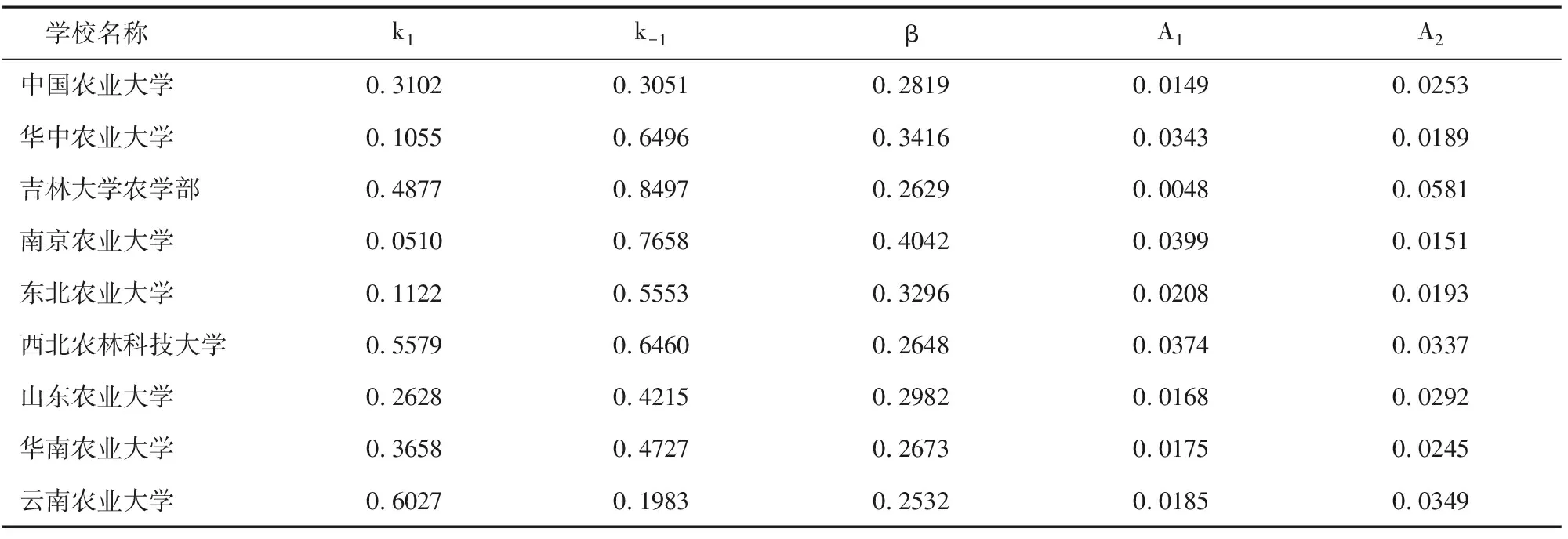
表2 各高校数据通过扩展指数模型的拟合参数列表
图4中给出了振幅量的变化对整个概率分布的影响。为了更清晰地表达图4结果的变化,我们选取了双对数坐标。
图4(a)显示了指数公式的振幅变化对概率分布的影响。参数值选取的范围是表2中A1拟合结果的上下限,其他参数用各高校的参数的平均值。从图4(a)可以看出,排名靠前的期刊受A1的影响,并且随着A1的增加,曲线是向上偏移的,而排名靠后的期刊几乎没有受到影响。从图4(b)可以看出当振幅A2增加时曲线的变化,随着A2的增加曲线也是向上移动的,排名比较靠后的期刊移动得比较大。
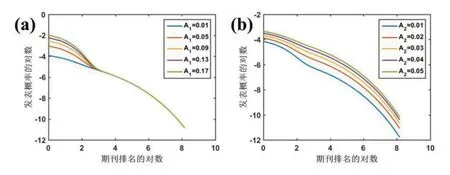
图4 扩展指数模型中两个振幅量对概率分布的影响
图5中给出了模型中转化速率对概率分布的影响。从图5(a)可以看出,随着指数分布的逆向速率k-1增加,排名靠前的期刊受到的影响比较大,并且随着速率常数的增加概率分布逐渐减少。从图5(b)可以看出,随着扩展指数模型中的速率k1增加,排名靠后的期刊概率分布减少得比较多。
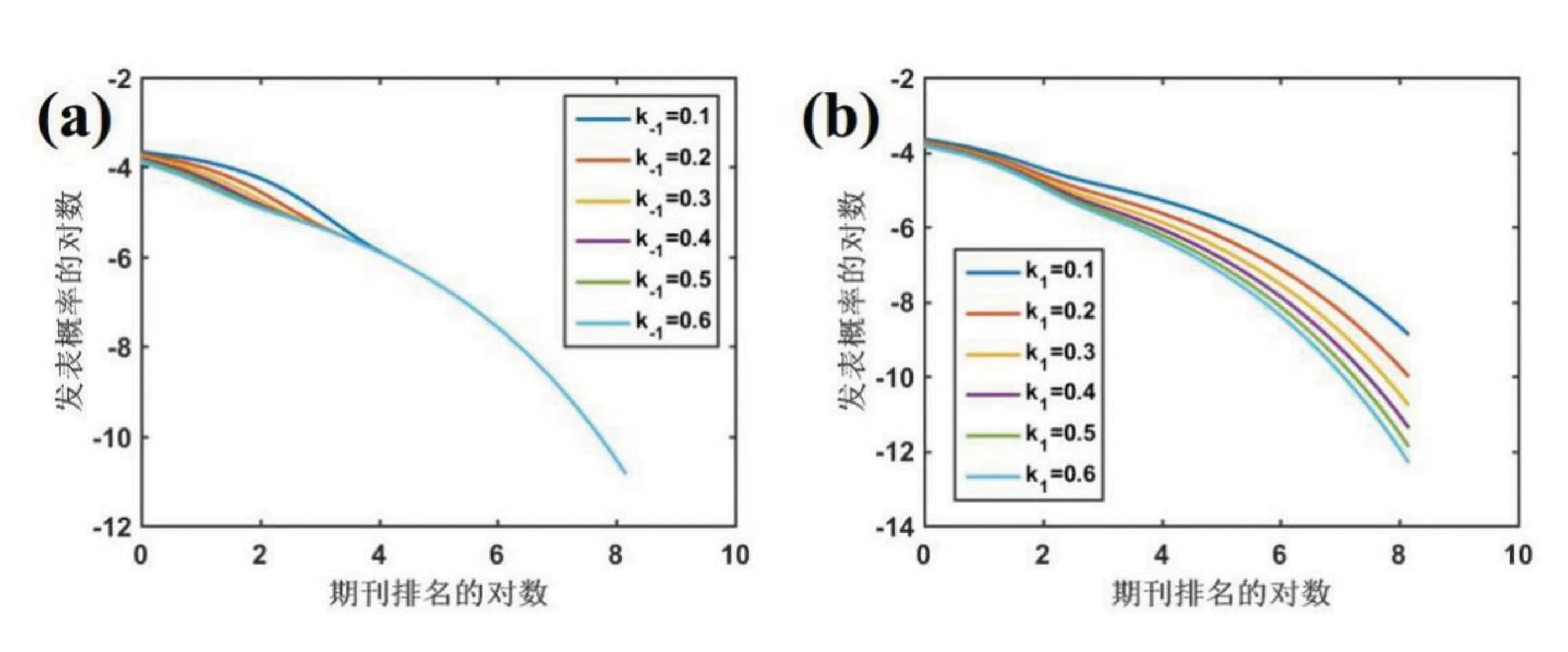
图5 扩展指数模型中两个速率变化对概率分布的影响
图6给出了扩展指数β的变化趋势。排名靠后的期刊的概率分布随着β的增加减少,排名靠前的期刊基本上未受影响。
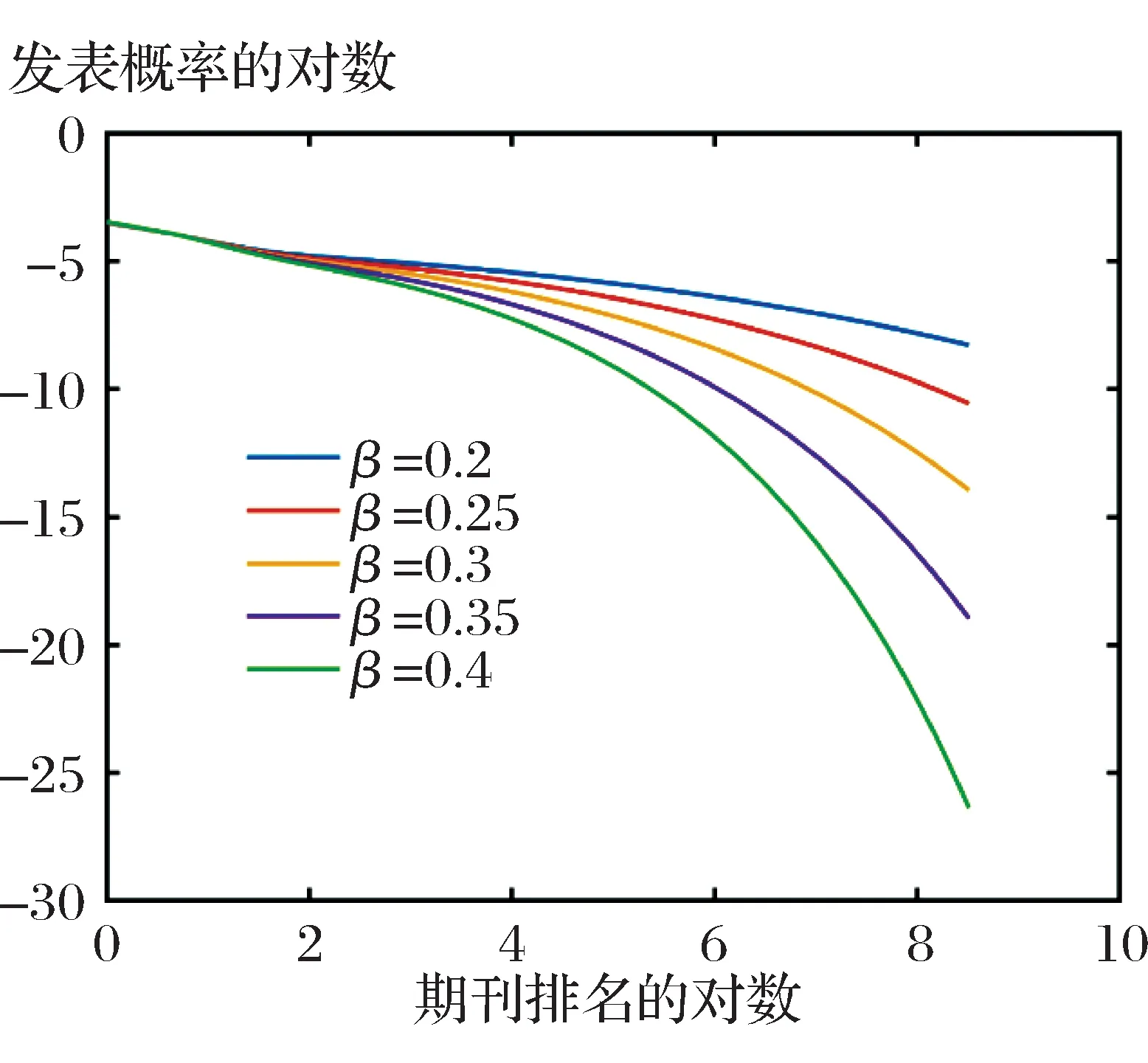
图6 扩展指数模型中扩展指数对概率分布的影响
当β趋近于0时,排名靠后的期刊的概率分布接近单指数分布,即越接近幂律分布。
通过了解各个参数对整体分布的影响,就可以把该模型应用到某个具体科研机构。对科研机构在不同时间段内发表论文的概率分布进行拟合,可以得到参数随时间的变化趋势,参数的变化趋势可反映科研机构中科研政策的变化。
4 模型的潜在应用
本文建立的模型可以应用于图书馆学科服务之投稿推荐。本模型中包括k1,k-1这两个拟合得到的概率转移速率,这两个速率在实际应用中对应着在投稿序列中正向和逆向迁移速率。笔者通过设置不同的初始投稿期刊及拟合出来的速率,利用计算机模拟给出不同初始投稿期刊下投稿次数的统计分布。模拟过程如下:给定一个初始投稿期刊,通过最终发表概率,用随机数判断当前期刊是否发表。如果发表就记录投稿的次数,如果没有被发表,就按概率转移速率转移到下一期刊,并且投稿次数加1,直到论文被接收,记录投稿次数。为了得到稳定的概率统计分布,笔者进行了100 000次投稿模拟,得到的概率分布如图7所示。由于采用的概率是一个机构的整体概率,因此投稿次数会比正常的投稿次数高,需要找到一个参考值。这里的参考值选取是通过完全随机的选取期刊投稿,并计算是否被接收,记录过程与前面模拟过程一样,只是选取期刊的方式不同,是一个完全随机的过程。模拟结果如图7所示,图中的数字代表初始位置,比如10%就是指初始位置在整个期刊序列中前10%,随机就是完全随机的模拟。随着选取的初始位置增加,投稿次数会明显增加,但都比随机模型低很多,说明本模型可以很方便地应用到投稿推荐,并可明显提高投稿接收速度。但由于本文讨论的数据是整个机构的统计数据,得到的投稿次数很大。如果要应用到个人的投稿推荐,需要对个人发表期刊进行统计分布,或者建模分析。由于本模型可以得到较好的次数,因此有潜力应用到个人投稿推荐。通过概率转移速率也有可能模拟这个机构未来发表论文的分布。
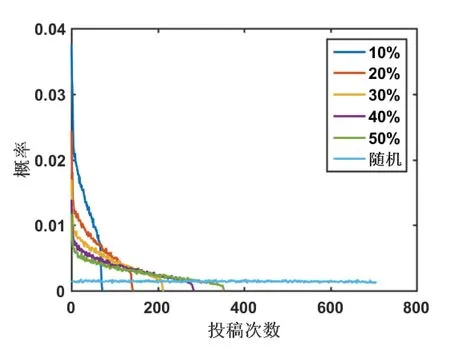
图7 概率随机模型用于投稿推荐与完全随机模型对比
5 结论
研究科研机构发文对应的期刊分布,对于理解引文网络结构特征、科学定义文献计量指标以及对于学者更好地了解学科发展状况、促进科研发展等都起着非常重要的作用。以前只是采用布拉德福定律和幂律分布解释文献分布规律,但随着论文发表和下载获取方式的变化,其分布也偏离了原来的分布。本文通过建立动力学过程求解出一个概率分布,即e指数和扩展指数求和的形式,并用它拟合了国内9所涉农学科高校发文期刊的分布,通过与以往拟合模型对比,效果优于广泛使用的幂律分布模型。通过模拟给出各个参数的意义以及各个参数变化时分布的变化,方便对科研机构实时数据做分段拟合,给出参数随时间的变化,分析科研机构中科研政策的影响等。该模型可以应用到投稿推荐上。
本文建立的扩展指数模型相比于幂律分布,解析式相对较复杂,但可以得到更接近实际发表论文的期刊分布。从实际情况来看这种改进是合理的,可为今后有效合理地利用期刊计量指标提供科学依据。
