例析圆锥曲线三类弦问题求解策略

蔡海涛

(福建省莆田第二中学 351131)

解析几何是高考数学的重要考查内容，常作为试卷中高分选拔的试题.而直线与圆锥曲线位置关系问题又是解析几何中常见的重要类型,纵观近年来的高考题,圆锥曲线三类弦问题问题须引起我们关注.本文例谈这几类问题,并探究其求解策略.

在解决直线与圆锥曲线的弦长问题时，通常应用韦达定理与弦长公式.若涉及到“三类弦”(焦点弦、中点弦、原点弦)问题，则可根据各自的几何特征，简化运算，巧妙求解.

一、焦点弦

例1 (2018年高考全国Ⅱ卷·理19)设抛物线C：y2=4x的焦点为F，过F且斜率为k(k>0)的直线l与C交于A，B两点，|AB|=8．

(1)求l的方程；(2)求过点A，B且与C的准线相切的圆的方程．

解(1)由题意得F(1,0)，l的方程为y=k(x-1)(k>0).

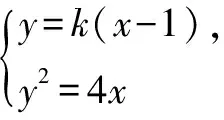
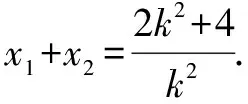
(2)所求圆的方程为(x-3)2+(y-2)2=16或(x-11)2+(y+6)2=144.(过程略)

评注本题直线l过焦点F，故|AB|的长即为焦点弦长，所以把|AB|转化为|AF|与|BF|两条焦半径的和，再利用定义，把这两条焦半径转化为到准线的距离，问题得以解决.一般地，焦点弦问题常常可以利用定义来解决，可使得运算简化，轻松求解.

二、中点弦

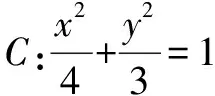
解(1)设A(x1,y1),B(x2,y2)，

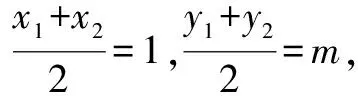
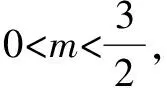
评注与圆锥曲线的弦的中点有关问题,我们称之为圆锥曲线的中点弦问题.一般地，中点弦问题通常可以利用“点差法”，使得运算简化，快速解决问题.

三、原点弦

(1)求椭圆的方程；

(2)设直线l:y=kx(k>0)与椭圆在第一象限的交点为P，且l与直线AB交于点Q.

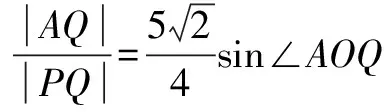
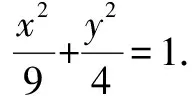
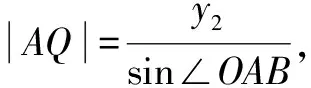
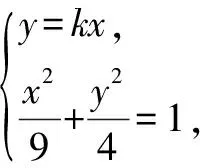
两边平方，整理得56k2-50k+11=0

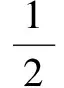
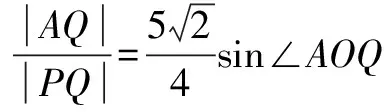
四、巩固训练

(1)试证：若a、b、c不是等比数列，则椭圆E一定不是黄金椭圆；

(1)证明：点P在C上；

(2)设点P关于点O的对称点为Q，证明：A、P、B、Q四点在同一圆上．

3.(1)略；(2)A、P、B、Q四点在以N为圆心,NA为半径的圆上.