例谈利用导数判断带参数函数的单调性

龚亮亮

(江苏省南京市第三高级中学 210000)

导数是研究函数的重要工具，利用导数来判断函数的单调性是近几年高考重点考查内容.本文通过例题分析，对解决带参数函数的单调性这一类问题进行总结.

例1求函数y=3x2-2lnx的单调减区间.

例2已知f(x)=ex-ax-1,试求f(x)的单调递增区间.

分析要求f(x)的单调递增区间，由于定义域为R，只需对函数求导，令导数大于零即可.但导数f′(x)中带有参数，怎么办？因此，需要我们对参数a进行讨论.那么讨论的标准呢？笔者认为要抓住导函数是否存在零点，因此需要对a的正负进行讨论.

解∵f(x)=ex-ax-1,∴f′(x)=ex-a.

令f′(x)≥0，得ex≥a.

当a≤0时，有f′(x)>0在R上恒成立；

当a>0时，有x≥lna.

综上，当a≤0时，f(x)的单调增区间为(-∞,+∞);

当a>0时，f(x)的单调增区间为[lna,+∞).

反思：本题求导以后是关于x的二次函数，参数在常数项位置，因此直接仿照例2对参数a进行讨论即可.

例3设函数f(x)=a2lnx-x2+ax，a>0，求f(x)的单调区间.(注：e为自然对数的底数)

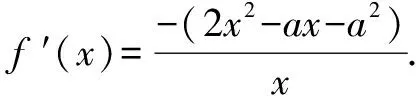
读者可以思考：若a∈R呢？

分析对函数f(x)求导以后跟例3一样，也只需对分子部分的二次式x2-ax+2讨论即可.但跟例3比较也有不同之处，本题二次式x2-ax+2不可直接因式分解，怎么办？如何讨论？

当Δ=a2-8<0，对∀x>0,f′(x)>0.∴f(x)在(0,+∞)上递增.

当Δ=0，∴f(x)在(0,+∞)上递增.

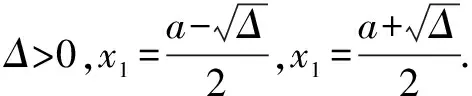
故在(0,x1)增，在(x1,x2)减，在(x2,+∞)增.

反思本题求导以后需讨论的分子部分也是关于x的二次函数，参数在一次项位置，但不能直接因式分解，因此仍然抓住函数的零点，通过判别式结合图象对参数a进行讨论.

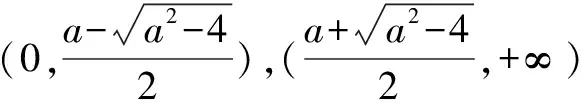
例5已知函数f(x)=(a+1)lnx+ax2+1,讨论函数f(x)的单调性.

分析本题因为定义域为(0,+∞)，因此仅需对求导后的分子部分进行讨论.由于x2前面带有参数a，因此判断2ax2+a+1是否存在零点，首先要对a是否为0进行讨论.还要注意到常数项是a+1，因此还需对a进一步讨论.

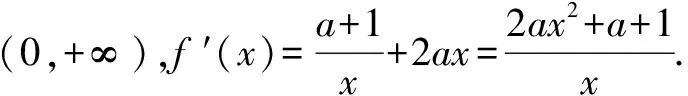
当a≥0时，f′(x)>0,故f(x)在(0，+∞)单调递增；

当a≤-1时，f′(x)<0,故f(x)在(0，+∞)单调递减；

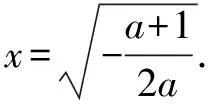
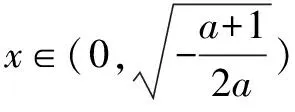
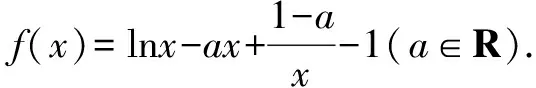
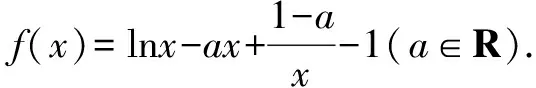
令g(x)=ax2-x+1-a,x∈(0,+∞),

(1)当a=0时，g(x)=-x+1,x∈(0,+∞),所以当x∈(0,1)时，g(x)>0，此时f(x)<0，函数f(x)单调递减.

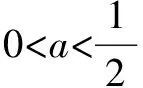
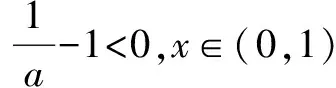
x∈(1,+∞)时，g(x)<0,此时函数f′(x)<0单调递增.

综上所述：当a≤0 时，函数f(x)在(0,1)上单调递减,在 (1, +∞)上单调递增；

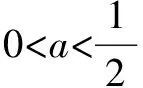
反思本题关键是对g(x)=ax2-x+1-a进行分析讨论，与例5相比g(x)多了一次项.但问题解决的关键仍然是对g(x)=ax2-x+1-a的零点进行讨论.

由此可见，利用导数求带参函数的单调区间，往往到最后即转化为对导函数中的二次函数部分进行的讨论问题，题目难度可随参数位置不同而不同.当然，我们分类讨论的时候只要抓住了导函数是否存在零点，如果存在零点, 零点是否在定义域内以及零点是否相等,一般都可以将问题解决.