东南沿海地区玄武岩残积土雨水运移特征及滑坡失稳数值模拟
2019-08-14张晨阳张泰丽伍剑波王赫生
张晨阳,张泰丽,张 明,孙 强,伍剑波,王赫生
(1.中国地质大学(武汉)工程学院,湖北 武汉 430074;2.中国地质调查局南京地质调查中心,江苏 南京 210016)
玄武岩残积土在我国广泛分布,其性质较为特殊,具有亲水性强、高孔隙比、易湿化崩解等特征[1]。大量研究结果表明,玄武岩残积土本身的微裂隙较多,渗透性强,在降雨入渗过程中,通过裂隙的优势流加速了雨水的入渗,土体含水量逐渐增大,基质吸力随之降低,抗剪强度减小,最终影响残积土斜坡的稳定[2-3],导致斜坡失稳[4-5]。我国东南沿海地区玄武岩残积土斜坡分布较广,暴雨期间极易失稳[6-9],而该地区玄武岩残积土的入渗特性及滑坡失稳机制研究程度较低,因此有必要对其进行研究。
残积土中的降雨入渗过程十分复杂,且在斜坡原位进行观测较为困难[8],因此室内土柱试验是研究残积土降雨入渗特征的重要手段。朱伟等[9]利用土柱实验探讨了降雨强度和时间对土壤水分重分布的影响。Gofar等[10]进行了室内土柱实验,探讨了降雨对土壤孔隙水压力分布的影响。Rao等[11]通过土柱实验对森林覆盖土进行了一系列渗透性质的研究,在此基础上改进了Green-Ampt入渗方程。以上研究采用的均是重塑土,由于天然状态下玄武岩残积土内存在大量的残余结构,采用重塑土必然与真实情况有较大差异[12];且上述研究中通过土柱实验获取的降雨入渗特征未应用到滑坡的稳定性分析中。本文以浙江省温州市马济头玄武岩残积土滑坡为对象,利用原状土土柱实验,获取中峰型与前峰型两种降雨工况下玄武岩残积土的雨水运移特征,获取最符合玄武岩残积土入渗特征的土水特征曲线及渗透函数;然后将上述曲线应用于滑坡的渗流场和稳定性变化研究中。
1 马济头滑坡概况
马济头滑坡位于浙江省温州市大峃镇马济头村,滑坡整体呈圈椅状,纵向长约60 m,宽约38 m(图1)。滑坡所处区域地貌为低山丘陵,局部地形上陡下缓,前缘高程476 m,后缘高程512 m,相对高差36 m,总体坡向82°。坡体表层覆盖玄武岩残积土,层厚3~6 m,红褐色,原岩结构已不可见,成砂、黏土状。基岩地层为中生代白垩系朝川组玄武岩,黑褐色,无斑隐晶质结构,气孔构造。
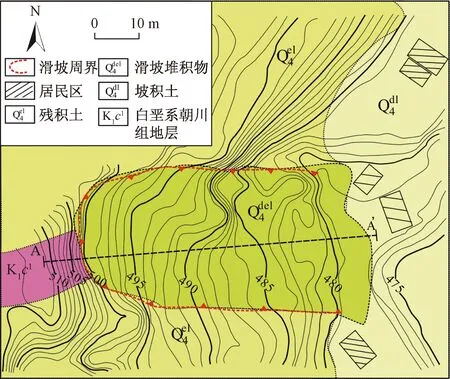
图1 马济头滑坡平面图Fig.1 Map of the Majiton landslide
原始斜坡在2016年鲶鱼台风暴雨期间发生整体滑动,对坡脚32户居民产生了较大的威胁。由现场勘察资料可知,滑坡上覆的玄武岩残积土沿着基覆面整体失稳,滑面呈圆弧形,在残积土层内。滑坡失稳后,整体呈圈椅状。滑体堆积在坡脚位置,体积约10 000 m3(图2)。
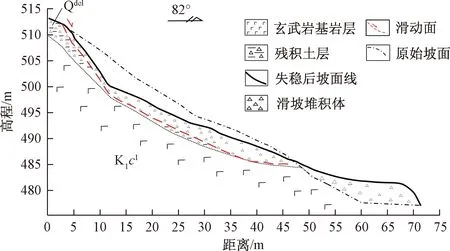
图2 马济头滑坡A-A′剖面图Fig.2 Geological profile alonp line A-A′ of the Majitou landslide
2 降雨入渗土柱实验
为了获取玄武岩残积土的雨水运移特征,在坡体取2个原状土土柱,分别在室内进行中峰型与前峰型2种降雨工况下的降雨实验。
2.1 实验设计
2.1.1实验装置
整个实验装置包括模拟降雨系统、土柱装置和数据采集系统。模拟降雨系统包括马氏瓶和针管式模拟降雨器。降雨强度通过马氏瓶的高度来控制。经过率定,实验使用的降雨强度10,30 mm/h所对应的马氏瓶高度分别为150,165 cm。土柱装置为一圆形有机玻璃筒,直径30 cm,高度150 cm(图3)。上部25 cm支撑降雨器,下部125 cm放置原状土土柱。离土体表层2 cm的位置设有出口A,当降雨强度较大时,土体表层可形成积水,模拟斜坡表面的片流。筒边壁预设6个方孔,距土体表层深度为10,20,30,45,65,95 cm,以放置体积含水率探针。土柱的底部设置多孔底板和排水孔B,用于排水。
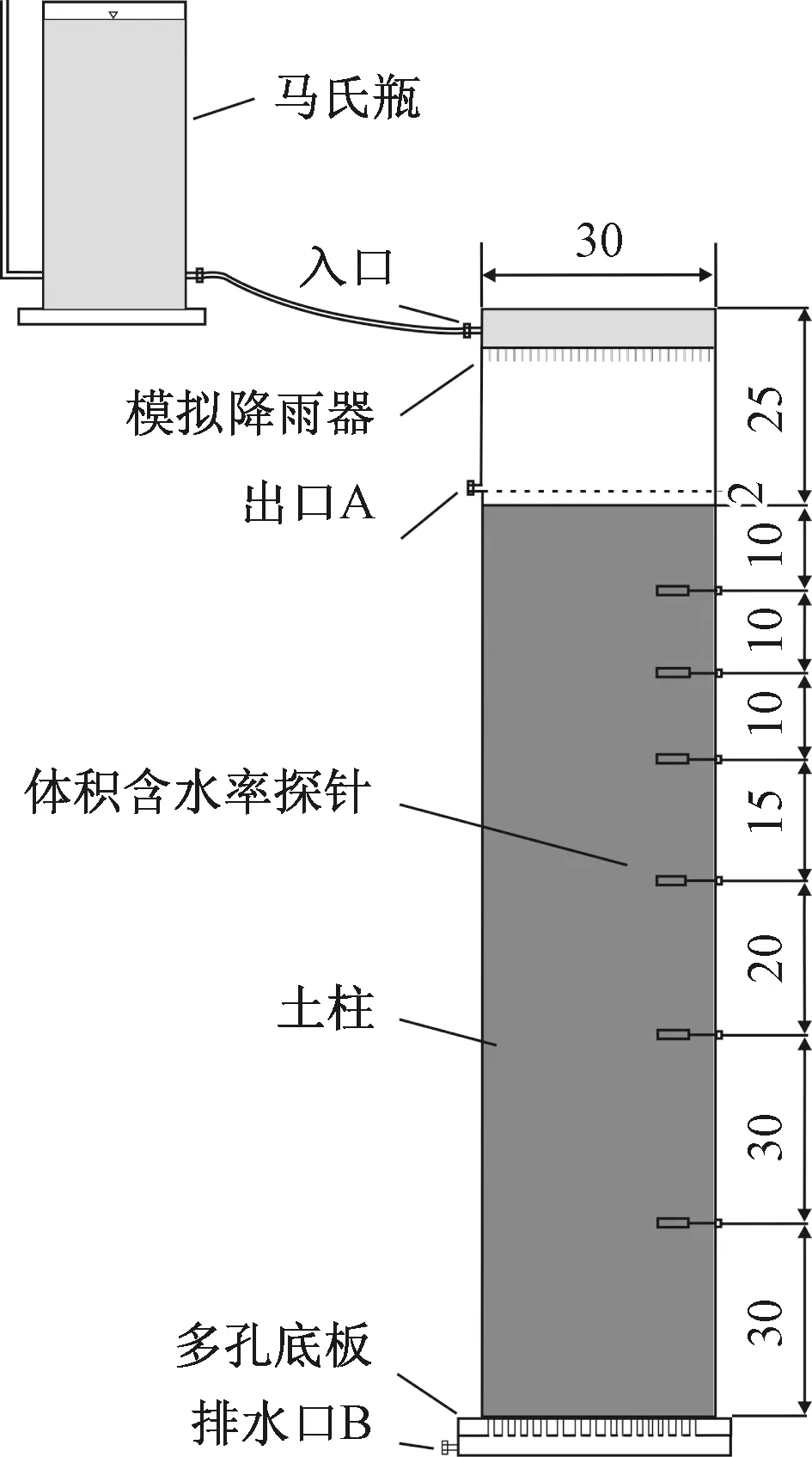
图3 实验装置示意图(单位:cm)Fig.3 Sketch of the experimental devices
数据采集系统包括FDR湿度计、数据采集仪和电脑。FDR湿度计的测量范围为0~100%,误差为±3%,使用前需通过实验土样校正。体积含水率探针插入6个方孔中实时监测土壤体积含水率,并通过数据采集仪传输到电脑中。
2.1.2实验降雨工况
统计研究区近年来的台风降雨记录,总结得到的台风暴雨期降雨特征如下:①一次降雨事件持续时间多为3 d左右;②降雨峰值多发生在第二天,但也有少量发生在第一天,该天平均降雨量约300 mm,其它两天降雨量较小,平均降雨量约50 mm;③降雨强度随着时间分布极不均匀,一天的降雨量往往集中在数小时内[13]。根据以上特征,我们设置中峰型(ABA)与前峰型(BAA)两种降雨工况。ABA型降雨工况下,第一天前5小时为降雨期,降雨强度为10 mm/h,其余19个小时为间歇期;第二天前10小时为降雨期,降雨强度为30 mm/h,其余14小时为间歇期;第三天与第一天相同,三天的总降雨量为400 mm。BAA型降雨工况下,第一天前10小时为降雨期,降雨强度为30 mm/h,其余14个小时为间歇期;第二天前5小时为降雨期,降雨强度为10 mm/h,其余19小时为间歇期;第三天与第二天相同。
2.1.3取样
为了保持残积土的原始状态,取样时,先将有机玻璃柱缓慢压入土层,并从四周逐渐开挖,边压边挖,直至设计深度。在滑坡同一位置取1号和2号两个土柱,取样完成后用塑料薄膜将其密封,运回实验室。1号土柱进行中峰型降雨,2号土柱进行前峰型降雨。
2.1.4数据采集及处理
实验过程中,定时采集土柱内10,20,30,45,65,95 cm深度处的体积含水率。降雨期采集间隔为1 min,间歇期为30 min。
2.2 结果分析
2.2.1土柱初始孔隙水压力分布
土体初始的水势分布反映了其前期的降雨情况,控制着土体的雨水运动特征[14]。实验开始前利用张力计获取2个土柱的初始孔隙水压力分布。2个土柱的初始孔隙水压力的分布整体较为相似,1号土样在20 cm深度的孔压最大,约-26 kPa,其余深度的初始孔压较为一致,约-28 kPa;2号土样在10 cm深度的孔压最小,约-32 kPa,30 cm深度的孔压最大,约-26 kPa,其余深度的孔压约-30~-29 kPa。
2.2.2体积含水率变化征
图4~5分别是ABA和BAA型降雨工况下,土柱内不同深度的体积含水率变化曲线。
ABA型降雨工况下,第二天降雨期间,土柱内各深度的体积含水率最大,第三天降雨期间大于第一天;降雨间歇期内土柱的体积含水率随降雨天数的增加逐渐增大,第一天间歇期最小,第三天间歇期最大。土柱内10,20,30,45,65,95 cm深度的初始体积含水率分别为32%、32%、30%、33%、32%、34%。第一天降雨3 h内,土柱内体积含水率从上到下依次增大,20,30,45,65 cm深度增大约5%~8%,10,95 cm深度增大约20%;降雨结束后4 h,20,30,45,65 cm深度体积含水率降低3%~5%,10,95 cm降低约15%。第二天降雨1 h内,土柱内体积含水率从上到下依次迅速增大,30,45,65 cm深度增大5%~8%,10,20,95 cm深度增大约22%;降雨结束后各深度体积含水率迅速下降,30,45,65 cm深度降低约5%,10,20 cm深度降低约10%,95 cm深度降低约20%。第三天降雨3 h内,土柱内体积含水率从上到下依次增大,30,45,65 cm深度增大5%~8%,10,20 cm深度增大7%,95 cm深度增大15%;降雨结束后,30,45,65,95cm深度体积含水率降低约5%,10,20 cm深度降低约10%。
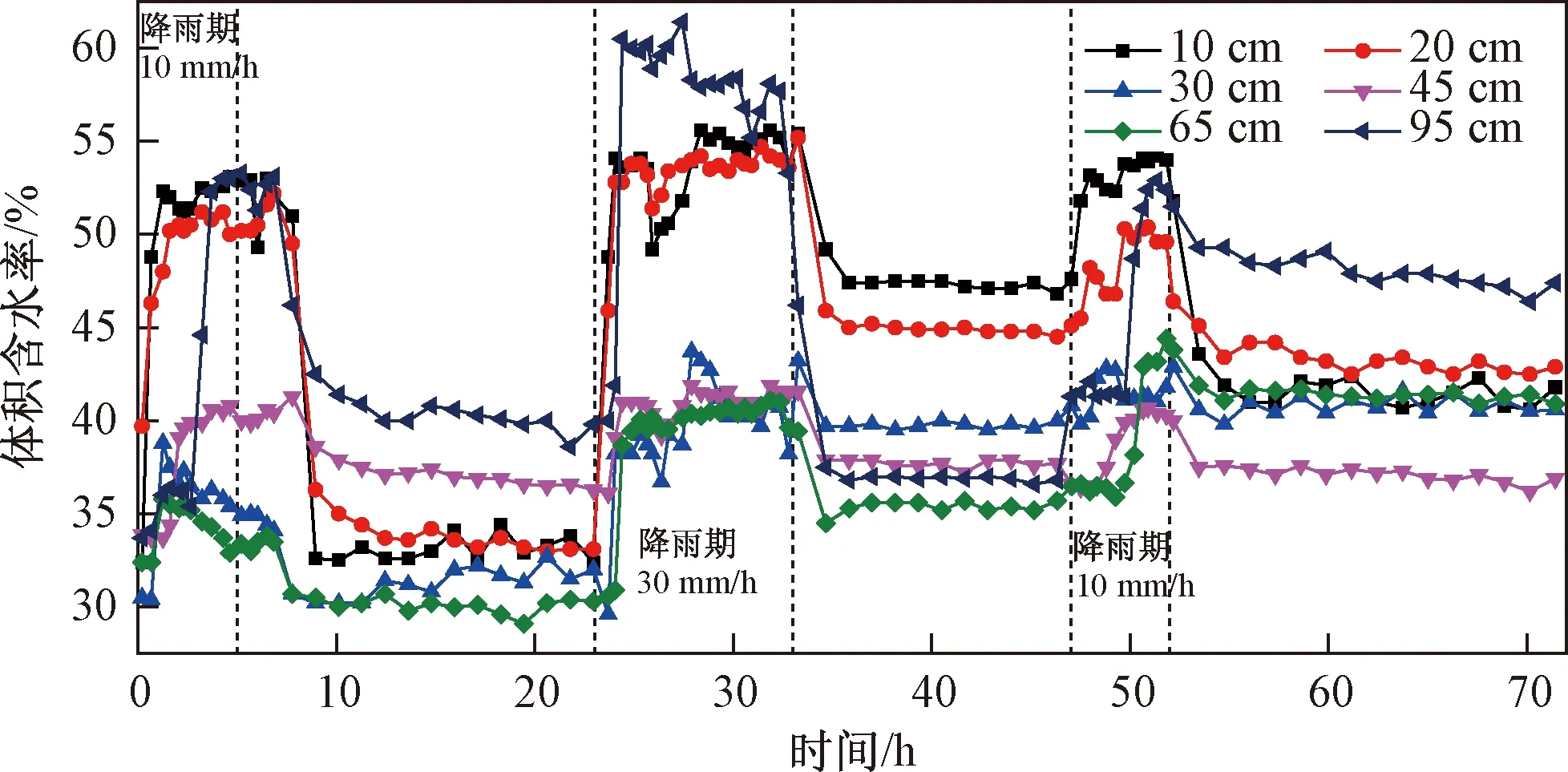
图4 ABA型降雨工况下不同深度土体体积含水率分布Fig.4 Distribution of VWC at different depths in soil column under the central rainfall condition
BAA型降雨工况下,第一天峰值降雨期间各深度体积含水率最大,第三天降雨期大于第二天;降雨间歇期内土柱的体积含水率随着降雨天数的增加逐渐减小,第一天间歇期最大,第三天间歇期最小。土柱内10,20,30,45,65,95 cm深度的初始体积含水率分别为32%、35%、37%、35%、32%、28%。第一天降雨1 h内,土柱内土体的体积含水率从上到下依次增大,10,20,30,65 cm深度增大18%~20%,45 cm深度增大10%,95 cm深度增大27%;降雨结束后,10,20,30,95 cm深度体积含水率降低10%,45,65 cm深度降低5%。第二天降雨2.5 h内,各深度土体从上到下依次迅速增大,10,20 cm深度增大 10%,30,45,65 cm深度增大 5%,95 cm深度增大7%;第二天降雨结束后,土柱内各深度的体积含水率迅速下降,10 cm深度降低7%,20,30,45 cm深度降低5%,65 cm深度降低7%,95 cm深度降低10%。第三天降雨2 h内,从上到下各深度土体的体积含水率依次增大,10,20,30 cm深度增长5%,65,95 cm深度增长10%;第三天降雨结束后,10,20,30,45,95 cm深度降低5%,65 cm深度降低8%。
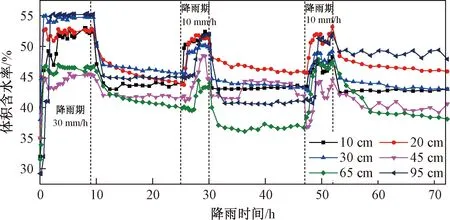
图5 BAA型降雨工况下体积含水率分布Fig.5 Distribution of VWC at different depths in soil column under the advanced rainfall condition
整体来看,马济头滑坡玄武岩残积土上部土体的体积含水率增长速率及幅度较大,浅部及深部土体更易达到饱和;且雨水在峰值降雨期间下渗速率十分迅速。
2.2.3湿润锋运移特征
本次实验中,当土柱内某深度体积含水率持续增大且超过3%时,认为是湿润锋到达该处的时刻。分别绘制湿润锋深度随时间变化的曲线和湿润锋运移速率随深度变化的曲线(图6)。
10 mm/h降雨强度期间,2个土柱的湿润锋下渗深度与时间均呈线性关系,ABA型降雨工况下下渗速率为8.33×10-5m/s,BAA型降雨工况下下渗速率为9.15×10-5m/s。
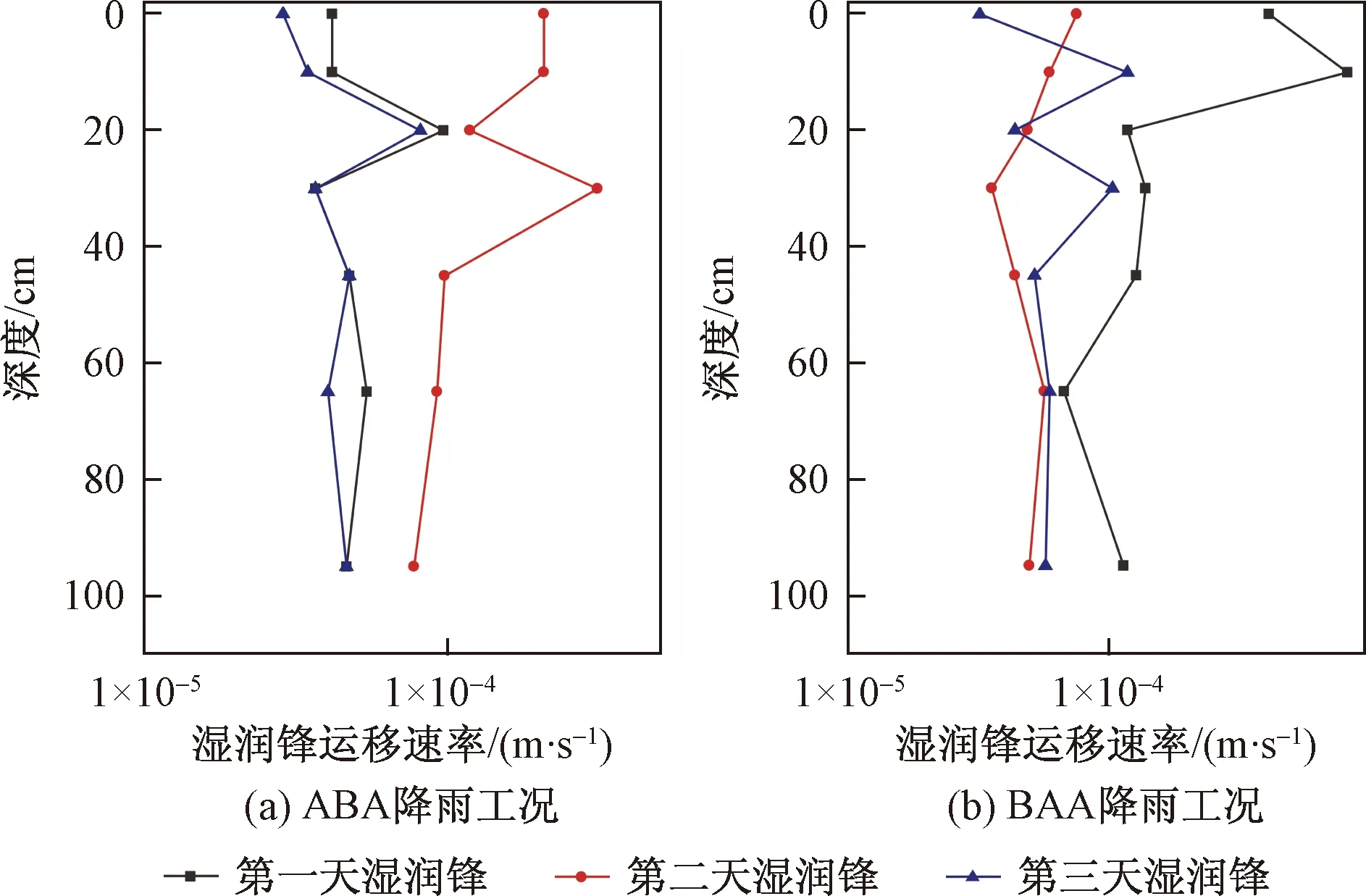
图6 湿润锋向下运移速率曲线Fig.6 Velocity curves of wetting fronts
30 mm/h降雨强度期间,湿润锋运移速率远大于10 mm/h降雨期,且湿润锋随着深度增加速率不断降低。ABA型降雨工的峰值降雨期间,5 cm深度的下渗速率为3.1×10-4m/s,95 cm深度降低75%至7.8×10-5m/s;BAA型降雨工况下的峰值降雨期间,5 cm深度的下渗速率为4.2×10-4m/s,95 cm深度降低85%至6.7×10-5m/s。由此可知,BAA型工况下的峰值降雨期间,随着深度的增加湿润锋运移速率降低的幅度更大。
ABA型降雨工况下的峰值降雨期间,土柱内的平均下渗速率约2.4×10-4m/s,是10 mm/h降雨强度期间的2.9倍;BAA型降雨工况下峰值降雨期间,土柱内的平均下渗速率约2.0×10-4m/s,是10 mm/h降雨强度期间的2倍。以上表明降雨强度增大时,ABA型降雨工况下湿润锋下渗速率的增加幅度更大。
由以上分析可知,马济头滑坡玄武岩残积土土柱内,湿润锋在30 mm/h降雨峰值期间的入渗速率远大于10 mm/h降雨期间,雨水在峰值降雨期间快速进入土柱;峰值降雨期间,ABA型降雨工况下的湿润锋平均速率大于BAA型,且前者随着深度增加速率降低地更慢,更利于雨水入渗。
3 土柱数值模拟
利用数值模拟反演上述土柱实验,以获取玄武岩残积土的土水特征曲线及渗透系数函数。
3.1 渗流基本理论
在SEEP/W中,二维渗流控制方程如下:
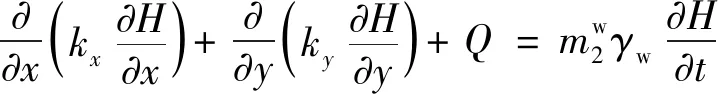
(1)
式中:H——压力水头;
kx、ky——渗透系数,在非饱和土中会随着基质吸力的变化而变化,即由渗透系数函数来定义;
Q——边界流量;

γw——水的重度。
在SEEP/W中进行渗流数值模拟时需要土水特征曲线及非饱和渗透系数函数。本次研究使用Van Genuchten[15]提出的模型来描述土水特征曲线及渗透系数函数。其中,土水特征曲线见式(2)。

(2)
非饱和渗透系数曲线见式(3)。
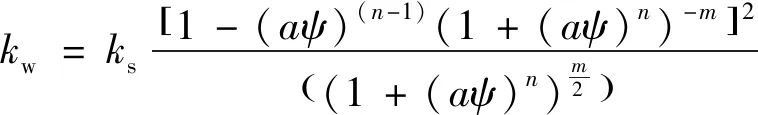
(3)
式中:θs——饱和含水率;
n——曲线基质吸力大于进气值处斜率相关的拟合参数;
a——与进气值有关的拟合参数;

θr——残余体积含水率。
3.2 参数反演方法
式(2)、(3)中的饱和体积含水率和饱和渗透系数ks由室内试验可知为0.60和8.0×10-5m/s。残余体积含水率取经验值为0.085[15]。要得到马济头玄武岩残积土的土水特征曲线和渗透系数曲线,仅需反演得到a、n即可。首先预设a、n的取值范围,并将其等分。根据经验值,我们设定a的取值范围为0.005~0.050,n的取值范围为0.5~5.0,分别等分为15个值,并交叉取值,共有225种组合。在SEEP/W模块中,利用上述225组a、n值得到的土水特征曲线和渗透系数曲线进行土柱降雨入渗数值模拟。计算数值模拟所得体积含水率与物理实验所得结果的均方根误差(RMSE),选取误差最小的一组所对应的a、n值作为反演结果。RMSE的公式见式(4)。
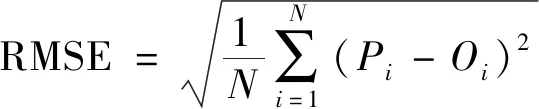
(4)
其中,N为样本的总数量,Pi和Qi分别为模拟值与试验观察值,这里为体积含水率数据。
3.3 土柱降雨入渗数值模拟
本次降雨入渗土柱数值模拟根据物理实验建立数值模型,尺寸为 30 cm×130 cm。上部边界条件为降雨入渗边界,采用的降雨曲线与室内土柱实验相同。侧边界和底边界分别为隔水和自由排水边界。将实验前获取的初始孔隙水压力剖面作为数值模拟中的初始条件。模拟总时长为3 d,步时10 min,共432步。
经过225次模拟,当玄武岩残积土的a、n值分别为0.030,3.0时,用其得到的土水特征曲线和渗透系数曲线进行土柱数值模拟与物理实验结果之间的RMSE值最小。ABA型和BAA型降雨工况下两者之间的RMSE值分别为3.66和4.02。反演所得玄武岩残积土的土水特征曲线与渗透系数函数曲线图7。

图7 玄武岩残积土的土水特征曲线和渗透系数曲线Fig.7 SWCC and hydraulic conductivity function of the basalt residual soils
4 马济头滑坡数值模拟
利用上述反演所得的玄武岩残积土的土水特征曲线和非饱和渗透系数曲线,首先在Geo-studio软件中的SEEP/W模块中模拟得到ABA型和BAA型两种降雨工况下的渗流场,然后将渗流结果耦合到稳定性分析中,得到滑坡的稳定性系数。
数值计算采用的渗流控制方程见式(1)。饱和-非饱和土抗剪强度理论方程采用Fredlund等[17]提出的双变量模型,见式(5)。
τf=c′+(σ-μα)tanφ′+(μα-μw)tanφb
(5)
式中:μα-μw——吸力;
φb——受吸力影响的非饱和土抗剪强度参数;
c′与φ′——饱和土的抗剪强度指标:
τf——剪切破坏面的剪应力。
4.1 数值模型
根据图2所示的马济头滑坡原始斜坡的地质剖面建立其数值模型(图8)。初始的地下水位线由勘察资料获取。为了研究降雨停止后斜坡内渗流场和稳定性的变化,本次模拟的总时长为7 d,包括降雨期3 d,降雨结束后4 d,步时为1 min,步数为168步。
模型中包括玄武岩残积土层及其基岩,两种材料的水文及物理力学参数见表1。数值模型的边界条件设置如下:①模型两侧地下水位以上为零流量边界,地下水位以下为定水头边界;②底边界为不透水边界;③斜坡表面为降雨入渗边界,前3天降雨情况与土柱实验相同(降雨边界不允许积水),后4天为零流量边界。

表1 模型中两种材料的水文和物理参数Table 1 Hydrological and physico-mechanical parameters of two materials in the numerical model
滑面的前、中、后位置布置c、b、a三个监测点(图8),监测滑带土的饱和度及孔隙水压力的变化。

图8 马济头滑坡数值模型Fig.8 Numerical model of the Majitou landslide
4.2 结果分析
4.2.1饱和度及孔隙水压力
图9是在ABA和BAA型降雨工况下,滑面a、b、c三点的土体饱和度变化曲线。
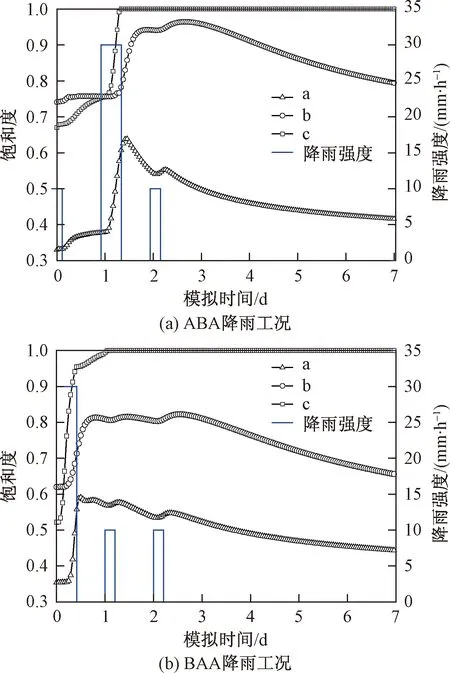
图9 饱和度变化曲线Fig.9 Curves of saturation
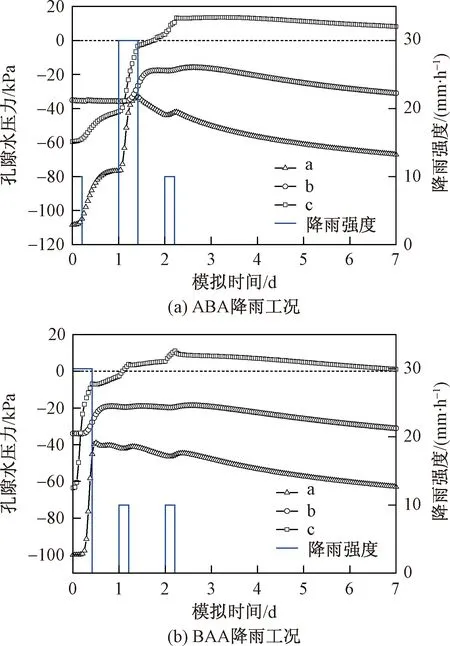
图10 孔隙水压力变化曲线Fig.10 Curves of pore-water pressure
由图9(a)可知,ABA型降雨工况下,第一天降雨5 h后,滑面各点的土体饱和度逐渐增大,但增长幅度仅为0.05~0.1。第二天峰值降雨期,各点饱和度迅速上升,a点由0.35增大至0.65,b点由0.67增大至0.90,c点由0.72增大至完全饱和。峰值降雨结束后,a点的饱和度逐渐降低,第三天降雨期间有小幅回升,随后持续下降,第七天降至0.45;b点饱和度在峰值降雨结束后继续增大,第三天降雨期间增至0.98,几乎饱和,随后逐渐下降,第七天降至0.8;c点饱和度在峰值降雨结束一直饱和直到模拟结束。
由图9(b)可知,BAA型降雨工况下,第一天峰值降雨期间,滑面各点土体饱和度迅速增长,c点可达饱和,b点增大至0.8,a点增大至0.6。峰值降雨结束后,c点保持饱和直到模拟结束;b点在第二和第三天降雨期间分别有小幅度增长,第三天降雨结束后,逐渐降至0.65;a点的饱和度在峰值降雨结束总体呈不断下降趋势,第二天及第三天降雨期有小幅度回升,第三天降雨结束后,逐渐降至0.45。
图10是在ABA型和BAA型降雨工况下,滑面a、b、c三个位置的孔隙水压力变化曲线。由图可知,孔隙水压力的变化规律与饱和度几乎一致。
4.2.2渗流场
图11是在两种降雨工况下,滑坡在稳定性系数最小时步(第58时步)的渗流场。斜坡渗流场内存在3条地下水位线,下部是坡体的原始地下水位线,在降雨过程中始终没有变化;滑面上部的地下水位线呈圈闭状,是由降雨导致的坡体局部滞水,且ABA型工况下的滞水面积比BAA型工况下要大。
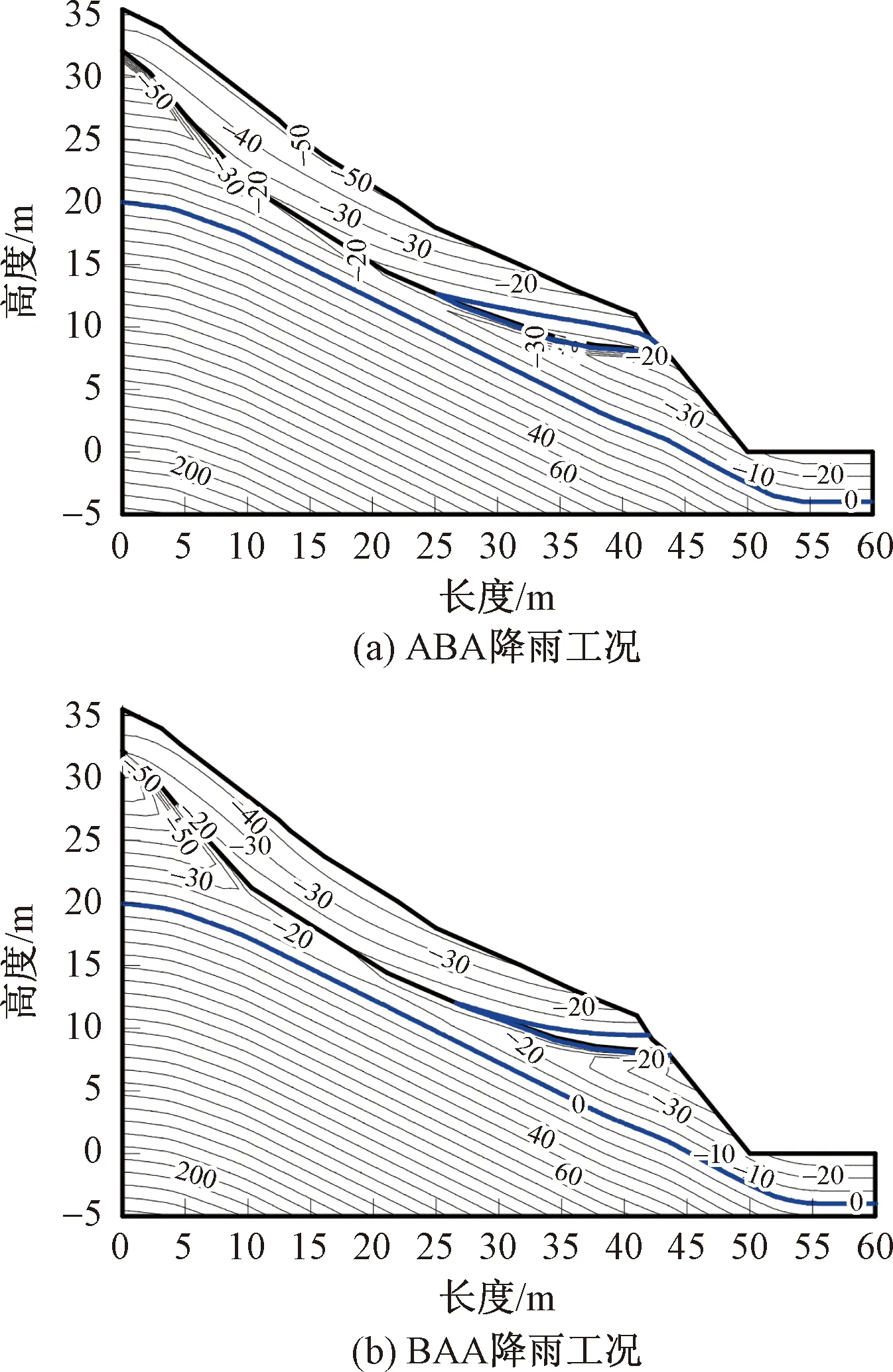
图11 第58时步时斜坡孔隙水压力分布Fig.11 Distribution of pore-water pressures at 58th step
由以上分析可知,由于马济头玄武岩残积土土体松散,渗透性较好,在模拟的两种工况的峰值降雨期间,滑带土的饱和度和孔隙水压力迅速增大,坡脚处形成大面积滞水。且ABA型降雨工况下滑带土的饱和度、孔隙水压力的值以及坡脚滞水面积均比BAA型大。
4.2.3滑面抗剪强度
图12是ABA和BAA型降雨工况下,初始及滑体稳定性系数最小时(第58时步)滑带土的抗剪强度。受降雨入渗的影响,滑带土的抗剪强度有较大程度的降低,特别是在坡肩和坡脚的位置。滑面中部与坡脚处的土体初始抗剪强度分别约40,30 kPa,在模拟的第58时步,滑面中部土体的抗剪强度降至30 kPa,坡肩处的滑面土体抗剪强度降至17 kPa,坡脚处由于局部滞水存在,可降至15 kPa左右。
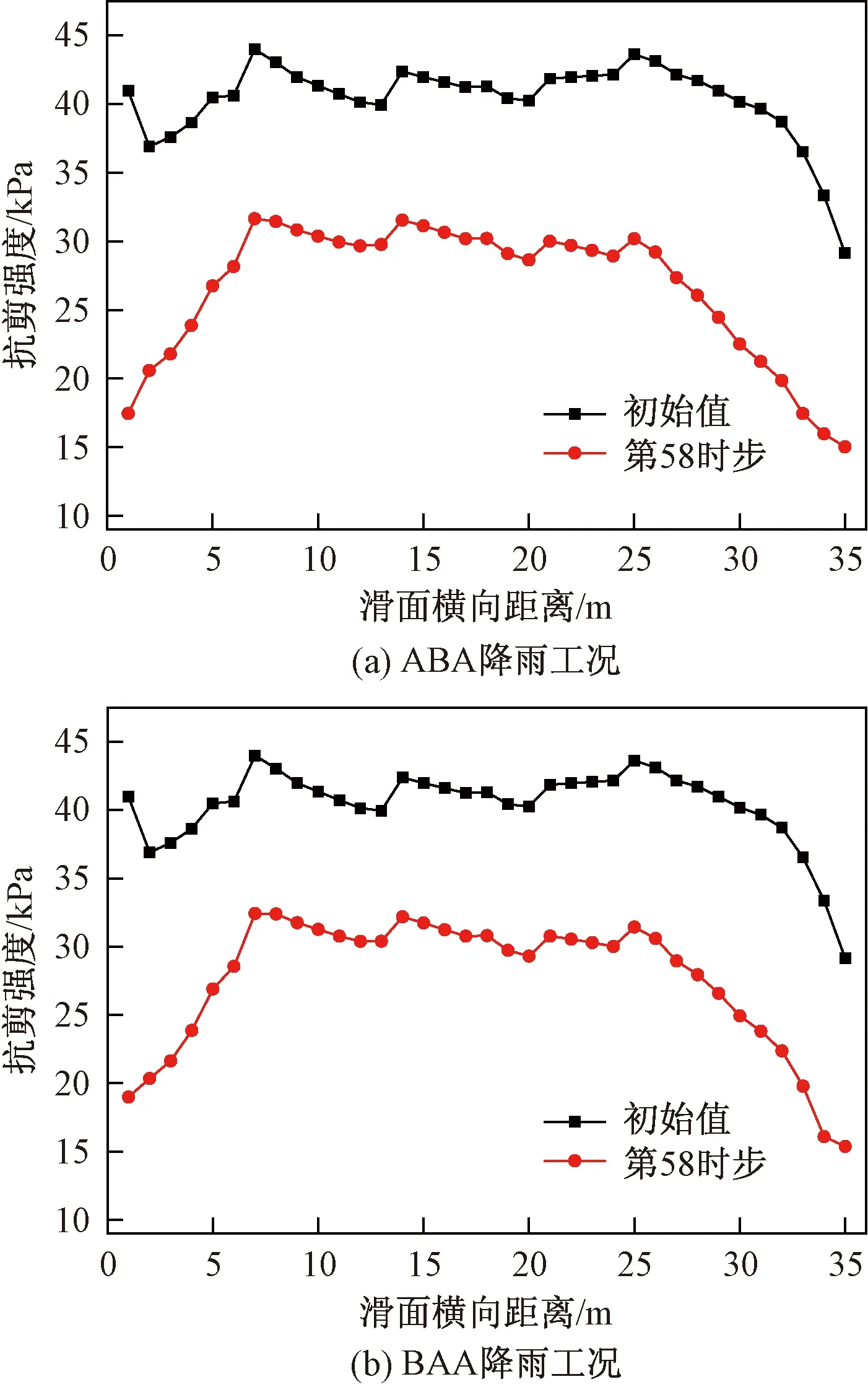
图12 滑面土体抗剪强度Fig.12 Curves of shear strength of the sliding surface
4.3 滑坡失稳机制分析
图13是模拟7 d时间内,滑坡稳定性系数变化曲线。坡体的初始稳定系数为1.375,处于稳定状态,模拟降雨开始后,稳定性系数逐渐降低,且在降雨期明显比间歇降低速率要快。10 mm/h降雨期,稳定性系数下降速率较慢,而峰值降雨期,稳定性系数迅速降低,两种工况均在第三天降雨开始的第10小时(第58时步)稳定性系数降至最低,前峰型工况为1.02,中峰型降雨工况下为0.985。降雨结束后,滑面处的土体饱和度逐渐降低(图9),孔隙水压力随之不断降低(图10),滑坡的稳定性系数随着模拟时间呈线性增大,模拟第七天时,ABA和BAA型降雨工况下滑坡的稳定性系数分别增大至1.13和1.08。
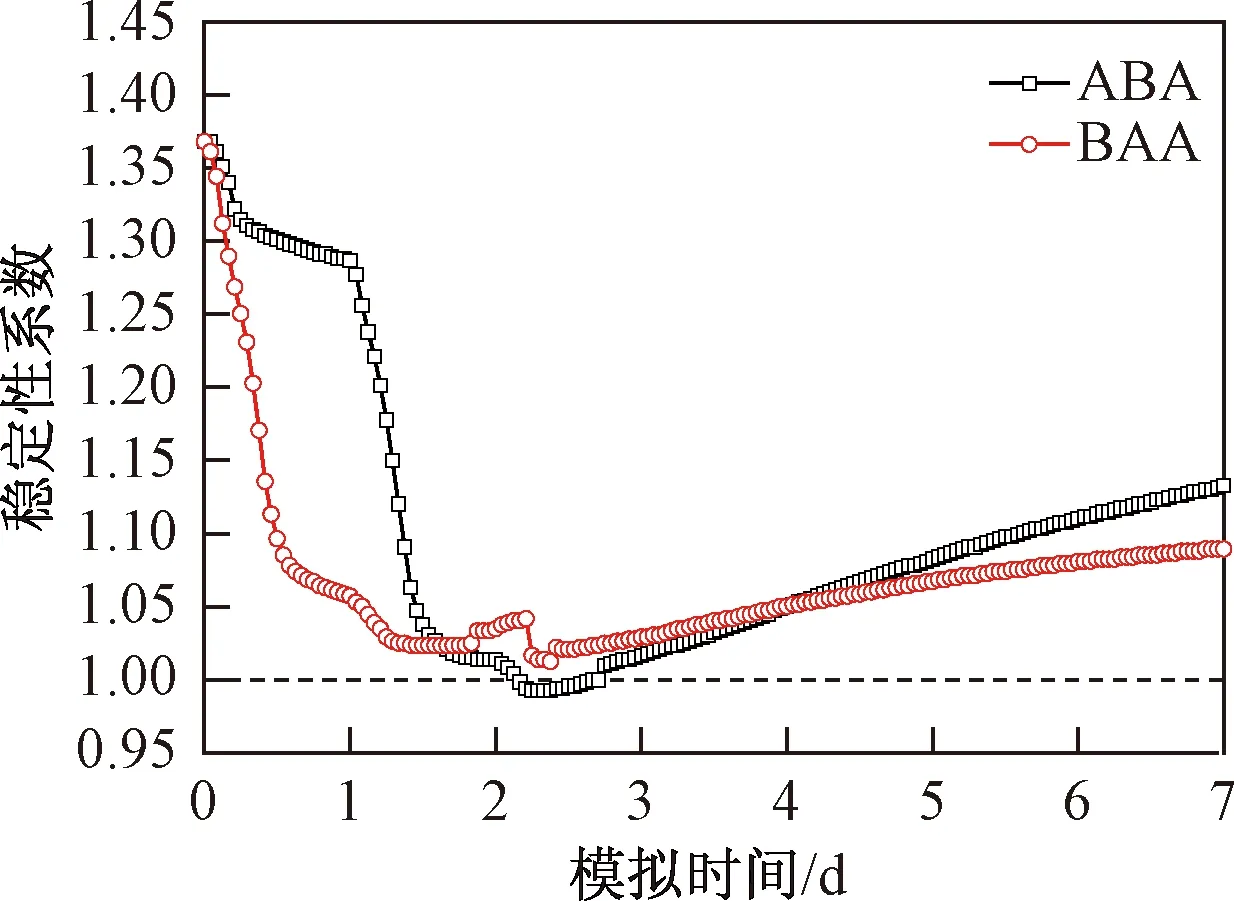
图13 稳定性系数变化Fig.13 Curves of the stability factor
通过土柱实验及数值模拟的分析可知,在ABA和BAA两种降雨工况下,10 mm/h降雨期间,玄武岩残积土的雨水运移速率较小,土体的饱和度,孔隙水压力增长速率较慢,而在峰值降雨期间,雨水运移速率可达10 mm/h期间的2~3倍,滑带土迅速饱和,孔隙水压力迅速增大,坡脚出现大面积的滞水,土体抗剪强度急剧降低。降雨第三天,滑坡的稳定性系数降至最低,滑坡最终失稳。比较ABA和BAA型降雨工况,前者的峰值降雨期间雨水运移速率更快,滑面土体的饱和度增长更快,坡脚处的局部滞水面积也更大,滑坡的稳定性系数更小。因此,中峰降雨工况下,滑坡更容易失稳。
5 结论
(1)降雨作用下,玄武岩残积土土柱的浅层土体含水率增长速率较快,上部及深部土体更易达到饱和。
(2)10 mm/h降雨期间,玄武岩残积土内湿润锋下渗速率较小且不随深度变化;30 mm/h降雨期间,湿润锋下渗速率可增大2~3倍,且随深度的增加下渗速率逐渐减小,雨水主要通过峰值降雨期快速入渗。
(3)降雨作用下,马济头滑坡的滑带土迅速增大,孔隙水压力随之增大,坡脚出现大面积的滞水,土体抗剪强度急剧降低;模拟降雨第三天,滑坡的稳定性系数降至最低,滑坡最终失稳。
(4)中峰型降雨工况下雨水渗入滑坡体的速率更快,滑带土的饱和度增长更快,坡脚处产生更大滞水面积滑坡更容易失稳。
