基于用户查询与样本间匹配度评估的分层抽样策略

邬志罡 荆一楠 何震瀛 王晓阳,3

1(复旦大学计算机科学技术学院 上海 201203)2(上海市数据科学重点实验室(复旦大学) 上海 200433)3(上海智能电子与系统研究院 上海 200433)

0 引 言

在数据探索性分析场景下，用户将发起一系列查询来探索数据集中的海量数据。然而，对整个海量数据集进行完整扫描将导致用户查询缓慢且阻碍了系统交互性，严重影响了用户的生产力甚至创造力[1]。因此，用户通常借助抽样系统来生成海量数据集上的一个样本子集，并在样本集上得到查询的近似结果，以查询结果精确度上的损失换取更快的查询速度。

分组聚合查询普遍存在于数据探索性分析场景中，例如当用户在保存商品交易记录的数据集上进行探索时，将会发起如下查询：SELECT SUM(sales) FROM order GROUP BY type来分析各种种类的商品销售情况。在这种情况下，如果在构造样本时采用随机均匀抽样策略(Uniform Sampling)，那么生成的样本集中每种商品种类的样本量将正比于该商品种类的交易记录数量。这种均匀抽样策略将导致从小众的商品类别分组中收集到的样本量不足，甚至导致交易数量非常稀缺的商品类别分组完全消失在最终结果中，从而产生很大的误差[2]。为了能在相同抽样率的限制条件下使得查询结果拥有更高的精确度，现有系统通常采用分层抽样策略(Stratified Sampling)[3]，即首先按照分组属性的取值对数据集进行划分，进而在划分出的每个分组中进行抽样。例如在上述的示例中，首先按照商品种类type对数据集进行分类，然后对每一类商品种类type中的数据分别进行抽样。设计一种有效的分层抽样策略的关键在于：(1) 依据哪些属性进行分层；(2) 如何将固定的总样本量具体分配到每一层中。针对第一个问题，现有分层抽样系统通常利用到了用户的历史查询记录。此类系统基于用户的历史查询记录能被用来较为精准地预测未来用户查询请求这一假设，针对用户历史查询记录中表现出的分组特征，筛选出频率最高的几组分组属性列集合，然后在其上进行分层抽样。然而，在现实场景中，当用户查询特征的稳定性无法得到保证时，或是在用户查询历史无法获得的情况下，甚至是当抽样系统冷启动未运行任何查询时，现有的用户查询历史驱动的抽样系统将无法达到预期的效果。另一方面，针对上述第二个问题，国会抽样策略[4]一文中给出了当查询中分组条件确定时，最优的分层抽样策略对应的总样本量具体到每个分组的分配方案，即在各分组间完全均匀分配。基于这一理论，该文作者进一步提出了国会抽样策略，即一种总样本量分配方案优化后的分层抽样策略。然而，该抽样策略虽然生成了一个面对任何分组查询时能够取得较优的平均效果的样本集，但其仅给出了在数据集上生成唯一一份样本集的抽样策略。然而，在现实场景中，如果抽样系统能够为用户生成多份离线样本集并支持在运行时自动从其中为用户选择出最匹配当前查询的样本集，其效果显然要好于用一份样本集来应对所有可能的用户查询[5]。

面对上文提到的这些挑战，本文提出一种新的抽样策略。本文主要贡献包括：(1) 为任一具体分层抽样策略，即其所生成的样本集，与任意分组聚合查询提供了一种匹配度评估的方法，并且提供了根据匹配度评估打分为用户查询选取最优样本集的方法。(2) 提出了一种基于用户查询与样本间匹配度评估的分层抽样策略，支持离线生成包含多份分层抽样样本集的抽样组合。(3) 以限定相同样本量评估近似结果精确度的方式，通过在模拟数据集和真实数据集上的大量实验证明了本文提出的抽样策略的有效性。

1 相关工作

BlinkDB[6]通过分析用户的历史查询记录，在筛选出的若干个热点分组属性集上进行分层抽样。当用户的历史查询记录能很好地表征未来的查询情况时，这种针对特定的查询特征生成的特定抽样策略显然能够获得不错的效果。然而，在某些数据探索性分析场景下，由于不同用户的探索目的各不相同且其探索意图随时间不断改变，这种用户查询特征不随时间变化的稳定性假设通常无法得到保证，因此此类抽样系统的效果也会受到很大影响。另一方面，BlinkDB需要在运行时从多份预先准备的离线样本中选取出一份最适合当前查询的样本，其选择方法仅仅考虑了当前分组聚合查询的分组条件属性集与某一离线分层抽样策略的分层属性集之间的集合包含关系，没有给出一个具体的可供量化的评估标准。

ICICLES[7]在进行抽样时，对数据集中的每条记录的抽取概率正比于该条记录累计出现在用户历史查询产生的结果集中的次数。该系统不断更新维护一个根据用户历史查询生成的多重集合，即一种允许相同元素重复出现的集合。每条用户查询结果中涉及到的数据记录都会被存放在这个多重集合中。该系统将会在该多重集合上进行随机均匀抽样，以期望生成的样本集能匹配将来的用户查询。然而，这样的方式不仅使其生成的样本强依赖于用户历史查询记录，并且会使得那些还没有被用户探索到的区域样本量极其匮乏，这将严重阻碍用户探索数据集中新的区域以获取新的发现或结论。

国会抽样策略[4]通过优化分层抽样策略的总样本量分配方式来提高针对用户分组聚合查询返回的近似结果的精确度。相较于其仅仅生成唯一一份样本集，本文提出的抽样策略可以支持生成多份离线样本集并在运行时自动从多份离线样本集中选出最匹配的一份样本集进行近似结果计算。由于准备了多份离线样本，从中选出一份更能匹配当前用户查询特征的样本的可能性将大大提升。

2 问题归纳

分层抽样策略是一种先将整个数据集按照某些属性上的取值分成若干层，然后再从每一层中随机抽取样本的抽样方法。分层抽样策略中，如何将总样本量具体分配到每个分组中是影响最终生成的样本集效果的最主要的问题。幸运的是，关于分层抽样策略的诸多特性已经有多位学者进行了研究总结。Acharya[4]证明了针对某一特定的用户分组聚合查询，即当用户查询中的分组条件确定时，最优的分层抽样总样本量分配方案就是在该分组查询将会产生的所有分组间均匀分配样本空间。

从上文提到的分层抽样策略最优总样本量分配方案中，我们可以看出，包含不同分组条件组合的用户查询所对应的最优样本集都是不同的。因此，抽样系统希望通过仅仅一份离线样本去应对所有可能的用户查询并都能获得较优的效果的这一目标是不现实的。如果系统可以在离线时生成多份样本集，并且能够在运行时自动根据当前用户分组聚合查询取出一份最匹配的样本集进行近似结果计算，那么系统将有更大机会得到更为精确的近似结果。然而，在应对实际场景时，我们显然无法为用户发起的每种可能的分组聚合查询准备一份最优样本。试想，当用户的查询模式不具备时间上的稳定性时，我们想要优化的查询集合将无法被缩小到一个预处理开销可以承受的范围内。例如，当数据集上共有20个分组属性时，总共会产生220种分组条件组合情况。如果我们希望能在运行时为任一可能的用户查询都匹配到最优的离线样本集，那么我们在预处理阶段需要对每种可能的分组条件组合都预先保存一份分层抽样样本。即使每份样本集的抽样率仅为0.1%，那么总的预生成样本集合的数据量大小也将会超过原始数据集的1 000倍。本文中，我们将考虑更为实际的应用场景，即用户可提供的用于生成离线样本集的存储空间是有限的。因此，本文提出的抽样系统的设计目标可具体定义为：针对某一特定的数据集，如何生成k份分层抽样样本集，使得在运行时能从k份样本集中挑选出最合适的一份，从而期望能在所有可能的用户分组查询上的平均误差达到最小值。

3 基于匹配度评估的分层抽样策略

3.1 抽样策略间的匹配度评估

上节中，我们已经阐述了用户发起的每一类分组聚合查询都具有相对应且确定的最优分层抽样总样本量分配方案这一理论基础。并且，任意样本集都能根据其在每个分层上保存的样本点个数回溯到一个具体的分层抽样总样本量分配方案。那么，如果我们能够为分层抽样策略任意两种总样本量分配方案间提供一种匹配度评估的方法，我们就能将任意用户查询与样本集之间的匹配度评估转换为该用户查询对应的最优抽样策略与生成该样本集的具体抽样策略这两种不同的分层抽样总样本量分配方案之间的匹配度评估。我们也就能将上节中提出的实际场景下的抽样系统设计目标形式化地定义为一个优化问题。该优化问题的损失函数即为使用k份离线样本集来应对所有可能的用户分组查询时将会产生的匹配度损失的总和。接下来，本节将先介绍任意分层抽样总样本量分配方案的形式化表示公式并进一步提出任意两种抽样策略间匹配度损失的形式化评估方法。

考虑某数据集D，可用作用户查询分组条件的类别分组属性为A1,A2,…,Aα。其中，又有每个类别所对应的值域上取值的数量大小为N1,N2,…,Nα。那么用户在该数据集上发起的分组聚合查询所产生的最小分组单位g的总数量为N1×N2×…×Nα。例如，考虑包含某国人口调查数据的数据集，其中共有两个分组属性A1和A2，分组属性A1为性别，分组属性A2为学历。考虑每种分组属性值域上取值的数量，分组属性A1对应的取值可能为“男性”或“女性”，即N1为2，分组属性A2对应的取值可能为“本科”、“硕士”或“博士”，即N2为3。那么，总共将产生6个最小分组单位gi(1≤i≤6)，分别为：g1:(“男性”，“本科”)、g2:(“男性”，“硕士”)、g3:(“男性”，“博士”)、g4:(“女性”，“本科”)、g5:(“女性”，“硕士”)、g6:(“女性”，“博士”)。

定义一种离散概率分布，其在任意最小分组单位g上的概率取值为p(g)，代表从生成的离线样本集中任意取出一条记录，该记录属于最小分组单位g的概率。那么有：

式中：S为总抽样数量大小，Sg为总抽样数量S分配到最小分组单位g上的抽样数量大小，且∑p(g)=1。由此，我们可以将任意分层抽样策略总样本量分配方案转化为离散概率分布的形式。至此，我们得以通过衡量两个离散概率分布间差异的距离函数，正式定量地评估任一总样本量分配方案与用户分组聚合查询确定下的最优样本量分配方案间的匹配度损失程度。本文选取Jensen-Shannon散度[8]来衡量两种抽样策略间的匹配度损失程度。对于在同一值域Y上的概率分布P和Q，Jensen-Shannon散度定义如下：

式中：M定义如下：

公式中的KL是Kullback-Leibler散度[9]，是一种可用来测量两组概率分布间差异性的非对称性指标，定义如下：

当两个概率分布相同时JS取值为0，两个概率分布间的匹配度损失越大，则JS取值也将会增大。

3.2 抽样策略的设计与实现

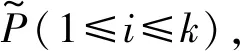
式中：U代表在该数据集上用户发起的分组聚合查询中，所有可能的分组条件组合的集合。PU代表的是，依据Acharya证明的分层抽样总样本量分配方案理论[4]所得到的最优抽样策略对应的概率分布。

为了解决上述优化问题，我们设计了一种自适应的优化算法，该算法基于优化问题中的一种经典随机爬山算法(Stochastic Hill Climbing)[10]。该算法的主要流程如算法1所示。

算法1生成包含k组概率分布的最优解集

输入:迭代次数阈值tIteration，优化目标损失值阈值tError

输出:包含k组概率分布的最优解集：solutionSet

1: solutionSet←insertkinitial probability distributions

2:t:iteration times←0

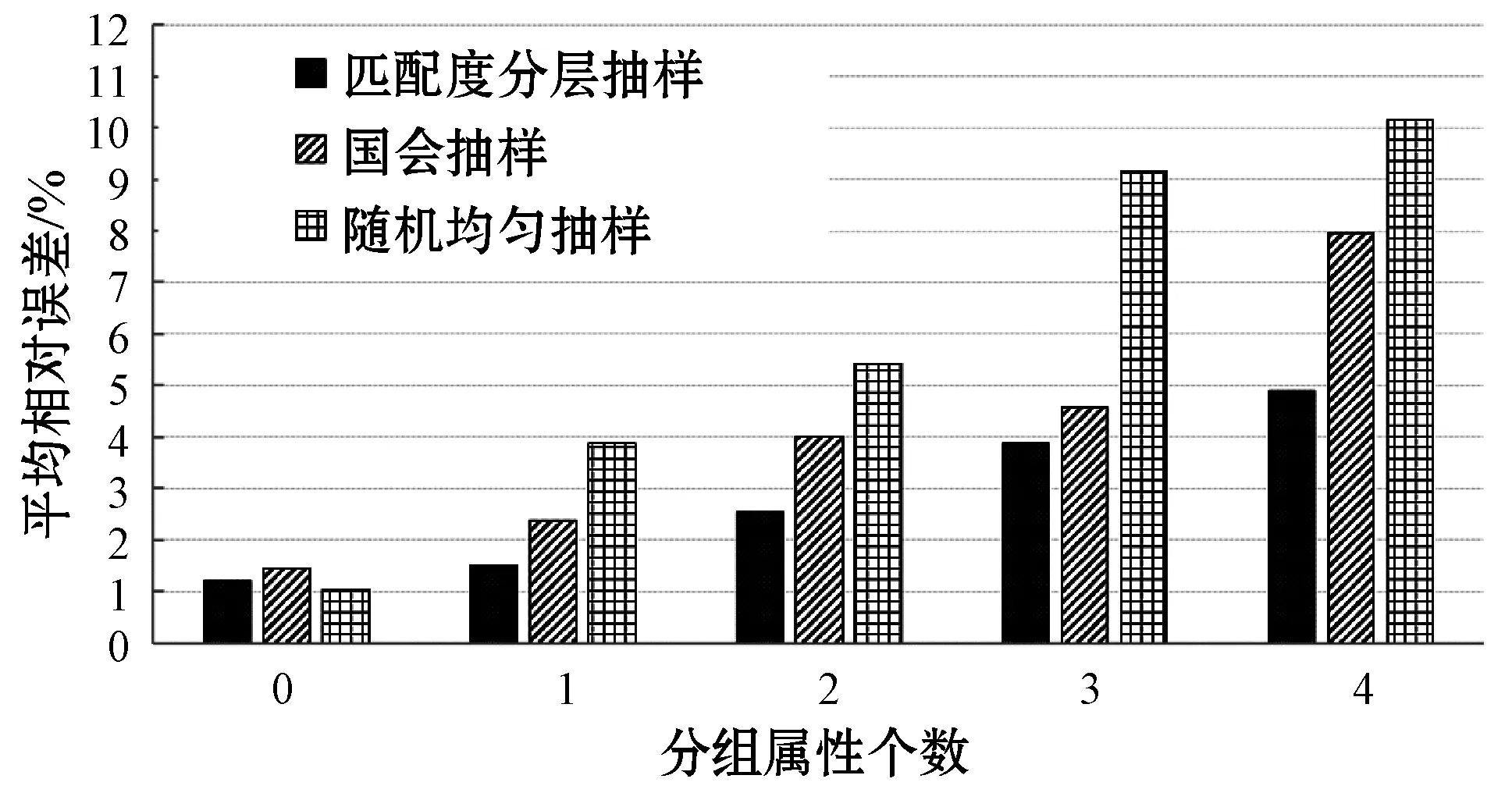
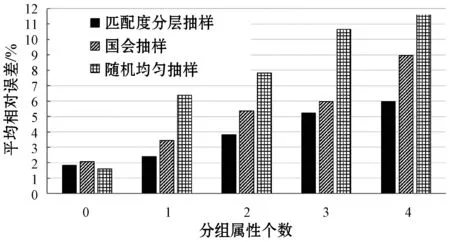
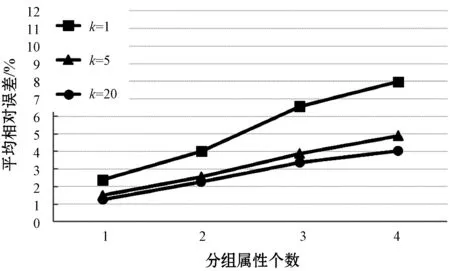
3:whileLOSS(solutionSet)>tErrorANDt

4: Generate solutionSetNew based on solutionSet

5:ifLOSS(solutionSetNew)

6: solutionSet←solutionSetNew

7:endif

8:t←t+1

9:endwhile

10:returnsolutionSet

在算法1中，主要包含了如下三个关键步骤:

(1) 第1行。在算法的初始化阶段，我们为k组抽样策略，即为其分别对应的k个概率分布选择k组合适的初始解集。

(2) 第4～7行。每轮迭代产生一组新的解集，并重新评估新的解集在优化目标查询集合上的损失值。若新的解集相比于当前解集能够使得系统总优化目标的损失值降低，则保留新的解集作为当前解集，反之则丢弃。

(3) 第3行。当系统总优化目标损失值低于阈值tError时，或当迭代次数大于阈值tIteration时，终止算法。否则，重复执行步骤(2)。

其中，损失函数定义如下：

对于步骤(1)，一个合适的初始解集可以帮助优化算法更快地终止。虽然随机均匀抽样策略在面对用户分组聚合查询时不是最优解，但其得到的样本保留了数据集原始的数据分布特征，并且是应对非分组查询时的最优抽样策略。因此，在没有任何额外信息的情况下，为了避免生成更糟糕的初始解集，我们就将随机均匀抽样策略选做初始解集。对于步骤(2)，由于我们已经明确定义了系统的总体优化目标，因此可以直接使用总体目标的衡量公式来对生成的中间解进行效果评估。在生成新的解集时，每个分组增大或减小样本空间的概率将反比于该分组的大小。这是由于近似结果的误差更多来源于样本量更小的分组，调整此类分组使得我们的算法更有可能更快地向接近总体优化目标的方向移动。

本文所述系统将在离线状态下，按照上文所描述的优化算法，生成一组各自代表不同分层抽样策略总样本量分配方案的概率分布。在分布式数据仓库Hive[11]上，本系统将按照概率分布中所指示的各最小分组单位g上的抽样率在各个分组上进行随机均匀抽样，并将生成的样本集保存在数据仓库Hive中。与此同时，系统将会记录下与当前系统中保存的每份离线样本集一一对应的概率分布描述。这些概率分布所代表的各最小分组单位上的抽样率信息将会在系统在线运行时被用来进行与当前用户查询进行匹配度评估，并且用来缩放在样本集上得到的用户查询结果，以生成最终需要返回的近似用户查询结果。

3.3 系统运行时的样本选择与查询重写

至此，本系统在运行时仍有两个问题需要解决：

(1) 当某个具体的用户分组聚合查询请求到来时，系统将如何从离线生成的多份样本集中选取出最优的一份样本，进行近似结果计算。正如3.1节中所述，任意的分层抽样总样本量分配方案可以被转化成一个概率分布。同时，对于每个到来的用户查询，我们都可以相应地通过考虑查询中的分组条件来计算出最匹配该查询的概率分布。由于我们在离线时保存了每份样本集对应的概率分布信息，因此我们有理由从中选出一份与当前用户查询所对应的最优概率分布匹配度最高的样本集进行近似结果计算。唯一需要注意的是，系统在运行时使用的匹配度评估函数应当与系统在离线生成样本集时，运行的优化算法中所使用的匹配度评估函数保持一致。

(2) 由于本系统使用的是分层抽样策略，并且对每个分组的抽样率不同，是一种有偏的抽样方法，因此，系统需要重写用户查询以生成无偏的近似结果。在离线生成样本时，当系统从不同分组中按照抽样率随机均匀抽取不同数量的样本时，系统同时已经为每条样本记录保存了一个缩放因子。由于同一分组中的所有样本记录对应着相同的抽样率，因此同一分组中生成的样本记录将共享相同的缩放因子，即为该样本记录所归属的分组上的抽样率的倒数。在运行时，本系统将利用这些缩放因子来对每条样本记录进行加权处理，以得到无偏近似结果。具体来说，对于求和操作(SUM)，近似结果将会是所有相关的样本记录与相应的缩放因子的乘积的和。对于计数操作(COUNT)，近似结果为所有相关的样本记录对应的缩放因子的和。相应地，求平均值操作(AVG)通过将SUM与COUNT的结果相除计算得出。

4 实 验

4.1 实验设置

本文的实验环境为包含1个master节点和9个slave节点的Spark集群。每一台机器分别搭载主频为2.1 GHz的Intel Xeon E5-2600处理器和64 GB内存，运行在64位Ubuntu 14.04 Server系统上。集群上运行Spark 2.0.0和Hive 1.2.1。

(1) 模拟数据集 我们在TPC-H数据库基准测试数据集[12]上生成模拟数据集及测试查询模板。在原始的TPC-H数据集中，分组的数量及各分组的大小分布都相对较为均匀。为了能更好地模拟出真实情况下的数据集，并且为了能够更好地对比不同抽样策略在应对更具挑战的倾斜数据集时性能上的差异性，我们利用了一个经过版本修改的dbgen工具[13]生成非均匀分布的数据集。该工具将根据Zipf分布生成倾斜数据。在本实验中，Zipf分布的特征指数z被设置为1.5。我们选取了TPC-H数据集中的lineitem表，并将扩展因子设置为100，最终得到了总大小为74.7 GB的模拟数据集。在构造用于实验测试用的模拟用户分组聚合查询时，我们通过随机生成若干分组属性并进行随机组合的方式来生成模拟用户分组聚合查询，以达到模拟测试现实场景中抽样系统应对Ad-Hoc查询时表现出的性能效果。

(2) 真实数据集 我们从公开的斯隆数字巡天数据集SDSS网站[14]上下载了真实数据集和真实的用户查询记录。我们从SDSS数据集的BestDr8版本中选用了PhotoPrimary视图，获取了总共101.45 GB的数据。下载到的用户查询记录被进行了一定修改以使其符合Spark SQL的语法定义。

在整个实验过程中，我们对比了随机均匀抽样策略、国会抽样策略和本文提出的匹配度分层抽样策略。每种策略都在离线时都生成了抽样率为1%的样本。对于匹配度分层抽样策略，默认用户设置的离线样本集个数k为5。

4.2 模拟数据集上精确度的表现

实验一中，我们在模拟数据集TPC-H上总共生成了30条随机用户查询，并且对每条用户查询运行在三种不同的抽样策略生成的样本集上得到的近似结果的相对误差做了统计。我们根据用户查询中分组条件属性的个数将用户查询分为了五类，以便能够更为细致地考察不同抽样策略在分组条件数量不同的情况下的表现。在TPC-H模拟数据集上的实验统计结果如图1所示。

图1 TPC-H数据集上三种抽样策略的平均相对误差

由图1可知，当分组属性个数为0时，代表当前测试用户分组聚合查询为不包含分组条件的非分组查询。由于随机均匀抽样策略完全保留了整个数据集上底层的数据分布特征，因此其在非分组用户查询下的表现自然会优于分层抽样策略。在国会抽样策略中，由于抽样策略更倾向于补偿小的分组因此会破坏整个生成的样本的均匀性，导致其在应对非分组查询时效果不佳，相较均匀抽样策略误差率提高了39.4%。而在本文提出的匹配度抽样策略中，由于非分组用户查询相较于其他分组用户查询的特殊性，其在系统的总优化目标中往往会产生很大影响。因此，在最后生成的多份离线样本集中将会有一份样本倾向于对非分组用户查询更加友好，使得本系统在面对非分组用户查询时也能获得较好的效果。相较于国会抽样策略，针对非分组用户查询，本文提出的匹配度分层抽样策略在平均相对误差上降低了16.6%。

从图中的统计结果可以看出，随着分组属性个数的增长，各系统产生的近似结果的误差也在随之增长。这是由于当分组属性个数增加时，用户查询产生的结果中将包含更多的分组数量并且各分组中包含的记录数量的大小分布也将变得更加不平衡。分层抽样策略在应对这种条件下的用户查询时，效果要显著好于随机均匀抽样策略。而由于本系统通过衡量不同分组查询对应的最优分层抽样总样本量分配方案，将匹配度较高的总样本量分配方案进行聚合，因此可以通过离线保存为数不多的多份样本集的方式，优化绝大部分的分组查询。实验结果也表明，当用户查询中分组属性个数增加时，本系统生成的近似查询结果的误差的增加呈现出放缓的趋势。相比于国会抽样，本文提出的匹配度分层抽样策略在模拟数据集TPC-H上的平均相对误差降低了25.4%。

4.3 真实数据集上精确度的表现

实验二中，我们选取了SDSS真实数据集并下载了真实的用户查询。我们同样对这些真实用户查询按照分组属性个数进行了分类，实验获得的统计结果如图2所示。

图2 SDSS数据集上三种抽样策略的平均相对误差

在真实数据集上，三种抽样策略的表现与我们在模拟数据集上得出的结果非常相似。对于非分组用户查询，相较于国会抽样，本文提出的匹配度分层抽样将近似结果的精确度提高了12.4%。相比于国会抽样，本文提出的匹配度抽样策略在真实数据集SDSS上的平均相对误差降低了26.3%。

4.4 离线样本集个数k的影响

实验三在TPC-H模拟数据集上进一步考察了本文提出的匹配度分层抽样系统中，用户允许存储的离线样本集个数k对于近似结果精确度的影响。图3展示了在不同的k值情况下，用户查询的平均相对误差随分组属性个数的变化情况。从图中可以看出，当k为1时，即系统仅能保存一份离线样本时，本文系统产生的离线样本集将接近于国会抽样策略所生成的样本集，误差较大。而当k不为1时，即用户允许系统保存多份离线样本时，由于系统可以通过数据特征预存多份离线样本并且在运行时选择出一份最优样本进行近似结果计算，其产生的近似结果的精确度相较于仅保存一份离线样本时有着明显提升。另外，可以看到当k值为5时，系统已经能够达到一个较好的性能，说明本文提出的优化算法能够很好地将具有相似数据分布特征的多种用户分组查询经优化后聚合到一份离线样本集中。因此仅仅用少量的离线样本集就能在大量的用户查询上达到较为出色的抽样效果。

图3 离线样本集个数k对用户查询平均误差的影响

5 结 语

本文提出了一种基于用户查询与各分层间总样本量分配方案匹配度评估的分层抽样策略，系统在运行时可以从多份离线样本中选出一份最匹配当前查询的样本进行近似结果计算。同时，本文还为任一分层抽样策略与任意用户分组聚合查询的匹配度提供了一种基于概率分布和数据特征的形式化定量评估方法。通过在模拟数据集和真实数据集上的广泛实验，本文验证了数据驱动的基于匹配度评估的分层抽样策略相较于传统抽样策略在用户查询近似结果的精确度上有了明显提升。