Robust Re-Weighted Multi-View Feature Selection

Yiming Xue,Nan Wang,Yan Niu,Ping Zhong,Shaozhang Niuand Yuntao Song

Abstract: In practical application,many objects are described by multi-view features because multiple views can provide a more informative representation than the single view.When dealing with the multi-view data,the high dimensionality is often an obstacle as it can bring the expensive time consumption and an increased chance of over-fitting.So how to identify the relevant views and features is an important issue.The matrix-based multi-view feature selection that can integrate multiple views to select relevant feature subset has aroused widely concern in recent years.The existing supervised multi-view feature selection methods usually concatenate all views into the long vectors to design the models.However,this concatenation has no physical meaning and indicates that different views play the similar roles for a specific task.In this paper,we propose a robust re-weighted multi-view feature selection method by constructing the penalty term based on the low-dimensional subspaces of each view through the least-absolute criterion.The proposed model can fully consider the complementary property of multiple views and the specificity of each view.It can not only induce robustness to mitigate the impacts of outliers,but also learn the corresponding weights adaptively for different views without any presetting parameter.In the process of optimization,the proposed model can be splitted to several small scale sub-problems.An iterative algorithm based on the iteratively re-weighted least squares is proposed to efficiently solve these sub-problems.Furthermore,the convergence of the iterative algorithm is theoretical analyzed.Extensive comparable experiments with several state-of-the-art feature selection methods verify the effectiveness of the proposed method.

Keywords:Supervised feature selection,multi-view,robustness,re-weighted.

1 Introduction

In many applications,we need to deal with a large number of data which have high dimensionality.Handling high dimensional data(such as image and video data)may bring many challenges,including the added computational complexity and the increased chance of over-fitting.So how to effectively reduce the dimensionality has become an important issue.As an effective method of selecting representative features,feature selection has attracted many attentions.Feature selection methods[Fang,Cai,Sun et al.(2018)]can be grouped into filter methods,wrapper methods,and embedded methods.Filter methods select features according to the general characteristics of data without taking the learning model into consideration.Wrapper methods select features by taking the performance of some model as criterion.Embedded methods incorporate feature selection and classification process into a single optimization problem,which can achieve reasonable computational cost and good classification performance.Thus,embedded methods are in the dominant position in machine learning,and Least absolute shrinkage and selection operator(Lasso)[Tibshirani(2011)]is one of the most important representatives.

Recently,unlike the previous vector-based feature selection methods(such as Lasso)that are only used for binary classification,many of matrix-based structured sparsity-inducing feature selection(SSFS)methods have been proposed to solve multi-class classification[Gui,Sun,Ji et al.(2016)].Obozinski et al.[Obozinski,Taskar and Jordan(2006)]first introducedl2,1-norm regularization term which is an extension ofl1-norm in Lasso for multi-task feature selection.Thel2,1-norm regularizer can obtain a joint sparsity matrix because minimizingl2,1-norm will make the rows of transformation matrix corresponding tothenonessentialfeaturesbecomezerosorclosetozeros.Thankstoitsgoodperformance,many SSFS methods based onl2,1-norm regularizer have been proposed[Yang,Ma,Hauptman et al.(2013);Chen,Zhou and Ye(2011);Wang,Nie,Huang et al.(2011);Wang,Nie,Huang et al.(2011);Jebara(2011)].In addition,Nie et al.[Nie,Huang,Cai et al.(2011)]utilizedl2,1-norm penalty to construct a robust SSFS method called RFS to deal with bioinformatics tasks.Unlike the frequently-used least squared penalty,the residual in RFS is not squared,and thus the outliers have less influence.With the aid ofl2,1-norm penalty,several robust SSFS methods have been proposed[Zhu,Zuo,Zhang et al.(2015);Du,Ma,Li et al.(2017)].

As is known,the description of an object from multiple views is more informative than the one from single view,and a large amount of multi-view data have been collected.In order to describe this kind of data in a better way,a lot of features are extracted by different feature extractors.How to integrate these views to select more relevant feature subset is important for the subsequent classification model.Xiao et al.[Xiao,Sun,He et al.(2013)]firstly proposed the two-view feature selection method.However,many objects are described from more than two views.Wang et al.[Wang,Nie,Huang et al.(2012);Wang,Nie and Huang(2013);Wang,Nie,Huang et al.(2013)]proposed the improved multi-view feature selection methods to handle the general case.In Wang et al.[Wang,Nie and Huang(2012)],they established a multi-view feature selection framework by adoptingG1-norm regularizer andl2,1-norm regularizer to make both views and features sparsity.In Wang et al.[Wang,Nie and Huang(2013);Wang,Nie,Huang et al.(2013)],SSMVFS and SMML were proposed by using the same framework to induce the structured sparsity.Specifically,SSMVFS employed the discriminative K-means loss for clustering,and SMML employed the hinge loss for classification.Zhang et al.[Zhang,Tian,Yang et al.(2014)]proposed a multi-view feature selection method based onG2,1-norm regularizer by incorporating the view-wise structure information.Gui et al.[Gui,Rao,Sun et al.(2014)]proposed a joint feature extraction and feature selection method by considering both complementary property and consistency of different views.

Multi-view feature selection methods have achieved good performance.Concatenating multiple views into new vectors is a common way when establishing the multi-view feature selection schemes.However,the concatenated vectors have no physical meaning,and the concatenation implies that the different views have similar effects on a specific class.In addition,the concatenated vectors are always high dimensional,which increases the chance of over-fitting.Noticing these limitations,some multi-view clustering methods[Xu,Wang and Lai(2016);Xu,Han,Nie et al.(2017)]have been proposed to learn the corresponding distribution of different views.

Inspired by the above work,we propose a robust re-weighted multi-view feature selection method(RRMVFS)without concatenation.For each view,we make the predictive values close to the real labels,and construct the penalty term by using the least-absolute criterion,which can not only induce robustness but also learn the corresponding view weights adaptively without any presetting parameter.Based on the proposed penalty,the scheme is established by addingG1-norm andl2,1-norm regularization terms for the structured sparsity.In the procedure of optimization,the proposed model can be decomposed into several small scale subproblems,and an iterative algorithm based on Iterative Re-weighted Least Squares(IRLS)[Daubechies,Devore,Fornasier et al.(2008)]is proposed to solve the new model.Furthermore,the theoretical analysis of convergence is also presented.

In a nutshell,the proposed multi-view feature selection method has the following advantages:

·It can fully consider the complementary property of multiple views as well as the specificity of each view,since it assigns all views of each sample to the same class while separately imposes penalty for each view.

·It can reduce the influence of outliers effectively because the least-absolute residuals of each view are combined as penalty.

·It can learn the view weights adaptively by a re-weighted way,where the weights are updated according to the current weights and bias matrix without any presetting parameter.

·It can be efficiently solved due to the following two reasons.One is that the objective function can be decomposed into several small scale optimization subproblems,and the other one is that IRLS can solve the least-absolute residual problem within finite iterations.

·Extensive comparison experiments with several state-of-the-art feature selection methods show the effectiveness of the proposed method.

The paper is organized as follows.In Section 2,we present our feature selection model and algorithm in detail,and the convergence of the proposed algorithm is analysed.After presenting the extensive experiments in Section 3,we draw the conclusions in Section 4.Now,we give the notation in this paper.GivenNsamples which haveVviews belonging toPclasses,the data matrix of thevth view is denoted asis thevth view of thenth sample,anddvis the feature number

of thevth view,v=1,···,V.The data matrix of all views can be represented by where

2 Robust re-weighted multi-view feature selection method

2.1 Model formulation

In order to select the relevant views and feature subset from the original ones,we first use label information of the multi-view data to build the penalty term through the loss minimization principle.We calculate the penalty term by least-absolute criterion which can induce robustness.Instead of concatenating all views as long vectors,the penalty term is established as the sum of the residuals calculated on the latent subspace of each view:

Formulation(2)assigns all views of each sample to the same class,and imposes the penalty separately on each view.It simultaneously considers the complementary property of different views and the specificity of each view.

whereb(v)∈RPis a bias vector of thevth view,and1N ∈RNis the vector of all ones.The residuals are not squared and thus outliers have less effect compared with the squared residuals.Since different views have different effects for a specific class,we useG1-norm regularizer to enforce the sparsity between views.Meanwhile,we usel2,1-norm regularizer which has the ability of imposing the transformation matrix sparse between rows to select the representative features.The formulation of the proposed multi-view feature selection method can be described as follows:

2.2 Optimization algorithm

Next we give an iterative optimization algorithm to solve the problem(2).Firstly,we transform the objective function of(2)as:

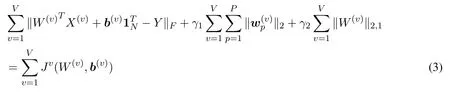
SinceJv(W(v),b(v))is only related to thevth view and nonnegative,the problem(2)can be decomposed into solvingV-subproblems:

Note that the problem(4)cannot be easily solved by the sophisticated optimization algorithms since its objective function is nonsmooth.We utilize IRLS method[Daubechies,Devore,Fornasier et al.(2008)]to solve it,and change it as follows:

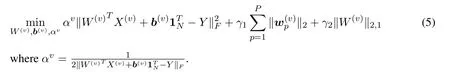
1.Fixαv,updateW(v),b(v).For problem(5),we can solve the following problem iteratively with the fixedαv:

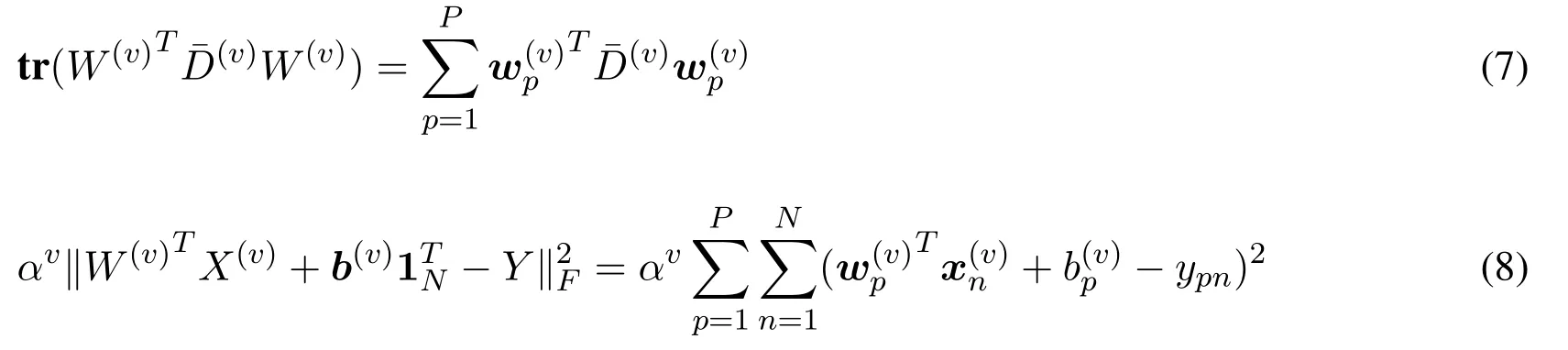
Taking the derivative of the(10)with the respect toandand setting them to zeros,we can obtain

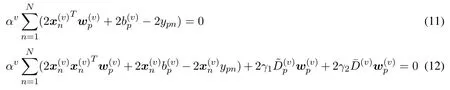
So from(11),we have

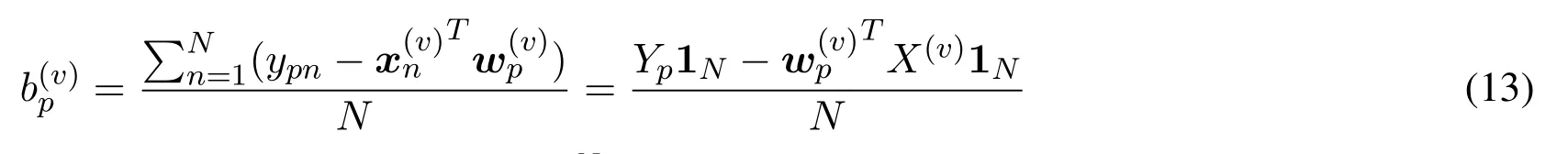
whereYp=(yp1,···,ypN)∈RN.Substituting(13)into(12),we have

2.FixW(v),b(v),updateαv.The non-negative weightαvfor each view can be updated as

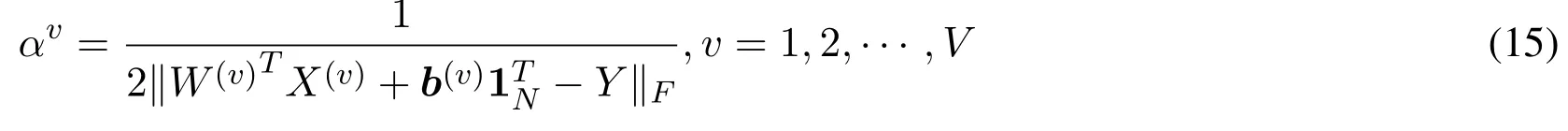
The proposed multi-view feature selection algorithm(RRMVFS)is summarized in Algorithm 1.

2.3 Convergence analysis

Theorem 1.The values of the objective function of(2)monotonically decrease in each iteration in Algorithm 1,and the algorithm converges.

Proof:From Eq.(3),in order to proveJ(Wt+1,Bt+1)≤J(Wt ,Bt),we only need to prove thatJv(W(v),b(v))monotonically decreases in each iteration.

Algorithm 1:RobustRe-weighted Multi-view FeatureSelection(RRMVFS)Input:data matrix of each view X(v),v=1,2,···,V,label matrix Y=[y1 ,y2 ,···,yN ].Output:transformation matrix W(v),v=1,2,···,V.Initialization 1.Set t=0,threshold∈=10-5,the largest iterative number T=20;Set(W(v))0 ∈ Rdv×P(v=1,···,V)all elements 1,and(b(v)p )0 can be calculated by(b(v)p)0=Yp 1N -(w(v)(1≤p≤P,1≤v≤V)as well as(αv)0 = 1 p)0 TX(v)1N(1≤v≤V)while not converged do 2.Compute the diagonal matrices(¯D(v))t (1≤v≤V)with the ith diagonal element 1 N 2‖(W(v))0TX(v)+(b(v))01TN -Y ‖F 2‖(W(v)i:)t-1‖2;Compute the diagonal matrices(˜D(v)p )t =Idv (1≤v≤V)with Idv being an identity matrix.3.For each w(v)p and b(v)p (1≤ p≤ P,1≤v≤V),compute(w(v)p)t+1=((αv)tX(v)HX(v)T+γ1(˜D(v)p)t+γ2(¯D(v))t)-1(αv)tX(v)HYTp,and(b(v)p)t+1=Yp 1N -(w(v)1 2‖(w(v)p)t-1‖2 p)t+1 TX(v)1N 4.Calculate(αv)t +1 = 1(1≤v≤V);5.Check the convergence condition J(Wt ,Bt )-J(Wt +1 ,Bt +1 ) ＜ ∈(J(·,·)is the objective function of(2))or t＞T;6.t=t+1;End While N 2‖(W(v))t+1TX(v)+(b(v))t+11TN -Y ‖F

By Step3 in Algorithm 1,we have

From(17)-(20),we obtain

So,wegetJ(Wt+1,Bt+1)≤J(Wt ,Bt),thatis,Algorithm1decreasestheobjectivevalues in each iteration.SinceJ(W,B)≥0,Algorithm 1 converges.

3 Experiments

In this section,we evaluate the effectiveness of the proposed method by comparing it with several related feature selection methods.

3.1 Experimental setup

We compare the performance of our method RRMVFS with several related methods:Single,CAT,RFS[Nie,Huang,Cai et al.(2011)],SSMVFS[Wang,Nie and Huang(2013)],SMML[Wang,Nie,Huang et al.(2013)],DSML-FS[Gui,Rao,Sun et al.(2014)],and WMCFS[Xu,Wang and Lai(2016)].Single refers to using single-view features to find best performance for classification.CAT refers to using concatenated vectors for classification without feature selection.RFS is an efficient robust feature selection method,but not designed for multi-view feature selection.The other feature selection methods are designed for multi-view feature selection.The parametersγ1andγ2in feature selection methods are tuned from the set{10i|i=-5,-4,···,5}.The exponential parameterρin WMCFS method is set to be 5 according to Xu et al.[Xu,Wang and Lai(2016)].

The public available data sets,including images data set NUS-WIDE-OBJECT(NUS),handwritten numerals data set mfeat,and Internet pages data set Ads are employed in the experiments.For NUS data set,we choose all 12 animal classes including 8182 images.For Ads,there exist some incomplete data.We first discard the incomplete data and then randomly choose some non-AD samples so that the number of non-AD data is the same as that of AD data.The total number of the samples employed in Ads is 918.For mfeat data set,all of data are employed.In each data set,the samples are randomly and averagely divided into two parts.One part is used for training and the other part is used for testing.In the training set,we randomly choose 6(9,or 12)samples from each class to learn transformation matrix of these compared methods.In the test set,we employ 20%of data for validation,and the parameters that achieve the best performance on the validation set are employed for testing.We arrange features in descending order based on the values of‖Wi:‖2,i=1,2,···,d,and select a certain number of top-ranked features.The numbers of selected features are{10%,···,90%}of the total amount of features,respectively.Then the selected features are taken as the inputs of the subsequent 1-nearest neighbour(1NN)classifier.Weconducttwokindsofexperiments.First,weconductexperimentsonallviews to evaluate these methods.Then,we conduct experiments on the subsets formed by two views and four views to make the evaluation of views.For all experiments,ten independent and random choices of training samples are employed,and the averaged accuracies(AC)and F1 scores(macroF1)are reported.

3.2 Evaluation of feature selection

Figs.1,2,and 3 show the performance of the compared methods w.r.t.the different percentages of selected features on NUS,mfeat and Ads data sets,respectively.From thesefigures,we can see that,the performance of these methods under AC are consistent with the one under macroF1 scores.CAT has the better performance than Single in all cases,which means that it is essential to combine different views to select features.The feature selection methods,including ours,achieve the comparable or even better performance than CAT.Specifically,from Fig.1,we can see that three feature selection methods including RFS,SSMVFS,and DSML-FS show the comparable performance on NUS data set.SSMVFS and DSML-FS are the feature selection methods designed for multi-view learning,while RFS is a robust feature selection method that is not specially designed for multi-view learning.This means that it is necessary to build a robust method since data may be corrupted with noise.Along with the number of selected features increasing,the ACs and macroF1 scores of the multi-view feature selection methods WMCFS,SMML,and the proposed RRMVFS are greatly improved.Moreover,RRMVFS achieves the best results in most cases.This phenomenon might be attributed to the robust penalty which may help RRMVFS select more representative features.

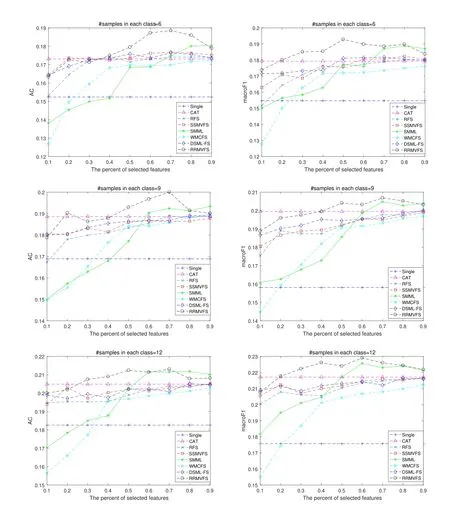
Figure1:ACs and macroF1 scores of compared methods vs.percents of selected features on NUS data set

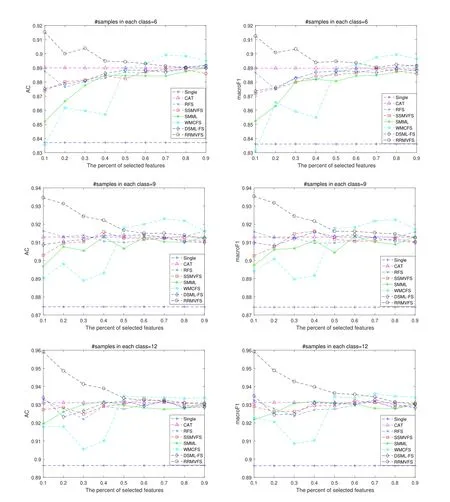
Figure2:ACs and macroF1 scores of compared methods vs.percents of selected features on mfeat data set

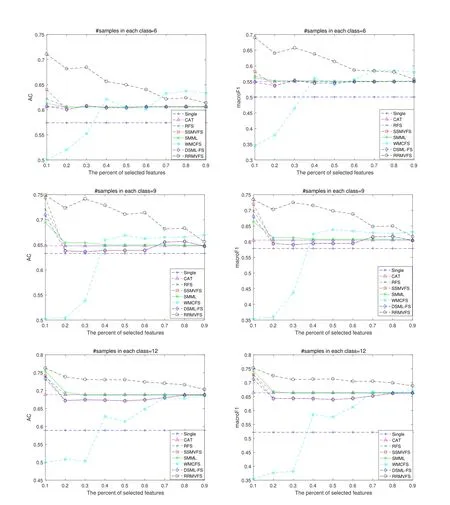
Figure3:ACs and macroF1 scores of compared methods vs.percents of selected features on Ads data set

From Fig.2,we can see that RFS,SSMVFS,and DSML-FS show the comparable performance on mfeat data set.Along with the number of selected features increasing,the ACs and macroF1 scores of SMML and WMCFS are increased except at a few percentages,especially for WMCFS.The proposed RRMVFS can achieve the best performance when only a small number of features(the percent of selected features is 10)are selected.

From Fig.3,we can see that four feature selection methods including RFS,SSMVFS,SMML,and DSML-FS obtain comparable performance on Ads data set.They achieve their best performance at 10%,and when the percentages of selected features change from 20%to 90%,their ACs and macroF1 scores are substantially unchanged and comparable to those of CAT.Just like the performance on the other two data sets,the proposed RRMVFS still achieves the best performance on Ads data set.

3.3 Evaluation of views

In order to evaluate the effect of views,we test ACs and macroF1 scores of the compared methods in terms of views on NUS,mfeat,and Ads data sets,respectively.The experiments are conducted on the subsets that contains 12 samples of each class.For each data sets,we conduct two kinds of experiments.Firstly,we randomly choose two views for experiments.Secondly,we randomly choose two views from the remaining views,and combine them with the previous two views to form the subsets for experiments.

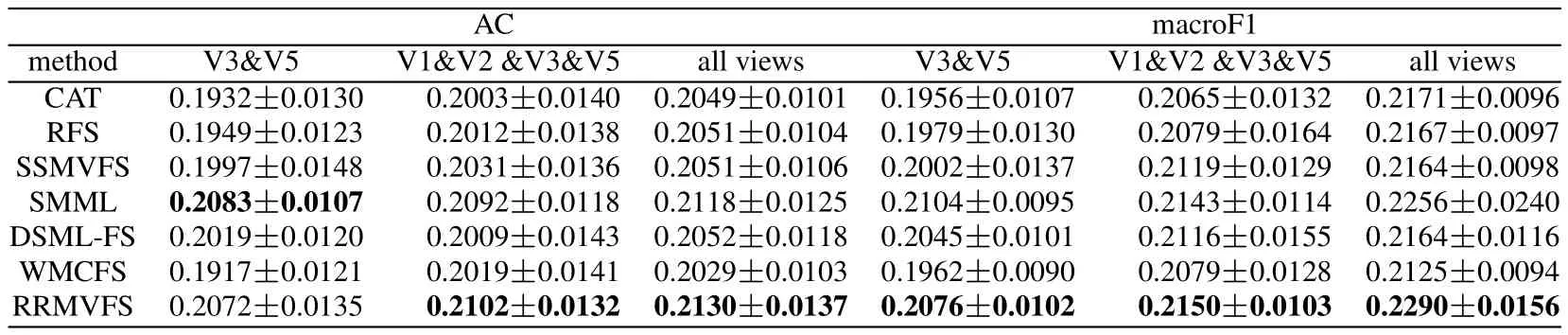
Table1:ACs and macroF1 scores with standard deviation of the compared methods in terms of views on NUS data set

The experimental results on these three data sets are shown in Tabs.1-3,respectively.It can be seen that with the increase of views,generally speaking,the performance of all compared methods gets better.On the subsets which consist of two views,our method RRMVFS does not show the best performance,but on the subsets formed by four views and the whole sets,our method is superior to others significantly.This phenomenon might be attributed to the learning of view weights which may help RRMVFS select more relevant views.

Table2:ACs and macroF1 scores with standard deviation of the compared methods in terms of views on mfeat data set

Table3:ACs and macroF1 scores with standard deviation of the compared methods in terms of views on Ads data set

4 Conclusion

In this paper,we have proposed a robust re-weighted multi-view feature selection method by assigning all views of each sample to the same class while imposing penalty based on latent subspaces of each view through least-absolute criterion,which can take both the complementary property of different views and the specificity of each view into consideration and induce the robustness.The proposed model can be efficiently solved by decomposing it into several small scale optimization subproblems,and the convergence of the proposed iterative algorithm is presented.The comparison experiments with several state-of-the-art feature selection methods verify the effectiveness of the proposed method.Many real-world applications,such as text categorization,are multi-label problems.The future work is to develop the proposed method for multi-label multi-view feature selection.

Acknowledgement:The work was supported by the National Natural Science Foundation of China(Grant Nos.61872368,U1536121).