Heterogeneous Memristive Models Design and Its Application in Information Security

Shaojiang Ζhong

Abstract: Based on the three-dimensional classic Chua circuit,a nonlinear circuit containing two flux-control memristors is designed.Due to the difference in the design of the characteristic equation of the two magnetron memristors,their position form a symmetrical structure with respect to the capacitor.The existence of chaotic properties is proved by analyzing the stability of the system,including Lyapunov exponent,equilibrium point,eigenvalue,Poincare map,power spectrum,bifurcation diagram et al.Theoretical analysis and numerical calculation show that this heterogeneous memristive model is a hyperchaotic five-dimensional nonlinear dynamical system and has a strong chaotic behavior.Then,the memristive system is applied to digital image and speech signal processing.The analysis of the key space,sensitivity of key parameters,and statistical character of encrypted scheme imply that this model can applied widely in multimedia information security.

Keywords: Chua circuit,heterogeneous memristor,flux-control memristor,hyperchaos system,data image encryption.

1 Introduction

There are four basic variables in circuit theory:currenti,voltagev,chargeq,and magnetic fluxφ,so there are=6possible combinations of relation between any two variables.Five relationships have been discovered before which arev-i,v-q,v-φ,i-q,i-φ,but what is the relationship between fluxφand chargeq? Professor Leon O.Chua at the University of California,Berkeley,predicted their existence in 1971 based on the completeness and symmetry of the circuit statistics [Chua (1971)].The fourth basic circuit component named memristor (short for memory and resistor),forms a complete circuit system with the original capacitorsC,resistorRand inductorL(see Fig.1).In 2008,Strukov and his colleagues of Hewlett-Packard (HP) Labs fabricated a nanometer-sized TiO2 memristor,the features of the circuit are consistent with the characteristics of the resistive device predicted by Leon O.Chua [Strukov,Snider,Stewart et al.(2008)].In 2010,HP Labs once again announced that the memristor apparatus has Boolean logic operation function,this discovery shocked the computer field [Vaidyanathan,Pham and Volos (2017);Duan,Zhang and Hu et al.(2014);Qu,Zhu and Wang et al.(2018)].

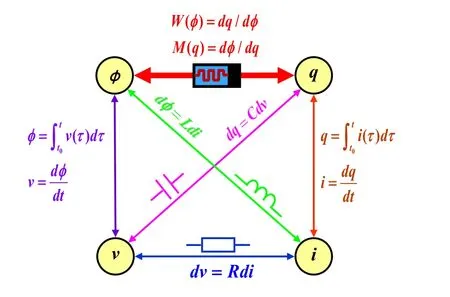
Figure1:Correlation of the memristor with four basic circuit variables

Hence,the research of memristor has been widely developed and applied in various fields[Peishin and Di Ventra (2011);Yakopcic,Hasan and Taha (2017);Wang,Wang and Zhou (2016)].Researchers in Germany have produced learning-capable nanomemristor devices,each of them is only 600 times the diameter of a human hair [Thomas (2013)].As a key part of designing an artificial brain,the memristor mimics human neural function.Biolek established a SPICE macro model of TiO2 memristor to study the physical and circuit characteristics of memristor under the condition of nonlinear drift[Biolek,Biolek and Biolkova (2009)].IBM Zurich research center announced the creation of the world’s first 500 artificial nanoscale random phase-change neuron arrays[Tuma,Pantazi,Le et al.(2016)] to simulate the way the human brain works.Bao et al.[Bao,Liu and Xu (2010)] researched the characters of smooth flux-controlled memristor and set up a new chaotic circuit.Zeng et al constructed and simulated synchronization of memristor-based on Chua’s circuits [Wen,Zeng,Huang et al.(2013)].Professor Hu and Duan et al proposed several design operations of Cellular Neural Networks (CNN) image processing based on the memristor [Hu,Duan,Chen et al.(2017);Hu,Feng,Liu et al.(2015)],which demonstrated the nonlinear behavior through simulation and comparison,and designed the reverse tandem memristor synaptic circuit.

Nonvolatile random memory is expected to be realized by the appearance of nanometer memristor.The integration,power consumption and reading and writing speed of the random memory based on memristor are superior to the traditional random memory[Bilotta,Chiaravalloti and Pantano (2014);Sah,Kim and Chua (2014);Wang,Ma,Xu et al.(2017)].In addition,memristor is the best way for hardware to realize synapse of artificial neural network.Since memristor is also composed of nonlinear models,it is easy to associate with chaotic systems [Wu,Wang,Jin et al.(2017);Sheridan,Cai,Du et al.(2017);Uçar and Yavşan (2016)].In fact,many existing memristic models are generated by nonlinear equations or circuits [Pham,Jafari,Vaidyanathan et al.(2016)].The chaotic system is vulnerable and sensitive to external environment,so it can be applied in the information encryption and secret communication.At the same time,due to the diversity of model parameters,large key space can be generated to increase the difficulty of cracking.

In this paper,a 5-dimentional flux-controlled memristors based on classical Chua’s circuit are put forward.Numerical simulation shows that system variables have obvious chaos trajectories and complex nonlinear dynamical behaviors,also including memristic characters.This model can be successfully applied to the scrambling and encryption of image and speech information,so the memristive model will provides a reference for the further study of the memory chaotic system and information processing.

2 Heterogeneous memristor system construction

The memristor can remember the number of charges flowing through it,and at any given moment the resistance is a function of time,and it changes with the current passing through.

2.1 Memristor properties

Memristor is a kind of nonlinear resistor with memory function.The resistance value can be changed by controlling the change of current.If the high resistance value is defined as“1” and the low resistance value is defined as “0”,the resistance can realize the function of data storage.It is actually a non-linear resistor with memory.

Memristor has three essential characteristics summarized as [Adhikari,Sah,Kim et al(2013)]:

(1) When a periodic excitation voltagev(t)(or currenti(t)) signal is connected to the outside,thev(t) -i(t)characteristic curve of the memristor is a zero crossing point.The shape of pinched hysteresis loop is presented as italic digital “8”,and the whole curve has odd symmetry and periodicity;

(2) When the frequencyωof the applied excitation signal increases to a larger value,thev(t) -i(t)plane area of the pinched hysteresis loop will decrease with the increase of the frequency of the input excitation signal;

(3) When the frequencyωof the applied electric signal tends to infinity,the pinched hysteresis loop will shrink into a straight line,and the nonlinearity of the memristor will disappear,and the resistance will be a constant value.

These are the typical features of the ideal memristor and the criterion of its judgment.

2.2 Dual flux-control memristor model

From Fig.1,memristor is a new two-terminal circuit element in which there is a functional relationship between chargeqand magnetic fluxφ.Assumingvandistand for voltage and current respectively,according to the basic principles of the circuit,the memristanceM(q)and memductanceW(φ)can be expressed as following:

andM(q)(Ohm) andW(φ)(Siemens) have physical definitions as

In this paper,we construct 2 different memductancesW1(φ1)andW1(φ1),whose expressions are given by

wherea,b,c,d,eare real constants.

To reveal that the modelsW1andW2in Eq.(3) possess three essential characteristics of memristor described in Section 2.1,selecting a periodic excitation sinusoidal voltagesv=Vmsin (ωt) =Vmsin(2πft),whereVmis voltage amplitude,ωandfare angular and frequency,respectively.

Assuminga=1.923,b=1.923,c=-1.9230.9,d=1.9615,e=0.09615in Eq.(3),by replacing Eq.(3) with Eq.(1),Fig.2 shows thev-icurves ofW1andW2memristors withω=(1,0.5,0.35)Hz angular frequency,we can show they have shapes like italic digital ‘8’,they possess obvious pinched hysteresis loop features.

Figure2:Thev - icurves of two different memristors with W1 and W2

2.3 Dual memristors structure based on classic Chua's circuit

The classic Chua’s chaotic circuit is consisted by two capacitorsC1andC2,an inductorLand a Chua’s nonlinear resistance diode [Muthuswamy and Chua (2010)].

Fig.3 draw a novel dual memristor-based Chua’s circuit,which is synthesized by 1 inductorL,2 linear resistorsRandr,2 capacitorsC1andC2,2 different memristorsW1andW2.

According to Kirchhoff Current Laws (KCL) and Kirchhoff Voltage Laws (KVL),we can obtain the following equations from Fig.3.

Figure3:Heterogeneous dual flux-control memristive circuit

Combining two different structure magnetic-controlled memristorsM1andM2,Eq.(4)is changed as:

Substitute formula (3) into formula (4),and we can obtain

3 Chaos nonlinear performs of the dual heterogeneous memristors

In this section,we will use numerical simulation to display the state trajectory of the system(6) and analyze the nonlinear characteristics of the two novels designed memristors.

3.1 Dual memristors numerical simulation

Let the coefficients of Eq.(6) areC1= 0 .18,C2= 1 .923,R= 0 .52,L= 0 .05,r=0.0125,and parametersa=1.923,b=1.923,c=-1.9230.9,d=1.9615,e=0.09615,the trajectory diagrams of system (6) are drawn in Fig.4.

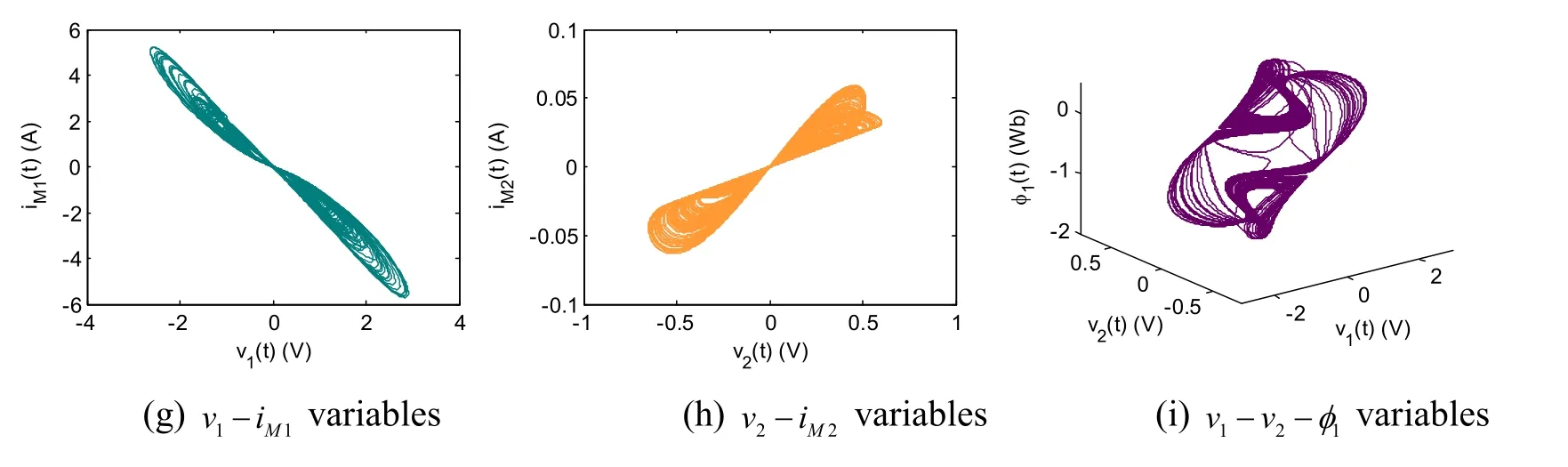
Figure4:Variable phase portraits and trajectories of Eq.(6)

Figs.4(a)-4(f) show there are obvious dual-scroll chaotic attractors,and Fig.4(i) displays 3-D complex trajectory,Figs.4(g) and 4(h) showv(t) -i(t)trajectories ofW1andW2flux-controlled memristors ,they present a pinched hysteresis loop and similar to Fig.2.

3.2 Main chaotic features with dual memristors

In order to fully verify the chaotic characteristics of system (6) with dual memristors,we verify it from the following aspects:

A) Lyapunov exponent

The Lyapunov exponent can characterize the motion of the system,it is the magnitude of positive and negative values along a certain direction and represents the average divergence or convergence of adjacent orbits in the attractor in a long time.For chaotic systems,Lyapunov exponent can describe quantitatively the degree of separation of orbits of dynamic systems in phase space.The Jacobian matrix of system (6) is

Adopting Jacobian matrix method,Lyapunov exponents of system (6) are calculated:LE1=0.7896,LE2=0.4131,LE3=-0.3092,LE4=-0.5225,LE5=-4.5787.There are two positive Lyapunov exponents and the sum of the Lyapunov exponents is negative,indicating hyperchaotic behaviour.

The Lyapunov dimension is:

DLis a fractal dimension.

Fig.5(a) displays the Lyapunov exponents change of the system (6) within parameterb∈[0,3],Fig.5(b) displays the Lyapunov exponents of the system (6) with timetvaries,and whent＞ 10ms,LE1＞0andLE2＞0,which show the double memristor system is also a hyperchaotic system.

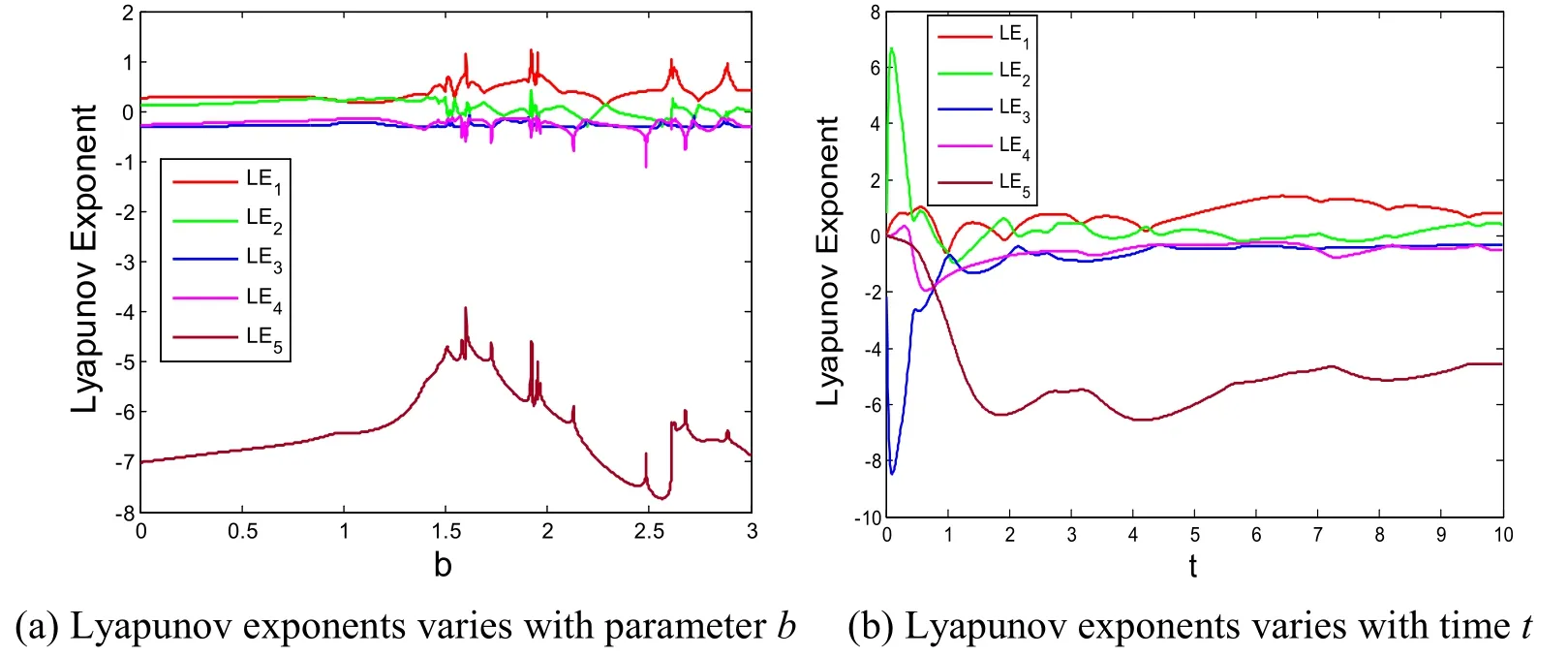
Figure5:Lyapunov exponents of the system (6)

B) Equilibrium point and eigenvalue

For system (6),let each of these terms is equal to 0,namely

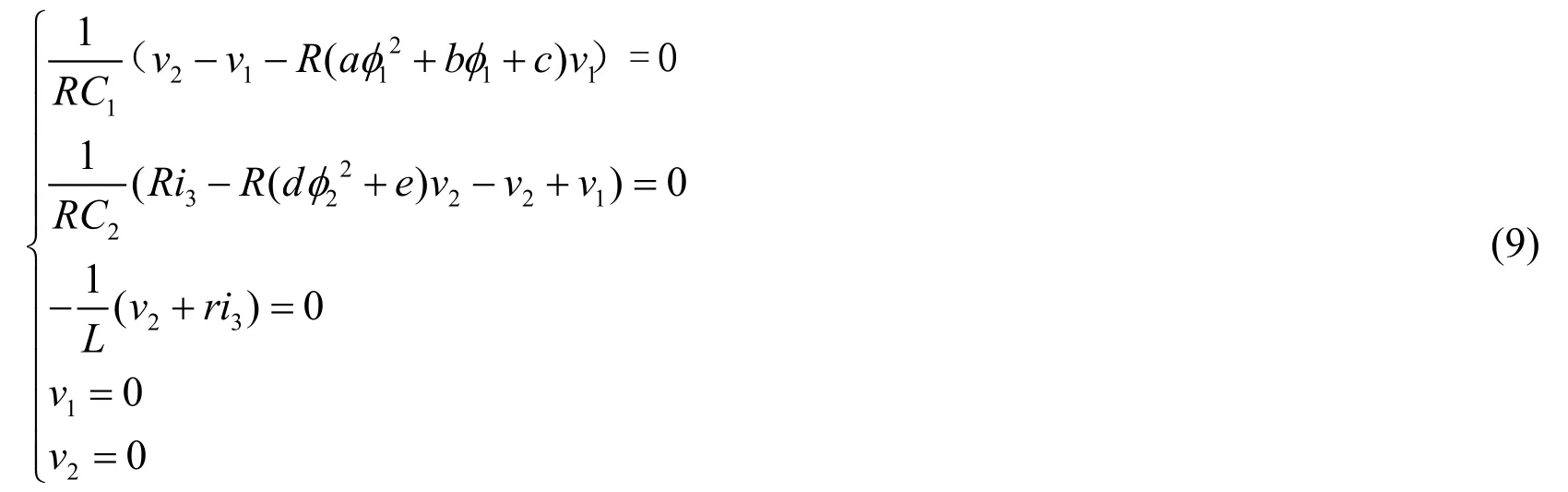
There is only one equilibriumS*=(0,0,0,0,0),the Jacobia matrix withS*is

Eigenvalues are calculatedλ1,2=0,λ3,4= -1 .1832 ± 1 .0496 ＜ 0,λ5= 1 .0659 ＞ 0,this indicates that the equilibrium pointS*is an unstable saddle point.

C) Poincare map

Poincare cross section is used to analyse the motion of multi-variable autonomous system.If the transient transition process of the initial stage is not considered,the steady-state image of the Poincare section is only considered.When there is only one fixed point and a few discrete points on the Poincare section,the motion can be determined as periodic.When the Poincare section is a closed curve,it can be determined that the motion is quasi-periodic,and when the Poincare section is a dense point with a hierarchical structure,it can be determined that the motion is in a chaotic state.

Fig.6 showsv2-i3profile (wherev1=0.5) andv1-v2profile (wherei3=3)respectively,listing signs of complex folding.

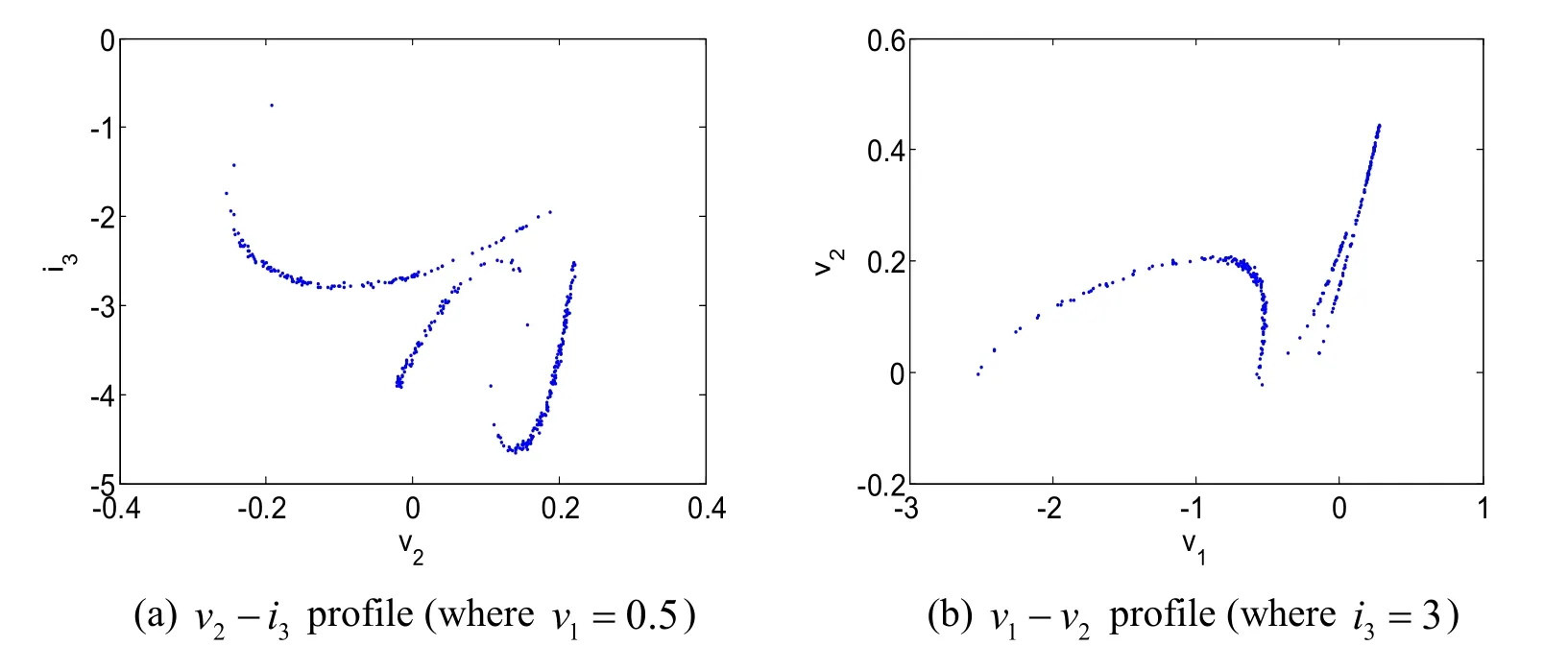
Figure6:Poincare map of the system (6)

D) Power spectrum

Power spectrum analysis is an important means to study vibration and chaos.According to Fourier series expansion,the frequency of chaotic aperiodic dynamics is continuous spectrum.Fig.7 shows the system (5) is a continuous spectrum.

Figure7:The continuous power spectrum with variable v1

E) Bifurcation diagram

When the system parameter changes,the projection of Poincare mapping on a coordinate axis can constitute the bifurcation diagram.The countless points drawn in a chaotic graph indicate that there are numberless periodic signal points that never fall into the same position when chaos occurs.In the bifurcation diagram (Fig.8),the characteristics of system performance change with system parameters can be clearly described.

4 Data signal security with heterogeneous memristors

Chaos is a random behavior generated by deterministic equation,which is extremely sensitive to initial conditions and parameters,as well as long-term unpredictability.It can be used for confusion and synchronization control in secure communication field.In this section,we apply the constructed dual memristors to the encryption of digital image and voice signal.

4.1 Digital image secure scheme

Now let us describe the secure image communication scheme,for the case the image to be sent is a 24-bit RGB image.For other format images,the scheme is still effective after slightly adjustment.First,we define the key set of the scheme as follows:

where

●k1～k5are the initial conditions ofv1(0),v2(0),i3(0),φ1(0),φ1(0)with Eq.(6);

●k6～k10are the parametersC1,C2,L,R,rof heterogeneous memristors of Eq.(5);

●k11～k15are the parameters of two memristors (a,b,c,d,e)which are selected with Eq.(3);

In order to achieve the encryption of the original image information,the chaotic sequence in system (6) is used to mix up the RGB color image sufficiently,as far as possible to achieve a Gaussian white noise effect.

AM×Npixels color image is selected in the experiment,the encryption result is show as Fig.9.Fig.9(a) is the secret color image,it has 256×213 pixels.Fig.9(b) is encryption image,it has completely obscured the original image and is impossible to guess.Fig.9(c)is correct decryption image without any key error.

4.2 Security analysis

In the following subsections,key space and sensitivity analysis are given.The results show that our scheme has satisfactory security.

●Key space.The keys used in the scheme are double precision numbers.There are 15 keys altogether defined as Eq.(11).The sensitivity of the keys is 10-16.For the reason that guarantees to generate chaotic orbits,and the effective bits ofKs,consequently the size of the key space is 10(16×15)=10240＞2797.If we adopt brutally attack in search of the exact key value,time complexity is tremendous!

●Key sensitivity.Tab.1 shows that encrypted images are very sensitive to perturbations of the keys (k2,k9,k12) = (v2(0),R,b).That is to say,when we first encrypt the original image withki,the cipertext is calledCi,then re-encrypt the plaintext withki+Δ,commonly Δ=1e-14,1e-15,1e-16,the new cipertext is calledCj,other 12 keys are unchanged.The percent of pixel error betweenCiandCjis over 99%,the results are shown in Figs.9(d)～9(f).In fact,our computer simulation shows that encrypted images are also very sensitive to perturbations of the other 12 keys.

In other words,if we encrypt withkikey,but decrypt withki+Δkey,we will get the similar non-decryption effects.

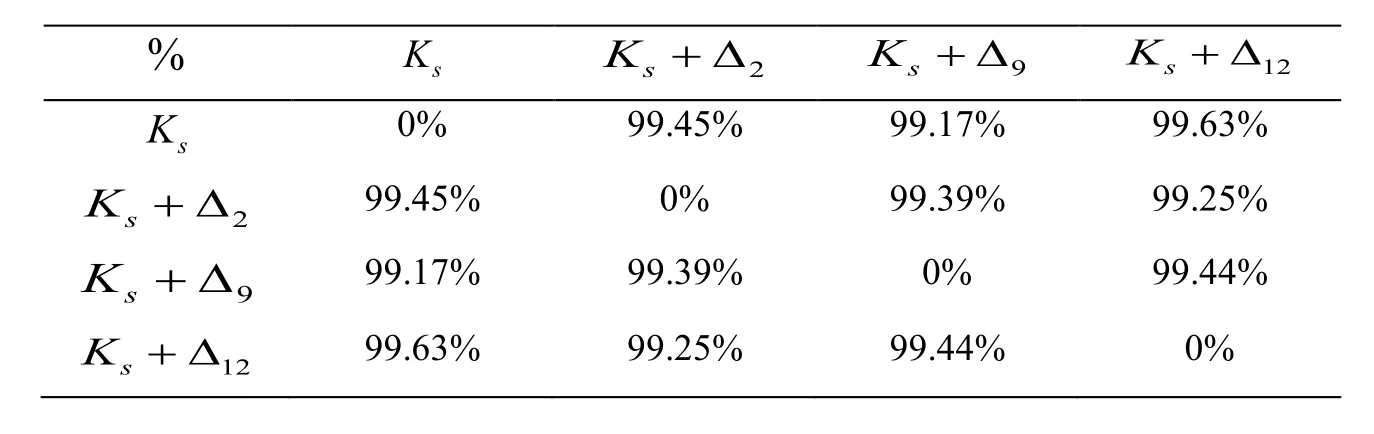
Table1:Sensitivity analysis of cipher image between Ciand Cj

Figure9:Data image encryption result and the key sensitivity analysis

●Statistical analysis.Let us compare the histograms between the plaintext (original imageP) and the encrypted imageQ.Select the original imagePshown in Fig.9(a),the histograms of the intensity level of RGB color planes are shown in the first row in Fig.10.The graphs given in the second row in Fig.10 are the histograms of the intensity level of the encrypted imageQ,that is shown in Fig.9(b).It can be seen that the histograms of the cipher images are more flat and are significantly different from those of the plaintext image.This illustrates the encryption image has quite chaotic.

●Speech signal security.We can also encrypt and protect the speech signal by using a scheme similar to that of image encryption.Fig.11 shows the all processes of encryption and decryption.

● Actually,origin speech signal in Fig.11(a) is single track,that is to say we can use a part of system (6) serial,the attacker doesn't know the number of equations we choose,and this adds more obstacles to decryption.

●Fractional order test.The fractional order equation is also used to process the system (5),the test results show that this design scheme is also suitable for fractional memristor systems.Different fractional value selection will increase the space of the key and the complexity of the algorithm.

●Others.In order to verify the chaotic behavior of the dual memristors,we can consider designing analog or digital circuits,that's the path to real physics,they are the extensive work in the future.

Figure10:Histogram comparison with origin image and cipher image

Figure11:Speech signal secure communication with similar image scheme

5 Conclusion

In this paper,a novel memristive circuit is proposed with two flux-controlled smooth memristors.Furthermore,analyzing the Lyapunov exponent spectrum,equilibrium point and phase portraits,and indicate this system has also the hyperchaotic nonlinear characteristics.The scheme has 15 keys and the key space is larger than 2797,which should be large enough for the requirements of secure communications.The sensitivity of the keys and the uniformity of the histograms of encrypted images imply that the new secure communication scheme is a promising candidate for images transmission.This scheme may be suitable for many format image encryptions and is feasible to color image secure communication and can be applied to speech and other multimedia signal encryption.