Enabling Comparable Search Over Encrypted Data for IoT with Privacy-Preserving

LeiXu,ChungenXu,,ΖhongyiLiu,YunlingWangandJianfengWang

Abstract: With the rapid development of cloud computing and Internet of Things (IoT)technology,massive data raises and shuttles on the network every day.To ensure the confidentiality and utilization of these data,industries and companies users encrypt their data and store them in an outsourced party.However,simple adoption of encryption scheme makes the original lose its flexibility and utilization.To address these problems,the searchable encryption scheme is proposed.Different from traditional encrypted data search scheme,this paper focuses on providing a solution to search the data from one or more IoT device by comparing their underlying numerical values.We present a multiclient comparable search scheme over encrypted numerical data which supports range queries.This scheme is mainly designed for keeping the confidentiality and searchability of numeric data,it enables authorized clients to fetch the data from different data owners by a generated token.Furthermore,to rich the scheme’s functionality,we exploit the idea of secret sharing to realize cross-domain search which improves the data’s utilization.The proposed scheme has also been proven to be secure through a series of security games.Moreover,we conduct experiments to demonstrate that our scheme is more practical than the existed similar schemes and achieves a balance between functionality and efficiency.

Keywords: Internet of things,encrypted data search,multi-client,privacy-preserving.

1 Introduction

With the increasing development of cloud computing [Popović and Hocenski (2010);Buyya,Yeo,Venugopal et al.(2009)] and Internet of Things application [Lin,Yu,Zhang et al.(2017);Farooq,Waseem,Khairi et al.(2015)],data security is getting more and more attention all over the world.As we know,in an IoT scenario,data is collected from different devices and aggregated into the network and stored on the cloud.To save local cost and improve computing power,industries begin to outsource their data to third parties for storage and management.Along with this trend,various of cryptography protocols and schemes [Song,Li,Mei et al.(2017);Liu,Peng and Wang (2018)] are proposed to keep the privacy of the data,searchable encryption [Chor,Goldreich,Kushilevitz et al.(1995);Boneh,Di Crescenzo,Ostrovsky et al.(2004)] is one of those which focuses on maintaining searchability of the encrypted data on the cloud.It enables an authorized client to search the encrypted data by a token of the expected keyword without leaking anything of the keyword.After a long period of research,searchable encryption has evolved many variants based on the demands of different scenarios and functions [Wang,Cao,Li et al.(2010);Baek,Safavi-Naini and Susilo (2008);Golle,Staddon and Waters (2004)].For example,public key encryption scheme with keyword search provides a solution to the problem of data searching in email system,encrypted search scheme with conjunctive keywords allows the users to search a file which contains both keyword “urgent” and“important”.All of them can provide convenient services for people.

However,with the highly developed of the information technology,existing searchable encryption constructions cannot satisfy people’s requirements any more.Traditional searchable encryption schemes always provide an exactly search method,which can only lock to the keyword you want [Li,Yu,Cao et al.(2011);Li,Li,Chen et al.(2012)].While for a special scenario on encrypted numeric data that a doctor wants to find the records of the patients,whose body temperature is higher than 36oC,to help him analyze the cause,he needs to find all the possible values and computes the corresponding token of them,then sends the query application to the service provider to get the search results.This approach is undoubtedly too complicated to be adopted for massive data search.To address this problem,a protocol called order-preserving encryption (OPE) scheme[Agrawal,Kiernan,Srikant et al.(2004);Boldyreva,Chenette and O’Neill (2011)] was proposed to solve the problem of these numeric data search.As its name suggests,the ciphertext produced by order-preserving encryption preserves the order of the underlying value.However,it was soon discovered that this ORE cryptography system had a fatal flaw [Naveed,Kamara and Wright (2015);Li,Zhang,Yang et al.(2015)],that is,an attacker,just like the service provider can recover the plaintext database by comparing and ordering the total dataset without authorization.Fortunately,some improvements,such as comparable encryption [Furukawa (2014)] and order-revealing encryption (ORE),were quickly put forward to replace the ORE scheme to alleviate the above dilemma,the mainly difference is that these two schemes both need an addition token to performs the comparing operation.By this,only the authorized client with the token can performs comparable search.

Motivations.Although comparable encryption scheme provides us the capability to make range queries by comparable search,there are also several shortcomings which are not addressed well.The first thing is that traditional basic comparable encryption or order revealing encryption schemes are always built under the model of single writer/single reader,i.e.,only the data owner herself can search or perform comparing search their data.This will limit the utilization of the data and not meet the concept of data sharing or create opportunities for conditional sharing.Nowadays,some work has been done to improve the practice of the scheme by allowing more users to enjoy data sharing and searching service,one general approach is to add the access control policy which cannot address the problem of data security essentially.Once an attacker goes past all the access control policy and gains the right of visiting the database,he can fetch all the data which he is interested in.So the best way to overcome this trouble is to adopt cryptographic protocols to eliminate these threats fundamentally.However,the use of cryptographic technique will inevitably introduce addition computation and communication overhead.Finding a practical,secure and efficient comparable searchable encryption scheme is an interesting and urgent.Fortunately,these problems have attracted the attention of some researchers,and many classical schemes were proposed to solve them.The main idea is to introduce a private key generator (PKG) to manage the keys of the users that will raise another problem,the right of PKG is so strong that all the users’ private keys are in her control.There will be irreparable damage if she is attacked or leaks the private key of the user.In this regard,how to design a private key generation method is also crucial.

Contributions.To address the problems mentioned above and provide a practical solution for encrypted data search,we propose a new comparable searchable encryption scheme in this paper with some superior properties.First,we deploy the idea of comparable encryption to design a comparable search encryption scheme which can support range queries.Then for the demanding of practice,we also improve the basic scheme to make it support multi-clients.We achieve this by leveraging the secret sharing scheme to distribute partial private keys to the service user and then combining them with a random key selected by the user.The private keys generated in our work have two functions.On the one hand,the clients can use their private keys to encrypt the data and generate tokens for the keywords needed to search.On the other hand,with this private key setting,the data owner can also authorize another client to query the expected data in her domain by sending the authorized clients a search capability.With this search capability,the authorized clients can compute the search token for those data encrypted by authorizer.Finally,we also conduct a series of experiments to show that our comparable searchable encryption scheme is available and efficient enough to support daily use.

Related work.Searchable encryption [Bellare,Boldyreva and O’Neill (2007)] has been the focus of scholars since its generation.Comparable encryption [Furukawa (2013)],as an important part of searchable encryption,was first proposed by Furukawa,and has provided a sorting encryption method.Unlike the traditional order-preserving searchable scheme [Boldyreva,Chenette,Lee et al.(2009)],comparable encryption scheme aims at providing a conditional order-preserving encryption scheme that requires authorization.That is to say,only the authorized user can learn the order of the encrypted data.At that time,a concept called order-revealing encryption scheme [Lewi and Wu (2016)] was also underway,and its appearance was also to eliminate the drawbacks of the traditional OPE schemes.And since then,more and more programs have been proposed to meet the needs of the application,which mainly moves in two directions,one is functional design and the other is safety analysis [Grubbs,Sekniqi,Bindschaedler et al.(2017)].For example,Ye et al.[Ye,Miao,Chen et al.(2018)] effort to extend the basic comparable encryption to support multi-user and Furukawa improved their original scheme to make it more efficient with small storage overhead.However,their improvements also have some unsolvable problems,our work in this paper is just to optimize the existed schemes and attempts to achieve a trade-off between the efficiency and functionality.

Organization.The rest of this paper is organized as follows.Section 2 describes the proposed system model,corresponding threat model and design goals.In Section 3 we introduce related background of our scheme and cryptographic protocols.In Section 4,we present our basis scheme and introduce how to extend it to realize multiple clients setting.The formal security proof is given in Section 5 and following with the complexity analysis and experiment evaluation in Section 6.Finally,we end the paper with a brief conclusion in Section 7.

2 Problem statement

2.1 System model

Our target scheme for secure IoT numerical data search involves the following four parties as depicted in Fig.1,i.e.,data terminal equipment (DTE),data sub-management center (DMC),Cloud Server (CS),and a private key generator (PKG).

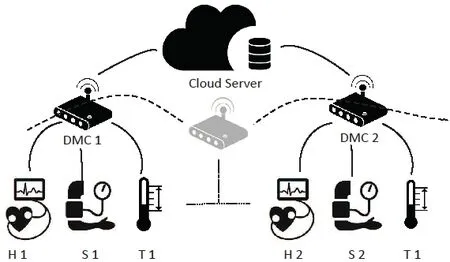
Figure1:Overview of the system architecture

· DMC:DMCs are IoT service provider and data owner.They collect the data from the application or device and encrypt it before uploading it to the cloud server.

· DTE:DTEs are IoT applications or sensor devices (such as heart rate monitor,thermometer and sphygmomanometer,etc.) that serve as data sources or data sink.They detect events or changes in its environment and send the information to the data management center.

· CS:CS is the cloud service provider,it stores all the data and helps perform encrypted data query.

· PKG:PKG is just like an authority center who is responsible for generating system parameters and deriving the private key for each DMC.

Overview.The overview of our scheme is illustrated in Fig.1.Without loss of generality,taking medical scenarios as an example,our system framework and functional module descriptions are described below.When a DMC wants to interconnect with our datastore to get the system service,it sends the registration application and get a partial key as the response from the PKG.Observe that,in our scheme each DMC (doctor) has multiple DTE (devices) such as heart rate monitor,thermometer and sphygmomanometer,these devices collect the data from the patients and import it to data sub-management center.DMC encrypts the received data and uploads them to the cloud.While a DMC wants to filter the eligible data (For instance,medical records with a body temperature greater than 36°C) that satisfies appropriate conditions,she can generate a search token and send the token along with the query to the cloud server.Once the cloud server receives the query and corresponding token,it executes search algorithm to match the eligible data and returns the search results to the DMC.Furthermore,our system also supports multi-user data sharing to utilize their data,i.e.,while a userDiwould like to exploit the medical data of another userDj,to help her analyze the patient’s condition,Dican apply for the authorized search capability,a conversion key,from the data ownerDjby negotiating or paying a certain fee.Then she can use this conversion key to compute the token which can be used to compare with the data ofDj.

2.2 Threat model

Considering the confidentiality and privacy of medical data,we are concerning on the semi-honest threat model including legal users who are curious but not malicious.In our system,we assume that the PKG will never reveal her master secret key to the unauthorized user even the cloud server.Furthermore,the user’s private keys also should be kept secret and cannot be stolen by attackers.The service server in the designed system is honest and takes action according to the rules.

2.3 Design goals

The designed MCSE system over encrypted IOT data should achieve the following main security,functionality and performance goals.

·Data and query privacy:The privacy of the data stored in the datastore must be guaranteed,that is,the cloud server cannot learn any underlying information except the encrypted data and query themselves.

·Comparability of encrypt data:The encrypted data stored in our MCSE datastore can be compared to the size through an authorized token.

·Scalability and efficiency:To enhance the practice of the proposed comparable encryption,our system is also required to support multi-user.With the authorization of the data owner,users can search the target data through our comparable encryption schemes.

3 Preliminaries

3.1 Bilinear pairings

Definition 3.1.Let G1,G2be two cyclic groups with the same prime orderp,andgbe a generator ofG.Lete:G1×G1→G2be a map from G1to G2.We say that the mapeis cryptographic bilinear if the following three properties hold:

· Non-degeneracy.If G =g,then G2=e(g,g),i.e.e(g,g)≠1,where “1” denotes the unity element of the groupG2.

· Computability.For allg1,g2∈G1,there exists an efficient polynomial time algorithm to computee(g1,g2).

For reducing the security of our scheme to a standard hard math problem formally,some classical hardness assumptions and technique are needed to be introduced in our paper,such discrete logarithm problem,secret sharing problem.

3.2 Comparable searchable encryption and security definitions

According to the description above and some related works,the definition of our designed comparable search encryption scheme can be described as follows:

Definition 3.2.The proposed Comparable search encryption scheme with multi-user consists of the following four functions and proceeds as follows:

· Setup:This algorithm takes the security parameterλand range parametersnas input,outputs the system parametersspand master secret keymsk.

·Derive:This algorithm takesmskas input,and generates a partial private keysk1to the user,then user chooses a randomsk2and setssk=(sk1,sk2)be her private key.

·Encrypt:This algorithm takes data owner's private key,system parameters and numeric datamas input,and outputs the ciphertextEmi.

·TokGen:This algorithm takes data owner's private key and expected keyworddas input,and outputs the search tokenTd.

·Compare:This algorithm takes the search tokenTd1,ciphertextEd1and another ciphertextEd2as input,outputs -1,0,1.Here -1meansd1＜d2,0meansd1=d2,1 meansd1＞d2.

From the definition,we know that comparable searchable encryption scheme provides an approach to perform ranger query,i.e.,search a data set which is smaller/bigger than some certain values.Then for the security,we introduce a IND-CKA security game between the adversary and the simulator in the absence of a token,which is defined as follows:

Definition 3.3For a given security parameterλand a range parameterN,letΣ=(Setup,Derive,Encrypt,TokGen,Compare) be a comparable search encryption scheme.Assume thatA = (A1,… ,Aq)is an adversary who can make at mostqtimes queries and S is a simulator,then the security games proceeds as follows:

We say that a comparable encryption scheme CES=(Setup,Derive,Encrypt,TokGen,Compare) is secure if for any polynomial time adversary can distinguish GameRealand GameIdeal,i.e.,

Pr[RealA(λ)= 1 ]-Pr[I dealA,S(λ)= 1 ] ＜negl(λ)

wherenegl(λ)is a negligible function in security parameterλ.

4 Our construction

Let G1,G2be two cyclic groups with the prime orderpande:G1×G1→G2be a bilinear map from G1to G2.Our MCSE scheme on an IoT scenario as Fig.1 consists of five protocols and can be described as follows:

4.1 System initialization

In the initialization stage, PKG executes as described in Setup protocol in Fig.2.First, it selects a bilinear map e:G1×G1→G2with a randomly generator g∈G1.Then an integern is selected as the range parameters which defines the upper bound of the number that can be compared in our system.This means that our construction enables to compare size for the encrypted data of whose underlying data no more thann .PKG also chooses one cryptographic hash function H:{0,1}*→{0,1}λand three key-based pseudorandom functionwhereλis the security parameter.Random integers a, s ∈Zpare selected as the master secret keymsk in our system.In the derivation stage, PKG solves the equation ax + s = y m odpto find a pair of solution (x, y)to compute the private key for each DMC.Finally, PKG publishes the system parameters sp ={n, g1,H1,H2, H3, e}and keeps msk =(a, s)to itself.

Figure2:Our basic encrypted data search scheme

4.2 Private key derivation

For a data sub-management centerDito be connected to the system, she needs to apply to be a legal user and get a corresponding private key from PKG. As described in Derive protocol in Fig. 2, PKG choosesx,y∈Zprandomly, which satisfiesy=ax+sm odp.Then it computes the's partial private key (gx,gy)and sends it toAfter receiving the partial key from PKG,randomly chooses an integert∈Zpand compose its own private key(gx,gy,t)with them. In the following Encrypt and Search protocols,will use the obtained private key to encrypt the data which is imported by various devices(heart rate monitor, thermometer and sphygmomanometer) under its jurisdiction, and compute search token to perform received query.

4.3 Encrypted comparable datastore generation

For each DTE,we present the generation of the encrypted comparable datastore by Encryption protocol in Fig.2.Note that,all data in our system should be an integer or can be converted to an integer by a certain mapping that means the original data in our scheme can be compared in size.Our goal is to ensure that the encrypted data stored in datastore not only reveals its underlying information,but also can compare size with each other by a given search token.Take a medical scene as an example,in our system,each device collects the data (body temperature,heart rate) from patient and aggregates it to a DMCDiwho may be an attending physician.

As shown in Fig.2,to keep the privacy of the data,next we will describe how to encrypt an integermby Encrypt protocol.First,Diconvertsmto its binary form (b0,… ,bn-1)which satisfiesA random variabler∈Zis selected to guarantee the randomness of encrypted data.Then forifromn-1to1,PKG computesdi+1andeiin turn,wheremod2andH2(Ks,di+1) +bimod3.The last step in Encrypt protocol is to compress to get a short ciphertextE,whereLater,uploads all encrypted data to the cloud server.Unlike ordinary order-preserving encryption scheme,our encrypted data will not reveal the order of the plaintext while protecting data privacy.The only thing she will know is the size relationship of the ciphertext and the data that corresponds to the given token.

4.4 Token generation and multi-client setting

The last functional module of our system is the comparable search over encrypted data which is generally composed of two protocols,token generation and search.For example,when a doctor wants to search for the medical record of the patients whose temperature is greater thand°C to analyze the condition,she needs to compute a token fordand send it to the server.Then the server helps her to complete the search operation and returns the search result.Considering that the token generation protocol in our system will vary depending on the target database,we separate this part into a section and elaborate on our token generation scheme in different scenarios,i.e.,which data the user wants to query,her own or other data including hers? Combined with Fig.1 and different scenes,the token generation protocol TokGen works as follows:

For the first case,if the doctor only wants to search the data of her own which is encrypted by her private key,she just takes her private key and the expected data as inputs and invokes TokGen protocol to compute the search token.As shown in Fig.2,is the binary form of numberd,letThen forifromnto1,DMC calculatesin turn,whereandThe obtained arrayis the search tokenTK.

Note that this token can only be used to compare the size for encrypted data which encrypted with the same private key.For the data encrypted with other keys,it cannot directly compare them.Fortunately,we have an approach to compare the size of data encrypted with different private keys,which is what we will discuss later.

In the case that a doctorDiwants to search for the medical record of more patients whose temperature is greater thand°Cin another hospital, then the search results consist of two parts. One is her own data, this part of the data can be searched directly with token generated by her private key. While the other part of the data comes from another hospital, which cannot be filtered by that token anymore. To solve this problem, we exploit a transformation technique to convert our token into a token that can be compared to the encrypted data of another hospital. LetDi,Djbe two different users with private keyrespectively, whereNow we illustrate this interaction in detail. First,Djsends an application toDifor searching her encrypted data stored in the cloud. In response,calculatesas the conversion key and sends it toThencomputesto get thei.e.,above, which is the key to calculating token forFinally,Djperforms the remaining operations in the TokGen protocol as usual to get a new token, this token can be used to compare withDi’s encrypted data. Observe that, this process of authorized search requires that both users must be legitimate users in the system, they have got the private keys distributed by PKG, and successful authorization requires the consent of the data owner and obtains the conversion key. The entire process requires only one interaction to achieve data sharing with high efficiency.

4.5 Comparable search

The last functional module of our system is the comparable search over encrypted data which is generally composed of two protocols,token generation and search.And the token generation is completed by different participants depending on the situation.As shown in Fig.2,the specific description of the search module is as follows:

If the initiator is the data owner,then she directly computes the search token by calling the TokGen protocol with the inputs of her private key and the expected keyword.Then she takes theas input and performs the search algorithm to retrieve the goal data.Specifically,for the given ciphertextandwhereEis the ciphertext corresponding to the number whose token isTK.The cloud server computesmod3 forkfromnto 0.If there exist a certainksuch thatwe can decideEE′＞andforE＜E′.Otherwise,E=E′if allck=0.Then she collects the data with the calculation results “1” and return them to the user.While the search initiator is not the data owner,she needs to ask for the authorization from the data owner first,and then computes the search token by the later protocol mentioned in the token generation part.After that she can use that token to perform the data search normally.

5 Security analysis

This section we will present the security of our CSE scheme in the following two theorems.For the sake of limited space,we only provide a simple explanation of the security of the solution and no longer give formal proof.

Theorem 5.1.The proposed comparable search encryption scheme CSE= (Setup,Derive,Encrypt,Token,Search) isL -semantic secure ifH:{0,1}*→{0,1}λis cryptographic hash function and{0,1}*→{0,1}λare three key-based pseudo random function.

Since our proposed comparable searchable encryption scheme is constructed based on the work of Furukawa’s [Furukawa (2014)],so the proposed scheme is secure under the security model of Furukawa [Furukawa (2014)].The detailed security proof is to prove that no polynomial adversary can distinguish the security game Ideal and Real which will not be detailed here.In addition,as our scheme extends the basic comparable encryption scheme to support multiple users.So the proposed scheme must ensure that the unauthorized user cannot search the data beyond their authority.

Theorem 5.2.Assume that the DL assumption holds and the CSE=(Setup,Derive,Encrypt,Token,Search) is aL -semantic secure scheme,then the search token in our scheme CSE is unforgeable against adaptive attacks.

This theorem ensures that our scheme provides fine-grained access control on encrypted data,only the authorized users can compute the valid tokens to perform search query.In our construction,we achieve this by dividing the private key into two parts,one is assigned by the PKG and the other is an integer selected by the users themselves.Then we exploit the secret sharing technique to distribute the system parameters and hide the selected part by the exponential operation.Then we can know that no polynomial time adversary can fetch this private key,otherwise he can break the DL problem.Furthermore,this setting also weakens the dominance of PKG which guarantees that the user’s key will not be revealed even if someone will eavesdrop on the communication channel.

6 Efficiency analysis and experiment evaluation

In this section,we present our analysis results by making efficiency comparison with some related work,and conduct the corresponding experiment to evaluate its practice.

6.1 Efficiency comparison

To show the efficiency of the proposed scheme in Section 4,we simply analyze the efficiency of our scheme by comparing with some classical comparable searchable encryption scheme.Let |G1|,|G2|,|Zp|respectively be the size of the element ofG1,G2,Zp,letP,E,Hrepresent the computation cost of a bilinear pairing operation,an exponentiation operation on pairing and hash computation cost.Letλandndenote the security and range parameters.Then the detailed comparative analysis is listed in Tab.1.

Table1:Comparison with several classical schemes

6.2 Experiment results

To evaluate the performance of the proposed scheme in Section 4,we will show all the experimental results in this part.In our work,all the experiments are conducted on a Windows 10 laptop with Core i5 Processor,8 GB Memory and 256 GB SSD.Letλ=256be the security parameter andn=128be the range parameter.A synthetic dataset of 10000 integers selected by the range parameter is our test set.Our pairing implementation uses the jPBC library for Java.In addition,we choose SHA256 as hash functionHand AES-CBC encryption mode for key-based cryptography functionH1,H2,H3.Then the detail experiment results are described as follows.

For the user of our system,she needs to register to get an authorized private key.We realize this by running the Derivation protocol as Fig.2.In this stage,we do the experiment of generating private keys for 1000 users.The mainly computation overhead is two exponential operations and some additions and subtractions on a selected finite fields.Fig.3(a) shows the time cost for 1000 users.From the figure we can see that it takes about 29.3 s for total 1000 users and 29.3 ms per user.Fig.4(a) demonstrates that almost 99% of tests can complete key generation in 5 seconds.

Figure3:Performance of private key deriving and encryption

Figure4:Performance of private key deriving,encryption and encrypted data search

For a synthetic dataset DS consists of 10,000 integers from 0 to 2128,we take valid private keys generated above to encrypt the DS by performing Encrypt protocols.The line in Fig.3(b) shows the time cost of encrypt total dataset.In addition,we also record the time for each integer.It takes about 3-5ms to encrypt each data,which is much faster than the results in Ye et al.[Ye,Miao,Chen et al.(2018)].

While for the search stage,we randomly choose a integer “d” from the dataset DS randomly,then perform the search protocol to find out the record whose underlying value is bigger than “d” from the encrypted dataset EDS.Fig.4(b) records the time cost of retrieving all the data which is bigger than “d”,it takes about 594 ms to return all the search results,i.e.,each search test only cost 0.059 ms in our construction.

7 Conclusion

In this paper we discuss the encrypted data search problem in cloud and provide a multiclient comparable searchable encryption scheme which gives a solution for encrypted data sharing and retrieve.Compared with related schemes,our scheme improves efficiency of the key distribution process by adopting a modified secret sharing technique.This paper also gives detailed experimental results of the scheme and demonstrates that it can adapt to current application requirements.For future work,it is interesting to consider the searchable encryption with multi-keywords and small leakage.

Acknowledgement:This work is partially supported by the Fundamental Research Funds for the Central Universities (Nos.30918012204,XJS17053,JBF181501).The authors also gratefully acknowledge the helpful comments and suggestions of the reviewers,which have improved the presentation.