海洋新区政策对沿海地区经济效率的影响研究——以舟山海洋新区为例

郑 奕，刘观园

（上海海洋大学 a.信息学院；b.经济管理学院，上海 201306）

引 言

为了促进改革开放，优化产业布局，提高经济发展的质量和效益，我国实施了设立国家级新区的战略。国家级新区是由国务院批准设立，承担国家重大发展和改革任务的国家级综合功能区，其担负着带动区域经济发展、引领全面改革开放、推动体制机制创新、促进产城融合和城乡一体发展等方面的重要职责。随着国家级新区设立的数量不断增加，适时对已建成的国家级新区促进地区经济发展的质量进行评估，有利于在高速度向高质量经济发展的转型中，为其他新区的建设提供借鉴，进一步提高经济发展效益。

2011年6月，国务院正式批准设立浙江舟山群岛新区，舟山成为首个以海洋经济为主题的国家级新区，新区范围与舟山市行政区域一致，总面积为2.22万平方公里，其中海域面积达2.08万平方公里。舟山陆域面积小，海域面积大，海洋经济是其经济发展的重点。因此，舟山群岛新区的设立是我国一项重要的海洋经济战略决策。客观评估该政策能否有效促进舟山经济发展，不仅有利于分析其在地区经济发展中的作用，探索沿海地区的经济发展模式；还有利于促进舟山成为浙江海洋经济发展的先导区和长三角地区海洋经济发展的重要增长极，推动我国海洋经济的进一步发展。

关于舟山新区的研究已有很多。在经济建设方面，研究在以下三个方面比较集中。首先是关于经济发展战略方面的研究：如易开刚（2014）依据经济地理学中的“极化效应”理论，提出了提升舟山群岛新区极化效应的战略协同机制、空间优化机制、要素集聚机制和沟通协调机制[1]。郭力泉等（2015）以舟山市科技统计数据为基础，研究认为海洋科技进步是引领舟山群岛新区建设发展的重要基础和核心动力，并提出了舟山群岛新区实施创新驱动发展的战略[2]。其次是关于具体产业或项目的经济研究：如汪自书等（2013）从港口物流、修造船、水产品加工和海洋旅游等角度提出了未来的产业发展路径[3]。王文佳等（2013）对新区发展航运金融服务业进行分析，提出了新区航运金融服务体系的基本架构[4]。崔松岩（2014）从舟山群岛新区港口物流信息化建设现状及存在的问题入手，提出了舟山港口物流信息化建设的保障措施[5]。第三方面是通过和其他地区的比较来分析舟山的优势和不足：如范巧等（2017）考察了成立5年以上的浦东、滨海、两江、舟山群岛4个国家级新区辐射带动中国各省份发展的能力状况，认为舟山群岛新区已基本形成区域增长极[6]。彭勃（2013）则通过比较舟山、宁波、上海三个港口的区位势，提出了舟山群岛新区港口发展思路及相应的保障措施[7]。

上述研究对舟山经济的发展提出了很多有益的建议，但这些研究在理论上的定性分析较多，量化分析的实证研究较少。尤其是关于新区的设立是否促进了舟山经济增长的质量的相关实证研究在已有报道中很少看见，而其又是经济新常态下进一步推动地区经济发展所需解决的重要问题。由于“在国家层面上，‘竞争力’的唯一含义就是国家的生产效率”，而国家生产效率又主要反映在节点城市和大城市的生产效率上[8]。因此分析城市经济效率可以反映该地区的经济发展质量。故本文拟从经济效率角度研究国家新区政策是否有效地提高了舟山经济发展的质量，以便于为我国沿海地区经济发展进一步的战略规划提供借鉴。为此，本文创造性地将数据包络分析与反事实分析两种研究方法相结合，主要研究思路是：以舟山市为实验组，选择与其行政级别相近的江浙皖部分地级市作为控制组，首先利用1995-2015年的经济数据，运用数据包络分析理论量化评价上述城市自1995-2015年的经济效率，然后运用反事实分析方法实证研究新区政策对舟山经济效率的影响。

1 方法与数据

1.1 方法的选取

评估舟山群岛新区成立对舟山经济的影响，理论上可以选取影响新区经济因素指标，建立回归模型后进行评估。常用的基于回归的评估政策效应的方法有联立方程组模型、VAR模型以及DSGE模型，然而，这些方法都有诸多严格的假定，使用起来并不容易。例如，联立方程组模型依赖于变量先验的外生性和内生性假定，VAR模型则存在变量维数限制和经济机理解释的困难。

鉴于此，经济学家们将准实验方法应用于宏观政策评价中。准实验方法将项目、政策视为一项实验，试图在精心设计的实验条件下，为实验组找到一个自然产生的对照组。准实验方法包含工具变量（instrumentalvariables，IV），双重差分（DID），以及断点回归（RD） 等方法。但上述方法都有其各自局限性，如DID法必须满足随机性假设，即必须通过随机化排除那些无法控制因素的影响，从而控制所有可能影响实验结果的无关因素；同时还需具备同质性假设，即实验组和控制组的样本除实验者所操纵的实验变项（政策冲击）不同外，其余各方面都应达到近乎相等或完全相似的程度。为改进这些方法，Hsiao等（2010） 提出了一种基于面板数据的衡量政策效应的新方法，它利用面板系统各截面之间因共同驱动因子而产生的联系构建实验组个体的“反事实”。一方面，此方法认为经济系统的一些共同因子驱动着截面上各个体的经济运行，虽然它们的影响程度不同，但在截面上具有一定联动性或相关性，故可由政策发生前实验组和控制组相关关系的估计来预测政策发生后实验组的“反事实”，从而放松DID法必需的随机性假设。另一方面，此方法可克服宏观政策评价中存在的因果关系不明确、理论建模复杂、遗漏变量、时间序列数据不足等困难，一定程度上可降低变量选择与估计方法对实证结果稳健性的干扰。

尽管基于面板数据的反事实分析方法提出时间不长，但已经在政策效应评估上得到很多应用。利用此方法，Hsiao等（2010） 使用由24个国家组成的控制组来评估香港回归大陆后的政治和经济一体化的影响[9]。Ching等（2011）则评估了中国加入世贸组织的影响[10]。赵捷等（2017）依据中国与中巴经济走廊沿线贸易伙伴国的贸易数据，测算了中巴经济走廊贯通将造成的经济效应[11]。谭娜等（2015），殷华等（2017） 和王利辉等（2017） 分别对上海自贸区对上海经济的增长效应和上海自贸区产生的“制度红利”等进行了评估[12-14]。这些研究，使反事实方法在宏观政策绩效评价中的适用性得到了充分的验证。基于此，本文选择利用“反事实”方法探究设立舟山群岛新区的政策对舟山地区经济效率的影响。

1.2 指标与数据

“反事实分析”方法要求所收集的数据截面须满足政策实施前时期长于政策实施后时期。考虑到舟山群岛新区2011年6月正式设立，且在2010年5月国务院已提出“建设浙江舟山海洋综合开发试验区”规划，故本文收集1995-2010年的16年数据反映舟山群岛新区设立前的经济状况。又考虑到2015年12月，国务院批准在舟山设立大宗商品交易中心——中国（浙江）大宗商品交易中心，为避免该因素干扰对新区设立的经济影响的分析，故本文以2011-2015年的5年数据反映新区设立后的经济状况，这样收集的数据既能充分满足反事实分析的要求，又有利于减少新区设立之外的其他因素的干扰。

Hsiao等（2010） 认为经济发展中存在着一些公共因子驱动着截面上的各个个体，这些因子对每个个体的影响程度不同，但却使得截面之间具有某种相关性。如影响经济增长的因素（人口、资本、技术等）一般在地区范围内存在共性，尽管这些公共因子对各地区经济发展的作用程度不同，但他们的存在使得各地区的经济具有相关性[9]。基于上述思想，为在研究新区设立对舟山地区经济的影响时，将这些公共因子的作用分离出去，本文将设立新区的舟山作为接受政策实验的个体构成实验组，并选择与舟山地缘相近，文化相亲，行政体制均为地级市的部分长三角城市构成新区政策实验中的控制组。控制组中的城市，既有位于与舟山临近的沿海地区，也有位于内陆地区的；既有经济发达城市，也有欠发达城市。本文认为经济大环境对这些城市的影响和对舟山市的影响具有相关性。

关于控制组中城市的选择原则，首先是要能完整获取1995-2015年间所需的经济数据。一些城市由于在本文分析的21年间行政区划发生变化而被剔除。如2011年安徽省撤销地级巢湖市，并将其所辖的一区四县行政区划分别划归合肥、芜湖、马鞍山三市管辖。为避免由于行政区划变化而产生的相关城市经济数据在统计上的变化，对照组中将巢湖、合肥、芜湖和马鞍山四个城市予以剔除。其次，根据Hsiao等（2012） 的假定[15]，要求所选城市的经济变化与舟山群岛新区设立的政策实施相互独立，也就是说控制组中地区变量的选择要使得本地区与舟山经济联系较小。根据舟山经济往来信息及地理位置的周边情况，排除了上海、杭州、宁波、嘉兴、绍兴、台州6个地区。最后，本文选择南京、无锡、常州、苏州、南通、连云港、盐城、扬州、镇江、温州、湖州、金华、衢州、蚌埠、淮南、淮北、铜陵、安庆、黄山、滁州等20个城市组成控制组。首先计算包含舟山市在内的这21个地级城市的经济效率，然后利用计算结果进一步分析新区政策对舟山经济效率的影响。

2 效率分析

本节对上文选定的江浙皖21个地级市的经济效率进行测算，其结果既为下文从效率的角度进行反事实分析做准备，也有助于这些地区通过经济效率的评价及时发现和改进不足，促进要素资源在空间的合理组织和配置，提高区域治理能力和经济发展的质量。

2.1 超效率DEA模型

DEA （data envelopment analysis，DEA） 方法以其适用于多投入和多产出数据的优势，在效率评价方面得到了广泛应用。DEA方法由Charnes等（1978） 提出，旨在评价“多投入多产出”模式下决策单元间的相对有效性[16]。在DEA模型中，如果出现多个决策单元（DMU） 同时有效，即都有效率值θ=1，那么该方法就不能对有效的DMU进行进一步的评价。于是，Anderson等（1993） 创立了超效率DEA模型[17]。超效率DEA模型和传统DEA模型的差别在于：在对某DMU进行效率评价时，先将该DMU排除在生产可能集之外。因此在测评时，就无效的DMU而言，生产前沿面同传统DEA模型一致，该DMU最终效率值与用传统DEA模型测量出来的一样；但就有效DMU而言，生产前沿面同传统DEA模型相比可能后移，这时其测定出的效率值就可能大于利用传统DEA模型测定的最有效效率值1。超效率DEA模型能对传统有效前沿面上的评价对象进一步评价，辨别传统DEA模型中有效DMU之间的差异，并对其进行有效排序。它克服了传统DEA模型无法对多个有效决策单元做出进一步评价和比较的缺陷，因而该模型较传统DEA模型得到了更广泛应用。对决策单元q（q=1，2，…，n），超效率DEA模型可表示为：

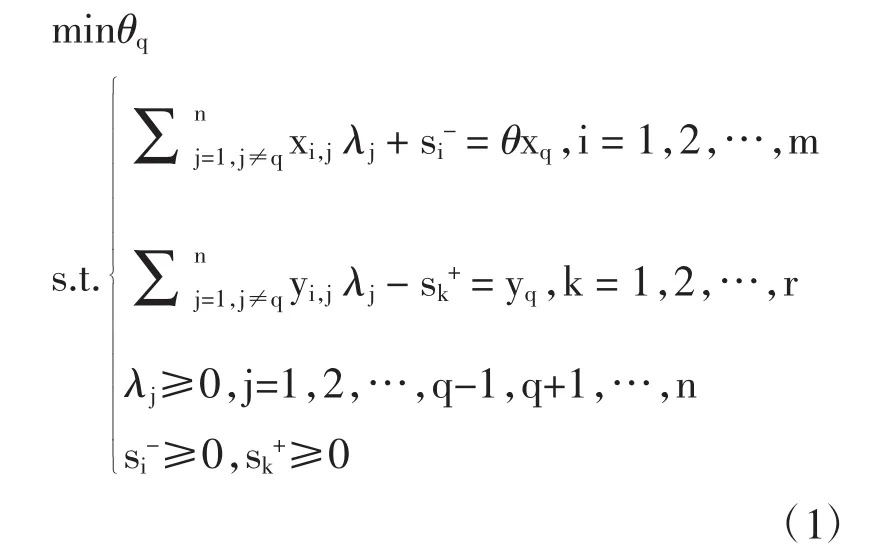
式中θ表示决策单元的效率值，x和y分别为输入和输出变量，λ表示有效DMU中的组合比例，且Σλ＞1，Σλ=1和Σλ＜1分别表明规模收益递增、规模收益不变和规模收益递减；n为决策单元的数量；m和r分别为投入和产出变量的个数。和均为松弛变量，分别为投入超量和产出亏量，即分别表示投入过多和产出过少。当θ＜1时，则表明决策单元非有效，需要改进。当θ大于或等于1，则决策单元都处于传统DEA模型中的有效状态，但可以按数字由大到小进一步对他们的有效状态进行排序。

2.2 江浙皖21个地级市经济效率分析

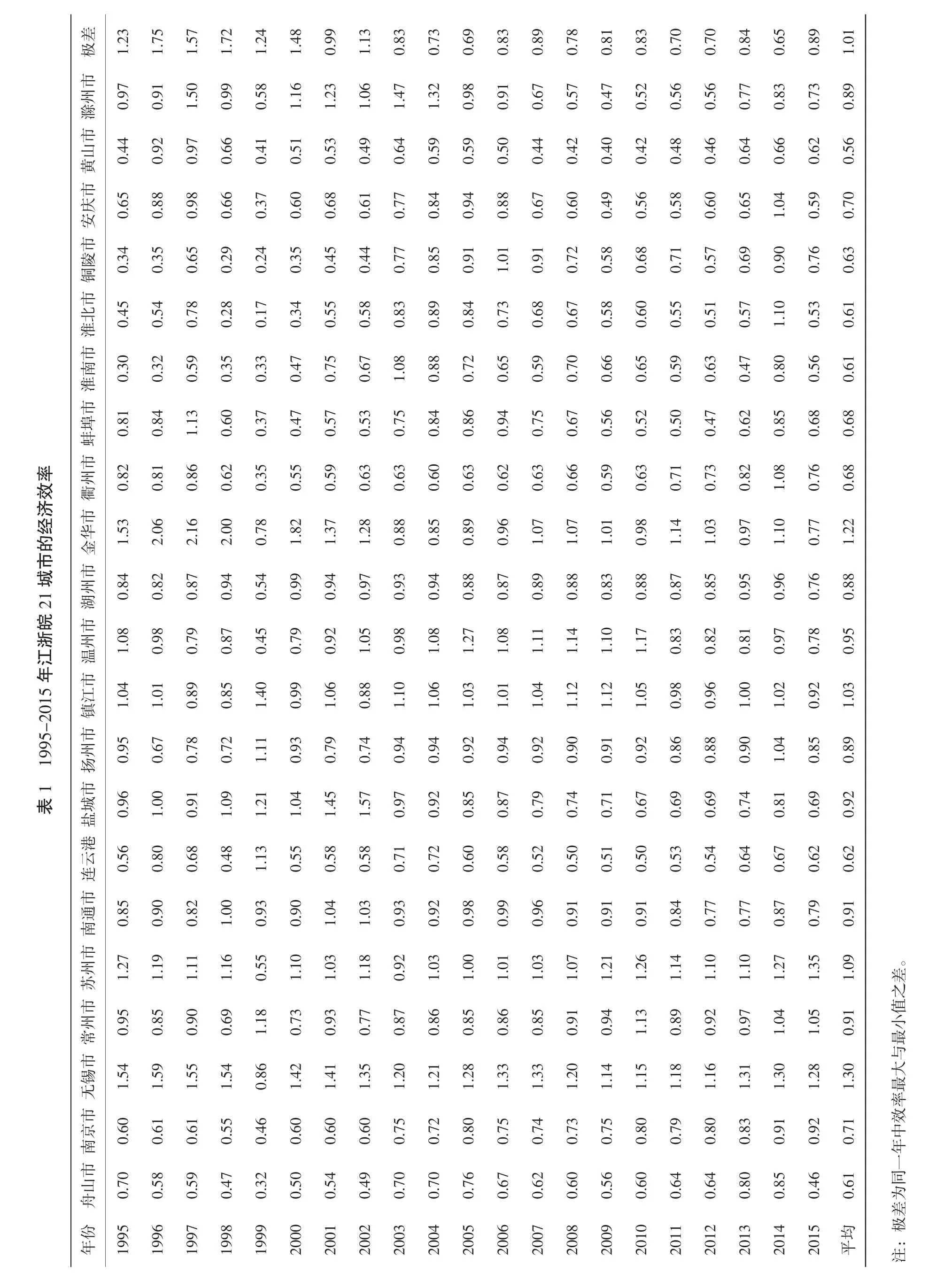
以城镇单位从业人员期末人数，行政区域土地面积，公共财政支出和固定资产投资为四项投入要素指标，以地区生产总值作为产出要素指标，从1996-2016年的《中国城市统计年鉴》中收集了舟山，以及南京、无锡、常州、苏州、南通、连云港、盐城、扬州、镇江、温州、湖州、金华、衢州、蚌埠、淮南、淮北、铜陵、安庆、黄山、滁州共21个城市1995-2015年的相关数据共2 205个（限于篇幅，不在文中列出），利用式1所示的超效率模型，借助EMS软件，计算得到上述21个城市的21年间的经济效率（见表1）。

率效济经的市城2 1皖浙江年5 0 1 2-9 5 1 9 1表差极市州滁市山黄市庆安市陵铜市北淮市南淮市埠蚌市州衢市华金市州湖市州温市江镇市州扬市城盐港云连市通南市州苏市州常市锡无市京南市山舟份年1.2 3 0.9 7 0.4 4 0.6 5 0.3 4 0.4 5 0.3 0 0.8 1 0.8 2 1.5 3 0.8 4.0 8 1.0 4 1.9 5 0.9 6 0.5 6 0.8 5 0.2 7 1.9 5 0.5 4 1.6 0 0.7 0 0 9 9 5 1 5 1.7 0.9 1 0.9 2 0.8 8 0.3 5 0.5 4 0.3 2 0.8 4 0.8 1 2.0 6 0.8 2.9 8 0.0 1 1.6 7 0.0 0 1.8 0 0.9 0 0.1 9 1.8 5 0.5 9 1.6 1 0.5 8 0 9 9 6 1 7 1.5 0 1.5 0.9 7 0.9 8 0.6 5 0.7 8 0.5 9 1.1 3 0.8 6 2.1 6 0.8 7.7 9 0.8 9 0.7 8 0.9 1 0.6 8 0.8 2 0.1 1 1.9 0 0.5 5 1.6 1 0.5 9 0 9 9 7 1 2 1.7 9 0.9 0.6 6 0.6 6 0.2 9 0.2 8 0.3 5 0.6 0 0.6 2 2.0 0 0.9 4.8 7 0.8 5 0.7 2 0.0 9 1.4 8 0.0 0 1.1 6 1.6 9 0.5 4 1.5 5 0.4 7 0 9 9 8 1 4 1.2 0.5 8 0.4 1 0.3 7 0.2 4 0.1 7 0.3 3 0.3 7 0.3 5 0.7 8 0.5 4.4 5 0.4 0 1.1 1 1.2 1 1.1 3 1.9 3 0.5 5 0.1 8 1.8 6 0.4 6 0.3 2 0 9 9 9 1 1.4 8 1.1 6 0.5 1 0.6 0 0.3 5 0.3 4 0.4 7 0.4 7 0.5 5 1.8 2 0.9 9.7 9 0.9 9 0.9 3 0.0 4 1.5 5 0.9 0 0.1 0 1.7 3 0.4 2 1.6 0 0.5 0 0 0 0 0 2 9 0.9 1.2 3 0.5 3 0.6 8 0.4 5 0.5 5 0.7 5 0.5 7 0.5 9 1.3 7 0.9 4.9 2 0.0 6 1.7 9 0.4 5 1.5 8 0.0 4 1.0 3 1.9 3 0.4 1 1.6 0 0.5 4 0 0 0 1 2 3 1.1 6 1.0 0.4 9 0.6 1 0.4 4 0.5 8 0.6 7 0.5 3 0.6 3 1.2 8 0.9 7.0 5 1.8 8 0.7 4 0.5 7 1.5 8 0.0 3 1.1 8 1.7 7 0.3 5 1.6 0 0.4 9 0 0 0 2 2 3 0.8 1.4 7 0.6 4 0.7 7 0.7 7 0.8 3 1.0 8 0.7 5 0.6 3 0.8 8 0.9 3.9 8 0.1 0 1.9 4 0.9 7 0.7 1 0.9 3 0.9 2 0.8 7 0.2 0 1.7 5 0.7 0 0 0 0 3 2 3 0.7 2 1.3 0.5 9 0.8 4 0.8 5 0.8 9 0.8 8 0.8 4 0.6 0 0.8 5 0.9 4.0 8 1.0 6 1.9 4 0.9 2 0.7 2 0.9 2 0.0 3 1.8 6 0.2 1 1.7 2 0.7 0 0 0 0 4 2 9 0.6 0.9 8 0.5 9 0.9 4 0.9 1 0.8 4 0.7 2 0.8 6 0.6 3 0.8 9 0.8 8.2 7 1.0 3 1.9 2 0.8 5 0.6 0 0.9 8 0.0 0 1.8 5 0.2 8 1.8 0 0.7 6 0 0 0 5 2 3 0.8 0.9 1 0.5 0 0.8 8 1.0 1 0.7 3 0.6 5 0.9 4 0.6 2 0.9 6 0.8 7.0 8 1.0 1 1.9 4 0.8 7 0.5 8 0.9 9 0.0 1 1.8 6 0.3 3 1.7 5 0.6 7 0 0 0 6 2 9 0.8 0.6 7 0.4 4 0.6 7 0.9 1 0.6 8 0.5 9 0.7 5 0.6 3 1.0 7 0.8 9.1 1 1.0 4 1.9 2 0.7 9 0.5 2 0.9 6 0.0 3 1.8 5 0.3 3 1.7 4 0.6 2 0 0 0 7 2 8 0.7 7 0.5 0.4 2 0.6 0 0.7 2 0.6 7 0.7 0 0.6 7 0.6 6 1.0 7 0.8 8.1 4 1.1 2 1.9 0 0.7 4 0.5 0 0.9 1 0.0 7 1.9 1 0.2 0 1.7 3 0.6 0 0 0 0 8 2 0.8 1 0.4 7 0.4 0 0.4 9 0.5 8 0.5 8 0.6 6 0.5 6 0.5 9 1.0 1 0.8 3.1 0 1.1 2 1.9 1 0.7 1 0.5 1 0.9 1 0.2 1 1.9 4 0.1 4 1.7 5 0.5 6 0 0 0 9 2 3 0.8 0.5 2 0.4 2 0.5 6 0.6 8 0.6 0 0.6 5 0.5 2 0.6 3 0.9 8 0.8 8.1 7 1.0 5 1.9 2 0.6 7 0.5 0 0.9 1 0.2 6 1.1 3 1.1 5 1.8 0 0.6 0 0 0 1 0 2 0 0.7 6 0.5 0.4 8 0.5 8 0.7 1 0.5 5 0.5 9 0.5 0 0.7 1 1.1 4 0.8 7.8 3 0.9 8 0.8 6 0.6 9 0.5 3 0.8 4 0.1 4 1.8 9 0.1 8 1.7 9 0.6 4 0 0 1 1 2 0 0.7 6 0.5 0.4 6 0.6 0 0.5 7 0.5 1 0.6 3 0.4 7 0.7 3 1.0 3 0.8 5.8 2 0.9 6 0.8 8 0.6 9 0.5 4 0.7 7 0.1 0 1.9 2 0.1 6 1.8 0 0.6 4 0 0 1 2 2 0.8 4 0.7 7 0.6 4 0.6 5 0.6 9 0.5 7 0.4 7 0.6 2 0.8 2 0.9 7 0.9 5.8 1 0.0 0 1.9 0 0.7 4 0.6 4 0.7 7 0.1 0 1.9 7 0.3 1 1.8 3 0.8 0 0 0 1 3 2 5 0.6 0.8 3 0.6 6 1.0 4 0.9 0 1.1 0 0.8 0 0.8 5 1.0 8 1.1 0 0.9 6.9 7 0.0 2 1.0 4 1.8 1 0.6 7 0.8 7 0.2 7 1.0 4 1.3 0 1.9 1 0.8 5 0 0 1 4 2 0.8 9 0.7 3 0.6 2 0.5 9 0.7 6 0.5 3 0.5 6 0.6 8 0.7 6 0.7 7 0.7 6.7 8 0.9 2 0.8 5 0.6 9 0.6 2 0.7 9 0.3 5 1.0 5 1.2 8 1.9 2 0.4 6 0 0 1 5 2 1 1.0 9 0.8 0.5 6 0.7 0 0.6 3 0.6 1 0.6 1 0.6 8 0.6 8 1.2 2 0.8 8.9 5 0.0 3 1.8 9 0.9 2 0.6 2 0.9 1 0.0 9 1.9 1 0.3 0 1.7 1 0.6 1 0均平。差之值小最与大最率效中年一同为差极：注

表1计算结果显示，21个地级市从地域分布看，无锡、苏州、金华和镇江市的平均效率较高，均大于1；从时间序列看，每年最高和最低效率间的极差有缩小的趋势。如1995-2000年间的效率极差均超过了1.2，而2003-2015年的13年间，极差均不超过0.89。鉴于DEA理论中效率的相对性，这个现象说明近些年长三角经济一体化发展促进了要素的合理配置，避免了经济效率上的两极分化。同时也注意到，舟山市的经济效率在这些城市中一直处于相对较低水平，需要评估舟山群岛新区政策对舟山市的经济效率的促进作用。

3 设立新区的经济效应分析

虽然由表1可见，舟山群岛新区设立（2011年）后舟山地区经济超效率值仍然呈现波动变化，但这并不能说明舟山群岛新区政策对舟山经济效率的影响。因为经济效率是多种因素共同作用下经济变化的结果，新区政策的实际作用还需要通过从其他影响因素中分离出来后进行分析。

3.1 理论模型构建

设研究时期从t=1期到t=T期，研究涉及的全部城市为N个，是yit舟山（i=1） 和其他N-1个城市（i=2，3，…，N） 的经济效率指标。由于影响一个地区经济效率的因素除了有该地区的特殊效应，也有经济大环境中的许多公共因子，如人口、资本、技术等，虽然这些因子对不同地区的影响程度不同，但在时间截面上具有一定的相关性，因此各城市经济效率可由如下因子（因子可能是多个且未知的）模型表示：

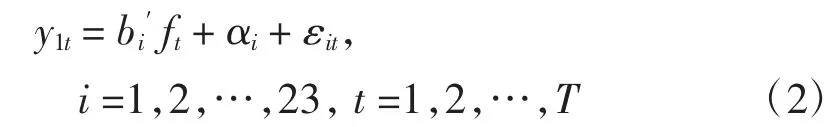
其中ft（K×1） 为K维随时间t变化的影响经济效率的公共因子向量，（K×1） 是K维随地区i变化的系数向量，αi是地区i的固定效应，εit是随机扰动项，满足。E（εit）=0。记为i城市第t年时没有受舟山群岛新区设立经济影响的城市的经济效率，而是受新区设立经济影响的i地区第t年时的经济效率。若以舟山群岛新区设立前的2010年为T1期，当新区无论成立与否对该城市的经济效率yit均没有影响时，则：

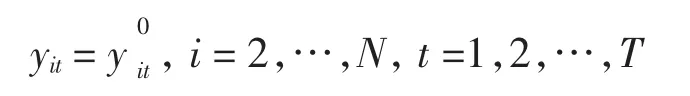
若新区成立前对舟山经济效率无影响，成立之后有影响，则

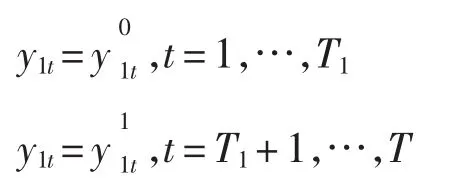
若定义虚拟变量dit：dit=1表示i地区在t时期的经济效率受政策干预，dit=0表示其未受政策干预。则i地区第t年时的经济效率一般的可表示为：

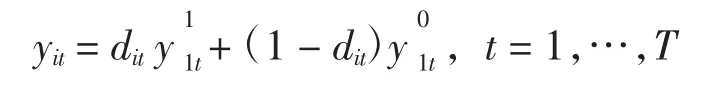
这里假设舟山市以外的其他N-1个城市的地区宏观经济增长特有的随机构成成分与政策干预变量dit是条件独立的，即

由于（2） 式中ft在宏观经济中不易观察，“反事实分析”方法建议在研究期内利用代替ft来拟合y1t。现令舟山群岛新区设立后影响舟山经济效率y1t的处理效应 Δ1t为但由于在时间T1后实际上是观测不到的，因此无法直接计算Δ1t。为此，“反事实分析”方法认为，面板系统截面上不同个体之间由于共同因子的作用，互相之间存在联系，故当政策在T1年发生后，可利用未受到政策干预的对照组的信息来预测假设政策未发生时实验组个体在T1+1，…，T时期内的宏观经济指标。即首先在t=1，2，…T1，时期内，利用实际观察到的时间序列数据代替（2） 式中的ft来拟合得到拟合值，通过不同回归结果的比较，在对照组中恰当地选择M个城市组成控制组，形成最优拟合：

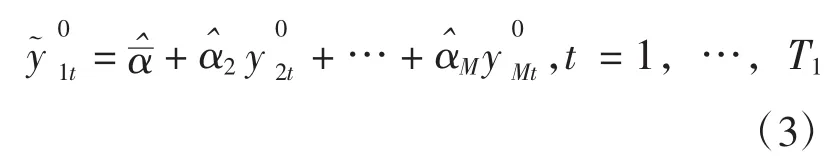
然后利用控制组的实际观察值，根据（3）进行的样本外预测，推出实验组个体在t=T1+1，…，T时期内的宏观经济指标的“反事实”值。即：

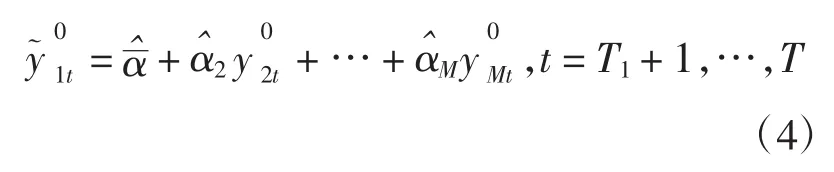
根据上述反事实分析的理论，由于可以认为前文选择的20个未受到新区政策干预的地级市在同一时期的经济效率都受到和舟山市相同的共同因子的影响，尽管这些共同因子对各个地区经济发展的驱动程度不同，但导致了时间截面上各城市经济数据之间存在相关性，因此可以利用这20个未受到新区政策干预的地级市构成的控制组的信息来推测若新区政策未发生时的舟山市2011年后的“反事实”的经济效率。

由（4） 式推出的T1+1年后的反事实的地区生产总值，可得舟山新区设立后影响舟山地区生产总值指标的处理效应Δ1t的估计如下：

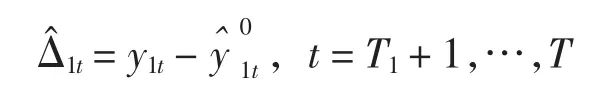
Hsiao等证明[15]式（5） 是实际处理效应Δ1的一致性估计。模拟结果显示，上述预测方法得到的处理效应的误差较小，且小样本表现更优。因此在式（3）的拟合分析中，可以只挑选面板数据中的部分个体作为控制组来构建受政策影响个体的“反事实”值。实际操作中，控制组有多种选取方法，本文按照Hsiao[9]的方法，采用如下选择策略：

第一步，对实验个体外的N-1个个体，选任意固定的j（j=1，2，…，N-1），在N-1个截面单位中任意挑出j个个体，共可得到种控制组。用实验个体的经济效率指标和各控制组中j个城市的经济效率指标拟合，得出反事实值表达式（3） 式，根据Akaike信息准则（AIC）选出对（t=1，…，T1）拟合得最好的一个控制组，记为M*（j），这一过程需要估计和比较2N-1-1种回归模型。因j=1，2，…，N-1，故重复这一过程，可挑选出N-1个备选的控制组M*（j），j=1，2，…，N-1。

第二步：利用AIC准则从M*（1），M*（2），…，M*（N-1）中再挑选一个AIC值最小的控制组作为最优控制组M*。

第三步：由控制组M*对应的估计模型（4） 进行样本外 （t=T1+1，…，T） 预测，作为舟山在政策发生后的“反事实”经济效率值，再由式（5）估计处理效应，作为分析依据。

3.2 实证分析及结果

由“反事实”分析方法及其步骤，利用实施政策前1995-2010年的数据，按照上述理论模型，并根据AIC准则，借助STATA软件选择最优拟合，最终得到由南京市、镇江市、温州市、蚌埠市、淮南市、淮北市、安庆市和滁州市组成的最优控制组，软件输出结果见表1，回归方程如下：

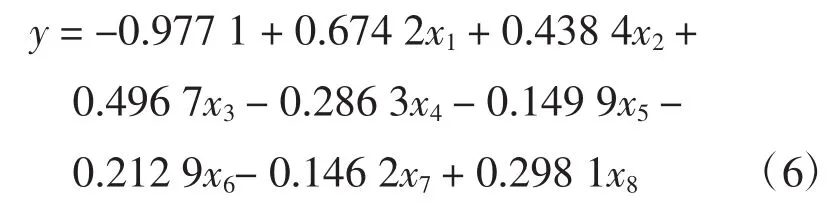
式（6） 的拟合优度较高，R2达0.998 2，并且方程总体显著性检验（F检验）与变量的显著性检验（t检验）都很好地通过。拟合值与实际值间的比较见图1，可以看出1995-2010年，选取的最优控制组确实能很好地拟合样本值。

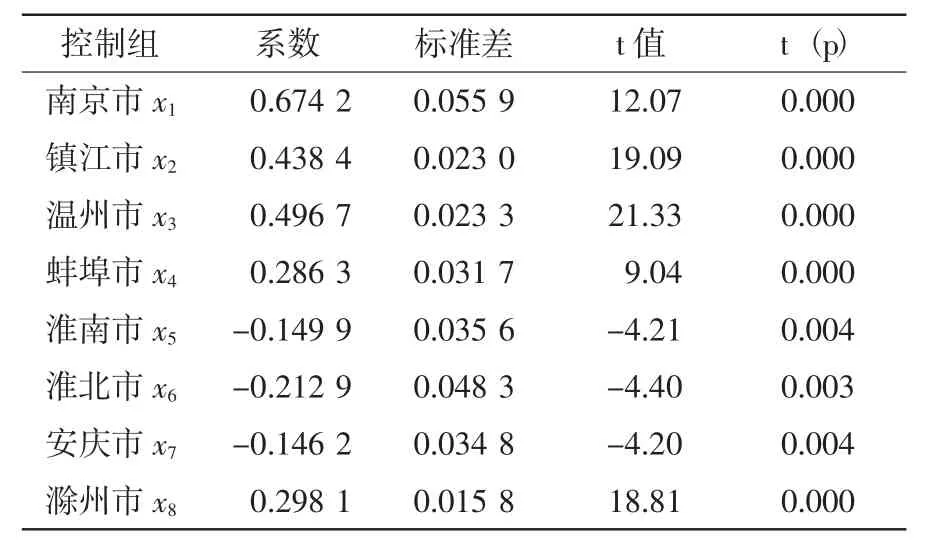
表2 1995-2010年舟山经济效率最优拟合系数及其检验值

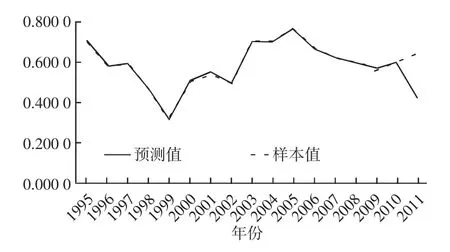
图1 最优控制组回归值与样本值的比较

利用拟合后的方程式（6） 进行样本外预测，得出若2011-2015年舟山未受到新区设立政策影响的“反事实”超效率值，并将实际值减去“反事实”值得出处理效应见表3。

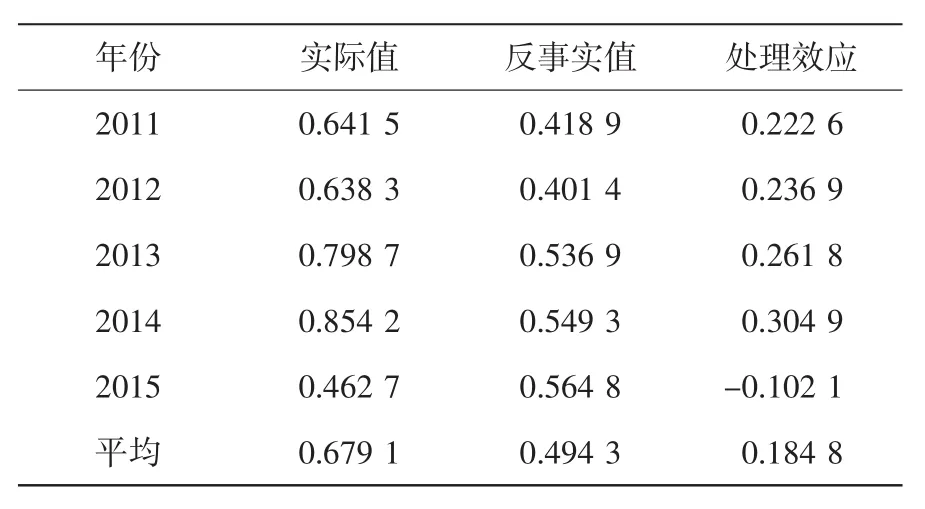
表3 舟山市经济超效率的实际值与反事实值

由表3可见，2011-2014年新区政策的处理效应均大于0，且2011-2014年处理效应由0.222 6逐年上涨到0.304 9，表明舟山市的经济效率在这些年相对其原有水平有明显提升，新区政策确实有效地促进了舟山地区的经济发展质量。但在2015年，处理效应小于0，显示政策的刺激作用几乎消失，表明新区政策对区域经济效率直接的刺激作用虽然有效，但持续时间有限，也就是说舟山市这几年由政策刺激获得的经济效率的提高不具有持续性。因此有必要及时改进与完善舟山经济发展的路径，通过自身的积极作为进一步发挥“政策红利”作用，促进地区经济持续的高质量发展。

3.3 理论模型的稳定性检验

上述研究结果显示，舟山群岛新区的成立促进了舟山地区经济效率的提高。但这种正效应是否具有偶然性，即是否是由于选择2010年这个时间点偶然引起的，需要进一步验证。设计检验方法为：选择舟山群岛新区成立之前的任一时间点代替上述模型中的2010年，然后进行类似反事实分析。若得到的拟合结果仍然与上述结果相同，即仍然在2011年开始处理效应为正，说明上述理论模型是稳定的，政策实施确实发挥了作用；反之，则表明该模型是不稳定的。

现假设舟山群岛新区成立提前两年，用以拟合的时间段为1995-2008年，“反事实”预测的时间段为2009-2015年。类似上文进行反事实分析后得到以南京、镇江、温州等10个城市为一组的最优控制组，拟合效果很好。拟合系数及其检验值见表4，回归方程为：

用式（7） 预测2009-2015年的“反事实”值，并将其与实际效率值（真实值）共同列于图2。可以看到，尽管用以拟合的数据只到2008年，但2009-2010年的拟合效果依然较好，且实际值还比“反事实”值略小。但从2011年起，“反事实”值开始处于实际值的下方，模型的处理效应结果与表3中基本一致，说明舟山群岛新区确实在其成立后促进了舟山的经济效率，本文的理论模型是稳定的。

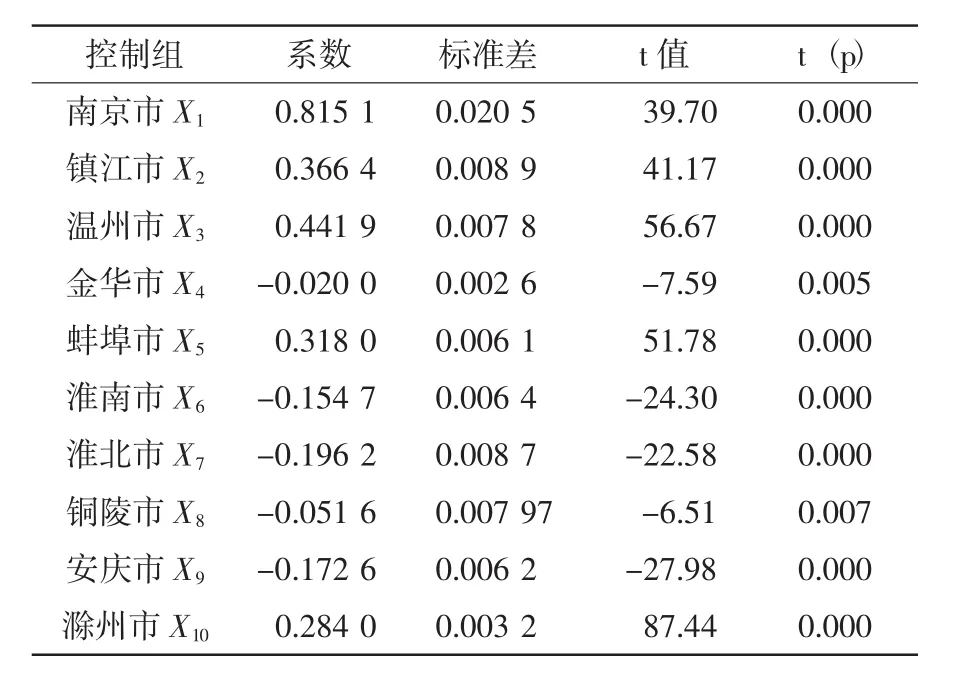
表4 1995-2008年舟山经济效率最优拟合系数及其检验值

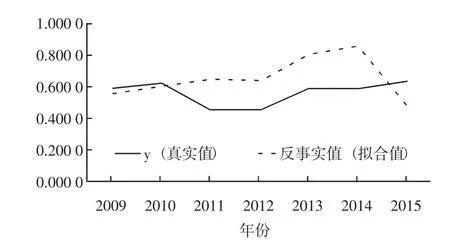
图2 舟山地区2009-2015年间实际值与“反事实”值比较（假设以2009年为政策实施节点）

4 结论及建议

利用1995-2015年的经济数据，测算了包含舟山市在内的共21个江浙皖地级市的经济效率，并以此构建“反事实”模型实证研究舟山群岛新区设立对舟山市经济效率的影响。研究显示，舟山群岛新区的设立显著促进了舟山地区经济效率的提高，表明国家级海洋新区建设有利于提高沿海地区的经济质量。但同时也发现，政策本身的刺激作用在时间上有限。到2015年，新区政策对舟山经济效率的影响几乎为零。

分析原因，2011年以来，舟山群岛新区建设全面拉开框架。舟山固定资产投资年均增长22%以上。波音项目、绿色石化基地、国家远洋渔业基地、宁波舟山港主通道、大陆引水二期、浙能六横电厂等重大项目分别开工建设或建成投用。因此这几年舟山经济效率的提高和其大规模的投资建设密不可分。但这种刺激作用持续性不强，舟山经济要长期高效的发展，还需要在投资拉动经济发展的基础上，乘势而上，充分利用好国家政策提供的机会，及时调整发展自己的特色产业，大力推进产业结构的优化升级。

表1的效率计算中也显示，虽然舟山群岛新区的设立一定时期内提升了舟山的经济效率，但在新区设立后最高的效率值也只有0.85，和其他20个城市比，仍未达到相对有效，说明舟山市经济建设中的资源配置和管理水平在这些城市中仍未达到相对最优，还有许多进一步改进与完善的空间。

综上所述，舟山群岛新区的设立，确实提高了该地区的经济效率，但舟山经济要持续的高质量发展，还有很多工作要做。舟山经济需要继续借助国家海洋新区政策的利好，努力提高经济建设管理水平，通过供给侧结构性改革，合理配置生产资源，进一步解放和发展生产力，做强、做精海洋特色产业，以促进舟山经济效率的不断提高。