基于博弈论组合赋权灰靶模型的煤矿安全综合评价*

毕 娟, 李希建

(1.贵州大学 矿业学院，贵州 贵阳 550025； 2.复杂地质矿山开采安全技术工程中心，贵州 贵阳 550025；3.贵州大学 瓦斯灾害防治与煤层气开发研究所，贵州 贵阳 550025)

0 引言

煤炭是我国的主要能源供给，在我国能源生产总量和消费总量中所占的比例均在2/3以上，占有非常重要的地位[1]。煤矿事故频发，重特大安全事故得不到有效控制，容易造成财产损失和人员伤亡。因此，加强煤矿安全监督与管理，将风险损失降低到最小，有效预防事故的发生，保证煤矿的生产安全是煤矿工作的重中之重。

目前对煤矿安全评价已取得多项研究成果。周忠科等[2]为了对安全隐患进行识别，针对煤矿安全生产特点构建了煤矿安全预警体系，利用BP神经网络算法对煤矿安全进行预警评估;汪刘凯等[3]通过因子分析与层次聚类分析，识别造成煤矿事故的主要风险因素，并利用软件计算出矿井安全事故风险因素的重要度;孟令玲等[4]利用层次分析法和模糊综合评价法建立了煤矿生产安全的评价体系，并将之实际应用在煤矿安全生产评价中;马金山、梁冰等[5-6]利用投影寻踪及智能加权灰靶决策对煤矿相对安全度进行分析，通过分析低维空间数据达到研究高维数据的目的;何叶荣等[7]通过问卷调查结合专家访谈获取煤矿安全管理风险因素，挖掘影响煤矿安全管理的关键点，利用Page Rank算法和结构方程模型对煤矿安全管理风险因素进行综合评价，并借助软件工具对模型进行验证。应用这些方法进行评价，存在一定的主观性和模糊性，且计算过程复杂，准确度不够。而评价煤矿安全涉及到很多定义界限不明确、人为判断不精准的情况，很难精确预测和描述。

鉴于此，在以上研究成果的基础上，建立博弈论组合赋权耦合灰靶决策模型，可以很好地解决样本数据少、指标多和信息模糊的不确定性问题[8]。首先，以事故致因理论为基础，确定影响煤矿安全的主要因素。其次，运用层次分析法、熵权法和神经网络算法单独计算出各个指标的权重，根据最优线性组合确定博弈论组合赋权。最后，利用博弈论组合赋权耦合灰靶决策模型计算矿井的靶心距，对煤矿的安全性进行排序，确定煤矿的安全等级。

1 博弈论确定评价指标权重

1.1 单一指标权重确定

评价指标的权重由决策者综合考虑各种主客观因素得到，反映了相应指标对评价结果的重要程度。单一权重确定法容易忽略每个基本权重间的偏差，采用博弈论组合赋权，将多种权重确定法组合优化，将可能的权重与每个权重间的各自偏差极小化，得出最优指标权重。

熵权法是通过计算指标的变异程度来反应指标熵值的大小。样本中的某一评价指标变异程度越大，所含信息量就越复杂，权重亦越大，对煤矿安全等级的影响程度越大。其具体计算步骤见文献[10]，所确定的指标权重记为W(2)=(W21,W22,…,W2m)。

神经网络算法是通过对样本的反复学习来分析结果，需要大量的数据样本，样本数据不足时精度较低。采用神经网络算法确定指标权重，具体步骤见文献[11]，所确定的指标权重记为W(3)=(W31,W32,…,W3m)。

1.2 博弈论组合赋权

博弈论组合赋权法就是将不同方法确定的权重值进行组合优化，确定指标权重的最优结果[12]。假设总共运用p种方法对每个指标进行赋权，从而可以确定p个权重向量。

W(q)=[wq1,wq2,…,wqm],(q=1,2,…,p)

(1)

式中：W(q)为第q种方法确定的权重向量。

则此p个权重向量的线性组合为：

(2)

式中：αq为线性组合系数，αq>0；W为所有的权重向量集。

根据博弈集结模型的思想，对不同权重进行最佳优化组合，寻求不同权重间的一致和妥协，即以离差极小化为目标，对P个权重向量组合系数αq进行优化，得到W中最满意的权重。

好莱坞枪战片中，镜头：攻坚克难时，通常由A队（Alfa阿尔法队）担当主攻，由B队（Bravo勇敢者队）协助、掩护进攻，或PLAN B方案。最终目的是解决问题。图书馆学研究作为社会科学的一支，既要关注行业问题，深入开展内涵式研究（A面研究）；也要关注社会问题，以图书馆学的学科理论与方法，共同参与、解决日益复杂的社会现实问题，彰显学科影响力（B面研究）。两者相辅相成，缺一不可；在以问题为导向的现代社会科学研究范式中，直面学科发展与突破，B面研究将更为重要。当然，我们也要始终牢记图书馆学学科独有的理论与方法。

(3)

式中：W(o)为第o种方法确定的权重向量。

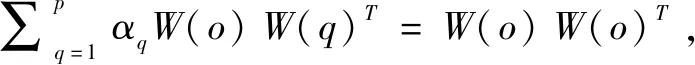
(4)

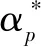
(5)

2 博弈论组合赋权的灰靶模型

2.1 灰靶决策基本原理

灰靶决策是解决多指标决策问题的一种方法[14]，为减少决策中出现的失误，保证决策过程的客观公正，越来越多的问题都采用群决策方式解决。多指标群决策灰靶模型在没有标准模型的条件下，在一组序列中，找出最靠近临界值的数据构建标准模型，然后将待评模型与标准模型进行比较，以此识别待测模型接近靶心的程度，最后计算出靶心距，从而确定煤矿安全评价等级，能够有效避免实际偏差，很好地解决不确定性多指标决策中存在的问题。

2.2 灰靶决策模型评价

设煤矿安全多指标决策问题中，决策方案集为A={A1,A2,…,An}，其中Ai表示第i个决策方案；指标集为m个评价指标组成的集合，记为C={C1,C2,…,Cm}，其中Cj表示第j个评价指标；指标的权重值为W={W1,W2,…,Wm}。

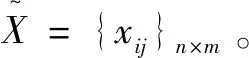
效益型指标：

(6)

成本型指标：

(7)

2.3 指标偏离靶心度

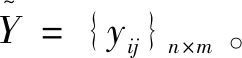
yij=[xijwj]

(8)

对第j列，将max{x1j,x2j,…,xnj}所在行列位置记为+ij，该位置对应的值记为+yj。+yj为灰靶决策的最优效果向量，称+yj为决策指标的正靶心。+y={+y1,+y2,…,+ym}。

对第j列，将min{x1j,x2j,…,xnj}所在行列位置记为-ij，该位置对应的属性值记为-yj。-yj为灰靶决策的最劣效果向量，称-yj为决策指标的负靶心。-y={-y1,-y2,…,-ym}。

决策方案Ai的加权群正靶心距见式(9)。

(9)

决策方案Ai的加权群负靶心距见式(10)。

(10)

加权群正靶心距越小，对应的方案越优，加权群负靶心距越大，对应的方案越优。综合考虑两者的大小，确定每个方案的群偏离靶心度Si，利用Si的大小对各方案进行排序，Si最大值对应的方案即为最优方案。

(11)

3 实例分析

以义马煤业集团5组矿井资料为样本数据[16]，采用博弈论组合赋权确定指标的权重，利用多属性灰靶决策模型对煤矿安全现状进行综合评价。根据煤矿安全所涉及的范围与内容，基于事故致因理论和可靠性原理，从“人-机-环-管理”4个方面，确定煤矿安全的评价指标，用Cm表示。义马煤业集团5组矿井原始数据及评价指标见表1。

3.1 确定煤矿安全指标权重

通过层次分析法、熵权法和神经网络算法确定每个指标的权系数，再根据博弈论组合赋权的思想确定综合权重。运用式(2)～(4)可确定3个权重向量的最优线性组合系数(α1，α2，α3)，经过归一化处理后，确定为(0.063，0.494，0.443)，根据式(5)计算得出最优组合博弈论权重W。层次分析法、熵权法、神经网络法和博弈论组合赋权法确定的权重向量见表2。

3.2 确定综合靶心距

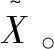
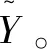
计算矿井的偏离靶心度，首先确定每个评价指标的正靶心和负靶心。根据max{x1j,x2j,…,xnj}原则确定指标正靶心，根据min{x1j,x2j,…,xnj}原则确定指标负靶心。利用式(9)～(10)计算得出5组矿井的正靶心距和负靶心距，结果见表3。

根据式(11)计算得出博弈论组合赋权耦合灰靶决策模型的偏离靶心度。同时，还分别采用层次分析法耦合灰靶决策模型、熵权灰靶决策模型和神经网络算法耦合灰靶决策模型对5组矿井的煤矿安全现状进行综合评价，计算得出不同模型的偏离靶心度Si1，Si2，Si3，Si4。4种灰靶决策模型的偏离靶心度结果见表4，为方便对比，将4种灰靶决策模型的偏离靶心度结果绘制成折线图，见图1。

3.3 结果分析

5组煤矿的安全等级排序为：矿井4>矿井5>矿井1>矿井2>矿井3，与实际情况相符，说明该模型对煤矿安全现状的评价是合理的。

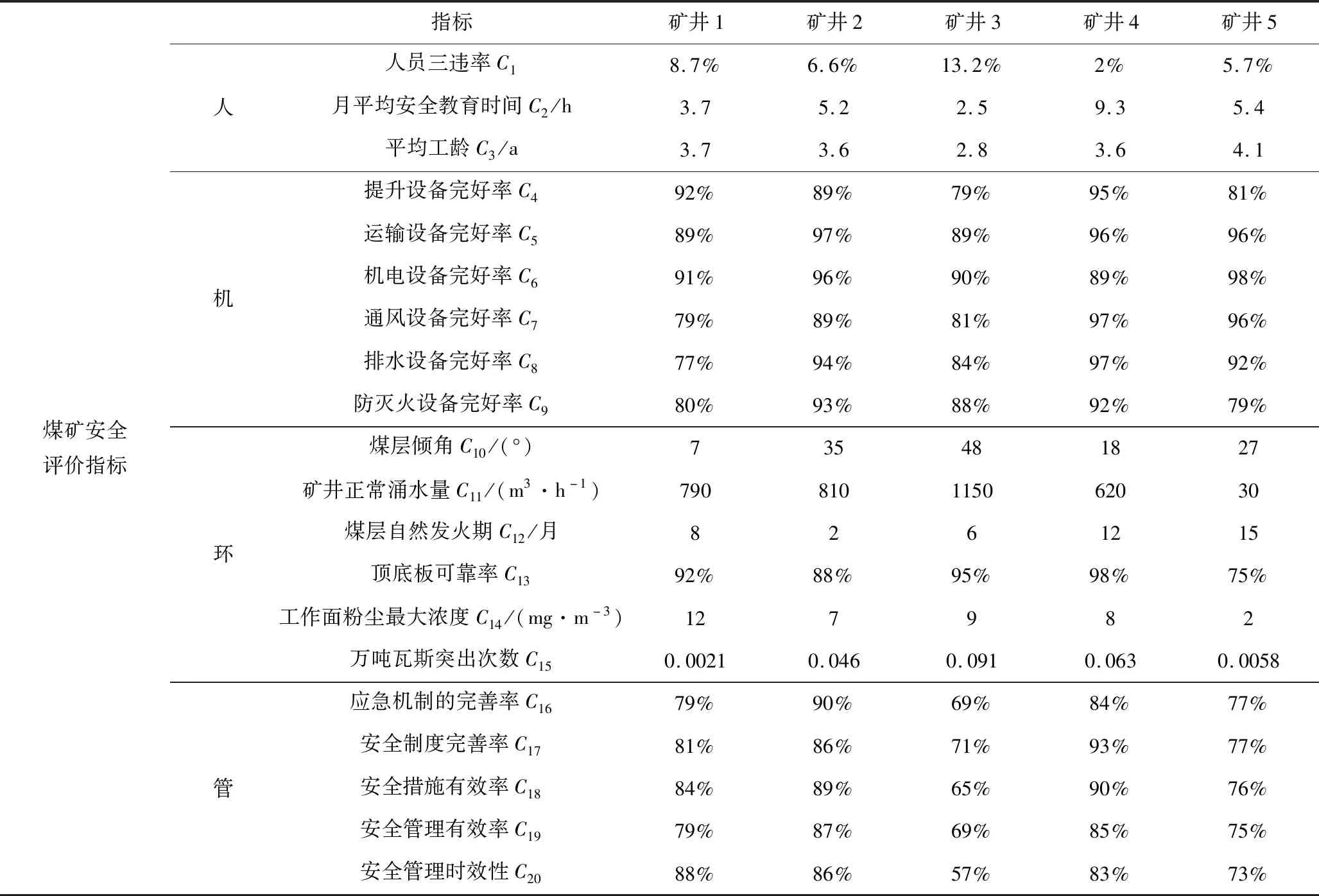
表1 煤矿安全评价指标体系及矿井数据Table 1 Evaluation index system of coal mine safety and data of mines

表2 评价指标的权重向量Table 2 Weight vectors of evaluation indexes

表2(续)

表3 矿井正靶心距和负靶心距Table 3 Positive and negative target distance of mines

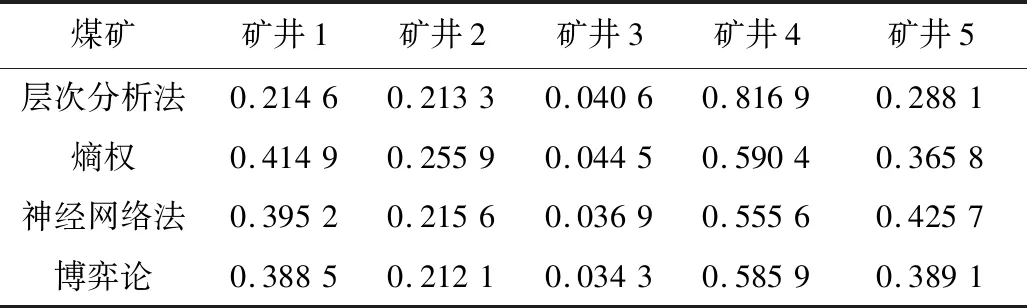
表4 4种灰靶决策模型的偏离靶心度Table 4 Degrees of deviation target of four grey target decision-making models

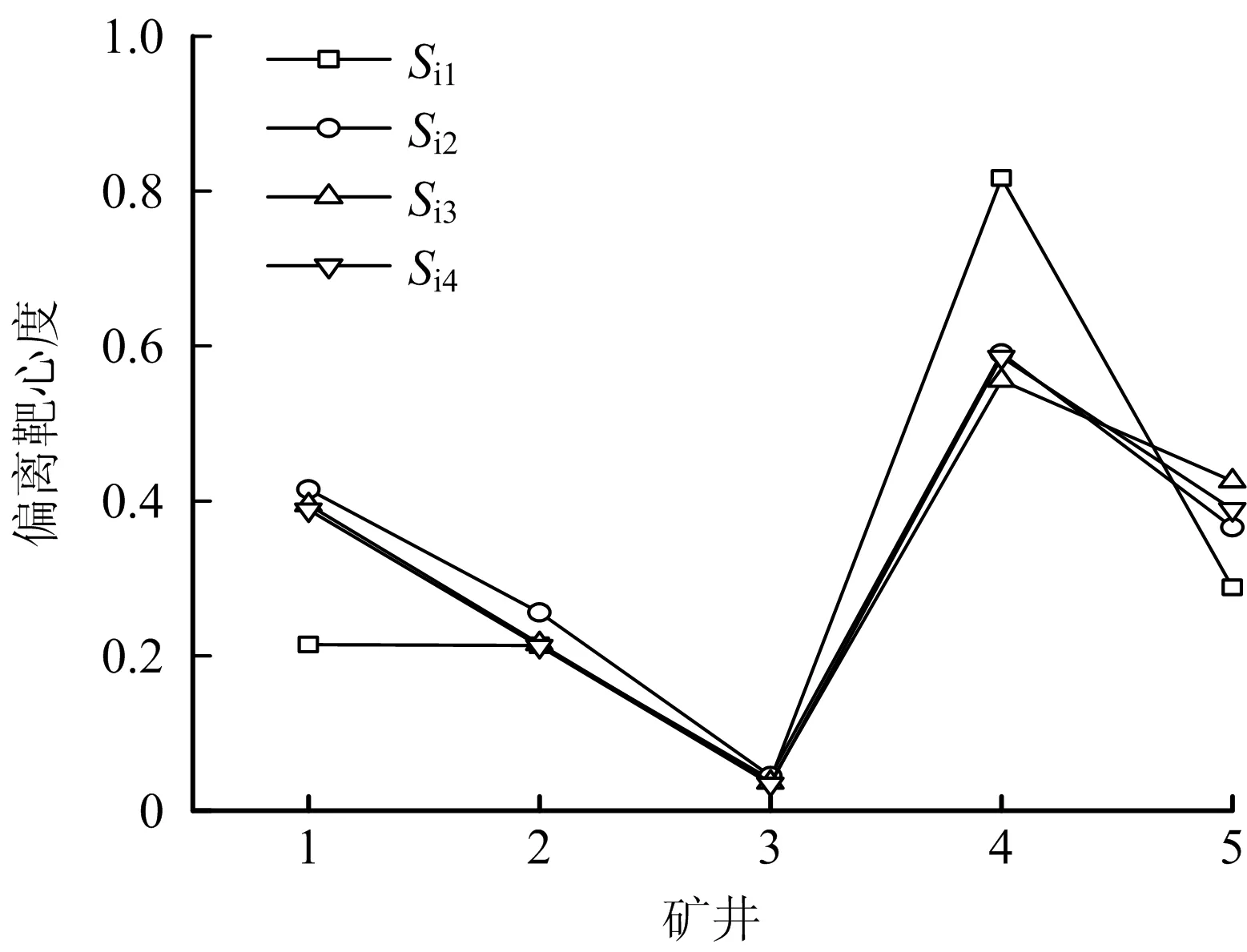
图1 4种灰靶决策模型的偏离靶心度折线对比Fig.1 Comparison of broken lines for degrees of deviation target of four grey target decision-making models

博弈论组合赋权的灰靶决策模型与层次分析法耦合灰靶决策模型、神经网络算法耦合灰靶决策模型的评价结果排序一致；而熵权灰靶决策模型矿井1的安全程度大于矿井5，其余矿井安全现状排序相同。博弈论组合赋权的灰靶决策模型与熵权灰靶决策模型、神经网络算法耦合灰靶决策模型的偏离靶心程度结果相近，而层次分析法耦合灰靶决策模型相较其他3种方法差距较大，存在一定误差。层次分析法由决策者打分决定，单一决策者打分易出现误差，多个决策者打分时，不同决策者偏好的指标不同，且决策者之间也存在优劣问题，对权重的计算造成很大误差。适当考虑决策者的权重问题、决策者偏好信息的集结和决策群体偏好的确定有利于减少层次分析法带来的人为误差。神经网络算法耦合灰靶决策模型与博弈论组合赋权的灰靶决策模型偏离靶心度结果相近，但神经网络算法确定权重的计算比较复杂，需要大量原始数据的支撑，样本数量过少可能造成精度不够。因此，综合考虑博弈论组合赋权的灰靶决策模型结果合理可靠，且计算简便精准，可为管理煤矿日常安全提供一定的理论依据。

4 结论

1)运用层次分析法、熵权法和神经网络算法单独确定各个指标的权重，计算出最优线性组合系数为0.063，0.494，0.443，最后根据归一化后的系数确定博弈论组合赋权。

2)考虑到评价煤矿安全指标的属性不同，灰靶决策方法将指标分为“成本型”和“效益型”分别计算，根据靶心度的大小确定煤矿的安全程度。

3)通过样本实例检验，基于博弈论组合赋权的灰靶决策模型适用于评价煤矿安全情况，根据结果分析可实现对薄弱环节的及时排查，为决策者评价煤矿安全性提供一种理论依据。