双风机并联机站局阻特性研究*

王文才，赵晓坤，梁素钰

(内蒙古科技大学 矿业研究院，内蒙古，包头 014010)

0 引言

机站通风作为矿井局部风量调节方法和多级机站通风系统基本单元，具有风量调节灵活、易控制、低能耗等诸多优点[1-3]，在较多矿山推广应用中均取得了显著的社会效益和经济效益[4]。机站局部阻力占风机全压比例较大，尤其多风机并联时机站风流结构复杂，通风设计参数依靠经验取值，常导致机站设计数据和实际运行参数不符，造成通风能耗损失。

机站通风是提高矿井通风系统各项指标有效的技术手段[5]，相关学者针对机站局部阻力组成及其局阻特性以及测试方法等方面进行了诸多研究。文献[6]用N-S方程揭示了机站局阻的实质，阻力损失主要存在于进口加速缩小、出口突然扩大、进口分流和出口多股风流汇流等，并提出采用叉管结构减少多股气流的相互冲击；程厉生[7]用功率消耗的概念推导了机站通风的总能耗，提出了机站局部阻力及其系数测定的理论依据，给出了装有扩散器、集流器的多风机并联机站局阻及其系数的常用计算表达式，同时建立对方形断面的机站通风模型，并对不同风机并联台数的通风机站相关参数进行了测试，得出机站局阻系数计算的综合校正系数Kc值与风机并联台数呈正相关；李雨林等[8]在上述测试的基础上对并联4台风机、不同外阻情况下对机站局阻系数进行测定，得出综合校正系数Kc随风机台数的增加而增加，说明风机并联数越多，进口分流与出口汇流造成的机站局阻损失越大。目前针对流体分流与汇流方面的研究主要集中于定性分析局部阻力产生机理及流场特性[9-11]，文献[12]采用数值模拟与现场实测结合的方法，对巷道交叉对通风局部阻力的影响进行分析研究，得出设计巷道时应尽量减少分流与钝角汇流；文献[13-14]通过大涡数值模拟对流体交汇处流场进行了研究，得出了各因素对局部阻力、流体特性及其空间分布的影响机理，定量分析了断面不均匀系数的分布规律，为研究交汇处流体特性变化的本质提供参考。相关文献中的研究成果对双风机并联机站的局部阻力损失的影响因素考虑的不够全面，忽略了测点间的沿程阻力损失，以及对机站入口分流、出口汇流导致断面速度分布不均匀引起的附加能量损失研究较少，且缺乏完善并试验验证的机站通风局部阻力的普遍表达式。本文通过理论分析、相似实验，佐以数值模拟的方法，在分析双风机机站风流特性以及阻力损失机理的基础上，总结适用于机站局部阻力系数计算的普遍表达式，以期为井下通风机站设计参数选取提供参考。

1 双风机并联机站通风理论模型

双风机并联机站风流流动模型如图1所示，1-1，2-2断面假定为机站入口和出口侧风流速度、风压均匀断面，2-2，3-3断面间只存在沿程损失。

图1 双风机并联机站风流示意Fig.1 Schematic diagram of air flow in double-fan parallel station

多风机机站结构中，相同特性风机在断面1-1，2-2断面间产生的全压差一致，且各风机风量相同、全压相同，此时全流量能量方程为：

(1)

定义机站有效风压Hs为：

(2)

能量方程改写为：

Hf=hj+Hs

(3)

(4)

式中：Hs为机站风压(或机站外阻)，Pa；P1，P2分别为1-1，2-2断面的平均静压，Pa；v1，v2分别为1-1，2-2断面的平均风速，m/s；hj为机站局部阻力，Pa；ξj为机站局阻系数；hf为测试断面间的摩擦阻力，Pa；Hf为风机全压，Pa；δ为机站局阻与风机全压的百分比，表示局阻大小。上述公式给出了机站局阻及其系数测定的理论依据，以及局阻大小判定标准。

井下巷道风流多为紊流状态，忽略进口分流、出口汇流风流间相互掺混引起的附加摩擦阻力损失，1-1，2-2断面间的沿程损失为：

(5)

式中：hf2-3为断面2-2，3-3间沿程损失，Pa。

分析上述公式得出，风机全压一部分克服机站负担区域的通风阻力，另一部分消耗于机站局部阻力。矿井通风的目的是以最小的能耗获得最佳的通风效果，当巷道断面与需风量一定时，尽量减小机站局部系数是机站通风节能降耗的主要目的，ξj的一般表达式为：

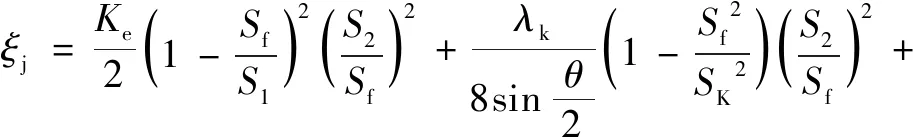
(6)

式中：Ke为机站进口条件系数，与机站风机入风口结构相关，一般为实验测定；S1为机站入风侧巷道断面，m2；S2为机站出口巷道断面积，m2；Sf为机站风机入口断面积，m2；λk为扩散器内部沿程摩阻系数；θ为扩散器的扩张角，(°)；SK为扩散器出口断面积，m2。

多风机并联时引入综合校正系数Kc，则校正后的机站局阻系数ξ为：

ξ=Kc·ξj

(7)

综合校正系数Kc没有明确的理论公式计算，只能由实验求得，本研究的目的在于确定Kc变化规律及取值标准。

2 相似实验及数值模拟验证

2.1 实验模型及测量系统

根据矿井实际生产设计模型率为1∶4的相似实验模型，制作表面粗糙的木制巷道长30 m，断面为1.2 m×0.8 m的相似模型(壁面粗糙高度ks约为0.01 m，此模型的壁面摩擦与实际巷道较为接近)。实际巷道风速较大，雷诺数Re>5×105，所以主要考虑在几何相似和边界条件相似的前提下[15]，选用2台低噪声轴流风机SFG-2.5-2#，使得模型内的空气流动发展成完全紊流即可。风机入口安装曲率半径为0.08 m的集流器，出口安装长度为0.5 m、扩张角16°的扩散器，选用JTY-4通风多参数测定仪测量数据，风机以巷道中轴线对称布置，巷道出口处加装挡板用以改变巷道风阻实现多工况实验。引入参数σ表示风机工况参数的无因次量，代表测试点时风机的工况位置，公式为：

(8)

式中：Ht，Hm分别为风机在实际工况点和高效点工作时的全压，Pa；Qt，Qm分别为风机在高效点和实际工况点工作时的风量，m3/s。当σ=1时，说明风机在特性曲线的高效点工作；当σ>1时，说明风机实际工况点在高效点左侧；当σ<1时，说明风机实际工况点在高效点右侧，同时反映巷道外阻的大小。

实验模型如图2所示。取风机入口所在断面中心点为原点，x轴正方向为风流出口方向；y轴垂直指向巷宽一侧；z轴垂直指向巷高一侧。x正方向布置12个测面，其中10个断面距扩散器出口1d～5d(d为模型巷道断面当量直径，m)，间隔0.5d，剩余2个断面为8d，10d；x负方向布置6个测面，距集流器入口-0.5d～-3d，间隔0.5d。由于实验模型为对称结构，在测面布置测线及测点时，选取y>0，z>0区间进行布置，间隔0.1 m，具体如图3所示。

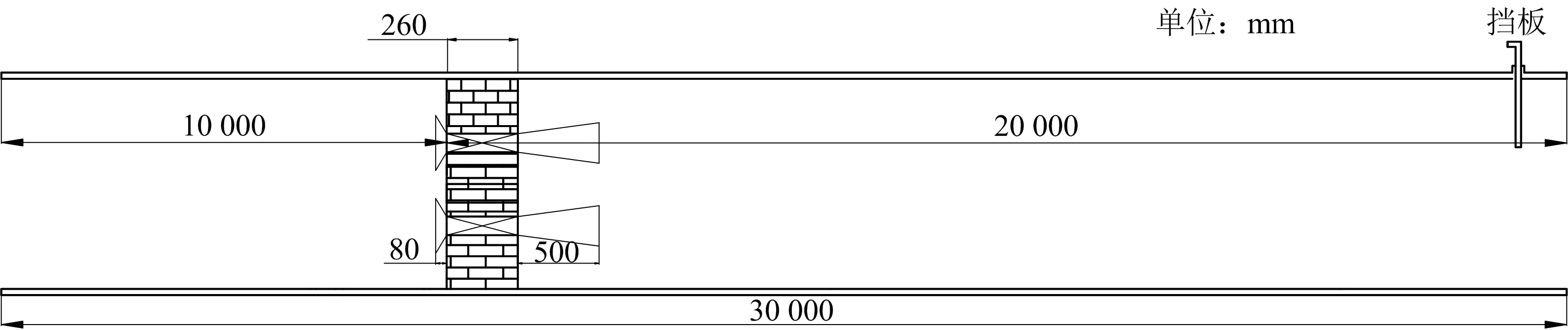
图2 双风机并联通风机站结构Fig.2 Structure of double-fan parallel ventialtion station

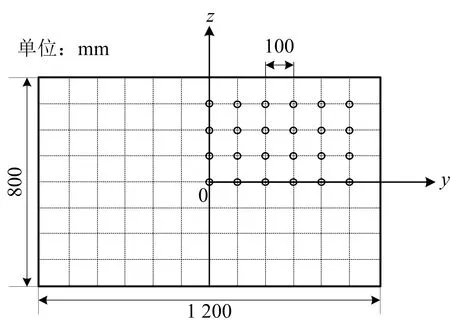
图3 断面测点布置Fig.3 Layout of sectional measuring points

2.2 数值模拟

按照模型试验原型进行数值模拟。机站通风流场复杂，为降低数值模拟难度，假设巷道内流体为恒温、绝热、不可压缩的定常紊流状态；由于模型内存在风机，采用非结构性网格对风机周围计算区域进行局部加密；计算采用标准k-ε紊流模型与流体力学方程进行数值模拟[15]，速度压力耦合采用Simplec格式，离散项采用一阶迎风格式；边界条件设定见表1。

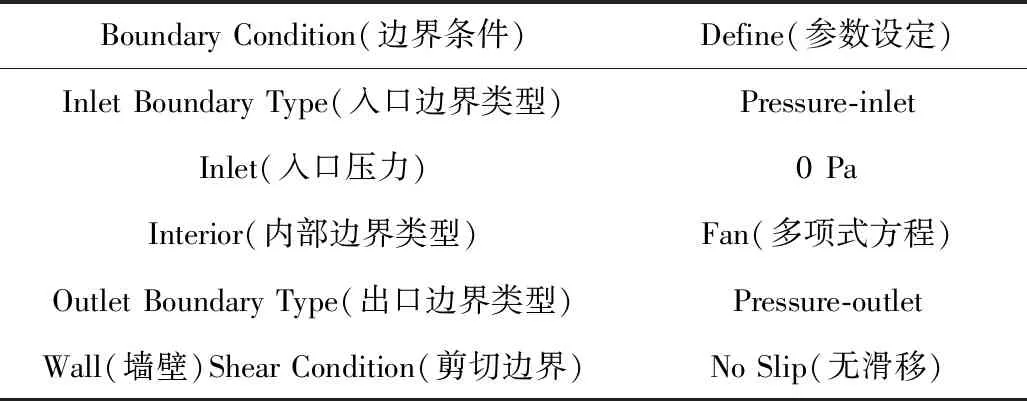
表1 边界条件设定Table 1 Setting of boundary conditions

2.3 模型验证结果

选取坐标z=0处的实验数据验证数值模拟结果，选取挡板3个不同位置作为验证工况。限于篇幅，仅给出机站入风侧、回风侧各2个断面(-2d，-0.5d，1d，3d)的速度对比结果，如图4所示。结果表明数值模拟与实验测量数值基本吻合且变化趋势一致，部分测点数据数值不完全相同，可能是由于实验环境差异、测量误差和网格精度的因素导致，总体误差在可接受范围内。模拟数据与实验结果较为吻合，验证了数值模拟中网格划分方法、边界条件设定、求解模型选取以及各求解参数设定合理，数值模拟结果具有较高精度，可用于通风机站局阻研究。

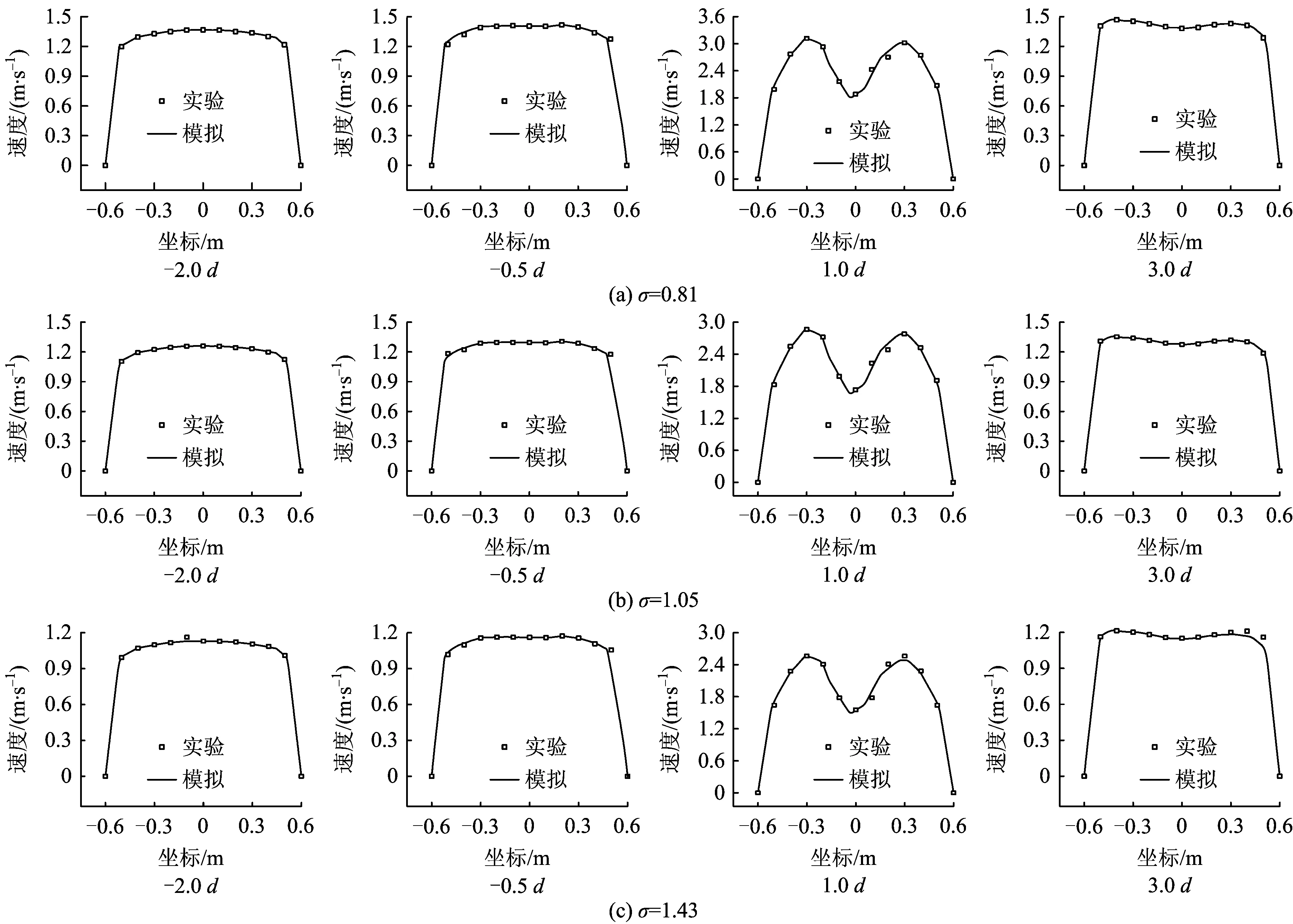
图4 数值模拟与实验值结果对比Fig.4 Comparison of numerical simulation results and experimental results

3 数值模拟结果分析

3.1 入口分流、出口汇流的不均匀性

巷道风流在机站入口、出口的分流、汇流过程中产生较大的能量损失，风流速度分布在调整过程中，由于主流区的速度梯度较大以及两股风流之间相互掺混引起内摩擦力增加，导致风流能量除进口缩小、出口扩大之外的附加能量损失。引入测量断面测点流速方差s2来描述机站入口、出口流速分布不均匀性[16]，其表达式为：

(9)

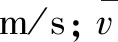
图5为不同工况条件下机站入口、出口断面s2沿流速方向的分布曲线。由图5(a)得出在距离集流器一定距离内(0～1d)，沿程变化较为迅速，之前一段距离内(1d～2d)沿程变化较为缓慢，距离集流器入口大于2d前，s2基本保持不变且量值较小，距离集流器越近，s2越大，测试断面可选择在距集流器入口大于2d的范围内；变工况条件下机站入口断面s2沿程变化趋势整体相似，工况越大，不均匀程度越小，说明风机风速越小，风机间风流相互影响作用减弱，机站入口分流形成的附加阻力损失较小。由图5(b)得出，风流从扩散器出口流出，风机间相互影响剧烈，s2较大，在距离扩散器出口一定距离内(0～2.5d)，沿程变化较为迅速，之后一段距离内(2.5d～5d)沿程变化较为缓慢，随后s2基本保持不变；变工况条件下机站出口断面s2沿程变化趋势整体相似，距离扩散器出口较近范围内，工况越大，s2越小，说明风机风速越小，风机间风流相互影响作用越不明显，机站出口汇流形成的附加阻力损失较小，测试断面可选择在距扩散器出口大于5d的范围内。

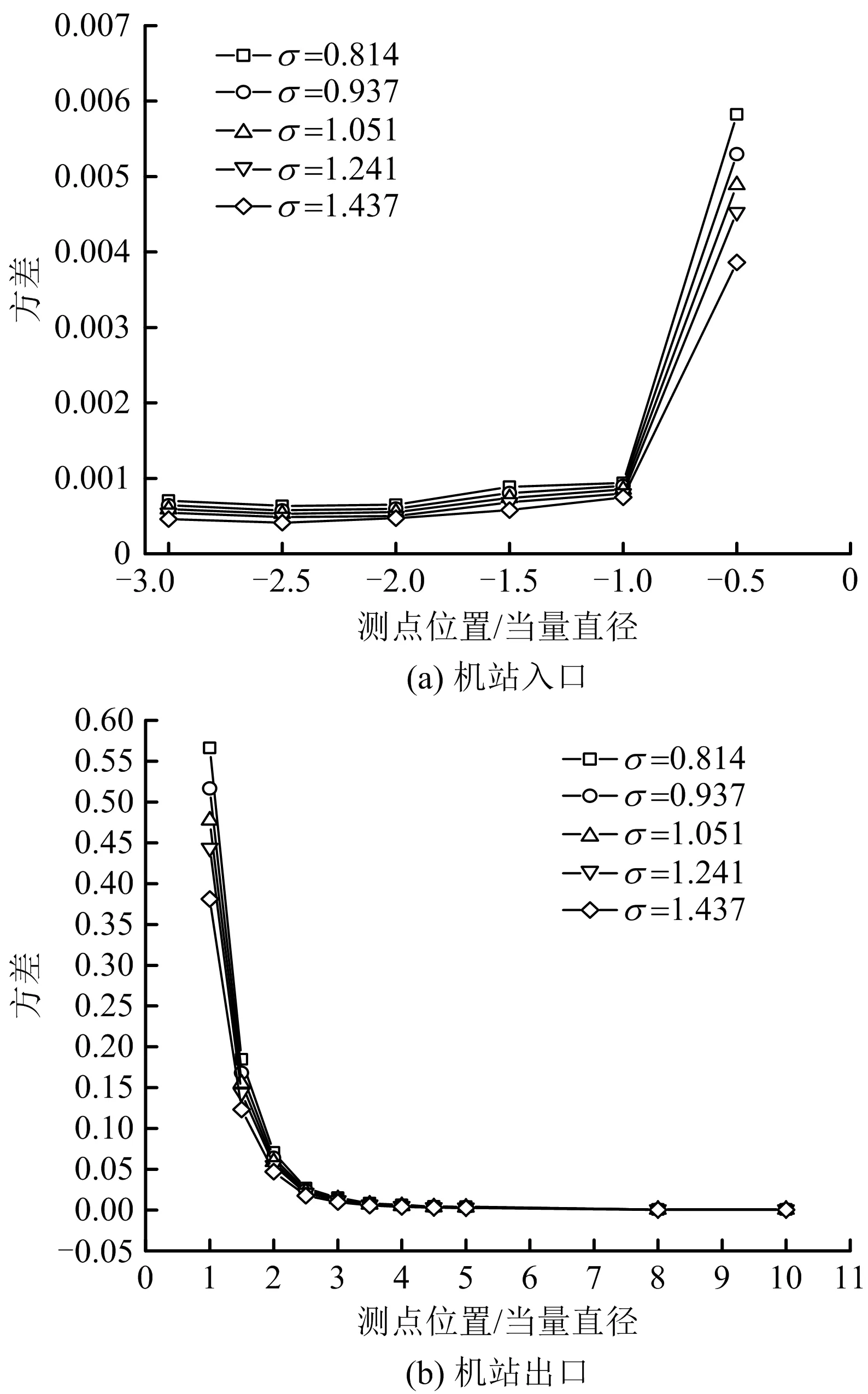
图5 不同工况下机站入口、出口的不均匀系数Fig.5 Unevenness coefficients of inlet and outlet of fan station under different working conditions

综合比较机站入口、出口断面不均匀性发现，在所测试区间内，入口不均匀性峰值大小较出口而言基本可以忽略，主要由于机站出口风流动量和能量的剧烈交换所致，上述结果印证了文献[8]中对装有集流器的机站，出口段是机站降阻主要对象的论述。

3.2 综合影响系数Kc的确定

通风机站局部阻力的判定标准为风机定工况下的风压损失率，在设计低阻力机站结构以及风机选型时，合理确定综合影响系数Kc成为关键。为研究巷道断面积相等、不同宽高比条件下的Kc的变化规律，分别对断面为1 m×0.96 m，1.3 m×0.74 m，1.5 m×0.64 m，1.6 m×0.6 m，宽高比A分别为1.04∶1，1.76∶1，2.34∶1，2.67∶1的不同模型做变工况数值模拟计算，此时测量断面选择为L1=3d，L2=10d，L3=5d。机站风机间距对局阻系数的测试结果影响较小[7]，实验仅以断面形状参数A整理分析计算结果，如图6所示。

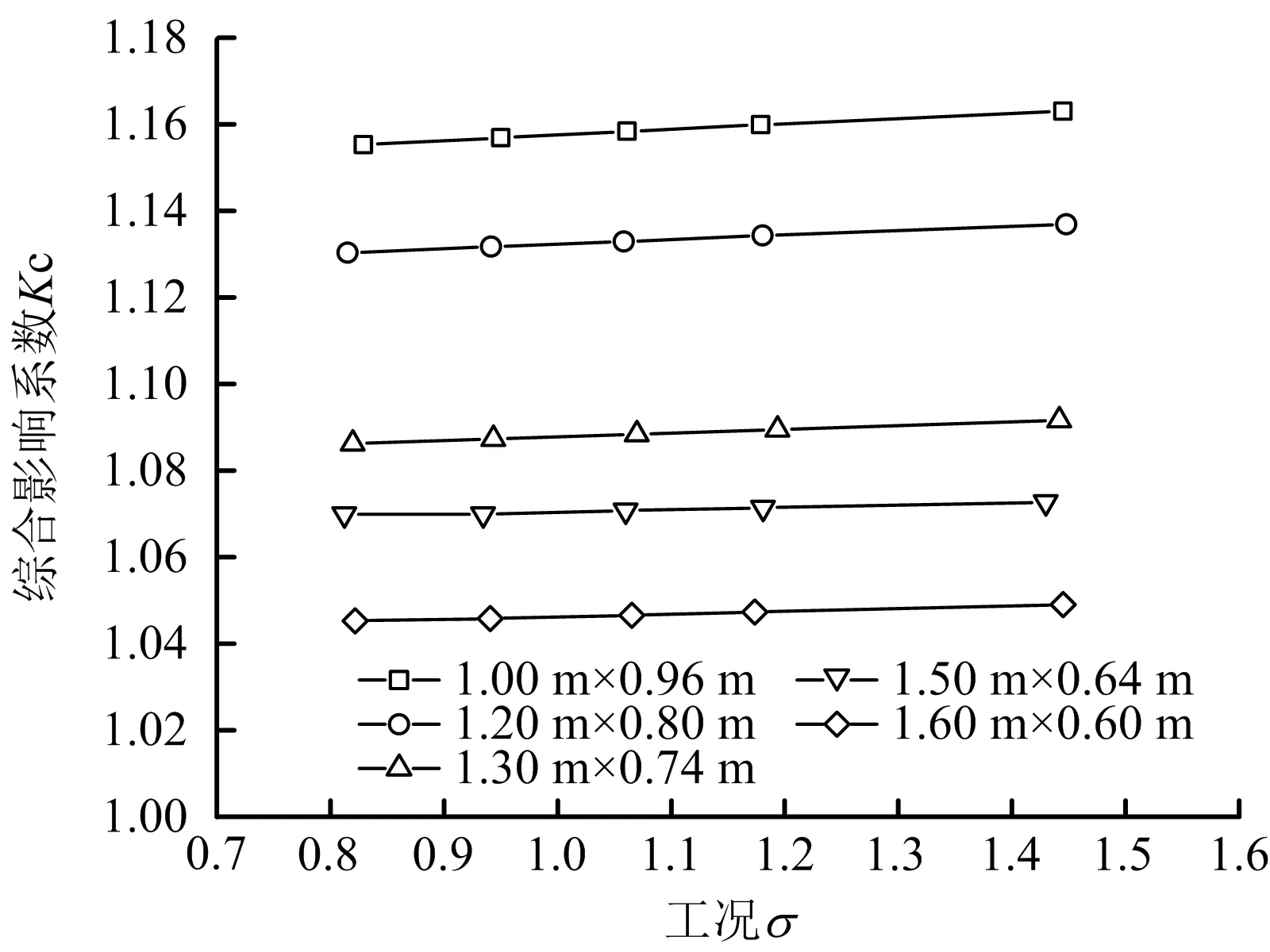
图6 不同模型变工况Kc-σ关系Fig.6 Relationship of Kc-σ under variable working conditions in different models

由图6可知：各模型的Kc随工况的增加而增加，机站的局阻系数随之增大，说明ξ并非常数，此时机站风压损失率随工况增大而减小，与近机站入口、出口断面速度分布不均匀性呈现正相关；各模型的Kc与σ均呈现较好的线性关系，建立回归方程Kc=a+bσ，相关参数见表2，数据拟合相关性较好。

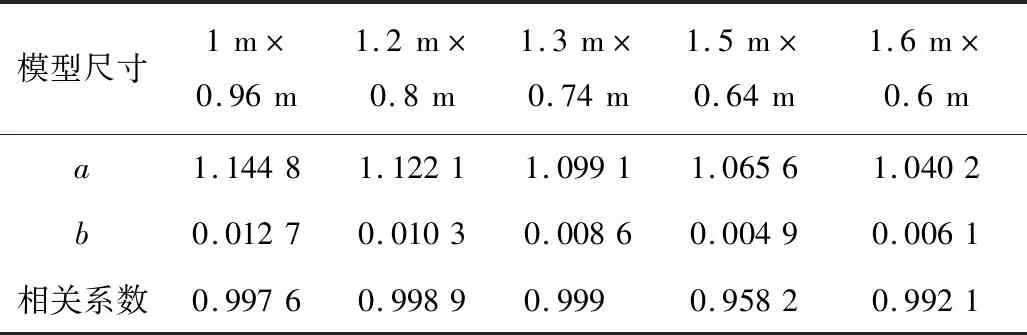
表2 回归方程相关参数Table 2 Related parameters of regression equation

计算整理各模型高效工况点(σ=1)时Kc得图7。由图可知：随着宽高比A值的增大Kc逐渐减小，呈现较好的线性关系，针对数据进行对数函数拟合，得Kc=1.231-0.069A，相关性系数为0.995。说明风机工况相同、定断面积条件下，宽高比值越大，机站入口分流、出口汇流造成的附加损失越小，机站有效风压越大，有利于克服巷道较大的通风阻力，实现了机站通风的低阻、高效，节省电能的消耗。

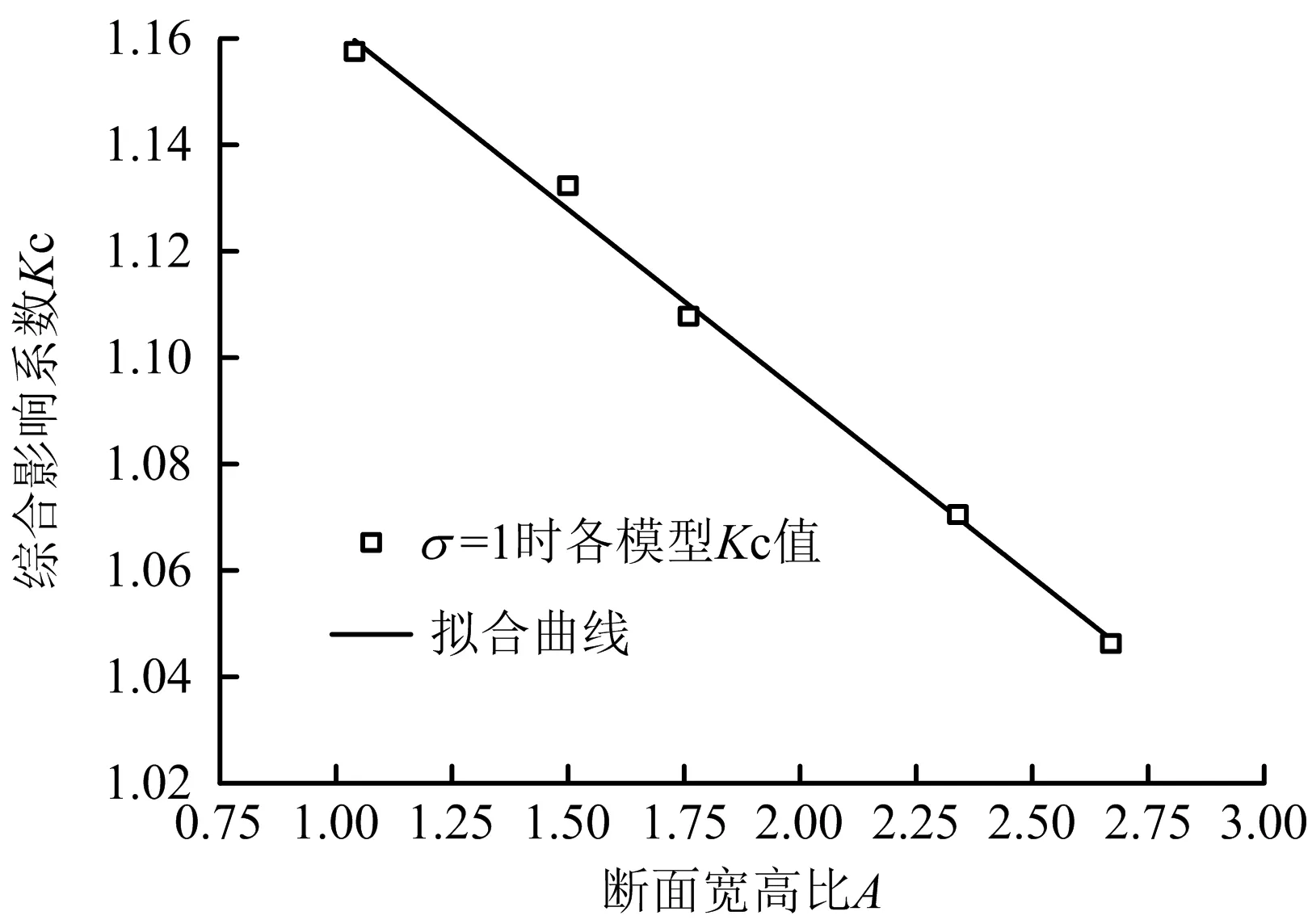
图7 不同模型高效工况Kc-A关系Fig.7 Relationship of Kc-A under high-efficiency working condition in different models

4 结论

1)机站通风测试断面应选择在集流器前2d、扩散器后5d的范围内，以保证测试数据准确、可靠。

2)机站局阻计算时应排除沿程阻力的影响，避免由于沿程损失较大而导致机站局阻计算值偏离实际，从理论上完善了机站局阻及其系数计算公式。

3)数值模拟得到了与相似实验吻合度较高的计算结果，可作为研究机站局部阻力变化规律以及结构设计的有效方法，模拟结果符合设计要求。

4)风机间相互影响系数Kc随风机工况σ增大而增大、随断面宽高比A增大而减小，并具有较好的线性关系，同时总结了Kc-σ，Kc-A的关系方程，为机站通风设计计算及风机选型标准和规范等提供方法参考。