基于三角模糊语言变量的供应商选择问题研究
2019-08-13谢志烈刘曦泽顾巧祥
谢志烈,刘曦泽,顾巧祥
(中国计量大学 质量与安全工程学院,浙江 杭州 310018)
供应商选择是企业最重要的组织决策之一,其结果对产品质量以及组织和供应链的绩效有重大影响[1-3]。供应商选择是一个典型的多属性决策问题,目前运用的方法主要有简单线性加权法、层次分析法、灰色关联法、TOPSIS方法和模糊综合评价法等[4]。在多属性决策过程中,由于客观事物的不确定性和复杂性,以及决策者思维的模糊性,从而导致决策信息往往以语言变量或称不确定语言来表示。因此,基于不确定语言信息或语言变量的多属性决策问题已成为多属性决策领域的一个研究热点[5-7]。李香花等[8]通过采用三角模糊语言变量,将决策者的评价意见转换成三角模糊数,结合层次分析法对模糊决策判断矩阵进行模糊变换和向量计算,计算出备选模式的综合权重,并据以制定决策方案;梁雪春等[9]针对梯形模糊语言变量,通过对两个梯形模糊语言变量对比的可能度公式进行定义,并进一步研究其基本性质,提出了基于梯形模糊语言变量的可能度公式的方案排序方法;刘超等[10]提出了区间对偶犹豫不确定语言集的概念,研究了区间对偶犹豫不确定语言变量相关的基本理论与方法,并针对属性值为区间对偶犹豫不确定语言信息的关联多属性决策问题,提出了相应的决策方法。
综上,本文提出了三角模糊语言变量的期望值公式,在此基础上利用信息熵法确定了属性权重。针对评价指标(或属性)权重未知、属性评价值为三角模糊语言变量的供应商选择问题,进一步扩展了TOPSIS方法。
1 三角模糊语言变量
1.1 三角模糊语言变量的定义
定义1.1[11]:设S={si|i=1,2,…,t}为一种语言术语集(可看成语言标度集合),其中si表示一个语言术语,即语言变量的一个值,t为正整数,s1和st分别表示实际使用中语言术语集的下限和上限。一般,若sm和sn属于S,且m 定义1.2[12]:若sm和sn是语言术语集S中的两个语言术语,则它们之间的距离为 d(sm,sn)=|m-n|。 (1) 式(1)中m,n为语言术语的下标。 (2) 式(2)中,sl,sm,sn∈S,且sl 图1 三角模糊语言变量的隶属函数Figure 1 Membership function of triangular fuzzy language variables (3) 这些性质容易理解,且证明过程简单,这里就不赘述了。 根据文献[13]提出的一种模糊区间数的可能期望的定义,可以推理得出: (4) 为三角模糊语言变量的期望值。 采用基于熵值的权重计算方法确定评价指标的权重。决策者群体对同一备选供应商在同一属性下的评价越一致,则关于该备选供应商在该属性下的决策结果越有效,该属性应该赋予较大的权重;反之,则赋予该属性较小的权重[14]。利用信息熵来衡量决策者群体在某个属性下评价结果的一致性,熵值越大,表明评价结果越一致,属性权重也越大。属性权重的具体计算方法如下。 通过期望值计算公式,对三角模糊语言变量进行去模糊化处理,然后计算决策者群体关于备选供应商Ai在属性Cj下的期望值的信息熵Hij: (5) 从而得到决策者群体关于备选供应商集在属性Cj下的平均信息熵Hj: (6) 最后得到属性Cj基于熵值的属性权重计算公式为 (7) 根据上述给出的有关三角模糊语言变量的定义和运算法则,以及属性权重的计算方法,采用模糊TOPSIS方法进行供应商的选择,该方法的决策步骤如下。 (8) (9) 6)计算接近度CCi: (10) 7)根据相对接近度CCi按递减顺序定义备选方案的排名,CCi越大表示对应的方案与理想方案越接近。 具体决策步骤如下。 1)将3个决策者给出的模糊决策矩阵整合,见表1。 表1 3位决策者给出的4个企业不同属性下的评价值 表2 决策者关于各企业在各属性下评价值的期望值 表3 决策者群体关于各企业在各属性下的信息熵 表4 各企业在各属性下的综合决策评价值 3)根据步骤2)计算出的属性权重向量w=(0.203,0.201,0.197,0.201,0.198),与模糊综合矩阵相乘,构成的加权决策矩阵如下: 4)根据加权决策矩阵,确定正理想方案V+和负理想方案V-。 V+=[(s1.083,s1.353,s1.759) (s0.737,s1.005,s1.407) (s0.394,s0.788,s1.116) (s1.340,s1.541,s1.742) (s0.924,s1.254,s1.452)], V-=[(s0.609,s1.015,s1.353) (s1.072,s1.340,s1.608) (s0.985,s1.313,s1.707) (s0.938,s1.206,s1.474) (s0.858,s1.122,s1.386)]。 d1+=0.656,d2+=0.754; d3+=1.250,d4+=1.080; d1-=1.146,d2-=1.138; d3-=0.472,d4-=0.775。 6)根据式(10)计算各备选方案的相对接近度。 CC1=0.636,CC2=0.601, CC3=0.274,CC4=0.418。 由上述可知,相对接近度大小顺序为CC1>CC2>CC4>CC3,得出备选供应商的排序为:A1>A2>A4>A3。因此,所有备选供应商中最好的选择是供应商A1。 基于语言变量或不确定语言的决策是多属性决策的一个重要领域,本文主要采用基于三角模糊语言变量的模糊TOPSIS法来解决供应商选择这一多属性决策问题。文中首先介绍了三角模糊语言变量的基本概念和运算法则,提出了三角模糊语言变量的距离和期望值的计算公式,在此基础上利用信息熵法来确定属性权重,运用模糊TOPSIS方法对备选供应商进行综合评价。最后,通过一个算例证明了该方法的有效性。这表明该方法应用于实际的供应商选择问题中具有可行性,对决策者选择供应商有参考作用。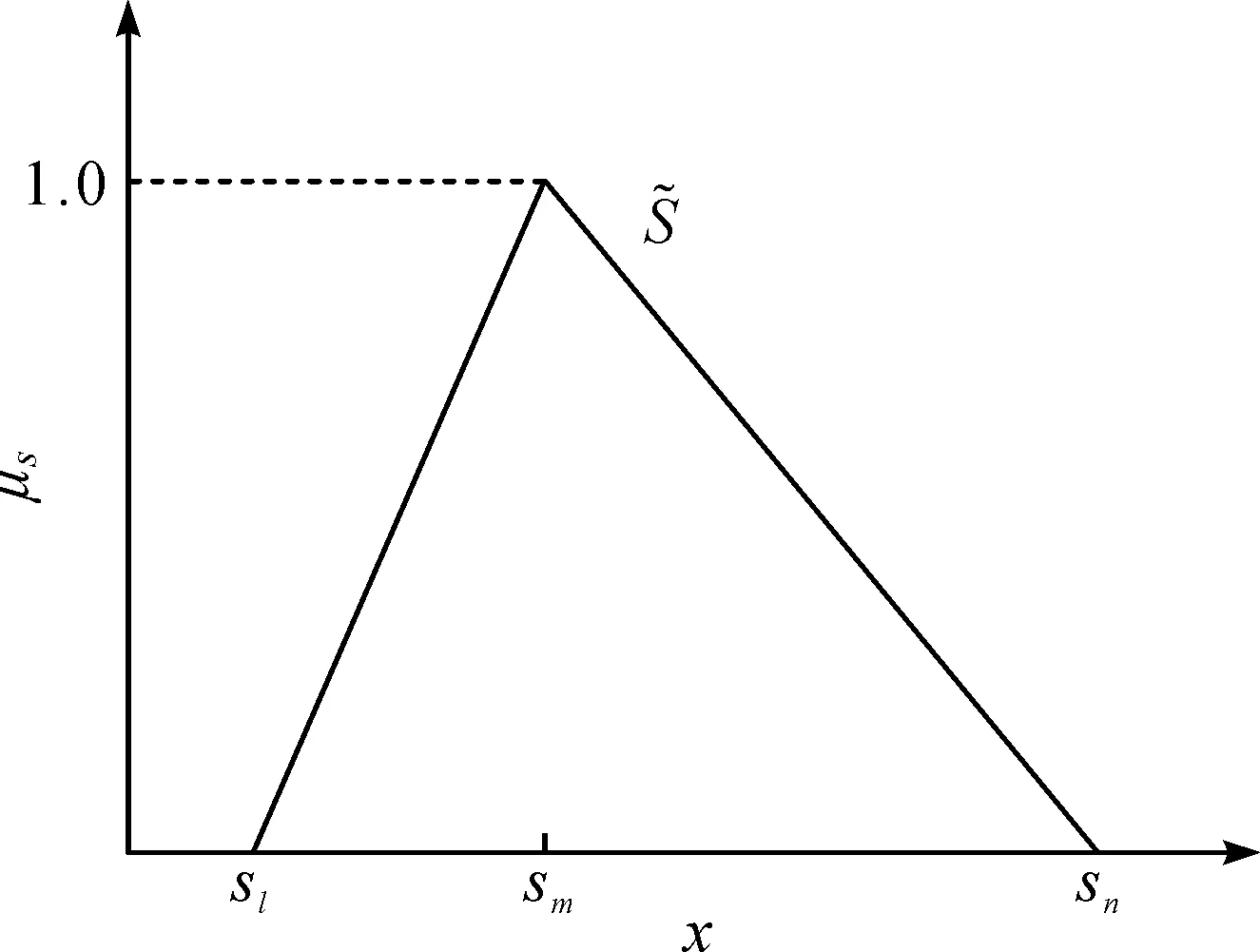
1.2 三角模糊语言变量的运算法则
1.3 三角模糊语言变量间距离的定义
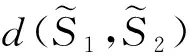

1.4 三角模糊语言变量的期望值
2 基于三角模糊语言变量的TOPSIS决策方法
2.1 问题描述
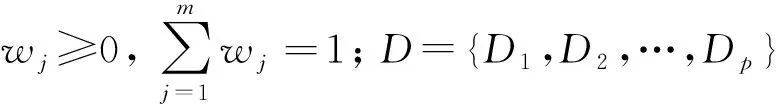
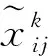
2.2 基于熵值确定属性权重
2.3 基于三角模糊语言变量TOPSIS法的决策步骤



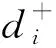
3 算例分析






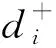
4 结 论
