槽式集热器反射镜抛物变形对允许跟踪误差的影响

王显龙，姚 远，李华山，王令宝，马伟斌，秦汉时

槽式集热器反射镜抛物变形对允许跟踪误差的影响

王显龙1，姚 远1，李华山1，王令宝1，马伟斌1，秦汉时2

（1.中国科学院广州能源研究所，广东 广州 510640；2.国网电力科学研究院，湖北 武汉 430074）

为了更好地指导太阳能槽式集热系统的设计和高效运维，本文研究了反射镜抛物变形对集热器允许跟踪误差的影响。首先定义了宽焦比、焦偏比、焦点偏离率3个无量纲参数，理论分析了理想状态不同尺寸下槽式集热器允许跟踪误差，进而给出反射镜剖面抛物变形后的允许跟踪误差的变化；同时计算宽焦比、焦偏比、聚光比对允许跟踪误差的影响并作图，给出基于不同几何参数的槽式集热器在不同变形量下的允许跟踪误差变化及其最大变形量尺寸。结果表明：宽焦比为4时槽式聚光集热器理论允许跟踪误差最大；3个无量纲数耦合影响决定允许跟踪误差的大小，且“膨胀”变形更加不利于集热器聚光。基于本文给出的图表，可预测集热器聚光损失并设计适宜跟踪系统，助力槽式太阳能热利用系统的推广。

太阳能；槽式集热器；抛物变形；允许跟踪误差；聚光比；宽焦比；焦偏比；焦点偏离率

槽式聚光集热技术是太阳能中高温热利用的主要途径之一，近年来得到大力研究和推广[1-7]，其研究方向主要集中在系统分析[1-3]、性能评价[4-6]和系统设计[7-8]等方面。跟踪精度是槽式集热系统设计和运维的重要参数，得到了较深入的研究[9-11]。Yusie Rizala和Chong等人[12-14]对太阳能跟踪方法和算法进行了介绍。Mussard等人[15]对1 m×1.05 m反射板开口0.5 cm吸热管槽式集热器的跟踪精度影响进行了模拟计算。Fabienne Sallaberry等[16]对某个型号槽式集热器的跟踪程序进行模拟分析并给出了计算结果。王金平等[17]设计了一种槽式太阳PLC跟踪控制系统，并对其跟踪精度和系统误差进行理论分析。Arian Bahrami等[18]基于所采集的相同地面高度的欧洲和非洲太阳能辐射数据，分析了纬度对不同太阳跟踪器性能的影响。胡亮等[19]分析了利用光控校正程控技术提高跟踪精度的理论，并确认PD调节器更有效。邵磊[20]和陆永亚[21]分别对蝶式太阳能跟踪误差和塔式聚光跟踪误差及风载荷的影响因素进行了分析。这些文献主要针对集热系统性能测试、集热器跟踪算法、跟踪外部影响因素、某一型号集热系统的跟踪精度等进行研究，鲜有文献对反射板变形的影响进行分析。

本文理论分析了理想状态下不同几何参数整体成型的中小槽式集热器的允许跟踪误差，并计算了中小型槽式聚光集热器整体成型反射板抛物变形对允许跟踪误差的影响。

1 理想状态下允许跟踪误差

槽式集热器剖面示意如图1所示。槽式反射面采光宽度为，吸热管吸热体外径为，焦距为。太阳光入射到地面为圆锥光束，夹角约为0.54°。

图1 槽式聚光集热器尺寸

反射板的最远端点垂直入射光线经过槽式反射镜反射后的最大偏移角度为，为点到吸热管中心的距离，为保证太阳光线完全入射到吸热管，则允许最大跟踪误差a为[19]：

由图2可以看出：相同的理想状态下，槽式集热器允许的最大跟踪误差随着的提高而减小；相同情况下，允许的最大跟踪误差随着的提高先增加后减小，这是因为虽然随着减小会降低，但由于的设计要求使得吸热管直径也降低；越高则允许跟踪误差的增减变化速度越快，在较大的情况下槽式集热器设计参数中的不能过小，否则即使在理想条件下太阳光也不能全部聚光（允许跟踪误差小于0）；随着的增加，允许跟踪误差大于0的起始数值也会增加。

通过求导式(4)可知：在为4的情况下允许跟踪误差值最大；在大于25.25、32.38、45.12、74.41情况下，对应任何的允许跟踪误差均小于2.0°、1.5°、1.0°、0.5°。

2 反射镜抛物变形对焦点位置影响

槽式反射镜会因为磨具加工误差、热弯成形误差、环境气温变化导致支架热胀冷缩等原因发生镜面变形，进而导致槽式集热器允许的最大跟踪误差变小。本文通过计算分析反射镜剖面整体变形因素对允许跟踪误差的影响。计算假设：整体变形后的反射镜左右两个端点以及吸热管位置不变，反射镜中点为最大变形点，剖面最大变形量为，其变形坐标为（0,），且反射镜变形后的剖面形状仍为抛物线。反射镜变形后的剖面抛物线方程变为式(5)，抛物变形标注如图3所示。

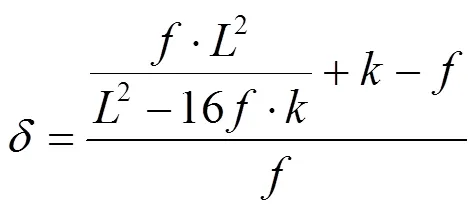
分别将10个代表性值和12个代表性值代入式(7)，计算结果见表1，且基于式(7)得到和对影响如图4所示。

由表1和图4a)可以看出，在不同下随着的提高，的变化越来越小，尤其在大于1时，的变化数值较小。这是由于通常较大，由式(7)可知只有在小于1时分母变化较大且更可以接近1，进而导致计算结果变化较大。

由图4b)和图4c)可以看出：随着绝对值的增大，的变化逐渐减小；绝对值相同时且为正值，变化更大。这是因为值大时，为正值式(7)中的分母比为负值时小，且式中第一项为正值，导致绝对值更大，变化也更大。

表1 反射镜焦点偏离率计算结果

Tab.1 The calculation results of focus deviation rate of the PTC reflector ×10–4

图4 b 和e 对d 影响

在不变的情况下，随着的增大，式(7)中的分母趋向无穷，因而可以认为最终趋向于的倒数。的增大代表变形导致的太阳光聚光误差增大，允许跟踪误差降低，可见相同中心变形距离下，槽式反射镜变形“收缩”（反射镜剖面中点向焦点方向变形移动）的影响要高于“膨胀”（反射镜剖面中向焦点背离方向变形移动）。由式(7)也可以看出，的大小对没有影响，即反射镜抛物变形导致的焦点偏离仅仅受反射镜的变形距离和的影响。

3 反射镜抛物变形对允许跟踪误差的影响

反射镜最远端点与变形反射后新焦点连线及变形前的原有焦点连线的夹角∠'，以1代替，（图3）定义为焦点最大偏离角，表示为

在反射境剖面抛物变形后槽式集热器允许的最大跟踪误差为

–1≥0.27 (a≥1) (13)

可见，反射镜抛物变形量如果超过某个确定值，则反射镜在任何角度下都不能将所有的太阳光反射到吸热管上，进而降低槽式集热系统太阳能光热效率。由式(12)可以看出，的大小对焦点最大偏离角没有影响。由式(13)可知，在某个特定尺寸情况下，抛物变形导致的最大跟踪误差值为此尺寸所采用聚光比的允许理想最大跟踪误差值减去焦点最大偏离角值。由式(12)计算得到和对焦点最大偏离角影响结果见表2，以此绘制出其影响曲线如图5所示。

表2和对焦点最大偏离角影响

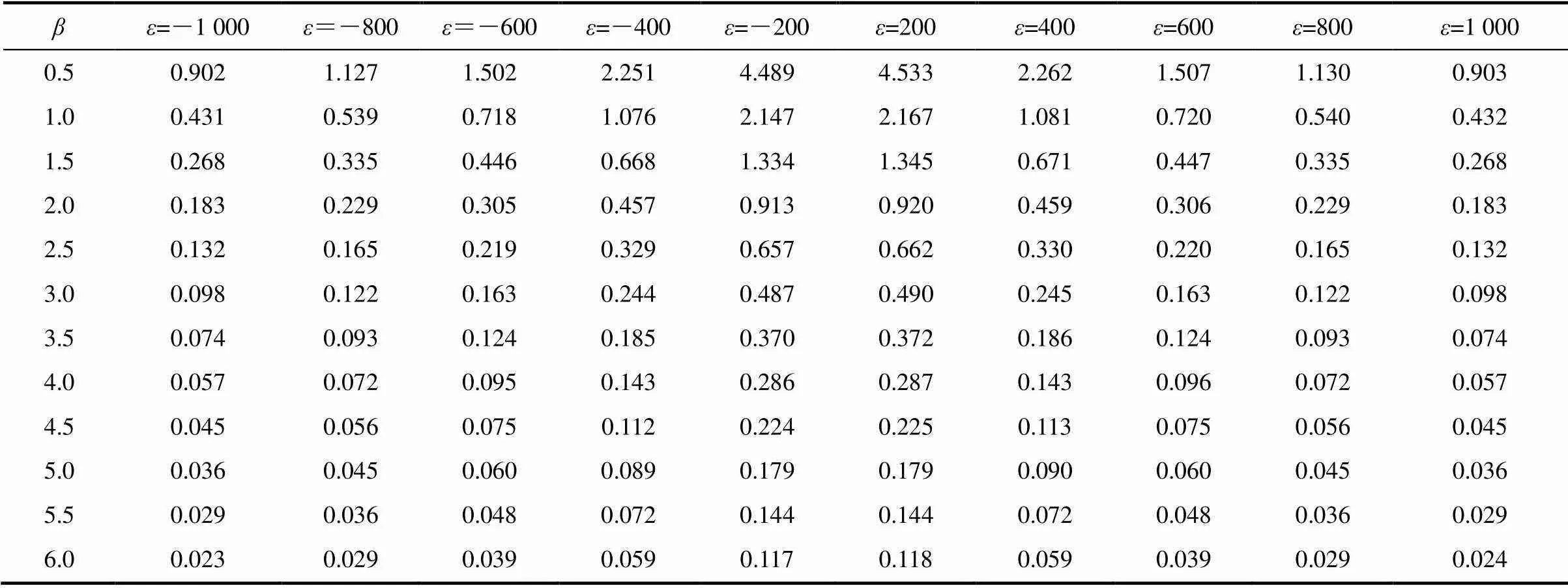
Tab.2 The influence of width focus ration and focus deviation ratio on the maximum focus deviation angle

由表2和图5可以看出，和对焦点最大偏离角均有较大影响。随着的提高和绝对值的增加，焦点最大偏离角减小，相同绝对值下的正负所引起的焦点最大偏离角的变化非常小。

图5 b 和e 对焦点最大偏离角影响曲线

将图2和图5整合得到、、对抛物变形允许跟踪误差的影响，结果如图6所示。由图6可见：当抛物变形导致焦点最大偏离角值大于特定聚光比理想跟踪误差值时，任何跟踪系统都不能将太阳光全部反射到吸热管上；相同下，随着的增加和的减小，抛物变形后的允许跟踪误差减小。

图6 抛物变形允许跟踪误差

4 结 论

1）理想状态下，槽式集热器的允许跟踪误差值最大对应的宽焦比为4，且随着聚光比的增大，宽焦比4对应的允许跟踪误差变化率会迅速增大，其宽焦比的上下限差值也会迅速降低。

2）反射镜抛物变形会导致集热器焦点偏离，相对而言“膨胀”变形更不利于集热器聚光。

3）通过作图给出特定参数下的不同变形量对应的允许跟踪误差，可有效帮助设计人员和使用客户基于使用地的冬夏温差匹配适宜跟踪系统，并为槽式聚光集热器的运维提供帮助

［1］ DESIDERI U, ZEPPARELLI F, MORETTINI V, et al. Comparative analysis of concentrating solar power and photovoltaic technologies: Technical and environmental evaluations[J]. Applied Energy, 2013, 102: 765-784.

［2］ QUASCHNING V. Technical and economical system comparison of photovoltaic and concentrating solar thermal power systems depending on annual global irradiation[J]. Solar Energy, 2004, 77: 171-178.

［3］ 黄予春, 曹成涛, 顾海. 基于IKFCM与多模态SSO优化SVR的光伏发电短期预测[J]. 电力系统保护与控制, 2018, 46(24): 96-103.HUANG Yuchun, CAO Chengtao, GU Hai. Short-term photovoltaic power generation forecasting scheme based on IKFCM and multi-mode social spider optimization SVR[J]. Power System Protection and Control, 2018, 46(24): 96-103.

［4］ CONRADO S L, RODRIGUEZ-PULIDO A, CALDERÓN G. Thermal performance of parabolic trough solar collectors[J]. Renewable and Sustainable Energy Reviews, 2017, 67: 1345-1359.

［5］ BELLOSA E, TZIVANIDISA C, BELESSIOTIS V. Daily performance of parabolic trough solar collectors[J]. Solar Energy, 2017, 158: 663-678.

［6］ 高志强, 李松, 周雪松, 等. 线性自抗扰在光伏发电系统MPPT中的应用[J]. 电力系统保护与控制, 2018, 46(15): 52-59.GAO Zhiqiang, LI Song, ZHOU Xuesong, et al. Design of MPPT controller for photovoltaic generation system based on LADRC[J]. Power System Protection and Control, 2018, 46(15): 52-59.

［7］ HAFEZA A Z, ATTIAA A M, ELTWABA H S, et al. Design analysis of solar parabolic trough thermal collectors[J]. Renewable and Sustainable Energy Reviews, 2018, 82: 1215-1260.

［8］ 傅金洲, 孙鸣. 基于气候条件的光伏储能一体发电系统的能量管理策略[J]. 电力系统保护与控制, 2018, 46(24): 142-149.FU Jinzhou, SUN Ming. Energy management strategy based on weather condition for photovoltaic-energy storage integrated power system[J]. Power System Protection and Control, 2018, 46(24): 142-149.

［9］ ZHAO D M, XU E S, WANG Z F, et al. Influences of installation and tracking errors on the optical performance of a solar parabolic trough collector[J]. Renewable Energy, 2016, 97: 197-212.

［10］ SALLABERRY F, JALÓN A G, TORRES J L, et al. Optical losses due to tracking error estimation for a low concentrating solar collector[J]. Energy Conversion and Management, 2015, 92: 194-206.

［11］ 李响, 范建业, 曹丽璐, 等. 大型光伏电站并网适应性分析[J]. 电力系统保护与控制, 2018, 46(8): 164-169.LI Xiang, FAN Jianye, CAO Lilu, et al. Analysis on the adaptability of large-scale grid-connected PV station[J]. Power System Protection and Control, 2018, 46(8): 164-169.

［12］ RIZALA Y, WIBOWOA S H, FERIYADI A. Application of solar position algorithm for sun-tracking system[J]. Energy Procedia, 2013, 32: 160-165.

［13］ THARAMUTTAM J K, KEONG A. Design and development of an automatic solar tracker[J]. Energy Procedia, 2017, 143: 629-634.

［14］ CHONG K K, WONG C W. General formula for on-axis sun-tracking system and its application in improving tracking accuracy of solar collector[J]. Solar Energy, 2009, 83: 298-305.

［15］ MUSSARD M, NYDAL O J. Influence of solar tracking inaccuracy and sun rays modeling on the efficiency of a small-scale parabolic trough[J]. Energy Procedia, 2014, 57: 1508-1515.

［16］ SALLABERRY F, PUJOL-NADAL R, LARCHER M, et al. Direct tracking error characterization on a single-axis solar tracker[J]. Energy Conversion and Management, 2015, 105: 1281-1290.

［17］ 王金平, 王军, 冯炜, 等. 槽式太阳能跟踪控制系统的研制及应用[J]. 农业工程学报, 2015, 31(2): 45-52. WANG Jinping, WANG Jun, FENG Wei, et al. Development and application of sun-tracking control system for parabolic trough solar collector[J]. Transactions of the Chinese Society of Agricultural Engineering, 2015, 31(2): 45-52.

［18］ BAHRAMI A, OKOYE A O, ATIKOL U. The effect of latitude on the performance of different solar trackers in Europe and Africa[J]. Applied Energy, 2016, 177: 896-906.

［19］ 胡亮, 彭佑多, 谭新华, 等. 太阳能“程控+光控”跟踪误差校正分析[J]. 计算机工程与应用, 2015, 51(10): 257-260. HU Liang, PENG Youduo, TAN Xinhua, et al. Solar “programmed+light control” tracking control system in photoelectric detector error correction analysis[J]. Computer Engineering and Applications, 2015, 51(10): 257-260.

［20］ 邵磊. 碟式太阳能自动跟踪系统传动机构误差研究[D]. 兰州: 兰州理工大学, 2014: 33. SHAO Lei. The research of driving mechanism errors of dish solar auto-tracking system[D]. Lanzhou: Lanzhou University of Technology, 2014: 33.

［21］ 陆永亚. 塔式定日镜受风载荷和跟踪误差影响的聚光效率特性研究[D]. 重庆: 重庆大学, 2013: 38. LU Yongya. Focusing efficiency characteristics of the tower heliostat under the influence of wind load and tracking error[D]. Chongqing: Chongqing University, 2013: 38

Influence of reflector deformation on allowed tracking error of parabolic trough collector

WANG Xianlong1, YAO Yuan1, LI Huashan1, WANG Lingbao1, MA Weibin1, QIN Hanshi2

(1. Guangzhou Institute of Energy Conversion, Chinese Academy of Sciences, Guangzhou 510640, China; 2. State Grid Electric Power Research Institute (Wuhan) Energy Efficiency Evaluation Co., Ltd., Wuhan 430074, China)

To better guide the design and efficient operation and maintennce of solar trough collector system, the influence of the reflector’s parabolic deformation on the allowed tracking error of the collector is investigated. Three dimensionless parameters, such as width focus ratio, focus deviation ratio and focus position deviation rate, are defined. The ideal allowed tracking error of the parabolic trough collector in different sizes is calculated, and the allowed tracking error variation with parabolic deformation of the reflector are given. Moreover, the effect of wide focus ratio, focal deviation ratio and concentration ratio on the allowed tracking error is calculated, and the result is drawn, then the variation of the allowed tracking error and the maximum deformation size are given based on different geometric sizes. The calculation results show that, the theoretical allowed tracking error reaches the maximum when the width focus ratio is 4, the coupling effects of the above three dimensionless parameters determine the value of the allowed tracking error, and the“expansion”deformation is unfavorable for the collector optical concentration. On the basis of the chart given in this paper, the concentrating loss of the collector can be predicted and the suitable tracking system can be designed to promote the application of the parabolic trough solar thermal utilization system.

solar energy, parabolic tough collector, parabolic deformation, allowed tracking error, concentration ratio, width focus ratio, focus deviation ratio, focus position deviation rate

TK513.1

A

10.19666/j.rlfd.201812187

王显龙, 姚远, 李华山, 等. 槽式集热器反射镜抛物变形对允许跟踪误差的影响[J]. 热力发电, 2019, 48(7): 86-91. WANG Xianlong, YAO Yuan, LI Huashan, et al. Influence of reflector deformation on allowed tracking error of parabolic trough collector[J]. Thermal Power Generation, 2019, 48(7): 86-91.

2018-12-10

广东省科技计划项目(2017A030223009)；广东省自然科学基金项目(2018A0303130181)；国家电网公司总部科技项目(SGHB0000KXJS1800477)；中国科学院可再生能源重点实验室基金(Y807J21001)

Supported by：Science and Technology Planning Project of Guangdong Provice (2017A030223009); Natural Science Foundation of Guangdong Provice (2018A0303130181); State Grid Corporation Headquarters Science and Technology Project (SGHB0000KXJS1800477); Key Laboratory Foundation of Renewable Energy, CAS (Y807J21001)

王显龙(1979—)，男，硕士，高级工程师，主要研究方向为太阳能热利用和节能余热利用技术，wangxl@ms.giec.ac.cn。

（责任编辑 杨嘉蕾）