面向图匹配的属性关系图模型

姚 强，朱 明，唐 俊，张 艳(安徽大学电子信息工程学院，合肥23060)

2(偏振光成像探测技术安徽省重点实验室，合肥230031)E-mail:zhuming@ahu.edu.cn

1 引言

图像匹配［1，2］是计算机科学理论中的一个基本问题，它涉及计算机视觉、模式识别和机器学习等各个研究领域［3-5］.利用图模型［6-8］描述图像特征点间的空间结构关系完成匹配是近年来的研究热点，它将图像的结构匹配问题转化为图匹配问题，图匹配方法包括模型构建和优化算法两部分.Leordeau 等［9］提出一种谱匹配算法(Spectral Matching，SM)，该算法首先为待匹配点集构造分配图，并利用成对约束条件构造相应的亲邻矩阵，然后用谱分解方法获得亲邻矩阵的最大特征值对应的特征向量，最后利用此特征向量实现点集之间的匹配.Aguilar等［10］提出一种图变换匹配算法(Graph Transformation Matching，GTM)来实现特征点匹配，首先对两幅图像的特征点集构造k近邻图，然后根据一个准则去除离群点后，迭代地更新近邻图.文献［11］提出一种迭代投影的匹配方法，该方法主要是在优化匹配目标函数的过程中，通过迭代投影，使得匹配的解最终能够满足匹配问题的约束要求.文献［12］对相关点集构造赋权完全图，再对每个点关联的部分边构造线图，然后根据线图的Laplacian矩阵分解后的特征值计算特征点间的匹配概率，最后通过KM算法求得最优匹配.Yang［13］等提出了距离、方向矩阵和凸凹松弛求解策略，但是由所有特征点的中心位置构造的参考方向，在图像形变较大时存在较大偏差，导致匹配效果不好.文献［14］在边的属性上考虑了方向性，提出了可用于无向图和有向图的亲和度矩阵分解方法和对目标函数求解的方法.在大多数图模型的构造中，对于特征点和边的初始描述都是基于距离或者角度信息，但它们对图像形变较大的场景下是敏感的，在边上考虑了方向信息可以提高模型的信息量，但简单而有效的，对图像之间的变换具有不变、鲁棒的特征描述是所有基于特征的匹配方法中的核心问题.

为了提高图像匹配的精度和匹配方法的适应能力，本文提出了一种面向图匹配的属性关系图模型，利用图像中特征点相对于特征中心点的分布情况为特征点设定属性，根据特征点连线两侧的点数作为边的属性值，并可以为边增加方向信息，以此构造图像之间的亲和矩阵，然后根据整数约束下的迭代求解算法求解匹配问题.提出的特征模型能很好地描述图像中特征点间和边间的关联信息，通过整数约束下的迭代求解算法能够求得高正确率的匹配矩阵.

2 基本概念

图能够很好地描述图像中目标的结构信息.设属性关系图G是由有限个非空的顶点集合V和节点间对应的边的集合E及顶点和边属性组成的四元组，记作G=(V，E，A，R)，V={v1，v2，…，vn}，n=|V|表示顶点或者节点的个数，E={e1，e2，…，em}，m=|E|表示图G边的个数，对于属性关系图G，图的每个顶点vi∈V都赋有特征点属性值ai∈A，图的每条边eij∈E也赋有关系属性值rij∈R.为了实现两个属性关系图的顶点匹配，首先要定义两个图的顶点间和边之间的相似性或者亲密性.

所以对无向图的边进行定向，可使图像间的结构信息更加丰富.在单有向图上使用两个特征点间的一些属性值的大小来设定边的方向，不仅可以区分出边eij和eji的属性不同，即rij≠rji，同时还可以隐含着有关特征点属性值的大小关系信息.在这种情况下也可得到两幅图像间的不对称的亲和矩阵 K，即

3 属性关系图模型

图模型是一种典型的结构描述模型，除了节点本身，它还可以描述节点与节点之间的关系.属性关系图是用来描述两图间顶点与顶点间，边与边之间的相关性，大多数构造方法是基于两个边的边长或者角度的关系，不适应于图像形变较大的情况下，所以简单而有效的描述方法是十分必要的.

因为在图像发生的各种变换下，比如旋转、尺度变换等，图像的特征点都会随着图像做变换，即各个特征点之间的相对方位基本是不变的，如图1所示，V1={v1，v2，…，vn}是左边图G1中的特征点集，o是点集的中心点.V2={v'1，v'2，…，v'n}是右边图G2的特征点集，O'是点集的中心点，vi指向vj的连线lij将左图G1分成两部分，其在右图G2上的匹配点v'i指向v'j的连线l'ij将图G2分成两部分，连线左边的特征点数目都为1，右边的特征点数目都为3.左图G1上vi指向O的连线lio将点集分成两部分，连线左侧的特征点数目为3，其对应的右图G2上v'i指向O'连线l'io左侧的特征点数目也为3.

图1 方向描述符的构造Fig.1 Construction of direction descriptors

在各种变换下，连线左边的点在变换后一般是不会出现在连线右边的，所以就保证了描述符的稳定性.使用特征点与特征中心点连线左侧的特征点数目作为特征节点的属性值，则亲和矩阵K的对角元素可由公式(2)计算得到.

其中，Nio表示图G1特征点vi面向中心点O的连线lio左侧的特征点数目，N'i'o表示图G2特征点v'i面向中心点O'的连线l'io左侧的特征点数目，γ是常数因子.

则亲和矩阵K的非对角元素可由式(3)计算得到，

其中，Nij表示图G1的特征点集中特征点vi面向特征点vj的连线lij左半部分的特征点的总数目，则N'i'j'表示图G2的特征点集中特征点v'i面向特征点v'j的连线l'ij左半部分的特征点的总数目.对于连接线上的S(S≥2)个点，用特征中心点O的位置判断，即对于在连线上的点，如果特征点中心在连线的左侧，则计算的特征点数目增加S个.由于Nij≠Nji，则亲和矩阵K 是非对称的.

属性关系图模型匹配问题可用以下数学模型来描述，即

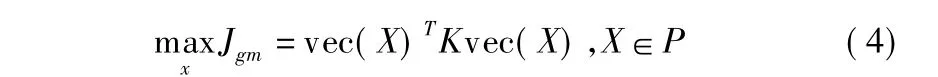
其中，置换矩阵X∈P保证了图顶点匹配的一对一约束，P是置换矩阵集合，满足式(5).

文中采用整数约束下的迭代求解方法［15］求解该匹配的数学模型，从而得到匹配结果.该整数约束下的迭代求解方法是以任意初始解vec(Xk)为输入，通过迭代求解的方法，寻找满足式(4)所示约束下的最优解.

4 算法流程

根据式(1)-式(3)可计算得到图G1和图G2间的亲和矩阵K，考虑到图G2相对于参考图G1可能存在镜像变换，在对参考图G1求顶点和边的属性时，利用连线左侧的特征点求顶点和边的属性，对于图G2会分两种情况，一种是利用连线左侧的特征点数目计算顶点和边的属性，另一种是利用连线右侧的特征点数目计算顶点和边的属性，所以在两种不同情况下会得到两种不同的亲和矩阵K1和K2，然后采用整数约束下的迭代算法求解对应的匹配置换矩阵X1和X2，并可得到对应的目标函数值J1和J2，根据比较目标函数值，选择最大目标函数值对应的置换矩阵作为最终的匹配矩阵，从而得到两幅图像间特征点的匹配对应关系.本文算法的具体流程如下:

1)对于图 G1和图 G2的特征点集 V1={v1，v2，…，vn}和，分别求出两点集的中心点 O 和 O'.

2)求出V1特征点集中的所有特征点与中心点O连线的左侧的特征点数目和V2特征点集中特征点与中心点O'连线的左侧的特征点数目，按照公式(2)计算得到亲和矩阵K1的对角元素值.再根据V1中特征点与中心点O连线的左侧特征点数目和V2特征点集中特征点与中心点O'连线的右侧的特征点数目，按照公式(2)计算得到亲和矩阵K2的对角元素值.

3)对于V1和V2特征点集，求出所有不同特征点之间的连线左侧的特征点的数目，然后根据公式(1)和公式(3)求出亲和矩阵K1的非对角元素值.

4)然后根据亲和矩阵K1，并采用整数约束下的迭代求解方法得到置换矩阵X1，计算得到对应的目标函数值J1.

5)对于V2特征点集，求出所有特征点之间的连线右侧的特征点的数目，结合V1特征点集中特征点间连线左侧的特征点数目，根据公式(1)和公式(3)求出亲和矩阵K2的非对角元素值，并求出对应的置换矩阵X2和对应的目标函数值J2.

6)比较J1和J2的值，选择大的目标函数值对应的置换矩阵作为最终匹配矩阵，输出匹配结果.

5 实验及结果分析

为验证文中算法的性能，选用 SM 算法［16］、PM 算法［17］、FGM 算法［14］、Yang 算法［13］与文中算法 Ours进行对比.Yang算法中距离矩阵和方向矩阵的权值都为0.5.实验分为在House数据集和真实图像数据集上的实验.

5.1 House图像数据集匹配

CMU数据图像库中的House图像序列经常被用于测量图匹配算法的性能，这个数据集由111个房屋组成，每个房屋上都有对应的30个特征点，以0序列图像作为参考图像，以0:10:110的帧间隔图像作为待匹配图像，计算得到各算法的匹配正确率.几种算法关于匹配正确率的对比结果如图2所示.

图2 几种算法在house图像上的匹配正确率对比Fig.2 Comparison of matching accuracy of several algorithms on house image

由图2可知，随着图像间帧数的增加，House图像间得形变变大，PM、SM算法的匹配正确率呈现明显的下降趋势，Yang算法只在110帧时出现了错误的匹配对，在所有的House图像序列上，文中Ours算法和FGM算法都考虑了方向信息，它们的匹配正确率都等于1，都是完全正确的.

5.2 真实数据图像匹配

为了进一步测量算法在形变较大的图像上的匹配性能，采用四组真实实验数据的序列图像进行实验，如图3所示，第一、三、四组是来自Mikolajczyk测试数据集的包含视点变化的“graf”图像和包含尺度和旋转变换的“bark”和“boat”图像，第二组为 MorelYu数据集中包含尺度和经度变化的“paint”图像，每组序列图像中各取5幅逐渐变化的图像，随着序列数的增加图像的形变逐渐变大.

图3 真实实验数据图像Fig.3 Real experimental data image

在四组序列图像上手动提取特征点对，对于第一组和第四组的序列图像分别提取60个特征点，对于第二组序列图像分别提取35个特征点，对第三组序列图像分别提取30个特征点.对所有特征点集的顺序随机打乱，几种算法在真实图像上关于正确率的实验对比结果如表1所示.

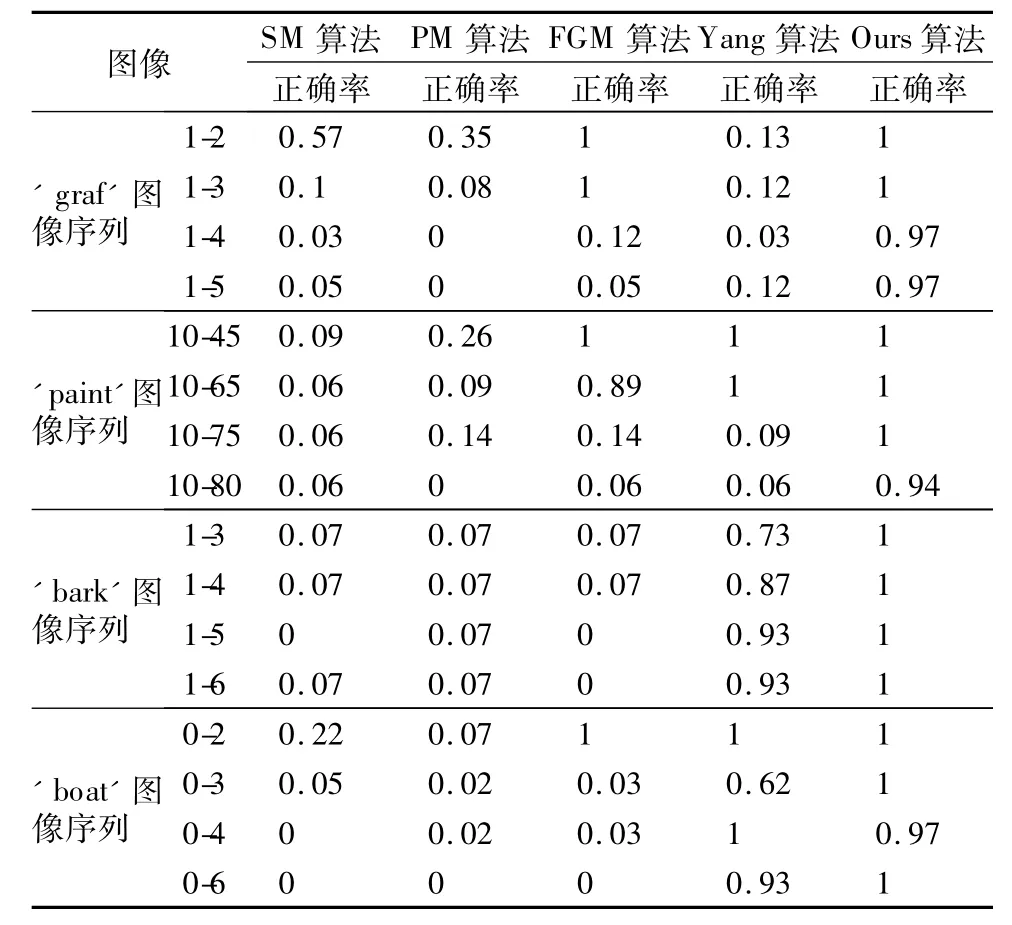
表1 几种算法关于匹配正确率的对比Table 1 Comparison of matching accuracy with several algorithms

随着图像序列的增加，图像间的形变在逐步增大，由表1知，本文Ours方法在两组序列图像上的匹配正确率均是最高，其它算法匹配正确率在逐渐降低，逐渐趋于0，FGM算法在构造亲和矩阵的时候考虑了方向信息，Yang算法在构造邻接矩阵的时候也考虑了方向约束，这两个算法总的效果在除了文中Ours算法之外效果最好.在本文算法下对方向的判断标准对仿射变换是不变的，所以能保证在两幅图像间构造的亲和矩阵能准确的描述图像间边与边，点与点间的亲近值，在各类的图像变换类型下能保证具有较高的匹配正确率.图4为几种算法在序列图像上的匹配结果，其中图4(a)-(e)为本文Ours算法与Yang算法、DGM算法、PM算法和SM算法在“graf”的“1-5”序列图像上的匹配结果，图4(f)-图4(h)为本文 Ours算法在“paint”的“10-80”序列图像上、“bark”的“1-6”序列图像上和“boat”的“0-60”序列图像上的匹配结果.

图4 几种算法在真实图像上的匹配结果Fig.4 Matching results of several algorithms on real images

6 结束语

本文提出了一种面向图匹配的属性关系图模型，该模型利用特征点集的分布情况构造表示顶点之间和边之间属性的亲和矩阵，在构造边的属性时考虑了方向信息，并利用整数约束下的迭代求解算法求解匹配矩阵，得到特征点间的一对一匹配关系.实验结果表明，该属性关系图模型的图匹配算法有较好的匹配效果，且对于形变较大的图像也有很好的匹配效果.