基于BP神经网络的RFID室内定位算法研究

邓 昀，朱 彦，杨逸夫，程小辉，李朝庆1(广西嵌入式技术与智能系统重点实验室，广西桂林541004)

2(桂林理工大学信息科学与工程学院，广西桂林541004)

3(湖南商学院新零售虚拟现实技术湖南省重点实验室，长沙410205)

E-mail:woshidengyun@sina.com

1 引言

日常生活中，定位系统越来越重要，无线定位技术已然成为了当前研究的重点.在室外定位环境中，例如GPS全球定位系统，有着非常突出的优势，其定位准确率高，并且能实现实时定位，为人们的出行提供了很大便捷.但是在室内环境中［1］，GPS所需要的卫星信号会被建筑物等障碍物影响，导致其信号会变得极其微弱，甚至会被完全遮蔽，其定位性能远不能满足需求.因此，室内定位技术的研究有着重大的现实意义.目前常见的室内定位技术包括:无线局域网，超声波技术，红外线技术，以及射频识别技术(RFID)［2］.在这几种定位技术中，RFID技术有着低成本、非视距、非接触、高精度等优点，被广泛的应用在室内定位技术中［3-6］.因此，在最近几年中，RFID室内定位研究已经成为了一个热点问题.

2 系统建模

本文算法使用了基于nRF24LE1芯片的有源RFID标签来实现定位，标签工作原理是基于功率射频信号值，其提供4种离散的功率值，分别为－18dbm，12dbm，6dbm和0dbm，为了表述方便，本文将其定义为 P1，P2，P3，P4档，根据实验测量的结果，它们分别对应于最大的传输距离为4.5m，5m，5.5m，6m.因此在空旷的环境下，部署一个4m*6m的矩形定位区域用于本文的算法研究.取10个RFID标签作为参考标签，并将其按间隔2m的距离部署在矩形的边缘区域，一个目标标签用于传输数据，一个阅读器用于接收信号，一个便携式电脑用于数据的收集和存储.根据4个离散功率射频信号值最远传输距离间隔大约为0.5m的特点，将4m*6m的定位区域划分为96个小大相同、整齐排列的正方形网格，每个小正方形的边长为0.5m.如图1所示.

图1 数据采集和实验部署图Fig.1 Data acquisition and experiment deployment diagram

由虚线分隔而成的正方形网格为数据采集区域，取正方形的中心位置作为该正方形网格的计算坐标位置，用于计算本文算法的均方根误差.参考标签每隔2S为一个周期，广播其当前的功率射频信号值和自身的身份ID，其功能经初始化后定期将－18dBm、－12dBm、－6dBm和0dBm的功率射频信号值发送给目标标签，其广播顺序为 P1，P2，P3，P4，P1，….

基于BP神经网络的RFID室内定位算法分为两个步骤进行，其中第一步为采集数据，建立模型［7-9］.首先按照图1所示，部署实验测试环境，接着将目标标签放置在每一个正方形网格内采集多条数据，经过筛选，得到每个正方形网格内的指纹数据，最终形成96组指纹数据.收集96组指纹数据所对应的坐标位置.然后对指纹数据进行归一化处理，再使用kmeans聚类算法对4m*6m的定位区域划分为K个宏区域，得出每一个正方形网格所属宏区域的类标签.将由每一个正方形网格内收集到的指纹数据以及指纹数据所对应的类标签作为输入数据，进行SVM分类训练，建立最优的SVM多分类模型.针对具有相同类标签的正方形网格，利用BP神经网络算法，将属于相同类标签的指纹数据作为BP神经网络的输入数据，将每条指纹数据所对应的坐标位置作为BP神经网络的目标数据，进行BP神经网络训练，建立最佳的BP神经网络模型.其流程如图2所示.

基于BP神经网络的RFID室内定位算法的第二步为使用模型，实验仿真.首先在定位区域内放置待定位标签，采集待定位标签发送的数据，记录每条数据所对应的坐标位置，即其实际位置.对于采集到的数据进行归一化处理，将处理过后的数据作为输入数据，利用已经建立好的SVM分类器，得出每条数据所属的类标签.提取具有相同类标签的数据，并将其作为BP神经网络的输入数据，利用已经建立好的BP神经网络模型，预测出每条数据所对应的坐标位置.根据BP神经网络预测出的坐标位置和实际位置作比较，得出该算法的均方根误差，最后再画出误差累积概率分布图.

图2 建立模型流程图Fig.2 Establish model flow chart

3 BP神经网络定位算法设计

3.1 采集数据以及数据预处理

3.1.1 建立指纹数据库

本文对于4m*6m的区域划分了96个大小相等边长为0.5m的正方形网格.对该区域建立坐标系，横纵坐标代表的是每个正方形网格的坐标位置，对于每一个正方形网格，定义数据DG=(Pj1，Pj2，…，Pji)，为在该区域内收集到的指纹数据，其中i=1，2，…，10表示参考标签的身份ID，本文中参考标签数量为10 个，则 i最大为 10，j=8，10，12，14，16 表示收到标签i发出的功率值，为了实验的方便，易于数据的处理和管理，不和丢失值0冲突，本文把功率值为－18dbm，－12dbm，－6dbm和0dbm的数据做转换处理，其分别对应为8dbm，10dbm，12dbm，14dbm，对于没有接收到参考标签发送的功率值，即丢失值0，将其转换为16dbm，方便画图和管理数据.

令 G={(x1，y1)，(x1，y2)，…，(xa，yb)}表示正方形网格的坐标，令珟G={(珓x1，珓y1)，(珓x1，珓y2)，…，(珓xa，珓yb)}为本文收集数据和实验仿真的计算坐标，计算坐标为每一个小正方形的中心点，网格坐标表示的是指纹数据对应的网格位置，计算坐标表示的是目标标签的实际坐标，则用于计算实验的均方根误差，其中 a=1，2，…，12，b=1，2，…，8.网格坐标和其对应的计算坐标的转换公式如下:

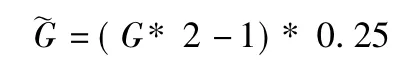
即:

用一个正方形网格来举例，例如本文在(10，6)位置共收集到80组数据，每个标签发送的功率档值的次数如表1所示.

16dbm代表在该位置没有收到参考标签发出的功率档，由

3.1.2 数据归一化

定义数据集F={D1，D2，…，DG}为本文所建立的指纹数据库，其中G=1，…，96表示正方形网格，对于每一个正方形网格有一条数据DG=.首先找出数据DG当中的最大值和最小值，然后把这些值规范到范围［0;1］内.定义:MAX={M1，M2，…，MG}，MIN={m1，m2，…，mG}分别为数据集F的最大值和最小值.对于每一个数据PGi表示的是在第G个正方形网格收到来自第i个参考标签发出的功率档，并按照公式(2)进行归一化处理.

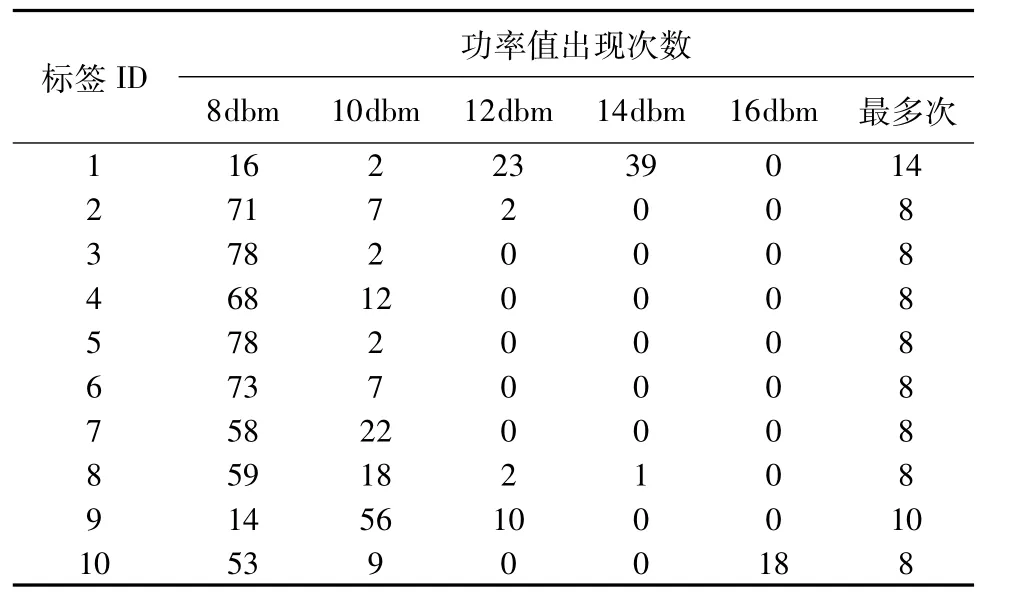
表1 (10，6)坐标位置数据Table 1 (10，6)Coordinate position data

3.2 使用K-means算法划分K类宏区域

本文则采用K-means算法将96个正方形网格定位宏区域划分为若干个宏区域，聚类过后每个网格都有一个类标签，从而使得指纹数据库建立得更为精确.

K-means算法总体思路如下:首先，由用户确定所要聚类的准确数目k，从n个数据样本{x1，x2，…，xn}中随机的选择K个点{c1，c2，…，ck}作为初始聚类中心，每个样本代表一个簇(类)的中心或均值，计算剩余样本到K个聚类中心的距离，根据距离相似原则对样本进行聚类，对剩余的每个样本，根据其与各簇中心的距离将它赋给最近的簇，然后重新计算每个簇内对象的平均值形成新的聚类中心，再继续聚类，这个过程重复进行，直到当前均值向量不再变化为止，即样本中每个数据点与它最近的聚类中心的距离平方和最小，最终得到基于 K-means算法的簇划分［10］.

本文K-means算法采用迭代更新的方法:在每一轮迭代中，都将样本中所有的点依据距离相近原则，划分为K个类，再重新计算每个聚类中所有样本点的平均值，并将其作为下一轮迭代的聚类中心.具体算法处理步骤如下:

输入:聚类数目K，96组指纹数据作为样本数据.

输出:K个聚类，每组数据所对应的类标签.

1)从96个数据样本中随机选择K个样本作为初始的聚类中心;

2)根据欧式距离相似准则，分别计算剩余每个样本到各个聚类中心的距离，并将每个样本分配到距离最近的类中;

3)当所有样本分配完成之后，再更新K个簇的均值或者中心点;

4)与前一次计算得到的K个聚类中心进行比较，如果聚类中心发生变化，则重新执行步骤2).如果K个聚类中心不再变化，且准则函数收敛，则执行步骤5);

5)输出聚类结果，得出每组数据所属的类标签.

将归一化后的96组指纹数据珘F={珟D1，珟D2，…，珟DG}作为输入样本，然后用K-means算法进行聚类，得出的输出结果为每条数据的类标签DLG以及所属正方形网格G的类标签，即:

这里将96个正方形网格，分别聚成2类宏区域，3类宏区域和4类宏区域.即K的取值为K=2，3，4.图3为K-means聚类过后划分3类宏区域图形.

图3 划分为3类宏区域Fig.3 Divided into 3 types of macro regions

通过划分的宏区域可以看到，正方形网格的分布极不规则，则需要通过建立SVM分类模型，进一步规范分类结果.

3.3 建立SVM多分类模型

通过K-means算法得出K个宏区域之后，根据其输出结果得出的96个类标签，和其对应的指纹数据用LIBSVM算法［11］进行模型的建立.建立多分类模型的步骤如下:

输入:96组指纹数据以及每组数据对应的类标签

输出:参数 c，g

1)将归一化后的96组指纹数据及其相对应的坐标位置作为SVM分类器的输入数据;

2)选用高斯核作为SVM算法的核函数;

3)采用网格搜索交叉验证方法得出最佳参数c和g;

4)利用选择好的参数对整个训练集进行训练，测试分类模型的准确率;

5)保存多分类模型.

具体流程图如图4所示.

图4 建立SVM多分类模型的流程图Fig.4 Establishing the flow chart of SVM multi classification model

使用SVM算法时，关键是找到最佳参数，本文使用RBF核作为核函数，RBF核中有2个参数:c和g.本文使用Grid Search(网格搜索)交叉验证方法，查找样本数据的最佳参数c和g，并得出分类的准确率.本文算法中使用了k折交叉验证法，将原始数据集按固定比例分为训练集与测试集，使用测试集来评估模型的好坏，并重复这个过程k次并使得数据集中所有数据都被划分为训练集与测试集.最后对k次验证结果求取平均值.在网格搜索算法中，是通过遍历所有的c和g的参数组合并进行k折交叉验证，从而得出最优的参数组合［12］.

当进行SVM模型建立的时候，需要训练和测试SVM分类器，本文把建立好的96组指纹数据分为80组训练数据和16组测试数据.每条训练数据和其对应的类标签作为SVM的输入数据，训练SVM分类器.测试数据则是用来测试SVM分类器的准确率，当输入一条数据时，SVM分类器输出结果为对应于这条数据的标签GL.当96个正方形网格被划分为2类，3类，4类宏区域之后，利用网格交叉验证方法得出来的最优参数和分类模型的准确率如表2所示，这里k折交叉验证法中，k=10.

表2 SVM分类模型参数取值和分类准确率Table 2 SVM classification model parameters and classification accuracy

3.4 使用BP神经网络模型预测目标标签的位置

3.4.1 确定K个BP神经网络结构

当数据被K-means算法聚成K类之后，则需要建立K个BP神经网络来建立学习模型.将所有具有相同类标签DLG的数据分类提取出来，并作为L类BP神经网络学习的输入数据，其对应的计算坐标(xˇ，珓y)则作为目标输出数据.

BP网络输入层的神经元数由输入向量的维数决定，输出层神经元数由输出向量的维数决定.本文把归一化后指纹数据珟Dx，y=(P珘1，P珘2，…，P珘i)作为输入数据，其对应的坐标位置作为目标输出数据，因此本文构建BP神经网络时，其输入层神经元数为10个，输出层神经元是为2个.由于三层神经网络具有很好的泛化性以及非线性能力，网络训练的效率也更快，并且在对BP神经网络调节仿真效果时，发现只有一层隐含层的神经网络就有着良好的拟合效果，满足本文实验的需求，因此本文使用隐含层层数为1的三层神经网络结构，然后逐步调节隐含层的神经元个数，观察其神经元个数从10逐渐增加时的拟合效果，经过多次实验和观察，得到在不同宏区域建立BP神经网络所对应的最佳隐含层神经元个数.如表3所示，为3类宏区域BP神经网络隐含层神经元.

表3 3类宏区域BP神经网络隐含层神经元Table 3 3 kinds of macro region BPneural network hidden layer neurons

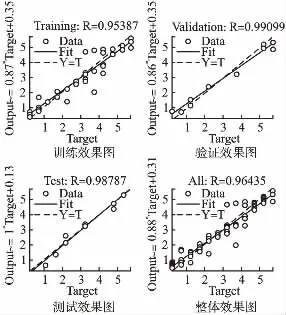
图5 3类宏区域BP1神经网络训练效果图Fig.5 3 kinds of macro area BP1 neural network training effect diagram

图6 3类宏区域BP2神经网络训练效果图Fig.6 3 kinds of macro area BP2 neural network training effect diagram

图7 3类宏区域BP3神经网络训练效果图Fig.7 3 kinds of macro area BP3 neural network training effect diagram

BP神经网络定位算法主要部分如算法1中描述.

算法1.BP神经网络定位算法

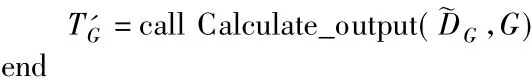
4 实验仿真

4.1 实验仿真过程

通过以上过程建立的模型，用实例来验证算法的可行性.仿真过程如下:

4)将具有相同类标签GL的数据提取出来，作为L类BP神经网络的输入数据.

5)利用已经建立好的K个宏区域BP神经网络模型进行坐标位置的预测，输出结果为预测的坐标位置

6)使用均方根(RMSE)误差E来衡量本文算法的好坏.E计算如公式(6)所示.

表4 不同宏区域的预测坐标位置Table 4 Location of predicted coordinates in different macro regions

即累计所有待定位标签的计算坐标和预测坐标，计算误差平均值.从119组数据中随机取20组数据，来进行算法的分析，20组数据的网格坐标及其计算坐标以及实验仿真后的预测坐标如表4所示，随机取得的20组数据可见，3类宏区域目标标签的预测值与目标标签的真实值较为接近.则由119组数据和公式(6)得出当划分不同宏区域时的均方根误差如表5所示.

表5 不同宏区域的均方根误差Table 5 Root mean square error in different macro regions

由表5可知，当将定位区域划分为3类宏区域时，其定位的准确率要高于其他两类，基本满足本文室内定位需求.

7)使用误差累积分布函数划出均方根误差的分布情况，如图8所示，划分2类宏区域时，均方根误差在1m以内的分布概率为60.5%，划分3类宏区域时，均方根误差在1m以内的分布概率为68.2%，划分4类宏区域时，均方根误差在1m以内的分布概率为59.6%.可见当划分为3类宏区域时，其均方根误差在1m以内的概率分布要明显高于其他两类，即其定位的准确率也明显高于其他两类.

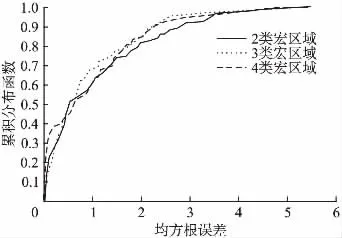
图8 均方根误差累计分布图Fig.8 Root mean square error cumulative distribution map

4.2 对比算法分析

传统的位置指纹定位算法仅采用BP神经网络作为匹配规则.本文将建立的指纹数据以及数据所对应的位置作为输入数据，建立BP神经网络，利用仿真阶段收集到的119组数据，进行传统BP神经网络算法的仿真，得出来的均方根误差为1.094m，如表6所示，可以看出本文的定位算法优于传统的BP神经网络定位算法.

表6 不同宏区域的均方根误差Table 6 Root mean square error in different macro regions

5 总结

本文针对一种基于廉价nRF24l01芯片的RFID设备，将K-means算法，SVM算法和BP神经网络算法引入定位研究的计算当中，通过实验仿真，对比划分为2类，3类，4类宏区域所得出对应的均方根误差和误差累积分布函数，对定位区域划分为3类宏区域时，所得的均方根误差为0.9265m，其误差在1m以内的累积分布概率为67.2%.明显高于其它2类，达到了预期的实验目标.随后将本文算法和传统的BP神经网络定位算法进行比较，得出传统的BP神经网络算法的均方根误差为1.094m，通过比较可知，本文的算法明显优于传统的BP神经网络定位算法，对促进实用且低成本的无线定位系统具有较重要的理论意义和研究价值.