一种面向烟草行业的供给预测服务算法

洪 峰，潘法昱，赵建翊，高 楠，曹 斌，范 菁(浙江工业大学计算机科学与技术学院，杭州3003)

2(浙江省烟草公司宁波市公司，浙江宁波315000)

E-mail:hongfeng@zjut.edu.cn

1 引言

烟草行业一直以来是我国经济发展、财政收入的重要组成部分.烟草行业在坚持专卖制度的前提下，引入了市场竞争机制，形成市场和计划相结合的模式.现有烟草行业的销售和市场投放的服务模式是依靠自身经验和市场反馈的，但是这种模式需要依赖大量的人工参与［1］，从工作效率和准确率方面无法得到保证，进而不能很好解决区域性的烟草滞销、脱销等现实问题.事实上，面向烟草行业的销售和投放属于时间序列预测问题［2］，因此本文也将从时序预测出发展开研究.

解决烟草行业的时间序列问题主流的方法是统计方法和机器学习.统计方法如自回归滑动移动平均模型(ARIMA)［9，14］，一种利用拟合的 ARIMA 模型进行聚类的方式，进行时间序列预测，该方法聚类效果好，预测速度快，方法简洁易行，但是ARIMA模型只能利用一种特征进行时间预测，不能结合其他的特征数据，很难保证预测结果的准确性.在本文算法中结合了烟草销量数据在内的24维特征数据，给算法预测的准确性提供了保证.在机器学习领域，也有相关方法对上述烟草行业的销售投放预测问题进行过研究［10，12］.其中，一种基于神经网络算法的PSO-BP混合模型算法用来解决烟草供给预测，利用粒子群中粒子的位置表示神经网络中当前迭代次数中的权属集合，训练过程中产生的误差作为训练的适应度，但是往往建立模型时间复杂度高，可解释性差.还有例如李晓歌［3］，谢星峰［4］都提出过利用神经网络算法解决面向烟草行业的供给预测问题.虽然神经网络算法能很好地契合烟草数据的非线性特征，以及根据拟合结果进行供给预测，得到预测结果准确性较高.但是它是一个黑盒操作，无法表示输入数据与预测结果之间的关系;神经网络的结构难以确定(确定隐含层的节点数);节点数过多，容易使模型在训练中陷入局部极小值.现阶段还有类似于长短时记忆神经网络模型(LSTM)［20］的深度学习方法，但是此类方法的可解释性差，本文的算法可以清晰的了解到算法肌理.

综上考虑，我们提出了一种面向烟草行业的供给预测服务算法.以往算法都是利用回归的方式进行建模预测，而本文将回归的形式转变为用分类的方法去进行预测.该算法首先针对烟草销量数据进行预处理，包括去除异常值和数据合并.通过去异常值操作，保证算法的输入数据不会存在因为法定节假日和风俗习惯所引起的异常数据，以及数据合并过程中产生的异常数据.然后利用处理完的数据建立数据集，并取出预测时间历年前三个月的销量数据，训练随机森林模型，得出销量数据中每一维特征对于销量的重要程度指标，然后输入预测时间前一周的销量数据，得出下一周的预测销量.

同时在算法投放量预测模型中，采用比例的形式代替原有投放数量，具体为大类客户在全体客户投放量中所占比例，和在某一大类客户中，各个小类客户在该大类客户投放量中所占比例.取出预测时间之前各大类客户的比例数据，放入ARIMA模型进行训练，然后输入当前一周的比例数据，最终得出各个大类预测比例.接着利用在具体某一大类中，各个小类中所占该大类比例，最终得出各个小类在全体客户投放量中所占比例算法.通过上述步骤，从而完成整个烟草预测服务模型.

本文的主要贡献如下所示:

1)利用集成学习方法，避免在烟草数据的供给预测中会出现的过拟合现象;

2)在算法中加入了投放量预测模型，完善了供给服务，避免了现实中因投放不合理产生的滞销、脱销等问题出现;

3)首次采用了分类的方式，对烟草数据进行时间序列预测;

4)通过实验对本文算法进行验证，证明该算法能够保证较好的准确性.

2 预备知识

本节介绍了一系列重要的预备知识，以帮助理解本文算法.其中我们会讨论在销售预测模型中的随机森林算法，以及在投放预测模型中的ARIMA模型.

2.1 随机森林

随机森林算法广泛应用于分类，回归问题上，是一种集成学习方法［6，7］.顾名思义，随机森林算法可以分为概念，一个是“随机”，一个是“森林”.“随机”指的是在训练集中随机并且有放回的抽取训练样本.若不采用随机抽样，算法中每棵决策树的训练样本一样，那么最终训练出来的结果也是完全一样的，那么随机森林算法与普通决策树的算法并没有不同之处，同样，随机森林算法也包含了决策树算法的不足之处［8，11］，即过拟合，结果不稳定等问题.

此外，随机森林算法在训练样本抽取是有放回地抽样.因为训练样本仅仅只是通过随机抽取，而不采取放回的形式，那么每棵树的训练样本都是不同的，彼此之间没有交集，所以每棵树进行训练产生结果存在一定的差异.然而随机森林算法最后的结果是基于多棵树的训练结果，因此只是“片面地”采用不放回抽样，对于算法而言并没有益处.

“森林”的概念来源于集成学习方法，算法通过整合众多决策树，组成“森林”的形式，即将若干决策树训练结果进行投票，最终产生一个最好的训练结果作为算法输出.

简而言之:随机森林建立了多个决策树，并将它们合并在一起以获得更准确和稳定的预测.如图1所示，当我们需要预测一个特征为x的样本的值时，随机森林会将x输入到每一棵决策树中，每个决策树都会输出一个值.最后对所有值取平均作为随机森林的预测结果.

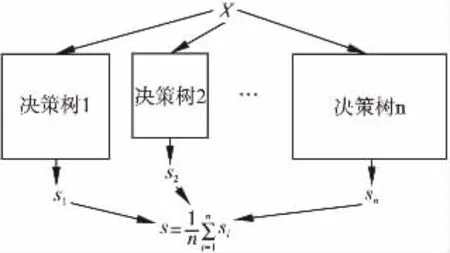
图1 随机森林模型示意图Fig.1 Random forest model diagram

2.2 ARIMA 模型

ARIMA 模型［9，14］，全程自回归积分滑动平均模型(Autoregressive Integrated Moving Average Model)，它包含三个部分，即AR(Auto Regression)自回归模型，I(Integration)单整数阶，以及MA(Moving Average)移动平均模型.

其中需要说明的是:1)AR描述的是时间序列在某一时刻的值与之前时刻的值之间的关系;2)I描述的是时间序列从非平稳序列经差分后转为平稳序列的计量模型;3)MA(Moving Average)模型描述的是时间序列在当前时刻与前一时刻之间的差值;4)ARIMA实际上是AR和MA模型的组合，它与ARMA模型的区别在于ARMA模型针对平稳时间序列建立的模型，而ARIMA模型则是针对非平稳时间序列建模.

因此，总的来说，ARIMA模型将预测对象随时间推移而形成的数据序列视为一个随机序列，然后按照下述3个步骤进行建模:1)将非平稳序列转化为平稳序列;2)确定模型的形式.即模型属于AR、MA、ARMA中的哪一种，这主要是通过模型识别来解决的;3)确定变量的滞后阶数.通过以上3个步骤，完成ARIMA模型的建模.

3 算法介绍

本文提出了一种准确高效的预测算法来预测烟草的销量和投放量.

如图2所示，算法主要可以分为3个步骤:1)历史数据预处理;2)建立销量预测模型;3)建立投放量预测模型.算法通过输入烟草数据，经预处理后，通过销量预测模型预测下一周的烟草销量.数据输入投放量预测模型中预测下一周各类客户的投放量.

在现实情况中，数据存在一定的滞后性(本文所用数据出现销售总量不等于投放量的情况)，故对于投放量预测模型中所用数据进行处理，把具体每类客户的投放量数值改为比例的形式进行替换，如小类客户在各自大类客户中所占比例，大类客户在全体客户中所占比例.然后把某一类客户的比例数据放入ARIMA模型中进行训练，最终预测下一周该类客户的比例.

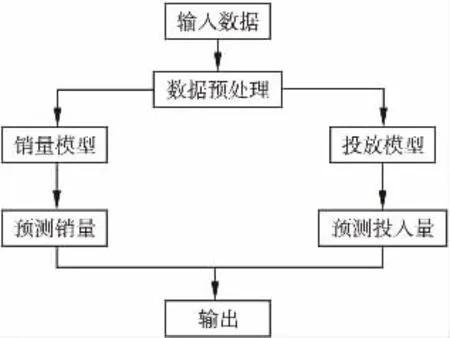
图2 算法流程示意图Fig.2 Algorithm process diagram

3.1 历史数据预处理

3.2 销量预测模型

测模型中所使用特征数据是经由烟草局专家挑选出的可能会影响烟草销量的特征.而上一步骤历史数据预处理中，对于销量数据中的特征数据进行删减，剔除异常数据，并经过数据合并，从而取得新的特征数据.因为本文需要对当前时间烟草销量进行预测，而无法获取当前时间的烟草的真实销量，考虑到烟草数据的季节性变化，本文利用当前时间的前三个月历史数据作为本文训练模型的训练集.

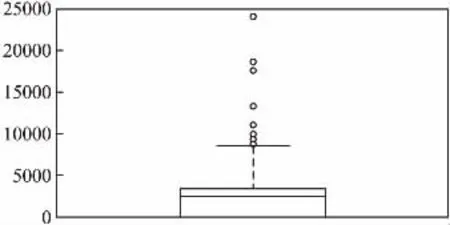
图3 日销量箱线图Fig.3 Daily sales boxplot diagram

主要思想:如图4所示，我们在数据库中取出2016、2017年近三个月的数据放入随机森林模型中进行指标重要程度训练，得出每一项指标重要程度之后保存该模型.然后在该模型中输入本周数据，经过该模型训练之后，最终得出下周预测销量.

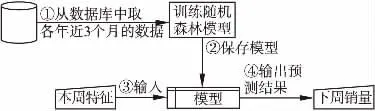
图4 销售模型建模示意图Fig.4 Modeling process for sales diagram

举例:假设当前时间为5月份，我们在数据库中取出2016、2017年近三个月(3月，4月，5月)的数据放入随机森林模型中进行指标重要程度训练，得出每一项特征的重要程度，并进行归一化处理，结果如表1中示例所示.

然后在模型中输入当前一周的数据，最终得出下周预测销量.

3.3 投放量预测模型

主要思想:如图5所示，ARIMA模型将预测对象随时间推移而形成的数据序列视为一个随机序列，然后按照下述3个步骤进行建模:1)平稳序列、纯随机序列检测;2)确定模型种类;通过模型识别来解决的;3)确定变量的滞后阶数，通过模型识别完成的.其中ARIMA模型识别可以通过自相关系数AC和偏相关系数PAC进行识别.

表1 特征重要程度归一化示例表Table 1 Feature importance normalization diagram

算法:通过绘制时间序列散点图判断该数据集是否平稳，如果平稳则不需要进行差分操作，ARIMA模型中参数d的值为0;如果不平稳则进行n阶差分操作，使之变成平稳序列，参数d的值就是对数据差分阶数n的值.

图5 投放模型建模示意图Fig.5 Modeling process for delivery diagram

对非纯随机序列做出acf图和pacf图，对图中数据的变化趋势进行判断，如果acf图出现拖尾，而pacf图出现p阶截尾的现象，则参数q为0，参数p为出现截尾时的阶数，即选用AR(p)模型;如果acf图出现q阶截尾的现象，而pacf图出现拖尾，则参数p为0，参数q为出现截尾时的阶数，即选用MA(q)模型;如果acf图出现拖尾，并且pacf图出现拖尾，则参数p、q为出现拖尾的阶数，即选用ARMA(p，q)模型.

在确定参数 p，d，q的值后，将数据送入 ARIMA(p，d，q)模型中进行训练.模型训练完成后即可直接输出下次的预测值.在所有大类占比预测完成之后进行放缩操作，方法为将每个大类的预测值除以所有大类预测值的和，保证所有放缩后大类预测值的和为1.

为了降低模型复杂度，并加快预测速度，将取出的前4周小类在大类中占比的数据按小类进行数据求平均值操作，得到每个小类在前4周的平均占比数据.最后将小类平均占比乘上对应大类占比的预测值就得到了下周小类占比的数据.

4 实验

本节将会通过一系列实验对于本文所提算法进行准确性评估，具体是针对烟草销量预测模型，投放量预测模型进行误差分析.

4.1 数据介绍

本文所使用数据来源于N市烟草局，数据具体可以分为两部分:1)2016年，2017年某一品牌的烟草销量数据;2)2016年，2017年各类经销商某一品牌烟草的投放量数据.

(4) B1中的成员均是Y中顶点色集合,因此，3,4,5,6中至少有3种色同时包含在每个C(ui)中,不妨设3,4,C(ui), i=1,2,…,10,从而每个C(ui)只能是以下集合之一:{1,3,4,5},{2,3,4,5},{1,3,4,5,6},{2,3,4,5,6},{1,2,3,4,5},{1,2,3,4,5,6},矛盾。

其中销量数据包含日销量在内专家选出的24维可能影响销量特征数据;投放量数据包含7个大类客户的投放数据以及各个大类客户中包含的小类客户共计21维投放量数据.

4.2 评估方法

针对本文算法得到预测结果，我们采用广泛使用的相对误差、最高误差、最低误差、平均误差来评估算法的准确性.相对误差是衡量算法准确率的重要指标，相对误差越低，表示算法的预测结果准确率越高.该组实验数据经实验产生最大的误差即最高误差，产生最小的误差即最低误差，所有数据的误差的平均值即平均误差，这三类误差都是基于相对误差实现的.相对误差计算公式具体如下:

4.3 销量预测模型

销售模型所使用的数据经预处理之后，考虑到季节性变化的情况，实验随机选取了 2017.3.27 ～ 4.2，2017.6.26 ～5.2，2017.9.11 ～9.17，2017.11.6 ～11.12 这四个星期进行预测.将星期前三个月作为训练集，对随机森林模型进行训练.例如2017.3.27 ～4.2，我们采用2016.1 到 2016.3.26 这三个月的数据作为训练集进行训练.

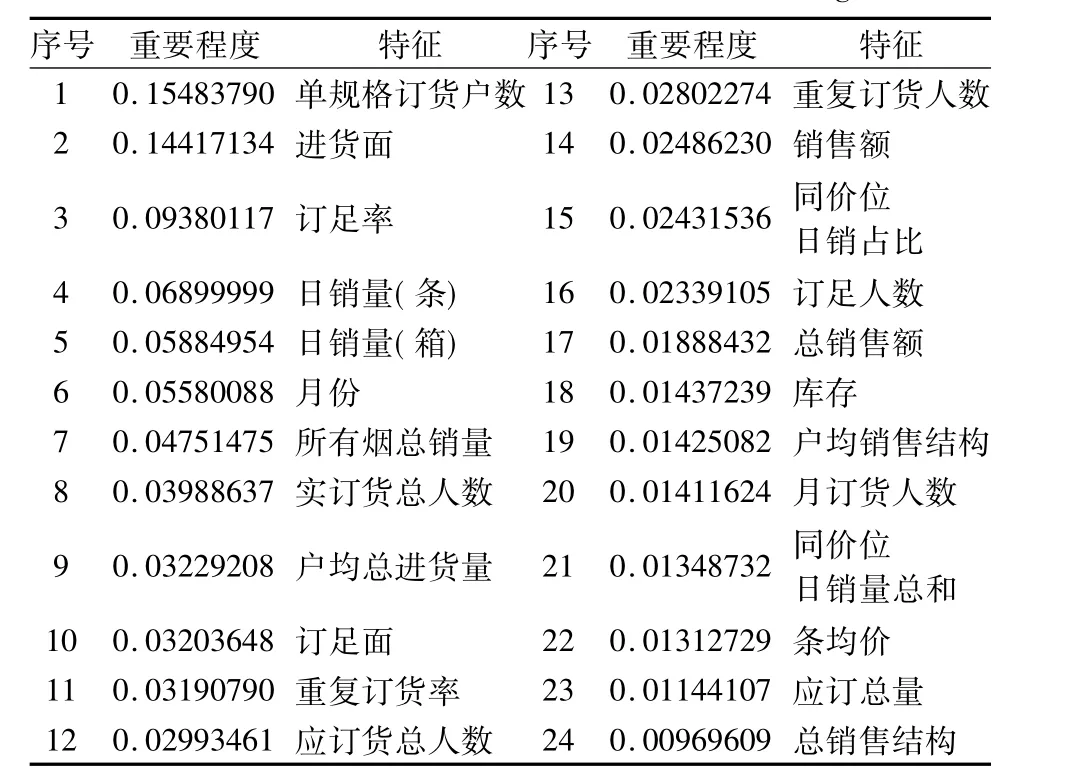
表2 销量特征归一化示意图Table 2 Sales characteristics normalization diagram

经模型训练，得出每一维特征对于烟草销量的重要程度指标，经归一化后，如表2所示.在该模型中输入预测时间前3个月的销量数据，最终得出预测结果，并与实际数据进行对比，结果如表3所示.

表3 销售模型预测结果示意图Table 3 Sales model forecast results diagram

表3中的差值为预测结果与实际数据的差值的绝对值.如表3所示，这四个星期的差值分别为57、70、81、86，他们的相对误差分别为 0.017、0.011、0.041、0.21，平均误差为0.076.实验证明该销售模型具有较好的预测准确性.

4.4 投放量预测模型

投放模型的数据为在2016年和2017年时间内向7个大类别的客户，共计21个小类别客户的产品投放量数据.实验选取第96周的投放量作为实验预测目的，并用第96周的真实投放量数据作为预测结果准确度衡量标准.

图6 A类客户数据散点图Fig.6 Class A customer data scatter diagram

以A类客户数据为例，首先取出A类客户投放量比例历史数据画出散点图，如图6所示，发现A类数据已经较为平稳，故选择不做差分处理，差分阶数d取0，再做出acf图(图7)和pacf图(图8)，从acf图中看出在2阶后有截拖尾现象，从pacf图中看出在2阶后有拖尾现象，得到p和q参数的值都为2，所以最终采用ARIMA(2，0，2)模型进行训练，训练完成之后输入A类客户前一周的数据，可以得到A类下一周的预测数据.

图7 A类客户自相关图Fig.7 Class A customer autocorrelation diagram

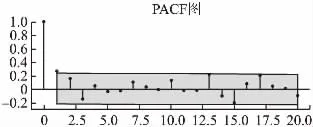
图8 A类客户的偏相关图Fig.8 Class A customer partial autocorrelation diagram

采用相同的方法对其他6个大类客户类进行建模和预测，最终得出各大类客户预测结果.将该预测结果与第96周的真实数据进行比较，得出如图9所示的箱线图.

图9 各大类客户预测结果箱线图Fig.9 Boxplot of forecast results for all major customers

从图中可以看到7个大类客户数据预测结果的最低误差在0.013左右，最高误差在0.15左右，大部分的误差范围在0.03到0.09的范围内，平均误差为 0.064，可见该模型具有较好的预测效果.

计算每个大类中小类的占比情况.这里不再使用ARIMA模型，实验计算一个大类中各个小类在该大类中的占比，然后利用平均值作为每个大类中各个小类所占比例情况的预测值.然后该预测值和大类在全体客户中的所占比例得出小类客户在全体客户中所占比例情况.如图10所示.

图10 各小类客户预测结果箱线图Fig.10 Each class customer forecast results boxplot

从图中可以看到各小类客户在全体客户中所占比例最高误差为0.16左右，最低误差为0.015左右，大部分的误差范围在0.025到0.095之间，整体的平均误差为0.068，针对小类客户的预测也具有较好的效果.

此外，实验尝试直接对小类客户数据进行ARIMA模型建模.而实验结果一方面模型数量大大增加，时间耗费和计算量大大增加，而且预测结果的平均相对误差达到30%.

5 相关工作

面向烟草行业的供给预测问题本质上就是一个时间序列预测问题［13］，然而由于供给预测中烟草销量数据具有短期性，季节性，非线性等特点，该问题的解决需要更加针对性的预测方法.为此国内许多学者在该问题上做了许多工作.

一般在烟草行业内进行时间序列预测的方法主要可以分为两类:单模型和混合模型.单模型即利用一个模型实现时间序列预测的功能.例如陈日进［15］使用传统时间序列预测法中的一次指数平滑预测法对于烟草销量进行预测，该方法适用于较为平稳以及变化趋势不明显的烟草数据其中平滑系数的取值对于销量预测结果有较大影响，平滑系数取值也需要多次进行测试才能保证销量预测结果的误差较低.还有例如基于灰色预测模型的灰色预测法［16］，该方法是通过给予的烟草销量数据，建立数学模型，并根据该模型对烟草销量进行预测.但是该方法在波动变化明显的数据中，预测结果误差往往较大.刘璐等人［5］利用SVM(支持向量机，Support Vector Machine)解决面向烟草行业的供给预测问题.虽然SVM可以解决部分烟草数据量较小的问题，而且也能避免上述神经网络结果选择和局部极小点问题，但是SVM对于参数调节和函数的选择十分敏感，容易引起预测结果的不准确.

混合模型即利用几种模型进行混合实现时间预测的目的.目前在混合模型中主流的还是基于机器学习的混合模型.例如靳志伟［17］提出了基于BP神经网络的烟草预测PSO-BP混合算法，利用粒子群中粒子的位置表示神经网络中当前迭代次数中的权属集合，训练过程中产生的误差作为训练的适应度，但是往往建立模型时间复杂度高，可解释性差.罗艳辉等人［18］提出了基于ARMA的混合算法，利用PERT模型和ARMA模型针对烟草时间序列进行预测，得到的预测值以一定的权值比例相加得到最终的预测结果.该方法加入了一定的人为判断，只能处理较小的数据，在大数据量的操作中预测结果不会很好.罗彪等人［19］将传统的节假日设为虚拟变量，构建基于时间序列分解和虚拟变量的改进模型，在现实操作中预测结果不太理想.

6 总结和展望

本篇文章提出一种面向烟草行业供给预测服务.算法利用随机森林模型，得出数据中每一维特征数据的重要程度，利用当前时间的数据作为输入得出下一周销量的预测;化大类客户和小类客户数据为比例的形式，利用ARIMA模型对它们进行预测.最后本文通过实验比较，证明了算法得到的预测结果与真实数据的准确性较高，能够销量平均误差为0.076，大类客户投放量平均误差为0.13，小类客户投放量平均误差0.068.

本文后续工作将从以下几个方面展开:

1)增加对于时间序列验证过程，保证其准确率;

2)对于算法的公平性进行进一步的讨论.