基于最小二乘支持向量机对称性的混沌时间序列预测

陈佳 郑恩让 贺永宁

摘  要： 利用最小二乘支持向量机的对称性约束条件挖掘混沌时间序列的对称性，分析混沌系统固有的对称特性，提出一种对称性最小二乘支持向量机的混沌时间序列预测方法。该方法将混沌系统的对称性作为先验知识嵌入预测模型，Lorenz系统的仿真结果表明该方法不仅能够精确地预测混沌时间序列，而且扩展了混沌系统的预测空间，这一结论预示着最小二乘支持向量机是一种研究混沌时间序列的有效方法。

关键词： 混沌时间序列预测; 支持向量机; 最小二乘法; 对称性分析; 混沌系统; Lorenz 系统

中图分类号： TN911.1?34                        文献标识码： A                         文章编号： 1004?373X（2019）15?0109?04

Chaotic time series prediction based on symmetry of LS support vector machines

CHEN Jia1， ZHENG Enrang1， HE Yongning2

（1.Shannxi University of Science and Technology， Xian 710046， China;

2. Xian Jiaotong University， Xian ，710049， China）

Abstact：The symmetry of the chaotic time series is mined and the inherent symmetry characteristic of the chaotic system is analyzed by means of symmetry constraints of least square support vector machines.，The forecasting method of chaotic time series using the least square support vector machines with symmetry is proposed， which takes the symmetry of chaotic system as priori knowledge to embed it into the prediction model. The simulation result of Lorenz system shows that the proposed method can predict the chaotic time series accurately， and expand the forecast room of the chaotic system. This conclusion implies that the least square support vector machine is an effective tool to study chaotic time series.

Keywords：chaotic times series prediction; support vector machine; least square method; symmetry analysis; chaotic system ;Lorenz system

0  引  言

近年來，对非线性系统尤其是混沌时间序列预测已经成为非常重要的研究方向之一，并已在地质科学、水文预报、军事科学、空间科学、气象预报、工业自动化、信号处理等领域中得到了广泛的应用。在混沌时间序列分析中建立一个基于训练集学习，并能够准确预测未来数据的非线性“黑盒子”预测模型是一项具有挑战性的任务[1?7]。通常时间序列模型基于已有[t]时刻的数据，而最终评估模型的数据仿真验证是从[t+1]时刻开始。混沌系统吸引子的局部不稳定性导致时间序列不仅呈现出非线性行为特性，而且也呈现大范围的突变，因此，混沌系统产生时间序列的本质决定了混沌时间序列的预测是一项非常困难的工作。如果混沌时间序列建模时充分利用其固有的某些特征如对称性，则混沌时间序列的模型精度和建模能力将进一步提升[8?12]。

本文挖掘混沌时间序列的对称性，利用最小二乘支持向量机（Least Squares Support Vector Machines，LS?SVM）的对称性约束条件，分析混沌系统固有的对称特性，提出一种对称性最小二乘支持向量机的混沌时间序列预测方法，将对称性作为混沌系统的先验信息应用到混沌时间序列建模中，并以Lorenz系统为例对对称性最小二乘支持向量机的混沌时间序列预测方法进行验证，仿真结果表明该预测方法不仅提高了混沌时间序列建模的精度，而且扩展了混沌模型的预测空间。

1  最小二乘支持向量机的对称性分析

若时间序列数据样本集为[{xk，yk}Nk=1]，[xk∈Rm]，[yk∈R]，则支持向量机的拟合函数形式为[13]：

式中：[ω]为权向量;[b]为偏差;[?（x）]为把输入空间映射到一个高维特征空间中的非线性映射函数;[ek]为假定服从零均值，某一固定偏差分布。因为[?（x）]可用核函数代替，而核函数可用原空间函数实现，因而无需知道其具体形式。LS?SVM是基于正则化理论对经典支持向量机的改进[14]，这样在很大程度上简化了支持向量机的求解，也是支持向量机在二次损失函数下的一种形式，并用等式约束条件替代支持向量机的不等式约束条件，通过求解一系列线性方程组来替代传统支持向量回归中的二次型规划问题，这在实际应用中表现出运算简捷、收敛快和精度高的优点。拟合函数中最优权向量[ω]和偏差[b]可通过最小化拟合误差的平方和及正则化项组成的目标函数获得：

式中：正实数[γ]是调节常数，这样可在训练误差和模型复杂度间取折衷以便使所求函数具有好的泛化能力，且[γ]值越大，模型预测误差越小;[s]取值1或-1，依赖于对称类型。第一个约束条件为LS?SVM的标准约束条件，第二个约束条件是通过赋值[s]取值1或-1，赋予非线性映射函数[?（x）]的奇偶特性。如果核函数满足[k（xk，-xi）= k（-xk，xi）]，因为[ω]维数可能为无限值故难以最小化式（2），但可在对偶空间上求取[ω]，建立Lagrangian方程：

式（8）为等效的容纳非线性特性的对称核函数。需要强调的是，式（8）与式（7）中矩阵的维数并没有发生改变，因此第二个限制条件并没有增加问题求解的难度，仅仅是把新问题转化成了核函数。分析式（8），不难发现高斯核函数、小波核函数等均可以组成对称核函数[15]。

2  混沌系统的对称性分析

许多混沌系统具有对称性导致其混沌吸引子也具有某种对称性，混沌系统的对称吸引子特性已经被多位学者深入研究，典型的对称混沌系统如[Z4]对称因子混沌系统，[λ=]0.16，[μ=]0.74，时间步长为0.01时，20 000个数据点的[（x，y）]和[（x，ω）]映射关系分别如图1a），图1b）所示，该混沌系统的映射关系无论是[（x，y）]还是[（x，ω）]均具有对称性;100 000 000个数据点的[（x，y）]映射关系如图1c）所示，不难发现随着数据点的大量增加混沌系统仍然呈现对称性。

图1  [λ=]0.16，[μ=]0.74，时间步长为0.01的映射关系图

3  预测实例

实践研究表明，基于LS?SVM对称性的混沌时间序列预测方法由于其将混沌时间序列的对称性作为先验知识，因而在复杂非线性建模中具有更加独特的优越性。对初始状态极其敏感是混沌时间序列的显著特征之一，导致混沌时间序列预测非常困难。但是实验结果表明，LS?SVM能够在一定时间内比较精确地预测未来混沌时间序列。为衡量预测模型的精确性，采用相对误差：

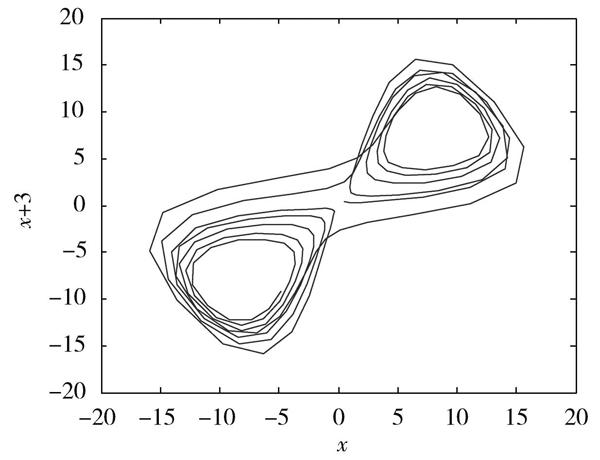
假定初始条件[x0=5]，[y0=5]，[z0=15]，利用四阶五级Runge?Kutta算法求解Lorenz系统的数值解，取采样间隔时间为0.05 s，相空间如图2a）所示，不难看出，Lorenz系统的[x?y?z]相空间图呈现明显的对称性。关于[x]的时间序列如图2b）所示，其时间序列具有复杂的非线性混沌特征，而且时间序列呈现高度的自相关性，直接建立其预测模型存在很大的困难。

利用前[N=]200个时间序列作为训练集（如图3所示），取嵌入维数[m]为3、延迟时间[τ]为2，在[{γ，α，s}=]{30，2.5，-1}时进行训练建立预测模型。

为了验证模型的准确性，对将来的200个数据点进行验证，所建混沌时间序列预测模型的预测值与混沌时间序列实际值的比较曲线如图4所示，实线为实际混沌时间序列，点为预测值，不难看出基于LS?SVM的对称性，将混沌系统的对称性作为先验知识嵌入预测模型中能够进一步更加精确地预测未来的混沌时间序列。

图2  Lorenz混沌时间序列

图3  Lorenz时间序列训练数据

圖4  预测值与实际值比较曲线

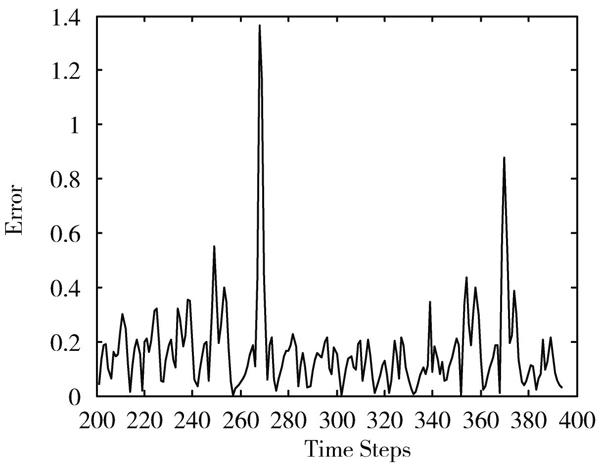
为了进一步比较预测性能，预测值与实测值的预测误差曲线如图5所示，除个别点外大部分预测误差小于0.5，RMSE误差为0.025 1，这个预测精度对于介于随机和规律之间的混沌时间序列预测来说是非常高的。

图5  预测误差曲线

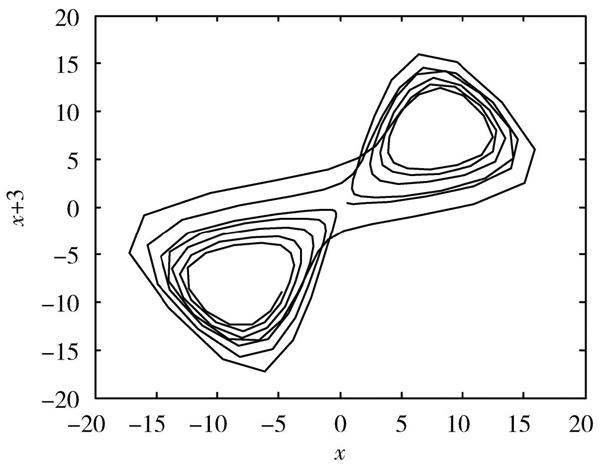
利用预测的时间序列重构的曲线如图6所示。不难看出该模型的预测值与系统的实际值吻合得比较好，这说明该方法能够从无序和复杂中产生出有序和规律的系统挖掘混沌时间序列的对称性等有序行为，并能够精确预测其未来的混沌时间序列。

图6  预测的时间序列重构曲线

4  结  语

本文利用最小二乘支持向量机的对称性约束条件挖掘混沌时间序列的对称性，分析了混沌系统固有的对称特性，提出一种对称性最小二乘支持向量机的混沌时间序列预测方法，以Lorenz系统为例对对称性最小二乘支持向量机的混沌时间序列预测方法进行验证，仿真结果表明该预测方法不仅提高了混沌时间序列建模的精度，而且扩展了模型的预测空间。

参考文献

[1] WEIGEND A S， GERSHENFELD N A. Time series prediction forecasting the future and understanding the past [M]. New Jersey： Addison?Wesley， 1993.

[2] 陈佳，郑恩让，崔万照，等.基于小波支持向量回归的电力系统负荷预测[J].现代电子技术，2009，32（16）：135?139.

CHEN Jia， ZHENG Enrang， CUI Wanzhao， et al. Power load foresting based on wavelet support vector regression [J]. Modern electronics technique， 2009， 32（16）： 135?139.

[3] CUI Wanzhao， ZHU Changchun， BAO Wenxing， et al. Prediction of the chaotic time series using support vector machines [J]. Acta physica sinica， 2004， 53（10）： 3303?3310.

[4] CUI Wanzhao， ZHU Changchun， BAO Wenxing， et al. Prediction of the chaotic time series using support vector machines for fuzzy rule?based modeling [J]. Acta physica sinica， 2005， 54（7）： 3009?3018.

[5] SHEN Lihua， CHEN Jihong， ZENG Zhigang， et al. Chaotic time series prediction based on robust extreme learning machine[J]. Acta physica sinica， 2018， 67（3）： 030501.

[6] 顾兆军，李冰，刘涛. 基于PSO?Elman模型的网络流量预测[J].现代电子技术，2019，42（1）：82?86.

GU Zhaojun， LI Bing， LIU Tao. Network traffic prediction based on PSO?Elman model [J]. Modern electronics technique， 2019， 42（1）： 82?86.

[7] 姜娇娇，郭俊，杨淑莹. 基于粒子滤波的混沌时间序列局域多步预测[J].现代电子技术，2018，41（1）：43?46.

JIANG Jiaojiao， GUO Jun， YANG Shuying. Particle filtering based local multi?step prediction for chaotic time series [J]. Modern electronics technique， 2018， 41（1）： 43?46.

[8] AGUIRRE L A， LOPES R， AMARAL G， et al. Constraining the topology of neural networks to ensure dynamics with symmetry properties [J]. Physical Review E， 2004， 69： 026701.

[9] YU Jinjiang， ZHANG Mingxuan， XU Haibo. Nonlinear dyna?mics and control of symmetric chaotic systems [J]. Acta physica sinica， 2004， 53（11）： 3701?3705.

[10] ABREU S， ASTON P ， MELBOURNE I. Symmetric chaos in a local codimension two bifurcation with the symmetry group of a square [J]. SIAM journal on. applied dynamical systems， 2005， 4（1）： 32?52.

[11] KING G P， STEWART I N. Symmetric chaos， in nonlinear equations in the applied sciences [M]. New York： Academic Press， 1991： 257?315.

[12] FIELD MJ.， Lectures on bifurcations， dynamics and symmetry [M]. Harlow： Longman， 1996.

[13] VAPNIK V N. The nature of statistical learning theory [M]. New York： Springer， 1995.

[14] SUYKENS J A K， VAN GESTEL T， DE BRABANTER J， et al. Least squares support vector machines [M]. Singapore： World Scientific， 2002.

[15] STEWART I. The Lorenz attractor exists [J]. Nature， 2000， 406： 948?949.

[16] FELLMAN J. Transfer policies with discontinuous Lorenz curves [J]. Journal of mathematical finance， 2016， 6： 28?33.