广义正交模糊Maclaurin对称平均算子及其应用*

王 军，张润彤+，朱晓敏

1.北京交通大学 经济管理学院，北京 100044

2.北京交通大学 机械与电子控制工程学院，北京 100044

1 引言

多属性决策是现代决策科学的一个重要分支。由于决策问题的复杂性，如何在复杂和不确定性环境下表示属性值，是需要重点考虑的问题。Zadeh[1]提出的模糊集是一种描述不确定现象的有效工具。随后，学者Atanassov[2]对模糊集理论进行了扩展，提出了直觉模糊集理论。由于直觉模糊集同时具备隶属度和非隶属度两个维度，因而在描述不确定信息和现象时比经典模糊集更有效。由于直觉模糊集的这一特点，在过去的几十年里直觉模糊集被广泛应用在疾病诊断[3]、模式识别[4]、聚类分析[5]以及多属性决策问题中[6-7]。直觉模糊集需要满足的约束条件是隶属度和非隶属度之和小于或等于1。这样的约束条件使得直觉模糊集的应用受到了很大的约束，因而限制了其使用范围。因此，学者Yager[8]对直觉模糊集理论进行了扩充，提出了毕达哥拉斯模糊集理论。

毕达哥拉斯模糊集的约束条件是隶属度和非隶属的平方和不大于1。由此可见，毕达哥拉斯模糊集比直觉模糊集所能描述的范围更广。此后，许多学者将研究重点放在基于毕达哥拉斯模糊集的多属性决策问题上。例如，文献[9]提出了毕达哥拉斯模糊软集的概念，并将这一模糊集应用到多属性决策问题中。为了消除专家过高或者过低决策值给决策结果带来负面的影响，文献[10-11]提出了一些毕达哥拉斯模糊幂加权平均算子，并基于这些算子提出了一种解决多属性决策问题的算法。文献[12-13]考虑毕达哥拉斯模糊集中隶属度和非隶属度之间的交叉关系，提出了几类毕达哥拉斯模糊交叉集成算子。为了捕获毕达哥拉斯模糊数之间的相关关系，Liang等[14]提出了一些毕达哥拉斯模糊Bonferroni平均算子。Garg[15]提出了一种解决区间值毕达哥拉斯模糊多属性决策问题的线性回归方法。文献[16]提出了一系列广义毕达哥拉斯模糊Bonferroni平均算子。Li等[17]提出了一系列毕达哥拉斯模糊幂Muirhead平均算子。受到犹豫模糊集的启发，Garg[18]提出了犹豫毕达哥拉斯模糊集，并将其应用在多属性决策问题中。Xing等[19]基于Frank范数提出了一系列的毕达哥拉斯Choquet积分算子。Tang和Wei[20]研究了毕达哥拉斯二元语言集及其集结算子，并提出了一种新的多属性决策方法。为了处理毕达哥拉斯隶属度和非隶属之间的交叉关系，并且能够捕获多个毕达哥拉斯模数之间的相关关系，Xu等[21]提出了同一系列毕达哥拉斯模糊交叉Muirhead平均算子。

然而，毕达哥拉斯模糊集在描述不确定性和模糊性时仍存在着局限。例如当某位专家分别用0.7和0.8代表其决策意见的隶属度和非隶属度时，由于0.72+0.82=1.13＞1，因此专家的决策意见（0.7，0.8）并不能用毕达哥拉斯模糊集表示。为解决这类问题，学者Yager[22]提出了广义正交模糊集。广义正交模糊集的约束条件是隶属度和非隶属度的q次方之和小于或者等于1(q≥1)。随后文献[23]提出了一系列广义正交模糊加权算术平均和加权几何平均算子。文献[24]提出了一簇广义正交模糊Bonferroni平均算子。Wei等[25]提出了一系列广义正交Heronian平均算子。然而现有的广义正交模糊集结算子只能考虑两个变量之间的相关关系。为了捕获多个输入变量之间的相关关系，本文利用Maclaurin对称平均算子[26]集结广义正交模糊信息，提出一系列广义正交模糊Maclaurin对称平均算子，并将这些算子应用在多属性决策问题中。

2 预备知识

2.1 广义正交模糊集

定义1[22]设X为一个非空一般集合，则定义在X上的广义正交模糊集A的表达式为：

其中，uA(x)和vA(x)分别表述元素x属于集合X的隶属度和非隶属度，并且满足 0≤uA(x)≤1，0≤vA(x)≤1以及 0≤uA(x)q+vA(x)q≤1(q≥1)。为了方便，记α=(u,v)为一个广义正交模糊数。显然，广义正交模糊数的隶属度空间比毕达哥拉斯和直觉模糊的隶属度空间都大，如图1所示。

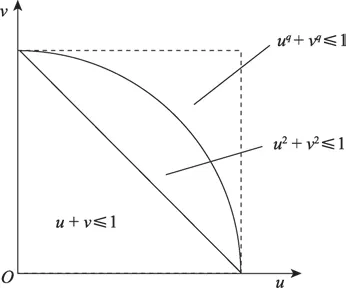
Fig.1 Space of membership degree ranges of different fuzzy sets图1 各模糊集的隶属度空间范围

定义2[23]设α1=(u1,v1)和α2=(u2,v2)为两个广义正交模糊数，并且λ为任意正数，则广义正交模糊数的运算法则为：

定义3[23]设α=(u,v)为一个广义正交模糊数，则α的得分函数定义为S(α)=uq-vq，α的精确函数定义为H(α)=uq+vq。对于任意两个广义正交模糊数α1=(u1,v1)和α2=(u2,v2)，则有：

（1）若S(α1)＞S(α2)，则α1＞α2。

（2）若S(α1)=S(α2)，则：

若H(α1)＞H(α2)，则α1＞α2；

若H(α1)=H(α2)，则α1=α2。

2.2 Maclaurin对称平均算子

Maclaurin对称平均算子是一种有效的信息集成算子，最初被广泛应用在实数领域。近几年来，Maclaurin对称平均算子在模糊信息集成领域也得到了广泛的应用。Maclaurin对称平均算子的优势是能够反映多个输入变量之间的相关关系。

定义4[26]设aj(j=1,2,…,n)为一系列非负实数，并且k=1,2,…,n，若：

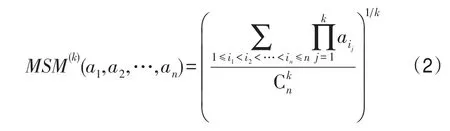
则称MSM(k)为Maclaurin对称平均（Maclaurin symmetric mean，MSM）算子，其中 (i1,i2,…,ik)遍历了(1,2,…,n)的所有k元组合，是二项式系数。

另外可以证明MSM算子满足幂等性、单调性及有界性[26]。

3 广义正交模糊集结算子

利用MSM算子集成广义正交模糊信息，提出了一系列广义正交模糊Maclaurin对称平均算子。

3.1 广义正交模糊Maclaurin对称平均算子

定义5设αi=(ui,vi)(i=1,2,…,n)为一组广义正交模糊数，并且k=1,2,…,n。若：

则称q-ROFMSM(k)为广义正交模糊Maclaurin对称平均（q-rung orthopair fuzzy Maclaurin symmetric mean，q-ROFMSM）算子，其中(i1,i2,…,ik)遍历了(1,2,…,n)的所有k元组合，Ckn是二项式系数。

定义5给出了MSM算子在广义正交模糊环境下的数学表达式。通过定义5可以看到，MSM在广义正交模糊环境下的数学表达形式与在实数环境下的数学表达形式是类似的。需要指出的是，在实数环境下的MSM算子遵循实数的运算法则，在广义正交模糊环境下的MSM算子需要遵循广义正交模糊集的运算法则（即定义2）。根据定义2和定义5可以得到如下定理。

定理1设αi=(ui,vi)(i=1,2,…,n)为一组广义正交模糊数，并且k=1,2,…,n，则利用q-ROFMSM算子集结后的结果仍然是广义正交模糊数，且：

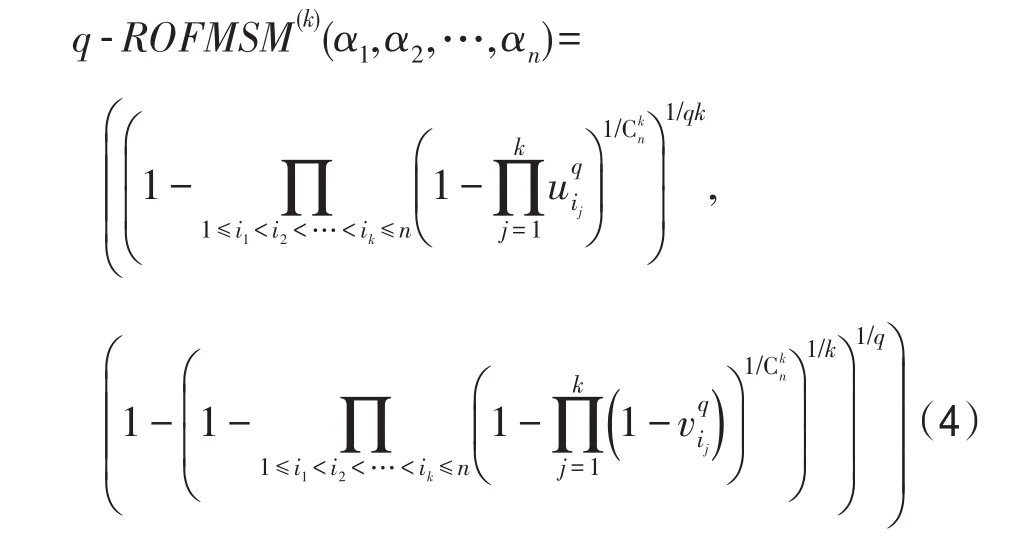
证明首先证明等式（4）的正确性，再证明集结结果仍然为广义正交模糊数。根据定义2，可以得到：

故算子的集结结果也是一个广义正交模糊数。□

此外q-ROFMSM算子具有如下性质。

性质1（幂等性） 设αi=(ui,vi)(i=1,2,…,n)为一组广义正交模糊数，若任意αi满足αi=α=(u,v)，则有：

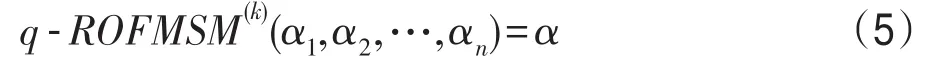
证明由于αi=α=(u,v)对于所有i都成立，根据定理1可得：

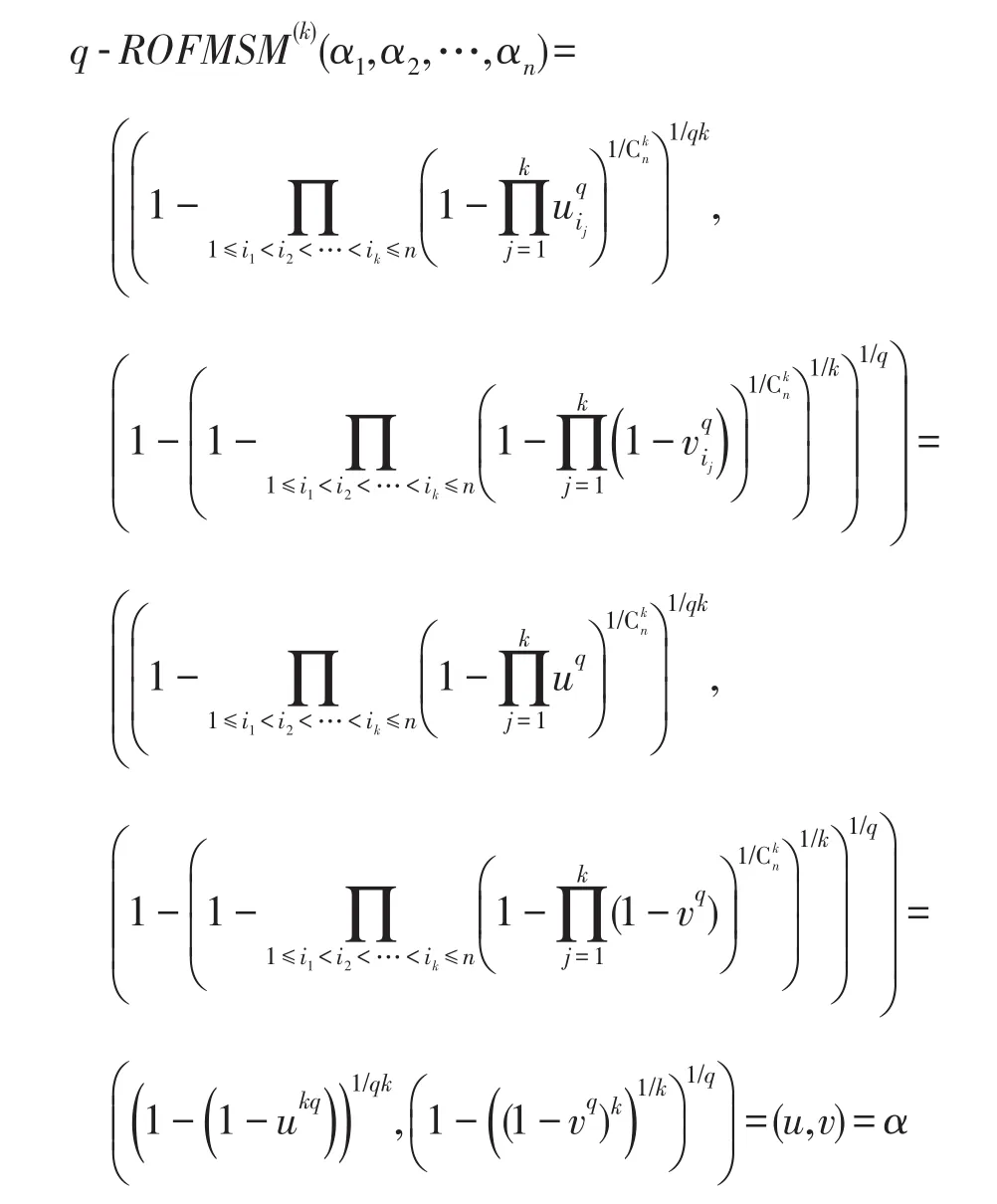
即等式成立，q-ROFMSM算子具有幂等性。

性质2（单调性） 令αi=(ui,vi)和βi=(si,ti)(i=1,2,…,n)为两组广义正交模糊数，若ui≤si，vi≥ti对于任意i都成立，则有：

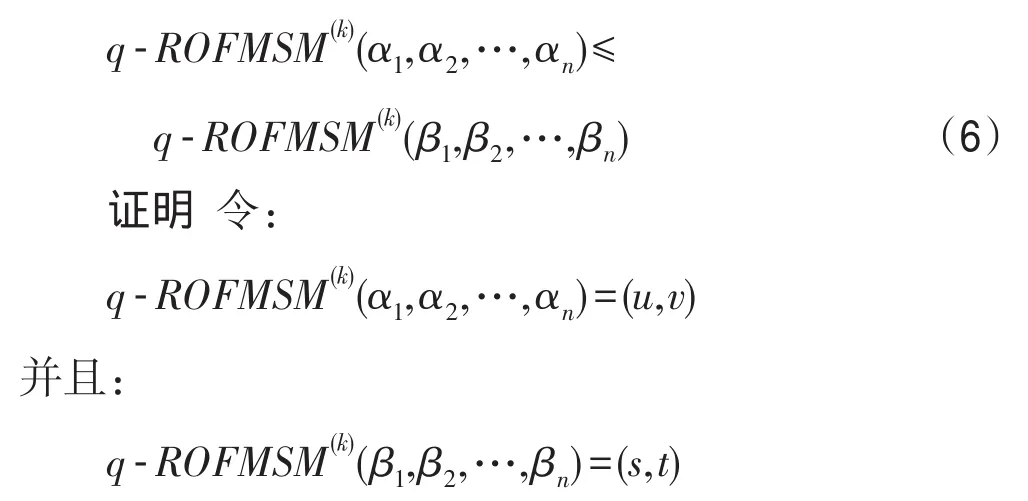
由于ui≤si对于所有i都成立，则有：

即u≤s。同理可得v≤t。根据定义3，两个广义正交模糊数(u,v)和(s,t)之间的大小关系是(u,v)≤(s,t)，即：

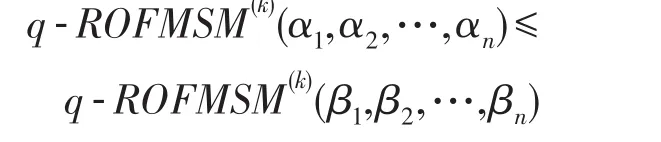
性质3（有界性） 设αi=(ui,vi)(i=1,2,…,n)为一组广义正交模糊数，则有：

其中：

此时q-ROFMSM算子退化为广义正交模糊平均算子[23]。

情形2当k=2时，则有：

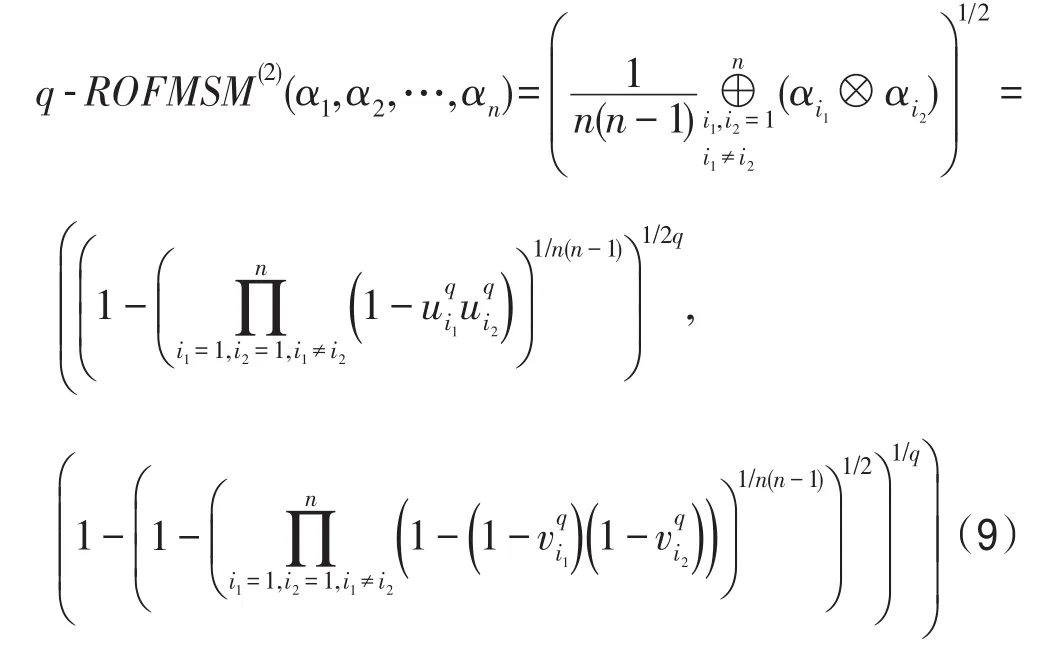
此时q-ROFMSM算子退化为广义正交模糊Bonferroni平均算子[24]。

情形3当k=3时，则有：

此时q-ROFMSM算子退化为广义正交模糊广义Bonferroni平均算子。

情形4当k=n时，则有：

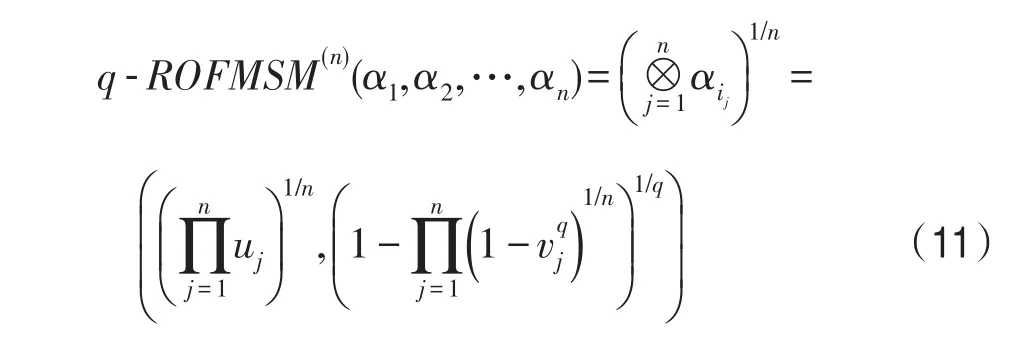
此时q-ROFMSM算子退化为广义正交模糊几何算子[23]。

情形5当q=1时，则有：

此时q-ROFMSM算子退化为直觉模糊Maclaurin对称平均算子[27]。

情形6当q=2时，则有：

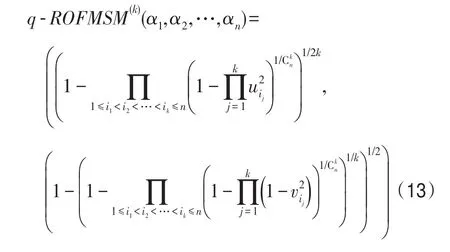
此时q-ROFMSM算子退化为毕达哥拉斯模糊Maclaurin对称平均算子[28]。

3.2 广义正交模糊加权Maclaurin对称平均算子

考虑到在实际的决策问题中，输入变量往往具有不同的重要程度，定义广义正交模糊加权Maclaurin对称平均（q-rung orthopair fuzzy weighted Maclaurin symmetric mean，q-ROFWMSM）算子。

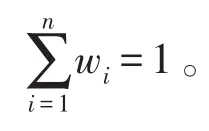
则称q-ROFWMSM(k)为q-ROFWMSM算子，其中(i1,i2,…,ik)遍历了(1,2,…,n)的所有k元组合，Ckn是二项式系数。

定理2令αi=(ui,vi)(i=1,2,…,n)为一组广义正交模糊数，并且k=1,2,…,n。则利用q-ROFWMSM算子集结的结果仍为广义正交模糊数，并且：

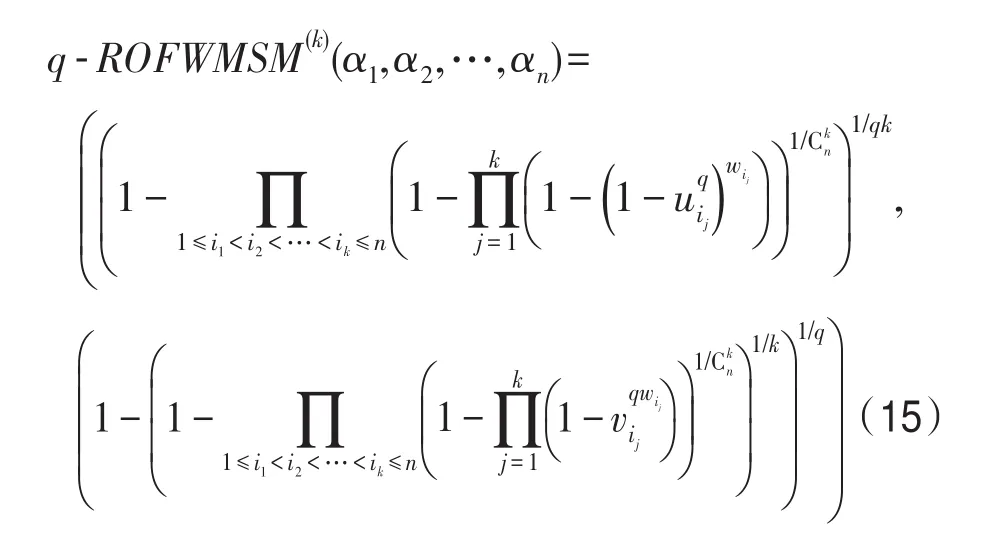
定理2的证明过程与定理1的证明过程类似。此外q-ROFWMSM算子具有如下性质。

性质1（单调性） 令αi=(ui,vi)和βi=(si,ti)(i=1,2,…,n)为两组广义正交模糊数，若ui≤si，vi≥ti对于任意i都成立，则有：

性质2（有界性） 设αi=(ui,vi)(i=1,2,…,n)为一组广义正交模糊数，则有：

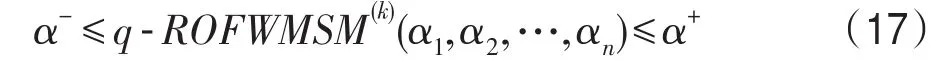
其中：

上述两个性质的证明过程与q-ROFMSM算子性质的证明过程类似，这里不再赘述。

4 基于广义正交模糊Maclaurin对称平均算子的多属性决策方法

步骤1标准化决策矩阵。在实际的多属性决策问题中，属性往往包含两种类型，即效益型属性和成本型属性。因此需要根据以下公式对原决策矩阵进行标准化。

其中，I1和I2分别表示效益型属性和成本型属性。

步骤2利用广义正交模糊加权Maclaurin对称平均（q-ROFWMSM）算子集结专家意见，即：

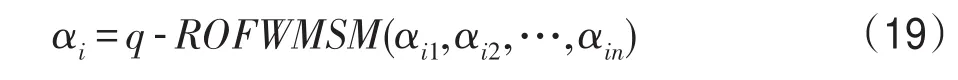
进而得到每个选项的综合属性值。

步骤3根据定义计算每个选项的综合属性值的得分函数并将候选项x={x1,x2,…,xm}降序排列。

步骤4根据排序结果选择最优方案。

5 应用实例

为提高企业的竞争优势，某公司决定开展一项新的业务[29]。经过初步的调研，企业领导层决定从5个可能方案中选择一个最优的方案。这5个可能的方案记作{x1,x2,x3,x4,x5}。为了选择最优选项，该企业组织专家对5个备选方案进行严格的评审。对所有备选方案的评审主要包括4个方面，即竞争优势（G1）、发展潜力（G2）、环境友好性（G3）以及社会影响力（G4）。属性的权值向量为w=(0.2,0.1,0.3,0.4)T。专家利用直觉模糊数对备选方案的属性进行评价，进而得到一个如表1中的直觉模糊决策矩阵。

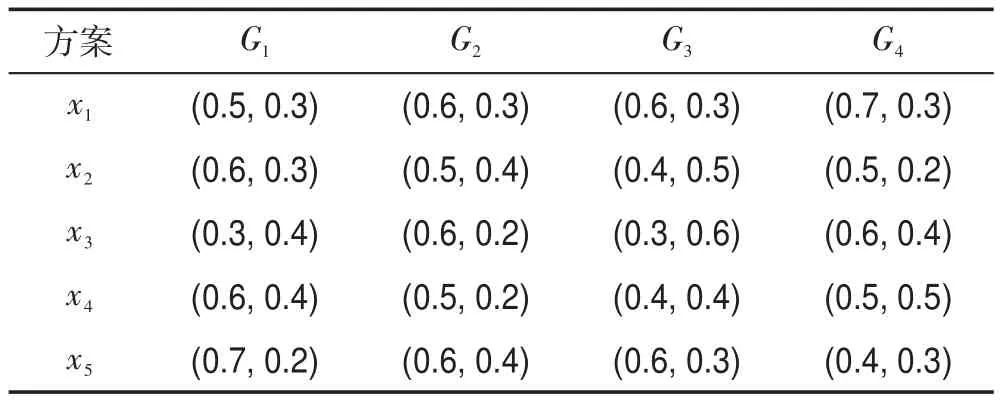
Table 1 Intuitionistic fuzzy decision matrix表1 直觉模糊决策矩阵

5.1 决策过程

步骤1由于所有的属性均为效应型属性，因此决策矩阵不需要标准化。

步骤2利用广义正交模糊加权Maclaurin对称平均算子集结决策矩阵（令k=2,q=3），可以得到候选方案的综合属性值。即：

步骤3计算综合值的得分函数，可以得到：

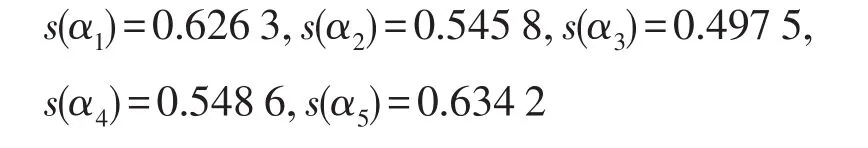
方案的排序结果为x5≻x1≻x4≻x2≻x3。

步骤4根据排序结果可知最优方案为x5。

5.2 参数对排序结果和最优选项的影响

广义正交模糊加权Maclaurin对称平均算子中有两个重要的参数k和q。显然参数k和q在算子的集结结果和排序结果中扮演着重要角色。赋予参数不同值，则可以得到不同的得分函数和排序结果。在广义正交模糊加权Maclaurin对称平均算子中赋予参数k不同的值时，其得分函数和排序结果如表2所示。为了不失一般性，令q=3。

从表2中可以看出，广义正交模糊加权Maclaurin对称平均算子中的参数k取不同值时，得分函数及排序结果均不同。当k=1,2,3时，最优方案均为x5。当k=4时，最优方案为x1。另外，随着k值的增大，方案的得分函数不断变小。即得分函数随k值单调递减。因此参数k的值可以视为是决策者对决策方案的乐观或者悲观的程度。即当决策者对决策方案比较悲观时，可以尽可能地给广义正交模糊加权Maclaurin对称平均算子中的参数k赋予一个较大的值；反之当决策者对决策方案比较乐观时，尽可能给参数k赋较小值。

此外参数q的取值对结果的影响很大。参数q本质上指的是决策者评价结果的信息范围。给广义正交模糊加权Maclaurin对称平均算子中的参数q赋予不同的值，则得分函数和排序结果如图2所示。为了不失一般性，令k=2。

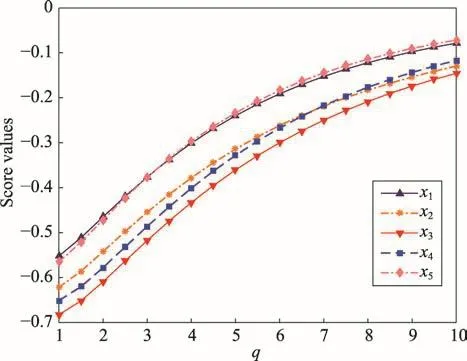
Fig.2 Decision results by q-ROFWMSM operator with respect toq(k=2)图2 q-ROFWMSM算子随q变化的决策结果(k=2)

从图2中可以看出，随着q的增大，即决策者信息范围越大，方案的得分函数也随着增大，而且带来了不同的排序结果。因此类似的参数q不仅可以是决策信息范围的体现，也体现决策者对决策方案的偏好程度。若决策者对于决策方案存在较强的偏好关系，则可以赋予q一个较大的值；反之，若决策者对于决策方案的偏好程度较小，则会赋予q一个较小的值。

5.3 比较分析

为了验证该方法的优点，将本文提出的多属性决策方法与现有的方法进行对比。这些方法包括Liu和Wang[23]提出的基于广义正交模糊加权平均算子的多属性决策方法，文献[24]提出的基于广义正交Bonferroni平均算子多属性决策方法以及Wei等[25]提出的基于广义正交模糊Heronian平均算子的多属性决策方法。利用这些方法解决上述问题的得分函数值和排序结果如表3所示。

Table 2 Results with respect to different values ofkin q-ROFWMSM operator(q=3)表2 q-ROFWMSM算子中k取不同值的结果(q=3)

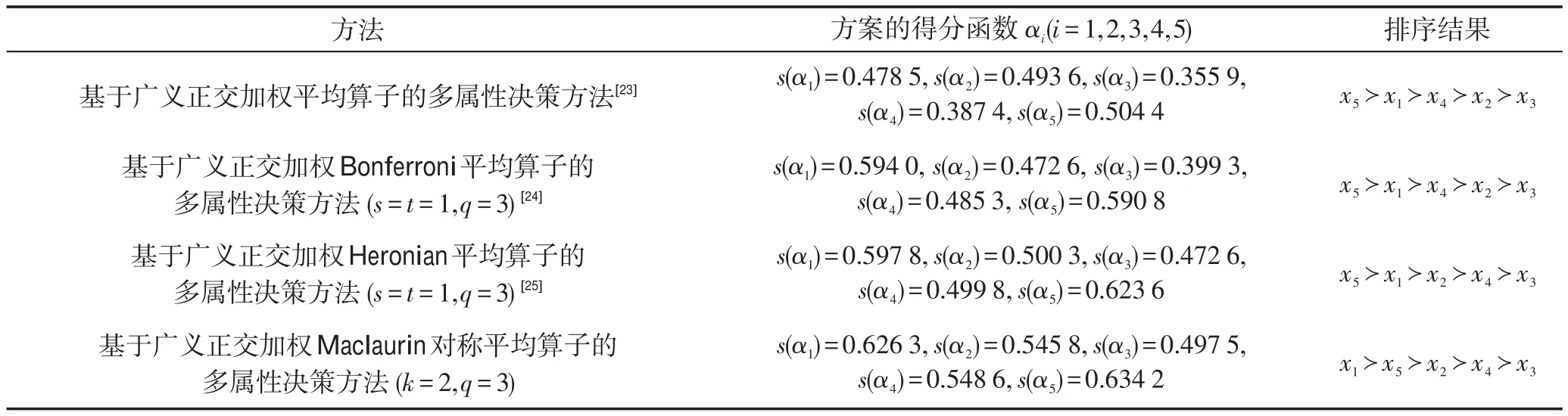
Table 3 Score function and ranking result by using different methods表3 利用不同的方法得到的得分函数和排序结果

从表3中可知，不同的决策方法所得到的得分函数值和方案排序的结果不相同。Liu和Wang[23]提出的基于广义正交加权平均算子的方法不能捕获变量之间的相关关系。即Liu和Wang[23]的方法认为变量之间是不相关的。然而在上述多属性决策问题中，属性之间具有相关性。例如企业竞争力(G1)和社会影响力(G4)之间是存在相关关系的。本文提出的方法是基于广义正交Maclaurin对称平均算子的多属性决策方法。该方法的优势在于能够捕获输入属性之间的相关关系。另外Liu和Wang[23]的方法是新提出的这种方法的特殊情况。因此本文提出的方法比Liu和Wang[23]的方法更强大，更灵活。文献[24-25]中的方法也能够考虑变量之间的相关关系，但是这两种方法只能考虑两个变量之间的相关关系。在实际的多属性决策问题中，输入变量之间往往存在着复杂的相关关系，因此在选择最优方案时不仅要捕获两个属性之间的相关关系，而且需要考虑多个变量的相关关系。而本文提出的多属性决策方法可以考虑多个变量之间的相关关系。而且如3.1节中所示，文献[24]中的方法其实是新提出的这种方法的特殊情况，因此相比于文献[23-25]提出的方法，本文提出的方法具有明显的优势。

6 结束语

本文在Maclaurin对称平均算子的基础上提出了一簇广义正交模糊Maclaurin对称平均算子。同时研究了这些算子的性质和特例。新提出的这些算子能够反映多个输入变量之间的相关关系，因而比现在的广义正交模糊集结算子更具有优势。另外基于这些算子提出了一种新的解决模糊多属性决策问题的方法。最后将该方法应用到实际问题中以验证该方法的有效性。实验以及比较分析表明新提出的多属性决策方法能够有效地解决多属性决策问题，并且比现有的方法更具有优势。下一步将继续研究广义正交模糊集的其他集结算子。