螺旋结构及梯度分析的图像融合算法*
2019-08-12高雷阜訾玲玲
杨 培,高雷阜,訾玲玲
1.辽宁工程技术大学 理学院,辽宁 阜新 123000
2.辽宁工程技术大学 电子与信息工程学院,辽宁 葫芦岛 125105
1 引言
图像融合是图像处理的关键技术之一,在军事、遥感、机器人等领域广泛应用,其目的是提高信息的利用率,最大限度提取同一目标的多源图像数据综合成高质量图像。为此,学者们相继提出许多图像融合算法[1-3],其中基于多尺度变换的方法,如小波变换[4]、轮廓波变换[5]、非下采样轮廓波变换(nonsubsampled contourlet transform,NSCT)[6]等,以其多尺度、多方向、各向异性以及平移不变等优点被广泛应用。但经这些多尺度变换后的低频图像系数不具备稀疏性,对图像的特征不能准确逼近。而稀疏表示(sparse representation,SR)是通过对源图像的分解建立细节特征和稀疏系数的映射关系,提取出图像更深层次的结构信息。因而,学者们将稀疏表示理论引入图像融合领域来解决多尺度变换的特征逼近问题[7-8]。Hu等[9]提出了基于SR和IHS(intensity,hue,saturation)变换的遥感图像融合,先对图像进行IHS变换,再用离散余弦变换(discrete cosine transform,DCT)字典进行稀疏表示,然后用绝对值最大融合规则对稀疏系数进行融合,最后通过重构和IHS逆变换得到融合图像。虽然达到了一定的融合效果,但其中的DCT字典进行稀疏表示时丢失了边界信息,绝对值取大的融合规则也易丢失图像间的结构信息。为此,严春满等[10]采用滑窗模型和K-SVD(K-singular value decomposition)字典学习算法对多聚焦图像进行融合,解决了稀疏表示的边界结构问题,但耗时较长。刘慧等[11]用NSCT变换和IHS变换进行结合,既克服了频谱失真问题,又保证了多方向性和平移不变性,但算法复杂度很高。赵春晖等[12]提出了一种快速的基于SR和NSCT变换的图像融合算法,稀疏表示采用4方向法(four-direction sparse representation,FDSR)提升融合效率,但在融合规则不恰当时易产生斜纹效果。
针对以上问题,本文提出了螺旋结构和梯度分析的图像融合算法。将待融合图像进行NSCT变换,对低频信息,利用螺旋处理前后的“2+2”方向结构图像数据进行字典训练和稀疏表示,既避免了传统滑动窗口带来的冗余计算量,又消除了FDSR的斜纹效果,再利用空间频率信息进行系数融合;对高频信息,先对其进行梯度分析,保留图像的结构信息,再采用最大模值优先进行融合;最后通过实验验证本文方法的有效性。
2 基础理论
2.1 NSCT变换理论
NSCT变换是由非下采样金字塔滤波器(nonsubsampled pyramid filter bank,NSPFB)和非下采样方向滤波器组(nonsubsampled directional filter bank,NSDFB)组成。NSCT变换如图1所示[6]。其中,NSPFB保证了多尺度特性,其特性是由移位不变滤波结构获得的,通过双通道非采样二维滤波器组实现了拉普拉斯算子的金字塔子带分解。NSDFB给出了方向性,将临界采样双通道扇形滤波器组和重采样相结合,构建树形结构的滤波器组,将二维频率平面分割成方向楔形,利用NSDFB得到位移不变的方向展开。
NSCT变换能够很好地分解出图像中的细节和近似光谱信息,而且在图像的分解和重构过程中,避免了对图像的上下重采样,使得各个子带图像与源图像的尺寸大小保持一致,解决了频谱混叠效应,使所表达的图像更精细。

Fig.1 Nonsubsampled contourlet transform图1 NSCT变换
2.2 稀疏表示和字典学习
稀疏表示是用字典中少量原子的线性组合来描述信号。设信号x∈RN,字典D∈RN×L,稀疏系数α∈RL,则稀疏表示问题可以描述为:

其中,||∙||0表示l0范数,表示非零元素的个数。这是一个NP难问题。Donoho和Candes等[13-14]已经证明在一定的条件下,l0范数可以转换为l1范数优化问题。进而,式(1)采用正则化方法可得到如下表达[15]:

其中,λ为正则化参数,用来均衡稀疏性和精度。这样的正则化稀疏模型有很多求解算法,最小角回归(least angle regression,LAR)算法是其中一种高效的解法[16]。
在图像的稀疏表示中,字典D的选取会影响到分解的稀疏度和重构的精度。构造字典主要有两种方法:解析方法和学习方法。解析方法由数学模型计算得到字典,获取简单且普适性高,但稀疏度和误差也高,如DCT字典等。学习方法通过样本数据进行字典训练,误差和稀疏度相对较小,但训练成本较高且普适性稍差,如K-SVD算法、ODL(online dictionary learning)[17]算法。K-SVD实时性较差,字典迭代更新时ODL的效率更高,因而本文采用学习方法在图像融合过程中进行字典训练,ODL算法进行字典学习,LAR算法计算稀疏编码,两者交替迭代,快速准确提取图像特征。
稀疏表示是在单尺度上对图像信息进行分析,与采用多尺度分析的NSCT变换进行结合,能满足多尺度上提取图像重要特征的要求。通过NSCT变换获得的图像低频信息,直接对其进行融合处理会导致无法获得图像中显著特征信息,并且变换中的多尺度分析需对图像进行分解和合成,易导致样本信息丢失,而稀疏表示中字典学习算法能对图像中的重要特征进行特征提取,恰好可以克服多尺度分析中的不足,并且字典原子是通过待融合图像信息训练而来,可以获得图像更准确的结构描述。故而本文在NSCT变换的多尺度基础上,对图像低频子图进行稀疏逼近表示再融合处理,对已经稀疏化的高频子图,通过梯度分析让边缘特征更加凸显后再融合,使最终获得的融合图像有更优的效果。
3 螺旋结构及梯度分析的融合算法
本文算法由两部分组成:第一部分是NSCT变换后低频子图中的螺旋结构设计;第二部分是高频子图的融合规则。在低频子图中采用螺旋结构,即是“2+2”方向稀疏表示进行字典学习、稀疏融合。高频子图中进行梯度分析后再进行融合。整体过程如图2所示。
3.1 低频融合过程
3.1.1 螺旋结构设计
稀疏表示融合规则中,图像经常被划分为大小相同的块,采用滑动窗口的形式对每个图像块进行稀疏表示和融合,滑动窗口的步长越小,融合效果越好。这种处理方式中,若融合规则不匹配,易出现空窗现象。此外,步长越小则计算量越大,在n×n大小的窗口滑动过程中,一个像素信息在步长为1时会被重复使用n2次,这极大降低了融合效率。文献[12]中放弃滑窗模型,用FDSR进行图像稀疏表示,重复计算次数从n2次降低到了4次且避免了空窗现象。虽然提供了更多的方向信息,但实验中发现这种处理融合图像易出现斜纹效果。对于二维图像来说,空间基底应是两个线性无关的向量。正交的向量组构成的空间更是适应人类视觉的感受。为了解决上述问题并且考虑空间图像的基底及其旋转前后的正交设计要求,本文提出了一种螺旋结构设计方法,也称之为螺旋处理前后的“2+2”方向稀疏表示(double_two direction sparse representation,DtDSR)。对源图像在螺旋处理前进行两个方向(45°方向和135°方向)稀疏表示,螺旋处理后又进行两个方向(水平方向和竖直方向)稀疏表示,具体过程如图3所示,即:
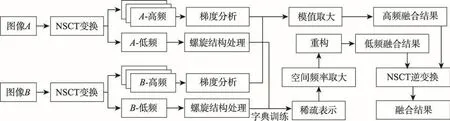
Fig.2 Flow diagram of proposed algorithm图2 本文算法流程框架图

其中,A0、B0分别为图像A、B的低频子图。
对于图像中任一像素点(边缘点除外)来说,周边有8个像素是其最近邻相关点,螺旋分析前的两个方向,保证了其对角线方向的4个像素依旧与原像素点最近邻,螺旋分析后所采用的两个方向,也较大限度拓扑同构了原像素点周边的结构性。此外,稀疏表示是对零范数NP难问题的凸优化处理,以便于利用相对成熟的凸优化理论和方法进行求解,故而采用稀疏字典对每个方向上的列或行像素进行稀疏表示以得到最优解,再进行系数融合。又因4个方向所获得的样本在处理过程中对任一像素均只使用一次,所占权重相同,因而在最终融合时,对所获得的4个不同方向上的融合图像进行平均得到低频融合结果。
在DtDSR结构模型中,每个像素信息仅被重复使用4次,相比于滑动窗口模型的每个像素被重复使用n2次(n为滑动窗口的长度)来说,所消耗的时间会大幅度下降,这也极大提高了融合算法的效率。
3.1.2 低频融合过程具体步骤
步骤1将低频子图A0、B0分别进行边缘扩展,避免后期稀疏表示出现边缘效应并进行45°、135°方向处理,各自得到训练样本A1、A2和B1、B2;将A0、B0分别进行螺旋结构处理后再进行水平、竖直方向处理,各自得到两个训练样本A3、A4以及B3、B4;具体处理过程如3.1.1小节所述。
步骤2对两组样本A1、A2、A3、A4和B1、B2、B3、B4根据式(2)分别进行ODL字典学习、LARs稀疏编码,得最优字典和稀疏系数,即:

步骤3对稀疏系数,采用文献[7]的系数融合方法,分别计算其空间频率,取值较大的作为融合系数,并同时选定对应的字典作为融合后的字典
步骤4重构图像,即:


其中,F表示最终的低频融合图像。
3.2 高频融合过程
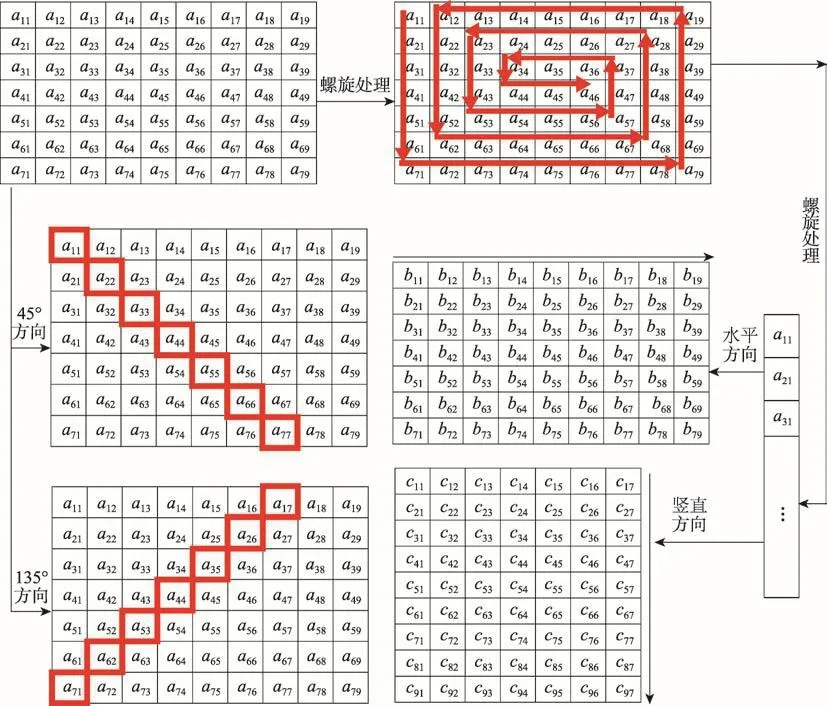
Fig.3 Schematic diagram of DtDSR structural model图3 DtDSR结构模型示意图
NSCT分解所得的高频子图含有图像的边缘和细节等突变特性。高频系数绝对值的大小反映这些特征变化的剧烈程度。对于图像的平滑部分,高频子图系数绝对值比较小;对于图像的高频边缘或者细节突变部分,高频子图系数的绝对值一般比较大。通常情况下,对于高频子图的融合常采用“模值取大”这一策略,但对于某些待融合图像来说,在同一部分都有突变,并且高频子图系数值都比较大,此时,选取到的高频子图系数容易使融合图像出现模糊现象。如图4所示,两张待融合图片分别为计算机断层成像得到的彩色图片A和核磁共振得到的灰度图像B,在有些边缘处如图中红框区域,视觉观察A较B模糊,但实验中,经过NSCT变换后得到的高频子图中,A系数的模值大于B的值,导致融合时会选取较模糊的A。为了减少这种现象的出现并且保持融合效率,提出一种基于梯度分析(gradient analysis,GA)的高频融合方法。
在图像处理中,图像的边缘可通过计算梯度求得,所得结果反映像素点灰度的最大变化率及其方向,能准确判断出图像边缘。若像素点处于图像边缘,则具有较大梯度值;若处于非边缘区域,梯度值很小或者接近零。此外,梯度运算也是图像边缘特征提取的高效方法之一,根据梯度的这些特性,将高频子图的边缘梯度表示引入“模值最大”这一融合策略中。如上例中A、B的高频子图,由于A的模糊性导致图中红框内边缘变化不明显,在同一边缘处经过梯度分析后得到新的系数后,A的梯度分析系数小于边缘比较清晰的B的值,融合时会选择B,这样会达到更好的融合效果。高频子图融合规则具体过程如下所示。

步骤1对A的高频子图,求其水平和竖直方向上的梯度表示矩阵,即:

Fig.4 Part of obtained graph data before and after gradient analysis图4 梯度分析前后部分数据图

步骤3根据图像A、B各尺度、各方向的梯度系数矩阵决定融合图像F的高频选取策略,如下式所示:
37 Attention of community population in Shanghai to chronic kidney disease and related influencing factors

3.3 融合过程算法步骤
输入:图像A、B。
输出:融合图像IF。
(1)对A、B进行NSCT分解,分解级数根据图像大小采用自适应方式进行选取,得到低频子图A0、B0和高频子图
(2)低频处理过程。由低频子图A0、B0,根据式(3)得到低频处理的训练样本,然后用式(4)得到各自的字典和稀疏系数。采用空间频率取大的方式得到融合系数和融合字典。再利用式(5)和式(6)得到最终低频融合图像F。
(4)将获得的F和进行NSCT反变换,获得最终的融合图像IF。
4 实验及结果分析
本文算法定义为DtDSR-GA,为了验证融合算法的性能,采用另外五种融合算法进行对比实验。基于SR的图像融合方法[18](SR)、基于小波变换和稀疏表示的图像融合算法[7](DWT-SR)、基于非下采样轮廓波变换和稀疏表示的融合算法[19](NSCT-SR)这三种算法中融合规则选取按照相应文献中的描述设定。此外,在NSCT变换的基础上,低频采用不同方向结构(FDSR、DtDSR)稀疏表示,融合规则同为低频分量稀疏系数空间频率取大,高频分量“模值取大”,算法分别记为NSCT-FDSR、NSCT-DtDSR。
为了能更好地凸显本文算法的效果,实验在相同基础条件下进行比较,五种对比算法和本文算法在稀疏表示时均采用ODL字典学习和LARs稀疏编码[20],正则化参数为0.15,迭代次数为10,滑动窗口大小为8×8,步长为1。DWT变换时小波基使用“db4”,分解层数设置为4层。NSCT变换时金字塔滤波器组选用“maxflat”,方向滤波器组采用“dmaxflat7”,分解尺度统一采用自适应于图像尺寸的方式,分解方向设置为8。本文算法利用Matlab R2014a编程实现,运行环境Intel®Core™i3-6100U CPU,4 GB内存,操作系统Windows 7。
4.1 评价指标
融合图像的质量评价是评估融合方法性能的重要手段,实验在主观评价的基础上,用客观评价作为辅助手段来验证算法的有效性。本文选取以下5个指标作为客观评价的标准[21]。在以下评价指标的公式中,F表示融合图像,R表示参考图像,M、N是图像F的大小,F(i,j)为F在(i,j)点的像素值。
(2)标准差(standard deviation,SD)
SD衡量图像灰度的离散程度。设是图像的平均值,则SD的计算公式为:
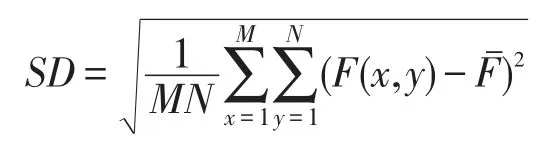
(3)空间频率(spatial frequency,SF)
SF表示图像中的空间像素总体活跃度。设fx、fy分别是x方向的行频率和y方向的列频率,则SF的计算公式为:

(4)平均梯度(average gradient,AG)
AG体现图像中的微小细节反差和纹理变化特征,其计算公式为:
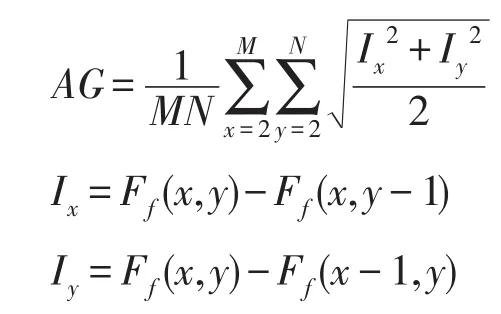
(5)平均结构相似度(average structural similarity,ASSIM)
结构相似度SSIM[22]是图像结构保真度的度量,其计算公式为:
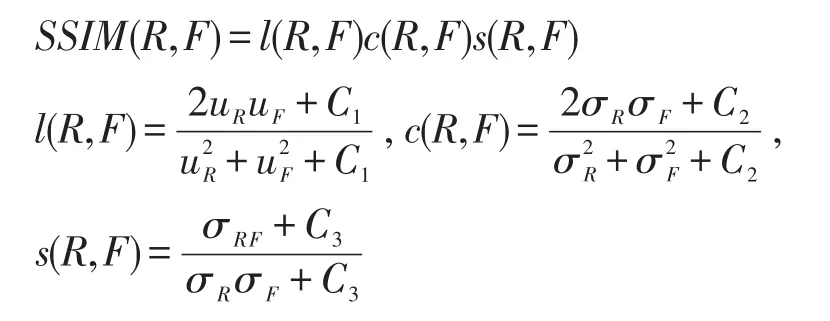
其中,l(R,F)、c(R,F)、s(R,F)分别是亮度、对比度、结构函数。uR和uF为平均值,σR和σF为标准差,σRF为协方差,C1、C2和C3是为了避免分母接近零而产生不稳定所添加的非常小的正常数。结构相似度越大,融合效果越好。为了减少评价误差,采取平均结构相似度ASSIM进行评价,其定义如下:

以上五种评价指标都是越大越好,对比实验表中最优指标由粗体标示。
4.2 实验待融合图像集
实验分别对灰度图像、彩色图像进行仿真实验,所采用图像均经过几何校正、图像配准等预处理步骤。实验数据包括“Disk”(256×256)和“Pepsi”(512×512)两组灰度图像集,以及“Street”(600×475)、“City”(256×256)、“Medical”(256×256)、“IR-visible”(640×480)四组图像集,如图5所示。
4.3 灰度图像融合实验
图6给出了灰度图像主观视觉融合效果图,所采用融合方法从左至右依次是SR、DWT-SR、NSCT-SR、NSCT-FSR、NSCT-DtDSR以及本文方法DtDSR-GA。观察图6可以看出,SR方法融合效果有模糊现象,DWT-SR方法所获取融合图像的清晰度稍逊NSCT系列方法和本文方法。尤其在Disk效果图中,本文方法明显要优于其他融合方法。
将Pepsi图像集及融合效果图中箭头和“P”中间部分放大,如图7所示,融合算法次序同图6一致。Pepsi图像集中白色偏斜纹,本文算法很好地在融合图像中继承下来,且图中箭头部分的字迹比较清晰。SR方法由于其融合规则的不足,融合图像清晰程度较低。DWT-SR融合方法因采用下采样操作,出现频谱混叠现象,在融合结果中表现出模糊锯齿状。NSCT-SR方法虽使得图像边缘变得清晰,但较本文算法依然有差距。NSCT-FSR、NSCT-DtDSR在图7中与本文算法效果没有过于明显的区别。
表1是灰度图像集融合结果的五种客观评价指标对比。由表1中可以看出,用本文提出的方法DtDSR-GA得到的融合图像,五项指标较其他算法都有提升。其信息熵IE、空间频率SF的提高,表明融合图像保留了源图像的大部分信息,轮廓清晰;标准差SD的提高,表明融合图像灰度变化剧烈,对比度较好;平均梯度AG的提高,表明了融合结果细节清晰程度。本文算法与NSCT-FSR、NSCT-DtDSR在图7中相比较没明显区别,但在表1中的数据显示其依然有较高提升。

Fig.5 Image data sets图5 图像数据集

Fig.6 Fusion result of grayscale images图6 灰度图像融合效果图

Fig.7 Local enlarged images of fusion effect in“Pepsi”图7 “Pepsi”融合效果局部放大图

Table 1 Comparison of evaluation indices of fusion results of grayscale image sets表1 灰度图像集融合结果评价指标对比
4.4 彩色图像融合实验
本文融合算法对于彩色图像或彩色与灰度图像之间的融合也同样适用,其流程如图8所示。

Fig.8 Flow chart for color image fusion algorithm图8 彩色图像融合流程图
实验的主观效果如图9所示,融合算法次序同图6一致。“Street”是多聚焦彩色图像,本文算法的融合效果明显优于其他算法。“City”是遥感图像,融合结果中采用NSCT分解后的视觉效果较优,本文算法在纹理结构上比其他算法更为清晰。“Medical”中彩色图像是显示人体组织血流和代谢功能的计算机断层成像图像,灰度图像是对软组织和血管清晰的分辨率高的核磁共振图像。融合效果图中,SR与NSCTSR算法色彩效果近似,但与源图像有较大差距。DWT-SR色彩效果同源图像近似,但结构信息模糊。本文算法融合效果不但在色彩上接近源图像,在纹理结构上也达到了较好的效果。“IR-visible”是可见光和红外图像,融合的色彩效果与源可见光图主观比较无色差。对于红外图像的烟雾弹亮点以及烟雾掩盖下的结构纹理部分,本文算法融合后效果更好。且通过表2客观指标对比,本文算法不但主观上效果良好,且客观指标较其他比较算法也都有所提高。
4.5 算法时效实验

Fig.9 Fusion result of color images图9 彩色图像融合效果图
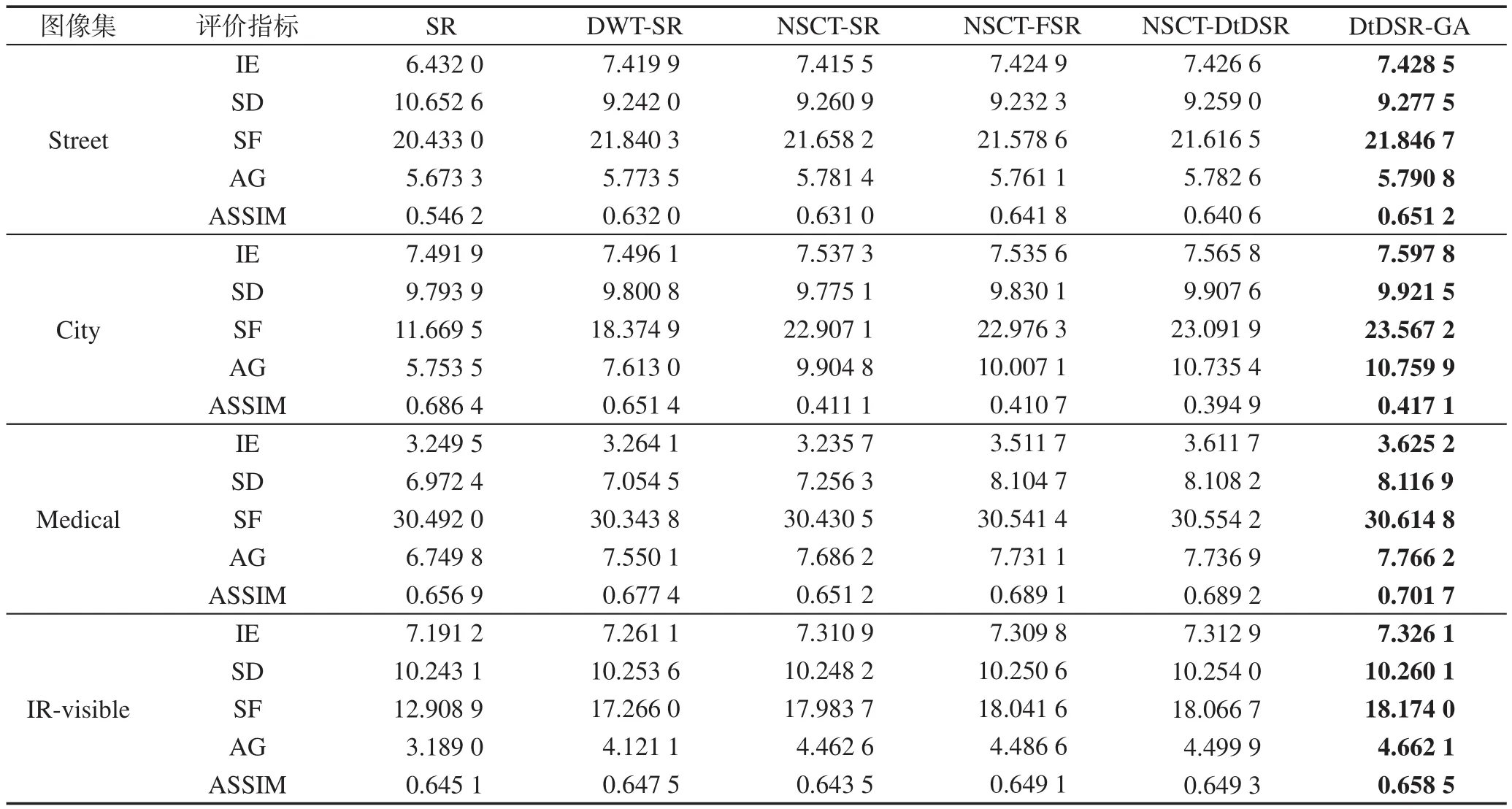
Table 2 Comparison of evaluation indices of fusion results of color image sets表2 彩色图像集融合结果评价指标对比

Table 3 Comparison of running time of different fusion methods for different image sets表3 不同图像集的不同融合方法运行时间比较 s
图像融合中,时效性也是评价算法的重要指标。本文算法在时间上的优势体现在低频融合时的DtDSR结构模型上,该模型中对图像的任一像素总共只使用了4次,而滑窗模型在步长为1,窗口大小为n×n时,对每个像素使用了n2次,样本数据量的减少使得本文算法复杂度在数量级上有较大降低,在时间上占有一定的优势。表3给出了实验中不同算法的融合时间。SR、DWT-SR、NSCT-SR方法采用滑窗模型,在步长为1,窗口大小为8时每个元素重复使用了64次,导致融合时间比较长。DWT-SR由于图像下采样,融合时间相对另两种方法有所降低。而NSCT-FSR、NSCT-DtDSR、DtDSR-GA采用方向模型,每个元素只用4次,提高了融合效率。NSCTDtDSR方法因增加了螺旋处理过程,运行时间比NSCT-FSR稍长,DtDSR-GA与NSCT-DtDSR相比,在高频处理中由于增加了梯度运算过程使得时间也稍增。与传统的滑窗模型的稀疏融合算法相比较,本文提出的DtDSR-GA算法数十倍提高了融合速度,虽在高频子图中因梯度分析使得时间有所增加,但从整体融合时间来说,增加时间与总时间的比值不超过3%。结合前文的主客观融合质量分析,DtDSRGA不但融合效率高,且融合质量也有所提高,证明了其有效性。
5 结束语
本文提出一种基于NSCT变换的图像融合方法,在低频子图融合中,提出一种螺旋处理的“2+2”方向结构模型进行字典学习和稀疏分解。在高频子图融合过程中,先对高频分量进行梯度分析处理后再采用“模值取大”的融合规则。通过实验证明,采用本文方法的融合结果在主观和客观上都具有一定的优势。本文的研究工作还可以有进一步的改进和应用,如,融合规则中可以采用多特征处理融合,采用本文稀疏处理方法尝试对彩色图像和RGB-D图像进行融合等。
