运用多元表征教学策略促进大班幼儿模式能力发展的行动研究
2019-08-11张迎春李娟沈童郑红玲王丽红李莹
张迎春 李娟 沈童 郑红玲 王丽红 李莹
[摘 要] 模式能力是幼儿形成逻辑思维的重要前提,对幼儿以后的数学学习和发展有着深远影响。为了提高幼儿的模式能力,本研究采用行动研究范式,运用多元表征的教学策略对实验班和对照班幼儿各30名进行为期4个月的干预,结果发现在行动研究结束后,实验班幼儿的模式能力在量和质两个方面都获得了提升。就量的方面来说,实验班幼儿的模式能力在前后测及与对照班的对比中都有明显提升。就质的方面来说,实验班幼儿更加胜任模式的创造和转换任务,能够把模式概念运用于日常生活中,并且乐于开展模式活动。参与行动研究的教师对多元表征教学策略不再“抵触”,运用多元表征教学策略的能力得到了提高。合理的干预方案和研究小组成员的协作是行动研究富有成效的关键因素。教师在数学教学中应善于帮助幼儿理解数学关系,鼓励幼儿选择多种方式进行表征,并在日常生活中注重对幼儿多元表征意识的培养。
[关键词] 模式能力;多元表征;行动研究
一、问题提出
模式“反映的是客观事物和现象之间本质、稳定、反复出现的关系”。[1]模式作为“任何可复制的规律”,具有重复性和可预测性。[2]儿童对模式关系的理解和认识,不仅有助于儿童通过模式的概括去发现、理解数学自身独特的结构以及数、几何、测量等各大主题之间的联系,使儿童获得有效的数学图式,而且能够为其以后抽象的数学知识(如函数、代数观念)的学习奠定基础,促进儿童对数学与其他学科之间联系的理解和掌握。[3]
而模式表征是模式这一概念的重要组成部分,关于数学表征,不同的学者有不同的解读。有学者认为数学表征是指“运用其他的形式表达数学概念或关系的过程”。[4]也有学者补充“数学表征不仅仅是指儿童用某种形式,如数学符号、图表及口头表达等,表达要学习的或处理的数学概念或关系,还包括儿童在解题过程中转换表征方式的能力”。[5]而多元表征这种“提供多样化的、弹性的信息呈现方式,让学习者分别使用文本、图片、声音、动画、多媒体等来显示同一知识点或学习对象的形式,能最小化学习障碍,最大化学习机会”。[6]因为在数学教育中,多元表征方式可以帮助学生更加深入地理解数学的概念以及概念之间的关系,提高学生问题解决能力,增加数学学习的趣味性。
但是,我国的学前数学教育中,没有给予模式及其多元表征应有的重视。在实践中,模式尚未作为一个独立的概念被提出来,而是和数学领域中序列、样式混在一起。[7]且在当前的幼儿园模式教学中,存在着操作材料单一、模式教学较多停留在视觉层面等问题,这些问题限制了儿童对模式本质的理解和认识。[8]那么,针对当下模式教学的不足,我们应该如何促进幼儿模式能力的发展呢?黄瑾(2015)指出,教师应该“鼓励幼儿从视觉、听觉、动觉上去感受相同的模式规律性,帮助幼儿尝试将模式的一种表征形式转化为另外一种表征形式”。[9]杜青霞(2014)按照表征的形式(感觉通道)也提出,数学表征主要包括听觉表征、视觉表征和动作表征,且三者一般都是相互伴随出现。[10]
然而,在教育實践中,到底该如何设计具体的教育活动,如何帮助一线教师掌握利用多元表征模式来促进儿童模式概念的获得,进而把这种多元表征模式迁移到其他教育活动中呢?传统上,给教师单纯讲授知识的方式效果并不太好,[11]让教师在实践中开展行动研究是大家公认的促进其专业发展的有效形式,[12]因为行动研究中获得的知识能够让教师们灵活地处理复杂的、多样的课堂情况,并使知识得到迁移。[13]本研究正是采用协同式行动研究范式,由幼儿园一线教师、H大学学前教育专业硕士生导师、学前教育专业的研究生组成研究共同体,以促进儿童模式能力发展为出发点,对幼儿进行为期四个月的多元表征(听觉、视觉和动作)教学干预,以此来探析多元表征教学模式及其效果。
二、研究方法
本研究采用行动研究范式。行动研究,是指由社会情境(教育情境)的参与者(教师、校长、学校辅导员或其他教学相关人员)为提高对所从事的社会或教育实践的理性认识,为加深对实践活动及其依赖的背景的理解所进行的反思研究。[14]本研究是基于实践中模式教学的不足而对多元表征教学有效性进行探析的研究,而行动研究则是一种“与教育具体实践密切相关,由一线工作者与教育学者共同参与,以行动进行研究,以研究促进行动的实践性研究方法”。[15]因此,本研究与行动研究的思路相切合,故选择此研究范式。
(一)研究对象
本研究的研究对象来自于河北省保定市Q园, Q园是一所省级示范幼儿园,但是在幼儿数学方面的实践研究经验并不丰富。已有研究表明,大班幼儿基本上开始具备模式转换的能力,也就是多元表征的能力,而小班和中班幼儿一般还不具备。因此,本研究选择大班幼儿作为行动研究实施的对象。Q园一共有6个大班,其在实施幼儿数学教育时参考来源有两个:一个是Q园自主研发的园本教材,另一个是Q园购买的幼儿数学教育教材。
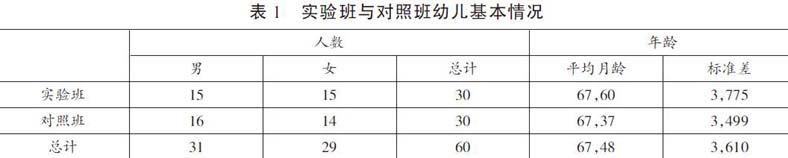
本研究从Q园6个大班中随机抽取2个班共60名幼儿作为研究对象,一个班为实验班(30人),一个班为对照班(30人),具体情况见表1。
(二)行动研究干预方案
1. 行动研究小组成员介绍。
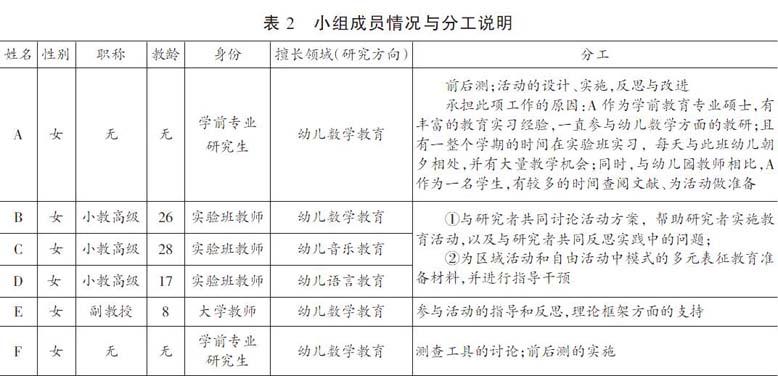
行动研究既可以是个人的,也可以是多人协同合作的。本研究采用的是多人合作模式,由学前教育专业研究生、实验班级教师、H大学学前教育专业硕士生导师共同构成行动小组。各成员的基本情况与分工如下页表2所示:
2. 行动期间,实验班与对照班模式教学的基本情况。
在行动研究期间,实验班模式领域的教学没有实施Q幼儿园园本教材和专门数学教材中的相关内容,而是由行动研究小组按照多元表征的原则设计实施模式领域的教学;对照班模式领域的教学由其本班教师实施,教学内容来自Q园的园本教材和专门的幼儿数学教材。Q园有基本的教学进度要求,因此,两个班实施的模式方面教育活动数量基本一致,不同的只是教育形式,即实验班更加注意多元表征下的模式教育,对照班对此并无特意关注。
在行动研究期间,Q园同意由研究者A执教并提供测查场地的行动小组定期交流的会议场所,为整个行动研究的顺利实施提供了便利。
3. 干预方案的具体介绍。
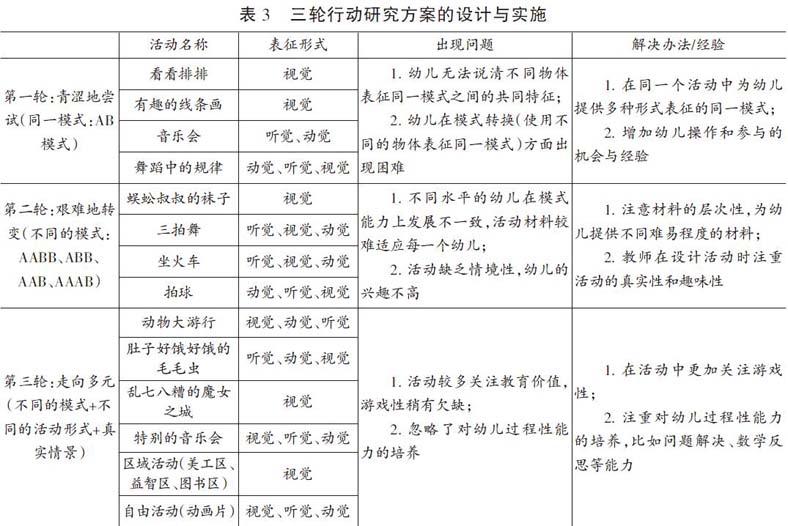
行动研究是一种“动态生成性研究”,其在不断变化的教育实践中实施,因此,研究者需要根据实践中遇到的问题边研究边修改方案。[16]在本研究中,除了第一轮行动方案根据大班幼儿模式能力的前测结果制定,第二、三轮的研究方案则是结合前一轮行动研究过程中遇到的问题而制订。详见下页表3。
在模式类型方面,主要分为重复性模式和发展性模式。周葱葱、林泳海提出幼儿式样(模式)的发展经历了“从循环式样发展到重复式样,再发展到滋长式样(递增模式或发展性模式),最后发展到变异式样”。[17]因此,在前两轮的行动研究中主要涉及重复性模式,在第三轮的行动研究中涉及发展性模式。
在模式结构方面,涉及多种结构的模式。[18]在第一轮的行动研究中,主要涉及AB结构的模式,到后期进行反思的时候,研究者与行动小组一致认为:单一的模式结构会使幼儿在强化的过程中记住某一模式,而不是真正地掌握模式的本质,因此,在后两轮的行动研究中,会涉及多元的模式结构。
在表征形式方面,本研究在杜青霞(2014)的分类基础上,将表征形式定义为视觉、听觉、动觉上的表征,并据此进行模式活动设计,但每节活动涉及的表征形式并不固定,由活动内容本身决定。
在活动形式方面,既包括集体活动也包括区域活动和自由活动。对大班儿童模式能力的前测表明,大班幼儿在模式转换方面的分数普遍较低,即普遍不擅长模式的多元表征。所以行动之初,行动小组想用集体教授的方式,让幼儿感知多元表征的形式。但是随着行动研究的深入,我们越来越认识到在区域活动和自由活动时,存在大量模式多元表征的机会,所以在第三轮行动研究时,加入了这两种活动形式的干预。
具体的活动方案如表3所示:
(三)测查工具
在参考史亚娟(2003)[19]、杨铮铮(2007)[20]、高燕(2009)[21]、陆敏[22]等人的研究成果及《3~6岁儿童学习与发展指南》模式部分的测查题目的基础上,本研究结合大班幼儿年龄特点自行编制了测查工具,根据预测查的结果对测查工具进一步修改;随后结合学前数学教育领域两名专家的意见,最终形成了正式测查工具。且本研究是测查幼儿的外显行为,评分标准也简单易操作(幼儿正确完成任务计1分,错误计0分),因此测查工具信度较有保证。
测查题目主要从表征形式(视觉、听觉、动觉)、模式类型(重复性模式和发展性模式)、模式能力(模式复制、模式填充与扩展、模式创造、模式转换)三个维度进行设计,共21道题。具体包括:
1. 听觉的模式:包括重复性模式(ABC)和发展性模式(ABABBABBB)。①ABC 结构的模式:主试展示三种不同乐器并按规律敲出声音,重复一次以后,请幼儿敲出听到的规律,并询问幼儿“接下来是什么”,最后请幼儿用不同的方式表示这个声音的规律;②ABABBABBB结构的模式:主试播放“猫—狗—猫—狗—狗—猫—狗—狗—狗”的叫聲,重复一次以后,请幼儿模仿听到的声音,并询问幼儿“接下来应该怎么叫”,然后请幼儿用不同的方式表示这个声音的规律;幼儿听完两个有规律的声音之后,主试请幼儿使用一种、两种或三种乐器创造与教师不一样的声音模式。
2. 动作的模式:包括重复性模式(ABC)和发展性模式(ABABBABBB)。①ABC 结构的模式:主试做出“拍肩—拍手—拍腿—拍肩—拍手—拍腿—拍肩—拍手—拍腿”的动作,重复一次以后,请幼儿重复主试的动作(三组以上),并询问幼儿“接下来是什么”,最后请幼儿用不同的方式表示这个动作的规律;②ABABBABBB结构的模式:主试做出“拍肩—蹦—拍肩—蹦—蹦—拍肩—蹦—蹦—蹦”的动作,重复一次以后,请幼儿重复主试的动作,并询问幼儿“接下来应该怎么做”,然后请幼儿用不同的方式表示这个规律;主试做完两个有规律的动作以后,请幼儿做出与主试不一样的规律动作。
3. 视觉的模式:包括重复性模式(ABC)和发展性模式(ABABBABBB)。①ABC结构的模式:主试摆出“圆形—正方形—三角形—圆形—正方形—三角形—圆形—正方形—三角形”规律的模式(不同色,且颜色没有规律),请幼儿摆出这个模式,并询问幼儿“接下来是什么”,最后请幼儿使用不同的方式表示这个规律;②ABABBABBB结构的模式:主试摆出“兔子—胡萝卜—兔子—胡萝卜—胡萝卜—兔子—胡萝卜—胡萝卜—胡萝卜”(同色),请幼儿摆出这个模式,并询问幼儿“你知道接下来应该摆什么吗?”,然后请幼儿使用不同的方式表示这个规律;幼儿看完两个规律后,主试请幼儿用兔子和胡萝卜的图片摆出自己的模式。
(四)测查计分
行动研究之初,研究者对60名幼儿的模式能力进行了前测,利用spss22.0软件分析大班幼儿的得分情况以及大班幼儿在模式活动中的表现和特点。然后历时4个月,研究者又对幼儿进行了后测,以探究经过行动研究,实验班幼儿的模式能力是否发生变化。主试根据幼儿在测查中的表现进行评分,在模式复制、模式扩展任务中采用“0、1”计分,“0分”表示不能完成任务,“1分”表示能够完成任务。在模式创造、模式转换任务中采用累积计分,即只要儿童创造或转换出一种形式,就计1分,分数可以累计;如果一种都无法创造或转换,则计0分。
这里需要说明的是,前后测的题目结构、难度都一样,只是稍微变化了一下呈现的材料,比如前测时使用的是雪花片,后测则改为小木块。前测使用的是小兔子和胡萝卜,后测使用的则是小狗和骨头。又由于前后测时间相差4个月之久,所以避免了练习效应。
三、研究结果与分析
(一)量的分析
1. 大班幼儿模式前测得分总体情况。
根据大班幼儿(60名)在前测中完成任务的得分情况可以得出,模式总分最高分为27分,最低分为1分,平均分为10.78分,标准差为5.906。在对幼儿模式得分进行正态分布检验时(见图1),得出偏度系数Skewness=0.792,峰度系数Kurtosis=0.309,两个系数都小于1,可认为近似正态分布。由此可以看出,本次测查工具的难度适宜大班的幼儿。
2. 不同模式类型的前测得分情况。
在对60名大班幼儿的前测中,幼儿在不同知觉、不同模式能力以及不同模式结构的得分情况详见表4:
由表4可知,在各项知觉方面,幼儿动觉的模式平均分最高,而视觉和听觉的平均分则相同;在模式的各项能力方面,幼儿的复制能力平均分最高,其次是模式扩展能力,然后是模式创造能力,模式转换能力的平均分得分最低,这也就说明幼儿缺乏表征模式的能力;在模式结构方面,幼儿的重复性模式平均分最高,而发展性模式得分较低。
3. 实验班与对照班的幼儿在前后测中的得分情况。
由表5可以得出,将对照班幼儿、实验班幼儿的前后测模式得分进行配对样本t检验,发现在行动研究的4个月内对照班幼儿的模式能力无显著变化(P=0.292>0.05),这意味着传统的模式教学方式在促进大班幼儿模式能力的发展上效果不明显。而实验班幼儿在行动研究的前后测查中有显著性差异(P=0.000<0.001),这表示了经过三轮的行动研究干预,幼儿的模式能力获得了明显提升,也意味着多元表征教学的有效性。
注:前测中N=30;后测中个别幼儿流失:实验班N=28,对照班N=27;*P<0.05,**P<0.01,***P<0.001(下同)
4. 实验班与对照班幼儿在前后测中的模式水平对比。
由下页表6可以得出,在前测时,两个班级的幼儿模式水平无明显差异(P=0.116>0.05),即在行动干预之前,两个班的幼儿模式发展水平接近。而在实验班经过三轮行动干预、对照班进行常规的模式教学活动后,发现两班幼儿的模式水平出现了明显差异(P=0.000<0.001)。因此,与传统的模式教学相比,多元表征教学能够更好地促进大班幼儿模式能力的发展。
(二)质的分析
经过三轮行动研究干预后,研究者对实验班幼儿的表现进行了质性分析:每天记录下儿童和实验班教师的行为表现,并收集行动小组教师的反思日志。最后,从一手资料中,编码出幼儿和教师通过行动研究发生的改变。
1. 儿童的变化。
(1)认知方面——“模式创造与转换”方面更加胜任。
从前测数据可知,儿童的模式复制和扩展能力发展较好,而模式创造和转换能力相对较差,这体现了模式能力发展的递进性,即在模式的各项能力中,模式识别是基础,随后发展起来模式的复制、扩展、创造、转换能力。虽然模式的创造和转换能力发展对幼儿来说较有挑战,但是在幼儿早期的模式学习中,模式的创造和转换能力都体现了幼儿思维的灵活性。[23]因此,在进行模式活动设计的时候,研究者重点关注培养幼儿的模式创造和转换能力,幼儿在行动研究过程中也获得了此方面的发展。例如,在区域活动中,幼儿在用动物贴画来做出自己的模式时,某幼儿提议说可以用笔把自己的模式表示出来,于是其他幼儿也开始尝试用符号来表示自己的模式;在集体活动中,当幼儿自由选择材料进行表征时,有的幼儿会根据自己的喜好主动要求使用乐器(教师未事先提供),当教师提供之后,会主动和其他幼儿结伴使用不同的乐器表现某种模式。这些都体现了在行动研究过程中,幼儿在模式识别的基础上,已经初步获得了模式创造和转换的意识与能力。
(2)行为方面——在生活中主动运用模式。
儿童在行为方面的变化表现为实验班的幼儿逐渐能够将模式知识与生活联系起来。随着行动研究的逐渐深入,幼儿的行为开始发生了一些变化,比如幼儿开始主动地用模式装饰自己的作品(绘画作品、相框等);能够关注到生活中有规律的事物(如楼梯、栅栏);在区域活动时能够自己提出用另外一种方式表示同一模式;在阅读和其他的自由活动中,幼儿能够主动使用模式去解决问题。
户外活动时间,有的幼儿在跳绳,而忘记带跳绳的幼儿则用粉笔在地上画画,地上有圆圈且均匀地划分为几个部分,有个幼儿说要装饰成一个大蛋糕,在装饰的过程中,幼儿用不同的颜色填充不同的空间,并且颜色的排列有自己的规律(最内圈是一个红色大圆点,第二圈是黄蓝模式,第三圈是白绿模式,第四圈是粉色重复模式)。
———2017年10月19日,行动小组成员A
(3)情感方面——乐在其中地“学习”。
在幼儿的情感方面,表现为幼儿对参与模式活动的兴趣提高。在第一轮行动研究的时候,研究者一直在重复AB这一模式,这导致在第一轮后期,幼儿参与AB型规律活动的兴趣有所下降。为了提高幼儿在活动中的兴趣,在第二轮行动研究时,研究者增加了模式结构的多样化;在第三轮行动研究的时候,增加了更多的活动形式,比如动画片、绘本、贴画、手指谣等,这都使得幼儿在游戏的过程中获得了模式能力的发展。
在区域活动中,当教师将贴画投入到美工区以后,美工区幼儿的数量迅速增加,最多的时候有8个幼儿同时进入到美工区,他们有的用贴画创造自己的模式,有的用笔画出的符号表示模式。在《亂七八糟的魔女之城》活动结束以后,研究者将绘本投入到阅读区,在自由阅读时间,幼儿开始争先恐后地去阅读这本书,阅读过程中,幼儿一边认真地看故事中的情节,一边寻找这本书中的模式,并与同伴交流。在研究者播放动画片《呜咪123》时,出现模式内容幼儿也能够投入到剧情里面,跟随动画片的要求,解决动画片中模式的问题,如在第2集中呜咪兄妹在寻找拉绳时,需要小鸟们唱一首特别的歌“啾啾—滋滋—啾啾—滋滋—啾啾—滋滋”,当一个小鸟不会唱时,为了帮助小鸟,幼儿会主动跟着一起有规律地唱这首歌;在第34集中,为了从果酱中救出小鸡,需要幼儿教小鸡朝一个方向有规律地移动,即“扭扭—扭扭—拍打—扭扭—扭扭—拍打”,幼儿们都很开心地晃动自己的身体教小鸡如何移动。这些都体现了幼儿对模式活动浓厚的兴趣。
2. 行动小组成员的变化。
(1)态度认知方面。
在对教师进行访谈的时候,发现幼儿园教师在数学教学中很少开展多元表征教学,其主要原因集中表现为以下两个方面,一是教师本身对多元表征教学不了解,不愿意使用多元表征策略进行教学;二是使用多元表征需要教师投入更多的时间和精力去设计教学活动,因此,有些教师就会选择使用单一的教学方式。基于以上这种情况,行动研究的重点就是我们不断学习和讨论如何有效地实施多元表征教学,包括阅读相关理论、头脑风暴、辩论、总结。
从第一轮的摸索到第二轮的艰难转变,再到第三轮的真正多元,我们看到了幼儿对多元表征教学活动的喜爱,看到了他们模式能力的提高,尤其是幼儿在模式转换能力上(多元表征方面)的提升。在这个过程中,行动小组的教师对多元表征教学的态度也都发生了变化。
在最开始听到“多元表征”的时候,我是很懵的,因为我以前没有听过这个概念,也不知道在教学中如何使用多元表征策论。随着行动研究的进行,我渐渐改变了看法,这才发现除了传统的、单一的知识点教授,教师也可以使用更多的方式和途径进行教学,所以,在以后的教学中,我会尽量采用多元表征的教学策略。
——2017年11月17日,实验班教师C
(2)教学能力方面。
行动研究是一个动态过程,在这个过程中,能够鼓励教师“深入观察教学动态,仔细分析学生的行为和互动情况,验证挑战现有的实践惯例,敢于尝试新的教学方法”,[24]即使在这个过程中,教师遇到了失败,也是有实际的借鉴意义的。在前两轮的行动研究过程中,虽然行动小组的教师在实施多元表征模式教学活动的时候遇到了困难,但是经过一次次并不完美的尝试后,研究者和行动小组教师吸取经验并积极调整教学活动,最终走向了多元表征的教学活动。在这个过程中,我们对如何运用多元表征进行模式教学进行了多次实践,从开始的单个模式结构到后来的多样模式结构,从开始的单一模式难度到后来有层次的任务提供,从开始的单一集体教学干预到后来对区域、生活活动的干预,从开始过于注重核心经验的传授,到后来对游戏性、情境性更加关注……这些摸索,使我们更加深刻地了解了多元表征教学策略的意义,掌握了多元表征教学开展的步骤,同时也期待着更多多元表征的策略运用到其他领域的教育实践中。
四、讨论与教育建议
(一)讨论
经过四个月的行动研究干预,无论在量的方面,还是在质的方面,实验班幼儿的模式能力都获得了提升,从而验证了多元表征教学的有效性。这种有效性不仅体现在后测分数的显著性提高,还体现在幼儿对模式概念的热情,幼儿能主动把模式概念运用于生活,行动小组成员对多元表征教学策略不再“抵触”,运用多元表征教学策略的能力得到了提高。下面对本研究能够取得成效的原因尝试作总结:
1. 行动研究方案设计合理,实施中不断反思。
行动研究是针对实践中的问题而进行的研究,具有“反馈—调整性”的特点,即研究者可以根据实践中发生的情况对活动的目标、结果和手段进行调整。[25]在本研究中,行动研究方案的设计目的是为了解决当前模式教学中表征单一的问题而尝试探索多元表征的教学策略。
首先,我们根据前测结果,设计了初始方案,干预的重点放在了模式创造与转换这两个方面,并依据文献与实践情况,把多元表征确定为动觉、视觉、听觉三个层面。其次,我们针对行动研究中出现的问题,随时讨论调整。美国教育家波斯纳曾指出,“没有反思的经验是狭隘的经验,至多只能成为粗浅的知识”,[26]在行动研究实施的过程中,行动小组教师会在每一轮活动结束后及时针对活动中方案的设计、教师的教学表现、幼儿的表现三个方面进行反思,讨论并撰写反思日志,反思日志的撰写可以帮助行动研究者“返回去”寻找观念的根据、“跳出来”思考自己的行为和观念,这些都有助于行动研究中的教师对当前的活动进行反思,在总结经验的基础上,进行下一次教育活动。[27]比如当我们发现单一AB结构不利于调动儿童的兴趣增强对模式概念的掌握时,随即增加了其他结构;发现区域与生活活动无法与多元表征的集体模式教学形成合力时,则对区域和生活活动进行了干预;发现我们过于重视模式核心经验的倾向时,则加入了对幼儿过程性能力获得的关注;等等。
2. 行动小组协同合作。
行动研究既可以是个人的,也可以是多人协同合作的。本研究采用的是多人合作模式,由学前教育专业研究生、实验班教师、大学教师共同构成行动小组。协同合作的形式,可以集思广益,为行动研究方案的制订、实施、讨论与反思提供多维度的思路,同时,高校研究者的参与可以为行动研究提供理论上的指导。[28]
在行动研究实施的过程中,行动小组成员共同制订干预计划,然后由学前教育研究生A实施行动。期间,A与三位实验班教师针对每节活动及时讨论并撰写反思记录。在每一轮行动研究结束后,A与大学教师E共同针对本轮行动研究的优点和不足进行反思,以便在下一轮行动研究中进行改进。四个月的行动研究结束后,行动小组的教师在对多元表征教学的态度上更加积极主动,同时,运用多元表征教学的能力也有所提升。
(二)教育建议
1. 帮助幼儿理解数学的关系并能够选择恰当的方式进行表征。
数学是一门高度抽象的学科,学前阶段的幼儿处于具体形象思维阶段,对数学中的内在逻辑关系的理解较为困难,而多元的表征方式可以通过纵向、横向、纵横相结合呈现数学概念的形成过程,有助于学生理解数学概念的本质内涵,把握数学概念的外延特征,实现数学概念的科学建构。[29]但是,已有相关研究还表明,在学某些数学概念时,不适宜的表征形式并不能帮助幼儿解决数学问题,反而会增加幼儿认知学习的负担。[30]因此,教师在进行教学时,应根据教学内容去选择适宜的表征方式,不能一味地“求多”。比如《音乐会》这个活动中,既有音乐(听觉表征),又可以非常自然地加入随音乐而起的动作表征。但是,在《乱七八糟的魔女之城》这个活动中,因为这是一节绘本阅读活动,注重幼儿在活动过程中对绘本内容的理解程度,所以这节活动更适合视觉上的表征,如果一味求多,则会对幼儿的理解造成障碍。
2. 在日常生活中注重对幼儿多元表征意识的培养。
黄瑾(2011)指出学习者通过学习多元表征,可以在两种或多种不同的表征形式之间进行转换,这有助于学习者对某一概念的完整架构,对学习内容的含义也将有更深的理解。[31]但是,幼兒数学多元表征能力的培养,不能仅仅通过几节集体活动就实现,更需要教师能够在日常生活(区域活动、生活环节等)和其他领域活动中,抓住教育契机,创设多元表征的任务。比如在户外排球的时候,教师就可以引导儿童有规律地拍球,在音乐活动中引导幼儿发现音乐中蕴含的听觉模式等。
跳出模式概念的多元表征,从更广泛的儿童表征来看,幼儿往往会选择自己擅长的方式去表征问题,这就需要教师在幼儿表征的基础上,鼓励幼儿尝试其他形式进行表征问题,如游戏“你划我猜”中对身体动作的观察、天秤游戏中用各种符号记录结果、用身体动作表征母鸡萝丝走过的路线等,都体现了数学概念的不同表征形式。总之,教师应该在各类活动以及游戏中鼓励幼儿运用多感官去感受数学的概念,并尝试用多元的方式将概念表征出来,以促进幼儿数学思维的发展。
3. 关注幼儿数学过程性能力,从而促进幼儿数学概念的理解与运用能力。
数学能力分为内容性能力和过程性能力,内容性能力是大家较为熟悉的数概念与运算、集合与分类、模式、几何与空间等关键概念的获得。数学过程性能力描述的是学生知道如何学习、理解和应用数学的能力,它强调的是“获得和运用知识的方法”。[32]这一过程性能力对幼儿终身学习、数学素养的养成和数学概念的获得都至关重要。[33]
我们的行动研究在第三轮干预中,着重关注了幼儿数学过程性能力的培养,因为诸多研究证实,教学中对学生数学过程性能力的关注,是儿童获得数学内容知识的有力支撑,它能够提高学生对某个概念的理解能力,从而提高数学学业表现。[34][35]之所以如此,是因为儿童在面临一个数学问题时,会激发他们之前储存的数学知识,并激发他们运用多种策略。在这个过程中,儿童会回忆、练习、运用数学内容性知识。[36]与此同时,在问题解决过程中,儿童去探索一个未知的问题,情感是好奇的、积极的。[37]当我们引导儿童关注某个数学概念与生活之间的关联时(数学关联能力),他们会不自觉地把自己的兴趣置于实际情景的应用中,[38]不仅让他们认同数学的有用性,还会在实际情景中更好地理解抽象数学概念。
然而,在教育实践中,一线教师往往对其关注不够。[39]望本行动研究能够在一定程度上引起教师们对幼儿数学过程性能力的关注。在数学活动中,不仅要心存数学内容知识方面的“关键概念”,还要关注儿童的问题解决能力、推理验证能力、数学交流能力、数学表征能力及数学关联能力。
参考文献:
[1]史亚娟,庞丽娟,陶沙,等.儿童数学认知能力发展的影响[J].心理发展与教育,2003(4):47-51.
[2]LYNN M, MCGARVEY. Is it a pattern?[J]. Teaching Children Mathematics,2013(5):564-571.
[3]MARINA M, PAPIC J T, MULLIGAN M C, et al. Assessing the development of preschoolers mathematical patterning[J]. Journal for Research in Mathematics Education,2011(3):237-268.
[4]姜慧慧.义务教育阶段学生数学表征能力的测评[D].上海:华东师范大学,2014:5-6.
[5][39]周晶.5~7岁儿童数学过程性能力的构成要素及应用研究[D].上海:华东师范大学,2016:60-63.
[6]唐剑岚.数学多元表征学习及教学[M].南京:南京师范大学出版社,2009:45.
[7]章佳颖.4~6岁儿童数学认知中多元表征研究[D].上海:华东师范大学,2011:11-21.
[8]張亚杰.提高幼儿园数学模式的有效性[J].上海托幼,2012(3):12-13.
[9]黄瑾,田方.学前儿童数学学习与发展核心经验[M].南京:南京师范大学出版社,2015:59-60.
[10]杜青霞.高中生数学概念多元表征的调查研究[D].武汉:华中师范大学,2014:3-12.
[11]HRAGREAVES A. Transforming knowledge: blurring the boundaries between research, policy, and practice[J]. Educational Evaluation and Policy Analysis,1996,18(2):105-122.
[12]ELLIOTT J. Action research for educational change[M]. Milton Keynes: Open University Press,
1991:78.
[13]HO C L . An investigation of preschool teachers ways of seeing action research using phenomenography[J].Educ Res Policy,2016(15):147-162.
[14]陈向明.质的研究方法和社会科学研究[M].北京:教育科学出版社,2000:448.
[15]孙杨丽.运用多元表征教学策略进行中班几何图形教学的行动研究[D].天津:天津师范大学,2014:9-17.
[16]李子彪.行动研究及其推广的意义[J].广州教育,1992(6):16-20.
[17]周葱葱,林泳海.3.5~6.5岁儿童式样认知发展的实验研究[J].心理学探新,2003(1):33-36.
[18]黄瑾.幼儿园数学教育与活动设计[M].北京:高等教育出版社,2010:163-164.
[19]史亚娟,庞丽娟,陶沙,等.3~5岁儿童模式认知能力发展的研究[J].心理发展与教育,2003(1):46-51.
[20]杨峥峥.4~5岁儿童模式与排序能力发展的研究:城市与农村儿童的比较[D].上海:华东师范大学,2007:5-12.
[21]高燕.小班幼兒模式认知能力及其培养研究[D].南京:南京师范大学,2009:5-45.
[22]陆敏.多元表征学习在幼儿园数学活动中的应用研究[D].上海:华东师范大学,2013.
[23]周欣,黄瑾,郭力平,等.我国学前儿童数学监测指标体系的构建[J].学前教育研究,2018(10):12-21.
[24]MILLS G E.教师行动研究指南[M].重庆:重庆大学出版社,2010(3):11-12.
[25]洪明.行动研究与幼儿教育[J].学前教育研究,2001(4):27-29.
[26]范晓文.让教师成为研究者:浅谈反思能力的培养[J].科学咨询(教育科研),2006(11):59.
[27]杨宏伟.幼儿教师怎样进行行动研究[J].教育与教学研究,2004(6):14-15.
[28]杨云秀.农村幼儿教师环境创设能力提升的行动研究[J].教育与教学研究,2014(6):124-128.
[29]席爱勇.数学多元表征:让概念形成过程“看得见”[J].教育研究与评论,2017(9):65-67.
[30]唐剑岚.国外关于数学学习中的多元外在表征的研究述评[J].数学教育学报,2008,17(1):30-34.
[31]黄瑾.论学前儿童数学学习中的多元表征[J].全球教育展望,2011(1):60-62.
[32]National Council of Teachers of Mathematics. Principles and standards for school mathematics[R]. Reston,VA:NCTM,2000:29.
[33]周晶.5~7岁儿童数学过程性能力构成要素探索与模型建构[J].学前教育研究,2018(2):12-24.
[34]NUNES T, BRYANT P, BARROS R, et al. The relative importance of two different mathematical abilities to mathematical achievement[J]. British Journal of Educational Psychology, 2011(82):136-156.
[35][38]MARIA A S, KONSTANTINOS Z. Building meaning through problem solving practices: the case of four-year olds[J]. The Journal of Mathematical Behavior, 2014,35:58-73.
[36]ZACHAROS K, KOUSTOURAKIS G. A critical approach to school mathematical knowledge: the case of realistic problems in Greek primary schooltextbooks for seven-year-old pupils[J]. Acta Didactica
Napocensia,2011,4(1):39-51.
[37]SHIAKALLI M A, ZACHAROS K. The contribution of external representations in pre-school mathematical problem solving[J]. International Journal of Early Years Education, 2012,20(4):315-331.
An Action Research on Promoting the Development of 5~6-year-old Childrens Pattern Ability Using Multi-dimensional Teaching Strategies
Yingchun Zhang,1 Juan Li,2,3 Tong Shen,4 Hongling Zheng,5 Lihong Wang,5 Ying Li5
(1College of Education and Art, Shangqiu Institute of Technology 476000 China; 2College of Teacher Education, Wenzhou University,Wenzhou 325035 China; 3Department of Education, Hebei University 071000 China; 4Beijing Normal University Kindergarten, Beijing 100875 China; 5Qingnian Lu Kindergarten, Baoding,071000 China)
Abstract: Pattern ability is an important mathematical ability in early childhood. It is an important prerequisite for children to form logical thinking, and it lays a good foundation for childrens future mathematics learning and development. This study adopted an action research paradigm, and used multi-representational teaching strategies to intervene in experimental classes of young children (30). The action research lasted for four months. The scope of intervention included group activities and regional activities. The researchers performed a group activity once a week, with four rounds of activity and a total of three rounds (12 collective activities). After one semester of intervention, we examined the childrens pattern ability before and after(60) to explore the influence of multi-representation teaching strategies on the development of childrens model ability, and analyze the effectiveness of multi-dimensional representation teaching strategies. The study found that: after the three rounds of action studies were completed, the childrens pattern ability improved both quantitatively and qualitatively. In terms of quantity, childrens pattern ability in the experimental class has improved significantly, both in comparisons of children before and after the test, or in comparison with the control class. In terms of quality, the children of the experimental class are more competent in the creation and transformation of the pattern, and they can apply the concept of the pattern to life; the teachers of the experimental class no longer “contradict” the multi-representation teaching strategy, and the ability has been improved. In addition, the study also discussed the reason of this action research why was effective, and we believed that reasonable programs and team members collaboration are key factors for effectiveness. Finally, we proposed educational advices: Help young children understand the relationship between mathematics and choose the appropriate way to represent; Pay attention to the cultivation of childrens multi-representation consciousness in daily life; Childrens process ability should get more attention in practice.
Key words: pattern ability, multi-representation, action research
