定态量子系统跃迁几率的微扰近似解与精确解对比研究①

齐若杉， 崔久波， 张海丰， 肖 逍， 赵 森， 庞福荣， 龚闻斌

(佳木斯大学理学院，黑龙江 佳木斯 154007)

0 引 言

量子力学是研究微观粒子的运动规律的重要物理学科，其主要研究对象是原子、分子、凝聚态物质、原子核和其他基本粒子的结构和物理化学性质[1～3]。根据量子理论，当被研究系统的能量取确定值时，系统处于定态；当系统的哈密顿算符显含时间时，研究系统的量子跃迁问题可以通过近似方法和精确求解的方法进行[4～6]。定态微扰理论就是有效的近似方法之一，在很多量子物理化学的研究中被广泛的应用[7～10]。本文就是基于定态微扰理论和精确解的方法求解定态量子系统跃迁几率。

1 含时微扰基本理论

考虑一个哈密顿算符为H0的物理系统，假定H0的本征值是非简并的分立谱，其本征方程可以表示为

H0|φn〉=En|φn〉

(1)

设H0与时间无关，但从t=0时刻开始，系统被加上了一个与时间有关的微扰项

H0(t)=H0+λW(t)

(2)

式中λ为参数，且λ≪1，W(t)是一个在t<0时为0的与H0同一数量级的算符。设系统的初态为H0对应于本征值Ei的本征态，则一阶近似下系统处在H0的另一个本征态|φf〉中的概率Pif(t)可以表示为

(3)

式中ωif=(Ei-Ef)/ћ为玻尔角频率，Wif(t)为W(t)的矩阵元，可以表示为

Wif(t)=〈φf|W(t)|φi〉

(4)

在常微扰的情况下，跃迁只能在能量相同的态之间发生，从|φi〉到|φf〉之间的跃迁概率Pif随时间线性增加，且有

(5)

式中ρ(Ef)是末态的态密度。

2 定态量子系统跃迁几率的近似解

假定一个量子系统有两个定态|1〉和|2〉，其能量本征值之差为E2-E1=ћω21。在t=0时系统处于状态|1〉，从此时开始加上一个与时间无关的微扰H′，其对应的矩阵元分别为

〈1|H′|1〉=0

(6a)

〈2|H′|1〉=ћω0

(6b)

〈2|H′|2〉=-ћω

(6c)

下边利用一阶含时微扰论，计算在t时刻系统处于|1〉态和|2〉态的概率。

应用一阶含时微扰论，可以计算P|1〉→|2〉，由于系统只有2个本征态，有

P|1〉→|1〉=1-P|1〉→|2〉

(7)

(8)

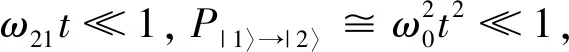
3 严格求解薛定谔方程

3.1 对角化哈密顿算符方法进行求解

首先，写出哈密顿算符H=H0+H′在本征态

|1〉和|2〉构成的基下的表达式

(9)

(10a)

(10b)

对于状态|ψ(t)〉可以得到

|ψ(t)〉=a1e-iλ1t/ћ|v1〉+a2e-iλ2t|v2〉

(11)

e-iE1t/ћ[cos(ω0t)|1〉-isin(ω0t)|2〉]

(12)

3.2 直接求解薛定谔方程方法

设|ψ(t)〉为

|ψ(t)〉=C1(t)e-iE1t/ћ|1〉+C2(t)e-iE2t/ћ|2〉

(13)

将(13)式代入一般形式的薛定谔方程

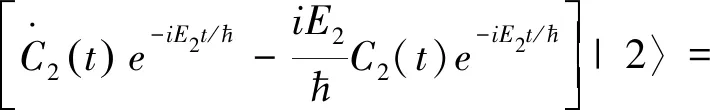
(H0+H′)[C1(t)e-iE1t/ћ|1〉+C2(t)e-iE2t/ћ|2〉]

(14)

用|1〉左乘(14)式得到

C1(t)e-iE1t/ћ(〈1|H0|1〉+〈1|H′|1〉)+

C2(t)e-iE2t/ћ(〈1|H0|2〉+〈1|H′|2〉)=

E1C1(t)e-iE1t/ћ+C2(t)ћω0e-iE2t/ћ

(15)

由此可导出

(16)

式中ω21=(E2-E1)/ћ。同样用|2〉左乘(14)式，可以得到

(17)

于是(16)和(17)构成一个系数C1(t)和C2(t)方程组

(18)

由第一个方程解出C2(t)并对时间微分可以得到

将(19)式代入第二个方程可以得到

(20)

利用初始条件C1(t=0)=0，由(20)式可以得到给出C1(t)=cos(ω0t)，并由此可以算出系数C2(t)=-isin(ω0t)eiω21t，于是最后得到

|ψ(t)〉=

e-iE1t/ћ[cos(ω0t)|1〉-isin(ω0t)|2〉]

(21)

可见两种方法得到的结果是一样的。

4 结 论

通过上边的讨论可以看出，系统处于状态|2〉中的概率为

P|1〉→|2〉=|〈2|ψ(t)〉|2=sin2(ω0t)

(22)