基于电阻率的砂土渗透系数测试方法
2019-08-08袁志华王炳辉王丽艳
袁志华, 王炳辉, 彭 超, 梅 岭, 王丽艳
(江苏科技大学土木工程与建筑学院, 江苏 镇江 212000)
渗透系数变化对土石坝渗漏、土体固结、边坡稳定性和液化等问题具有重要的影响[1-2], 但目前用于测试渗透系数变化的手段十分欠缺.Dewoolkar等[3]应用离心机研究蒸馏水饱和试样和羟丙基甲基纤维素饱和溶液试样, 发现高黏度孔隙液下超孔隙水压力产生更快, 而消散更慢; Wang等[4]用不同浓度聚合物溶液配置饱和土样,来增加孔隙夜的黏度,研究了渗透系数变化对试样液化的影响.这种通过改变孔隙液黏度的方法,虽然使试样的渗透系数发生变化, 但并不一定是土体本身渗透系数变化的真实反映, 所以急需一种可快速、准确、客观反映土体渗透系数变化的定量测试方法.电阻率作为土体固有的物性指标,很早就被用于土体性质的研究中.早在1942年, Archie[5]通过研究饱和纯净砂土的电阻率特性, 提出采用土结构因子的概念; Waxman等[6]考虑土颗粒表面所吸附的微粒导电性以及饱和度的影响, 给出了更全面的电阻率模型.随后电阻率测试在研究土性参数方面得到广泛应用, 高银灿等[7]等研究了粒径对饱和砂土电阻率特性的影响; Tang等[8]等提出冻土未固结含水量电阻率模型, 给出了土壤电阻率与冻土未冻结含水量的关系; Jinguuji等[9]则尝试采用电阻率法观察饱和砂土液化过程; 笔者[10]通过室内试验研究了孔隙水电阻率、砂土饱和度和孔隙率对电阻率的影响,并获得了饱和砂土电阻率与其孔隙率之间的关系.电阻率测试具有无损和快速的优点,并可通过预埋多组电极的方法,实现了对体积较大试样不同位置孔隙率及其结构等性质变化的实时检测.本文拟采用电阻率法,通过试验探讨渗透系数和结构因子等参数之间的定量关系,为实时分析土体结构的变化提供依据.
1 试验方案
1.1 试验装置和土样
试验主要设备为自制的动态电阻率采集仪和多功能测试装置, 盛放试样的装置为高度H=150 mm, 内径D=50 mm的空心圆柱体; 圆柱体顶部和底部预设有铜网电极, 侧壁从上到下等距设有3个测压管, 能同时测量电阻率和渗透系数.试验用水为自来水,土体为《GB/T 17671—1999水泥胶砂强度检验方法(ISO法)》中规格的标准砂, 先将砂洗净并烘干,再利用圆孔标准筛, 分别得到0.25~0.5, 0.5~1.0, 1.0~2.0, 2.0~3.0 mm共4个粒径区间以及两组粒径区间为0.25~3.0 mm、曲率系数Cc分别为0.91和0.64的混合粒径, 对应的工况组依次为D1~D6, 颗粒级配曲线如图1所示.

图1 各工况组用砂颗粒级配曲线Fig.1 Grain size curves for soils of experiments
1.2 测试原理
渗透系数测试方法[11]为KT=QL/(Aht),K20=KTηT/η20, 其中KT为水温T/℃时试样的渗透系数, cm·s-1;Q为ts内的渗透水量, cm3;L为两测压孔中心间的试样高度, cm;A为垂直于水流方向的截面积, cm2; 平均水位差h=(Dh1+Dh2)/2, cm,式中Dh1,Dh2为相邻测压管水头差;ηT为T/℃时水的动力黏滞系数, kPa·s, 可通过查表获得.在较小电流条件下,即使通电时间增加,极化吸收等通电历史的影响也极小[10], 变异系数CV=0.2%, 因此可以忽略.电阻率ρ=RS/L, 其中R为测试电阻,电极间的土体横截面面积S=19.63 cm2, 电极间距离L=15 cm.
1.3 试验步骤
本文试验共分6个工况组, 每个工况组分6个工况.制样采用“水中砂雨法”和微震密实法相结合的制样方法, 这种方法不需要重新装样, 能够确保同一工况组中的每个工况具有相近的结构性,使试验结果更贴近真实值.具体步骤: 每个工况组的第一个工况中,先称取质量为m0的干砂, 采用“砂雨法”在水中自然沉积, 并装满圆柱形装土容器, 称出剩余砂的质量m1, 则第一组试样的孔隙率n=ρs-(m0-m1)/V, 其中试样体积V=294.52 cm3, 砂颗粒的密度ρs=2.7 g·cm-3; 其余5个工况采用微震密实法制备, 以前一个工况的试样为基础, 采用透水石盖于试样顶部,通过轻微敲击装置底部,使试样振动密实,每次微震使试样产生的沉降量s控制在2~4 mm, 微震密实后的孔隙率计算中V=π(H-s)D2/4.表1为各工况试样的孔隙率.依据《GB/T 50123—1999 土工试验方法标准》规定的常水头方法测试试样的渗透系数, 并测量水温及试样和水的电阻率.

表1 各工况对应孔隙率Tab.1 Porosity for every samples of all working conditions
2 结果与分析
2.1 渗透系数和孔隙率的关系

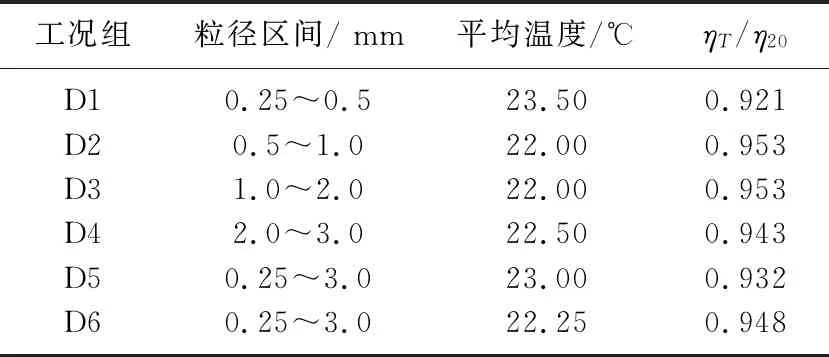
表2 各个工况组平均水温及ηT/η20Tab.2 Average water temperature and ηT/η20 of different working conditions
本文所得渗透系数和孔隙率之间的关系式与多孔介质渗透系数的理论Kozeny-Carman方程[12]非常相似, 两者较大差异在于参数C的影响因素, 本文试验结果表明其与均值粒径之间具有很好的线性正相关性, 而Kozeny-Carman方程则认为参数C与单位多孔介质体积的湿润面积、迂曲度等因素有关.由于湿润面积、迂曲度等都与多孔介质孔隙结构相关, 且迂曲度本身就有多种定义,使这些参数难以获得,因此本文方法更具有工程应用价值.
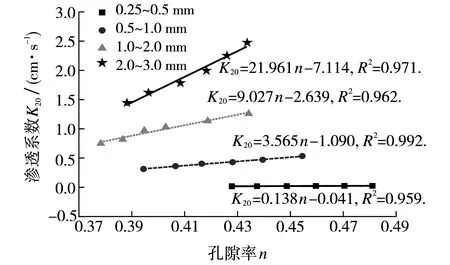
图2 渗透系数与孔隙率的关系Fig.2 Results of permeability coefficient for different porosity
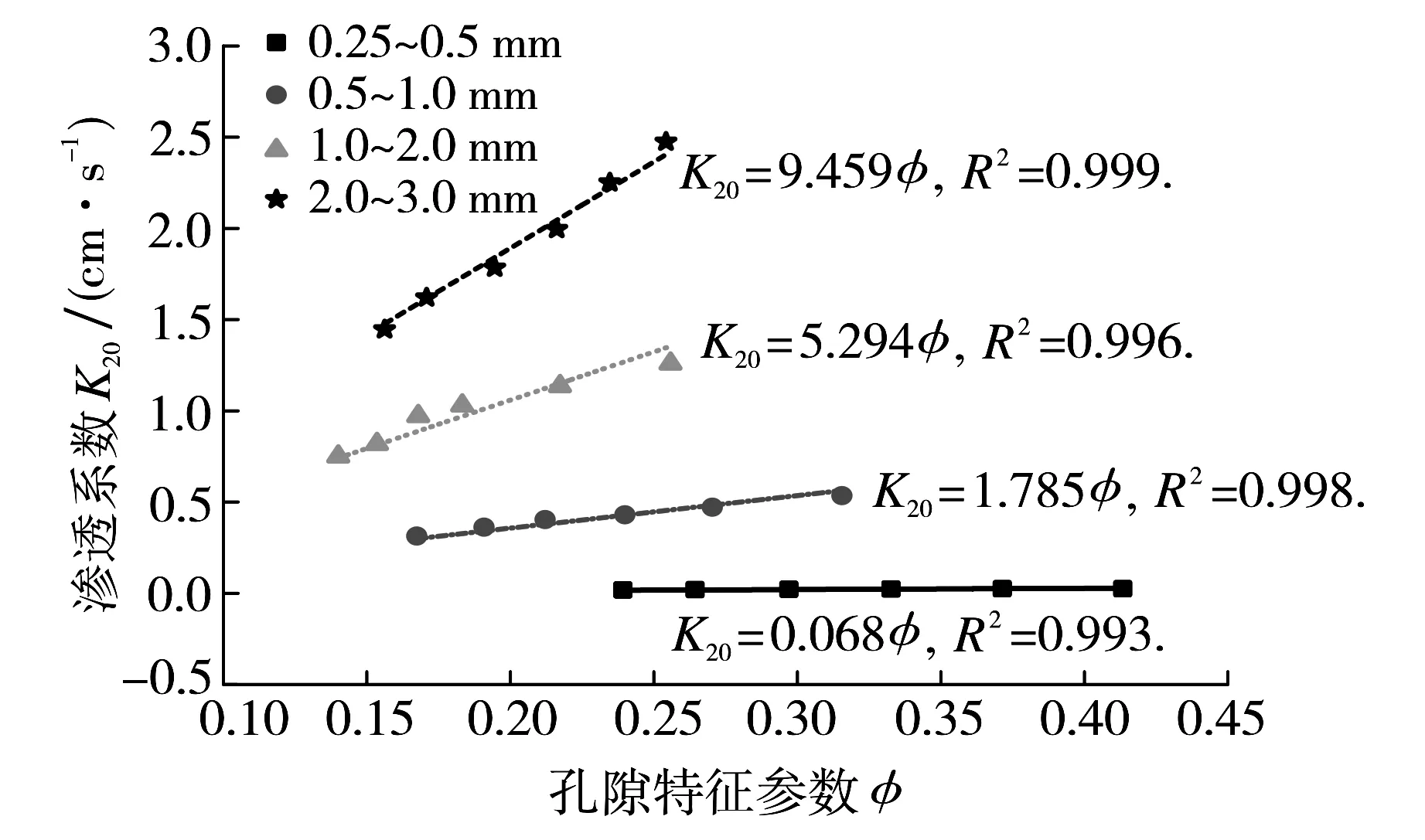
图3 渗透系数与孔隙率特征参数关系Fig.3 Relationship between permeability coefficient and porosity characteristic parameters

图4 形状参数C与均值粒径的关系Fig.4 Relationship between shape factor and average particle diameters

图5 渗透系数计算值与试验值的关系Fig.5 Relationship of permeability coefficient between calculated and measured values

表3 4个工况组试样的电阻率Tab.3 The resistivity of sample for four working conditions Ω·m
2.2 结构因子与孔隙率的关系
本文选用Archie[5]提出的电阻率模型, 土的电阻率ρ=aρwn-b, 其中ρw为孔隙水电阻率,a为土性参数,b为胶结系数.对于饱和纯净砂土试样主要通过孔隙水导电,由于本次试验的孔隙液为自来水,为了消除自来水和温度差异产生的影响, 采用结构因子F=ρ/ρw=an-b反映试样的孔隙特征,故只要测得饱和试样的电阻率和对应孔隙液的电阻率, 就能获得反映试样孔隙特征的结构因子.表3为各工况试样的电阻率, 图6为4个工况组结构因子与孔隙率的关系图.从图6可以看出, 孔隙率越大,结构因子越小,颗粒特征的影响可以忽略, 拟合可得F=1.106n-1.412,幂指数值1.412在1.3~2.0之间.
2.3 渗透系数与结构因子的关系
图7给出了不同工况渗透系数与结构因子的关系.从图7可以看出,相同粒径区间的渗透系数随结构因子增大而减小.渗透系数和结构因子的大小取决于该孔隙率下砂颗粒形成的孔隙结构,对于同一个试样可以认为流场中和电场中的孔隙结构相同,因此可以通过电阻率测试获得饱和试样的孔隙结构,进而可以预测该试样的渗透系数, 为了进一步研究渗透系数和结构因子的定量关系,将公式K′=K/C归一化处理,消除颗粒粒径的影响,C取试验数据的拟合结果, 得到归一化的渗透系数与结构因子的关系如图8所示, 则结构因子修正为F′=(a/F)3/b[1-(a/F)1/b]-2, 其中a,b分别取1.106和1.412.图9为归一化的渗透系数与修正结构因子的关系.结果显示,渗透系数和修正结构因子的定量关系为K=CF′, 通过结构因子换算得到的渗透系数与测试结果十分相近,可通过此式实现电阻率对土体渗透系数的测定.

图6 结构因子与孔隙率的关系Fig.6 Relationship between formation factor and porosity

图7 渗透系数和结构因子关系Fig.7 Results of permeability coefficient and formation factor
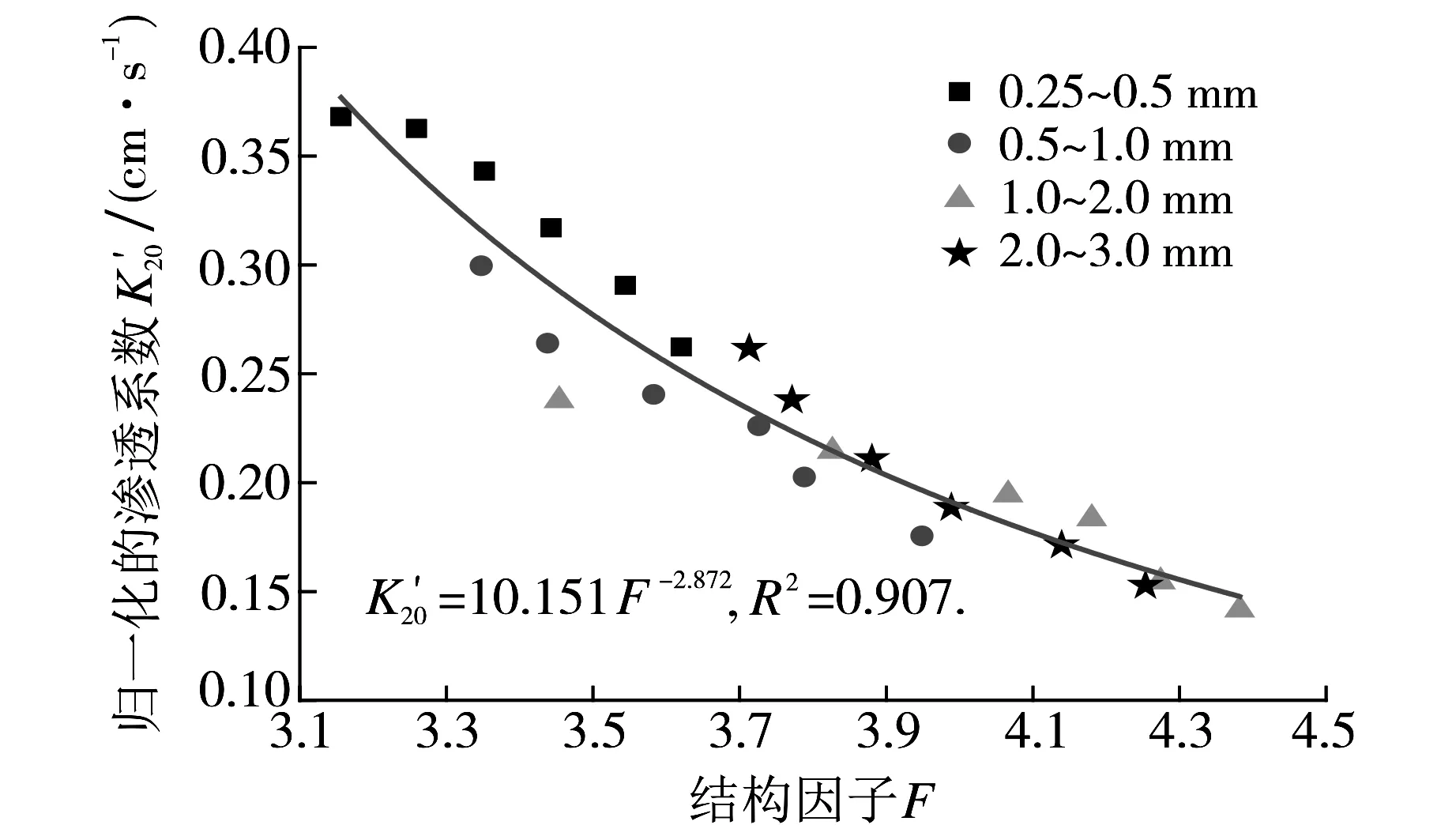
图8 归一化渗透系数和结构因子的关系Fig.8 Relationship between the normalized permeability coefficient and formation factor

图9 归一化渗透系数与修正结构因子的关系Fig.9 Relationship between the normalized permeability coefficient and the modified formation factor
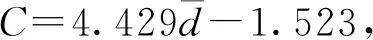
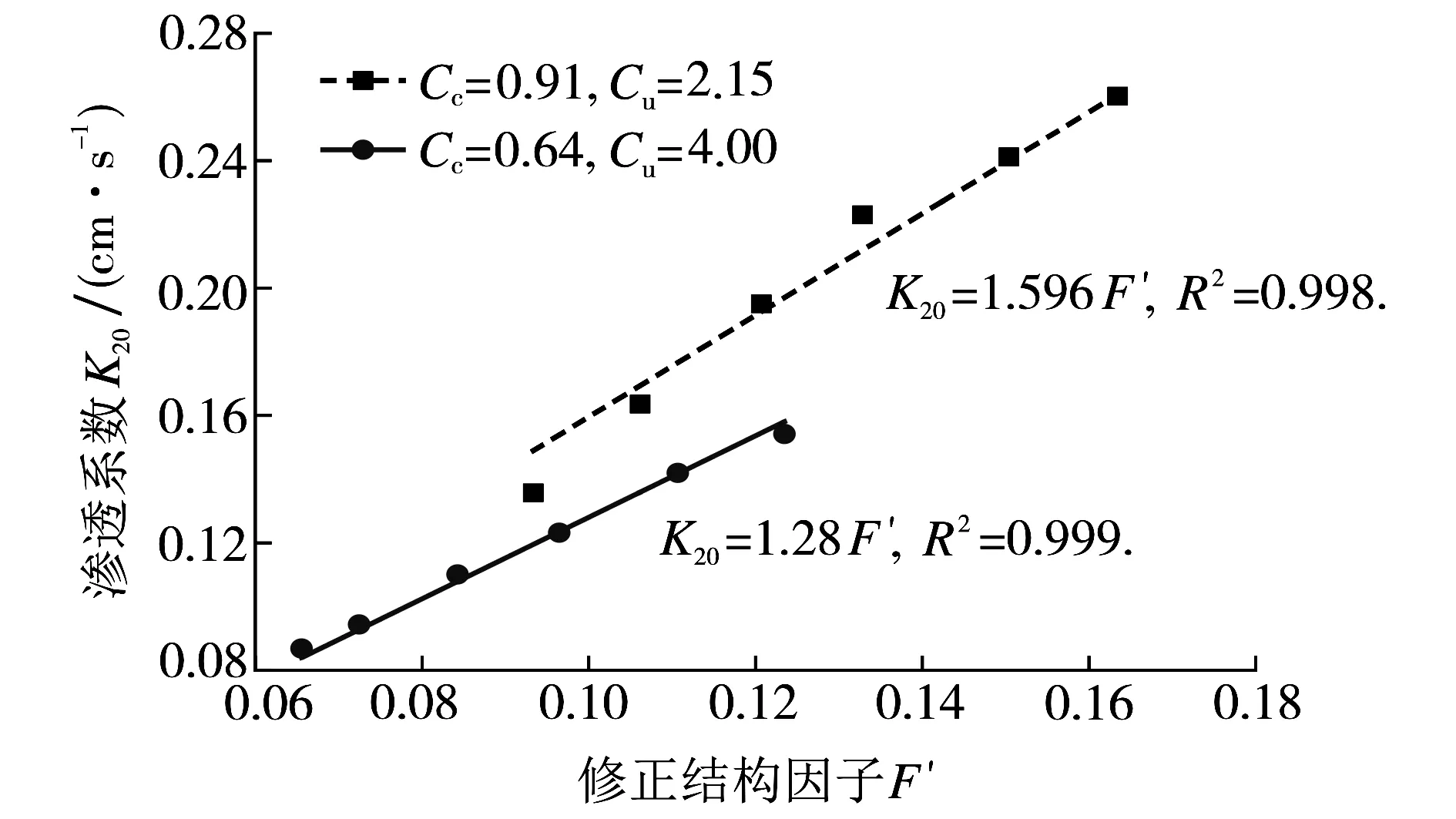
图10 混合粒径渗透系数和修正结构因子的关系Fig.10 Relationship between the permeability coefficient and the modified formation factor for mixed sand sizes
3 结论
1) 相同粒径区间孔隙率越大,渗透系数越大, 孔隙特征参数φ与渗透系数具有很好的正比例关系;相近(相同)孔隙率下,均值粒径越大,渗透系数越大; 孔隙率变化相同时,均值粒径越大,渗透系数变化越快.
2) 饱和纯净砂的结构因子与孔隙率成较好的负幂指数关系.
3) 渗透系数K随结构因子F的增大而减小,且K=CF′.
4) 结构因子换算得到的渗透系数与常水头测试得到的渗透系数十分吻合, 证明可以通过电阻率测试来获得土体的渗透系数,考虑到电阻率无损和动态采集的特点,本文获得的渗透系数与结构因子的关系,为电阻率测试应用到有关渗透系数变化的研究奠定基础.
