一类流行性出血热模型的全局稳定性

李 凤, 刘俊利

(西安工程大学理学院, 西安 710048)

传染病动力学模型可用于显示疾病的发展过程, 揭示其流行规律, 预测其变化发展趋势, 分析疾病流行的原因和关键因素,寻求对其预防和控制的最优化策略, 为人们防治决策提供理论基础和数值依据[1-2]．流行性出血热, 又称肾综合征出血热,是由汉坦病毒引起并经鼠传播的自然疫源性疾病,潜伏期为4～46 d, 平均约为2周[3-4]．人可通过自然感染获得动态的免疫屏障, 使感染过流行性出血热的人不会再次感染[5]．目前, 对出血热的研究主要集中在疫苗研制和病毒分离提取等[6]．本文拟利用常微分方程建立出血热传染病模型, 并通过理论分析, 探讨出血热传染病的动力学行为, 为疾病的预防及控制提供理论依据．

1 数学模型

根据流行性出血热的状态转移情况, 并综合考虑流行性出血热的传播途径和病理原理, 参考文献[7-8]建立模型

(1)

其中SH,EH,IH,RH分别表示t时刻人群中的易感人数、潜伏人数、染病人数、恢复人数;SM,IM分别表示t时刻鼠群中的易感数和染病数;x表示已具有传染性的出血热病毒数;A1,A2分别代表人和鼠的输入率;β1,β2分别表示人群和鼠群中易感者被感染的比例系数; 1/σ表示出血热病毒在人体内的平均潜伏期;γ表示人被感染后的恢复率系数;a表示染病鼠的释放率;d表示出血热病毒离开病鼠后消亡率系数;d1,d2分别表示人和鼠的死亡率系数．设t时刻总人数N=SH+EH+IH+RH．

2 模型的基本性质

2.1 正性及有界性

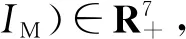
定理1a) 模型(1)满足初始条件的解满足: ∀t>0,SH,EH(t),IH(t),RH(t),x(t),SM(t),IM(t)均为正数; b) 当t→0时,模型(1)满足初始条件的解最终进入区域Γε．

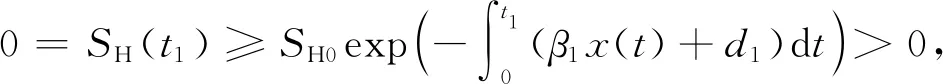
有界性: 由模型(1)得dN/dt=A1-d1N, 则limt→∞N=A1/d1, 故∀ε>0, 当t>t2>0时, 有N≤A1/d1+ε．同时d(SM(t)+IM(t))/dt=A2-d2(SM(t)+IM(t)), 有limt→∞(SM(t)+IM(t))=A2/d2, 故∀ε>0, 当t>t3>0时, 有SM(t)+IM(t)≤A2/d2+ε, 则dx(t)/dt=aIM(t)-dx(t)≤a(A2/d2+ε)-dx(t)．由比较原理知, 当t>t4>0时, 有x(t)≤ad-1(A2/d2+ε)+ε=aA2/(dd2)+(a/d+1)ε．令t*=max{t2,t3,t4}, 则∀t>t*, 结论成立．

注1根据定理1,当t充分大时,模型(1) 的所有正解进入或停留在区域Γε中; 因此,在本文中,仅考虑区域Γε中模型(1)的动力学行为．

2.2 基本再生数和平衡点的存在性

3 平衡点的稳定性

定理2如果R0<1, 则无病平衡点E0是全局渐近稳定的; 如果R0>1,则E0不稳定．

证明 模型(1) 在E0处的雅可比矩阵为

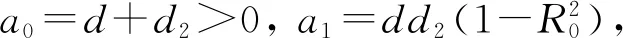
首先考虑方程

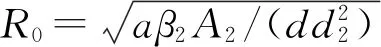
定理3如果R0>1, 则地方病平衡点E*局部渐近稳定．

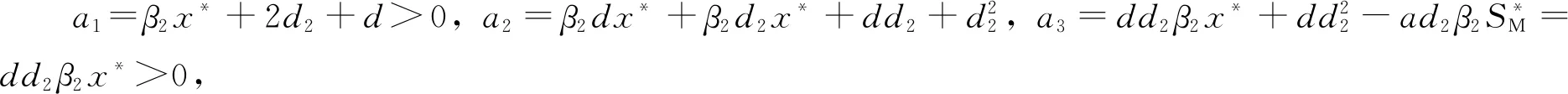
定理4如果R0>1, 模型(1)地方病平衡点E*全局渐近稳定．

证明 因t→∞时,N→A1/d1,SM+IM→A2/d2, 则模型(1)退化为

(2)

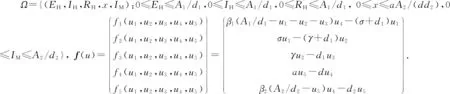
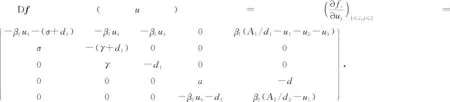
显然Df(u)是非约化的, 因为

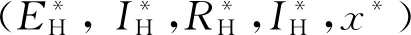
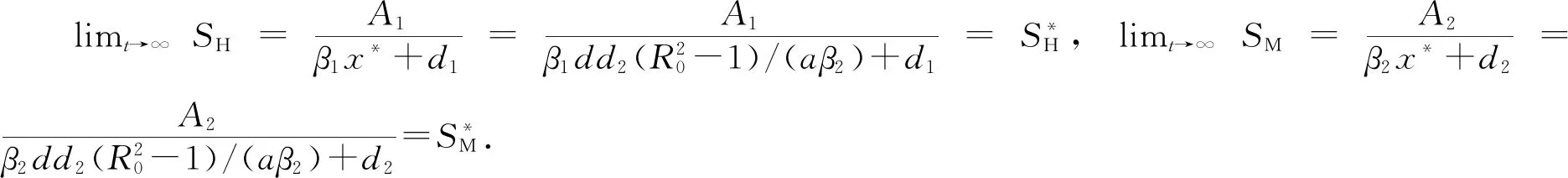
4 结语

本文建立了一类出血热传染病的模型, 计算了模型的基本再生数R0, 并发现R0完全决定模型的动力学行为: 当R0<1时,出血热无病平衡点全局渐近稳定;当R0>1时,出血热无病平衡点不稳定,存在唯一的地方病平衡点,且该平衡点全局渐近稳定,说明在人群中出血热传播状况会一直持续．结果表明, 染病老鼠的释放率a越小,老鼠的输入率A2越小,出血热的传染人数越少,说明防鼠、灭鼠是预防出血热的重要举措, 同时要注意个人卫生,对预防和控制出血热感染也是十分有必要的．